谈数学教学情境设计的四对关系
张亚楠 方均斌 翟金鑫
(温州大学 325035)
数学情境教学设计意在让学生能够产生“设身处地”的情境效应,力图使学生能够有效调动各个感官参与数学思维活动,而情境教学的推行丰富了数学教学的形式,使数学教学效果得到了一定的提升.然而,实践证明,情境教学如果没有处理好一些关系,很可能会造成一些负面效应,使得教学效果大打折扣.我们认为,数学教学情境设计必须处理好以下四对关系,使得教学效果更为理想.
1 倾实性与可隔性
根据我国目前的教学现状,学生学习数学基本上都是在教室内完成的.在这个“教学基本空间”——教室里,充满着与基础教育阶段的数学知识有着千丝万缕联系的情境,我们应设身处地让学生观察身边的世界而不必舍近求远地追求“创设情境”,因为情境教学更多的是倾向于学习者主体的切身体验(简称感知的倾实性),但情境的创设则因各种原因,往往允许与学习者存在一定的距离(简称情境的可隔性),因此,必须因地制宜,灵活掌握.
例1教学比赛中的“矩形”教学设计
2012年某地举行了省级数学教学比赛,其中的一个课时是《矩形》,组织者采取“同课异构”的手段让教师进行观摩.就三个示范教学的教案来看:(1)教师甲的情境创设是这样的:“如图(显示图形),在6根木棒中选取其中4根,搭出一个平行四边形.”他只是让学生观摩PPT上的图像作为情境;(2)教师乙先播放一段“伸缩门的移动”视频,然后用flash展示平行四边形的形状随其中一个角的度数的变化而变化的过程,从一般形式转变为一个角为直角时的特殊形式.(3)教师丙设置了一个情境:“初二学生在学农学工劳动中,看到师傅这样做一个平行四边形的铝合金窗框,一边放在地上(用投影屏幕显示图形),问学生:‘为了让这个铝合金窗框稳定一些,他会怎么做呢?’”
这三位教师都利用了图片、视频、动画等方式设置了矩形的情境,图文并茂,形象直观.然而,我们在疑惑:“整个教室充满着‘矩形’,为什么会视而不见呢?”学生面对播放多媒体的屏幕、黑板、门窗、教室的墙面、地面、桌面、书本、讲台等等,为什么我们要舍近求远去创设所谓的“情境”?学生将来走向社会接触最多的是周围的世界,让他们能够“触景生情”地采取用数学的眼光观察周围世界,应该是我们设置情境教学的重要目的之一,这些舍近求远的做法可能违背我们情境教学的初衷.其实,针对矩形的情境引入,教师只要问学生:“前面我们学习过平行四边形,大家思考(观察)一下,生活中哪些地方用到了平行四边形?用得最多的平行四边形是什么形状的?”这样的情境设置既真实又不用花太多的精力去制作所谓的多媒体课件,何乐而不为?
在基础教育阶段,很多数学模型都可以在学生的生活(尤其要关注教室这个空间)中找到,条件允许的话,教师可适当携带一些教学道具,尽量让这些情境教学真实而亲切,充满真实感.
我们指出前面三位教师的设计没有关注周围的环境,并不是出于指责,而是提醒大家对周围的真实世界要尽量引导学生进行观察,“警示”大家不要舍近求远.当然,一些人为创设的情境只要恰当地引用也会让学生 “别有一番滋味”.故在这里我们提出要正确处理好学生学习感知的倾实性与数学情境的可隔性之关系,即,处理好“远”与“近”的关系:一是针对学生生活“空间”或“时间”以及兴趣爱好,在可能的情况下尽量贴近学生;二是针对学生敏感性较强的“心理空间”和“生理空间”,教师要谨慎对待,有时甚至要“舍近求远”(例如,在讲解排列组合的时候,针对青春期的学生,同学之间“配对”情境就要避免);三是不走极端,必要的时候要“远近结合”,只要让学生产生“此境生好情”或“由情促探境”即可.
2 求实性与可虚性
在教育过程中,我们往往要求数学教学与实际情况相吻合(即教育要求具有求实性),而一些数学情境在创设的时候往往允许虚构(可虚性).这种“实”与“虚”的关系源于数学与实际之间的关系,从某个角度上讲,数学是研究现实世界的空间形式与数量关系的一门科学,但它不是现实世界的简单“境面反射”,而是经过人们抽象思考后的产物.这种抽象过程必须正确处理“虚”与“实”的关系,如果处理不好,很可能会面临着“错”与“对”的问题.
例2一元一次方程的应用教学设计[1]
这是浙教版教材七年级上册 “5.3:一元一次方程的应用”创设的一个“2002年釜山亚运会的情境”,甲说:“2002年釜山亚运会上,我国获得150枚金牌,比1994年亚运会我国获得的金牌数的2倍少38枚.”乙在思考:“1994年亚运会我国获得几枚金牌?”其实,这里面数据有误(1994年亚运会我国获得125块金牌,1986年才是94块[2]).
就数学而言,情境设计是为了让学生建立具体的数学模型去解决实际问题,只要不影响建模的过程,一般人是不太会怀疑数据来源的真实性.这就给我们提出一个警示:提供原始的数据必须真实可靠!否则,经过第二道程序——数学建模处理后的结论很可能会在具体应用过程中产生误导甚至产生不良的后果!
对于基础教育阶段的学生,他们对数学情境的要求往往只是在具体的情境中学会如何建立数学模型以及由这个模型产生数学结论,还很少触及真正的实际应用,只要这个过程不要对学生产生误导即可.例如,一道经典的数学名题——“鸡兔同笼”,这样的情境是否真实无从考究,但不影响这是一道“数学名题”,即便有人讽刺:“只要对着笼子数一下,何必动脑筋?!学数学的人真傻!”其实,这道题的真正价值在于人们的数学思考过程及其数学模型,至于情境是否真实无关重要.
关于数学情境的“虚”与“实”,我们的理解是:(1)要看数学情境的创设意图.如果只是对学生进行数学建模训练,适度的虚拟是可以的.而如果需要解决实际问题,数据应该真实,不打马虎眼;(2)数学情境创设,还兼顾着人文教育的目的,不能对学生的教育产生负面效应甚至是误导.例如,我们上面所举的例子,如果让学生误知我国在亚运会上的金牌数,绝对是对学生不负责的做法,另外,出现了一些诸如“年龄失真”[3]、“浓度失实”[4]等“低级错误”也会让学生对数学的良好印象打折;(3)对学生所感兴趣的话题尽量让学生有真实感.但对虚拟的情境我们也不应排斥;(4)要关注“虚”“实”之间的合理运用.例如,对于具备“实境”条件的问题,可以先用“虚境”提高学生的想象力,然后再“务实”.而无法做到“实境”的数学情境问题,有时未必一定要“务实”,适度“务虚”也是可以的,关键是要看学生情况及教学意图.
3 完善性与游散性
学生学习就是为了追求认知上的完善,即达到“认知的完善性”.完善的认知需要依据知识内在的逻辑系统,然而,现实情境之间却不一定有如此严谨的相关性,它们具有一定的游散性.情境的游散性与认知的完善性之关系我们称之为“情”与“理”的关系.“情”指数学情境,而“理”是“理由”,探求数学问题产生的“理由”是数学教学的重要任务,也是学生认知完善的需要.时下,数学情境教学“风靡全球”,我国似乎也不例外,这与我国以往教材过于强调知识间逻辑关系有很大的不同.学生将来走向社会,会遇到各种各样离散的情境,如果能够形成“用数学的眼光看世界”的意识,数学学科的一个很重要的“教学目标”也就实现了.于是,我们老师频繁地在课堂教学设计中设置情境,以提高学生捕捉数学信息的敏感性,这叫“频繁‘触景’,意在 ‘生情’”.但是,我们不能忘记学生在学习阶段,所学的知识如果缺乏逻辑链,是不利于他们形成完善的数学认知结构的.所以,我们在给学生设置数学情境的时候,其背后应该有一条数学思想方法的支撑主线,在适当的时候让学生感悟到这种“背后语言”,达到“动之以‘情’,晓之以‘理’”之境界.
例3函数单调性、奇偶性的情境设计
函数单调性、奇偶性的教学设计一直是我们数学教师讨论的一个热门话题,经常在教学设计、说课、上课比赛或教学观摩中频繁出现.就函数单调性而言,通常都是设置一个函数实际问题(诸如气温随时间变化曲线),让学生观察函数的变化规律,然后指出函数单调性的直观概念,进一步再抽象出单调性的抽象定义,在函数奇偶性的教学设计中也基本如此.这种设计我们认为很不错,但如果能够加上一个数学思想方法的“逻辑链设计”就更好了,也就是说,学完这两个性质后,教师对学生说:“研究函数就是研究函数的两个变量之间的关系,核心的一个字:‘变’,即:当一个变量变化时,另一个变量是如何变化的?而变量变化经常是‘变大’、‘变小’及‘变号’.”简言之,即“一个变量大小变化,另一个是否与之同步?”“当一个变量变号(即变成它的相反数),那么另一个是否也跟着变号(即变成自己的相反数)?”这样,就把函数单调性、奇偶性牢牢地“链”在学生的“认知结构”上.
现实生活情境的随机性强,而学生学习数学则往往追求“前因后果”,探求其“理由”.“情”的“随机性”与“理”的“确定性”是我们在数学情境教学过程中应该正确处理好的关系,数学情境教学尽量不要让学生“不识庐山真面目,只缘身在此山中”,而应该让他们对背后的数学思想有所感悟.为此,我们提这样的几点教学建议:(1)遇“情”思“理”.其意有二:一是教师对实际情境,要引导学生学会用数学去探求“理由”或形成新的数学问题;二是引导学生进行必要的感悟:“今天老师为什么对这个问题感兴趣?”体会背后的数学思想方法.(2)由“理”探“情”:形成用“数学知识”去寻求“实际应用”的“应用意识”.会用所学数学去解决实际问题,鼓励学生在学习数学的时候多思考:“所学数学在实际中有什么用?”“在什么场合下有用?”“是直接用还是间接地用?”等.(3)“情”“理”结合:关注“生活的游散情境”与“数学的严谨结构”的有机结合.让学生对数学情境和数学原理形成一种不断反思的交互意识;有时某些“情”也能够助“理”,即某些生活情境能够帮助学生有效地进行数学思考.比如,两杯不同浓度的咖啡混合,根据生活常识就可以知道混合后的浓度就介于二者之间.于是我们就可以得到不等式:
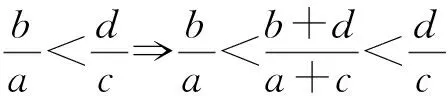
此外,在现实生活中,很多情境可能“一闪即逝”,如果没有一定的“珍惜追求”意识,一些数学发现就这样错过了.例如,欧拉就根据“七桥问题”的现实情境开创了“拓扑学”,而很多人却与之“失之交臂”!所以,在学生时代,情境教学就需要培养学生“见‘情’惜‘理’”的意识.显然,外界引导的有效性在学生对现实情境的好奇心、兴趣、注意的持续性等方面的体验起着关键的作用,尽管我们以前也有一些学者涉猎,但我们认为还存在很多的话题值得大家进一步的研究.
4 择取性与全息性
实际情境往往具有整体的性质,但教师在具体教学的时候,往往有选择地选取其中部分进行“加工”,相对于整个实际情境而言,教师的选择就显得有些零散.这有点像我们小时候读过的寓言《瞎子摸象》——各执一词,学科分类式的培养也势必导致择取性处理现实情境的教学举措,但全息性的“综合过程”却疏于理会!
例4第二十四届国际数学家大会会标

针对浙江一带的学生,他们在初中教材[5]中学习勾股定理的时候,就遇到这个标志,在高中学习基本不等式的时候也遇到这个标志[6].以同样的一个会标作为情境,初中教师与高中教师各取所需地分别“得到”勾股定理和基本不等式.这个例子说明,同一个数学情境,由于教师的教学意图不同所得到的数学结论也有方向上的差异.另外,遇到这个图标,美术教师很可能会考虑色彩的问题;政治和历史教师则会考虑爱国主义教育问题;语文教师则会写一首赞美的诗歌;物理老师则会考虑会徽架子的受力情况;……,这种教学现象应该属于必然和正常的.但我们在思考:针对一个具有完整信息的实际情境,在教学设计的时候如何正确处理情境的全息性与教学的择取性,即“整”(全息性)与“零”(择取性)的关系?我们的想法是:(1)要先“整”后“零”:引导学生经历“综合情境”的“多向讨论”,即在引导之前给学生一个讨论的机会,让他们进行思维发散与“优化”[7],此时教师不宜过多干涉;(2)要多向生“零”:对学生所得到的结论不宜采取“为我所用”的“急功近利”做法,应该允许学生“不按老师的套路走”,然后客观地进行必要的评价和引导,可以采取“同学们的想法大部分都很不错!但假如……,我们应该如何处理?”“……同学的想法也很不错!这个内容我们后面会涉及,如果大家对这个想法感兴趣,我建议…….”等诸如此类的语言;(3)要集“零”窥“整”:即使学生根据教师所创设的实际情境,采取与教师意图几乎一致的想法,但教师有时还得“无事生非”:“假如这个问题从另一个角度去看……,你会怎么处理?”从“多向的思考”中把握“整体的数学命脉”,促使学生数学视野的开阔:既见森林,又见树木!
捷克教育家夸美纽斯在《大教学论》中指出:一切知识都是从感官开始的.他指出情境教学的核心是创设生动具体的情境,引起学生的情感体验,以此推动学生认知活动的进行.我们所提的“四对关系的处理”就在于教师需要更好地体现情境教学的本质特征,使得数学情境教学显得自然而又体现数学学科的特点.

