组内相关系数的理论基础及建模应用

乔 舰

(中国矿业大学(北京) 理学院，北京 100083)



【统计理论与方法】

组内相关系数的理论基础及建模应用

乔 舰

(中国矿业大学(北京) 理学院，北京 100083)

对用于测度数据可靠性的统计指标组内相关系数进行了理论基础论证、建模步骤分析、软件实现说明和实际数据统计分析；对组内相关系数建模中涉及的方差分析模型选择、相对一致性和绝对一致性区分、分析结果解释等都进行了详细说明。

组内相关系数；随机效应模型；混合效应模型

一、引 言

实证分析中，观测数据不可避免地存在测量误差，进而对统计分析过程及结果解释会产生严重影响，可通过对观测数据一致性或可靠性的度量来衡量误差造成的影响程度。组内相关系数(intraclass correlation coefficient，简记ICC)就是为完成该任务而构造的，其定义为组间方差与总方差的比值，用于对相同研究对象多次观测数据的一致性或可靠性的度量，既可用于如计数、比例等定量数据，也可用于如类别等定性数据。它对于心理学、教育学、流行病学及社会学等领域的实证研究至关重要。

ICC取值越接近1，说明对相同研究对象的多次观测数据之间越接近，观测结果越可靠；取值越接近于0，说明多次观测数据之间差异越大，观测结果可信程度越低；若取值负值说明测量过程本身存在着系统偏差。已被普遍接受的ICC评价标准是：当取值小于0.4时，观测数据可信程度较差；在0.4～0.59之间时，可靠程度一般；在0.6～0.74之间时，一致性较好；取值大于0.75时，观测结果值得信赖[1]。

观测数据的一致性可区分为绝对一致性和相对一致性[2]。所谓绝对一致性是指对相同研究对象多次观测数据数值上的接近程度；相对一致性是指对相同研究对象多次观测数据趋势上的相近程度。例如在研究生入学复试时，假设每位考生要接受5位考官的测试评分(百分制)，测试过程先笔试后面试，且规定笔试成绩低于60分者不得录取，面试成绩排名前75%者录取。若5位考官中有1位比较苛刻，给所有考生的评分都比较低；1位考官比较宽松，给所有考生的评分都比较高，则此过程中评分的绝对一致性会影响考生笔试成绩，相对一致性会影响考生的面试成绩。本质上绝对一致性与相对一致性测度是同一个问题的两个方面，是两个没有任何关联的不同概念。在定义和估算ICC时应对二者进行区分，切不可将ICC如其名称一样，简单理解为观测数据之间的相关性。

二、组内相关系数的理论基础

ICC的定义和估计都是基于均衡数据方差分析模型的均方误差进行，此处数据的均衡指的是每位评定者对每个观测对象都需且仅需评分1次。已有文献给出了在均衡数据单因素随机效应、两因素随机效应、两因素混合效应模型下ICC的定义、估计量、置信区间、假设检验等结论[2]。本文将给出相关模型的统计学理论基础。首先需要指出的是，当数据均衡时，方差分析中有关总误差的平方和分解是成立的，且分解后的各平方和之间是相互独立的。假定由观测对象构成的总体中随机抽取了n个观测对象，且每个观测对象都由k位评定者独立评分，记yij为第j位评定者对第i个观测对象的评分，i=1,2,…,n;j=1,2,…,k，那么有如下3种情形：

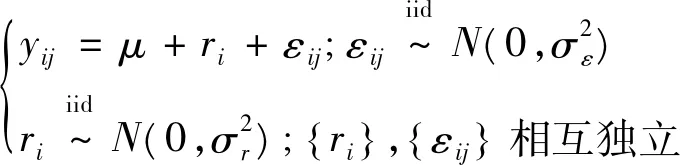
且SSE、SSR相互独立。

情形2：均衡数据两因素随机效应模型

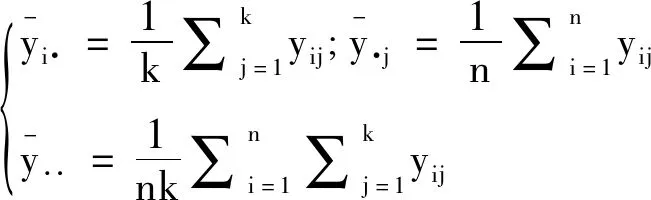
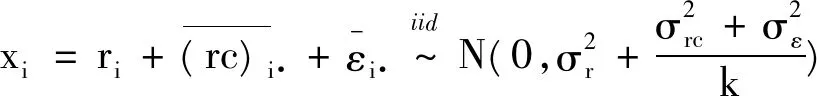
情形3：依据方差分析模型的分类，两因素混合效应模型又分为无限制混合效应模型和有限制混合效应模型。已有文献分别对无限制混合效应模型和有限制混合效应下的ICC的定义和估计进行了研究，但算法实现多以有限制混合效应模型为研究对象[2-4]。

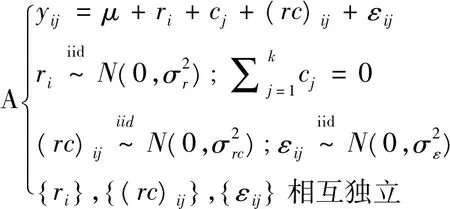
上述三类方差分析模型的理论性质是ICC的估计量、置信区间、检验统计量分布的统计学基础。需要说明的是，鉴于不含交互效应的两因素方差分析模型是本文给出相应模型的特例，故本文未阐述其理论基础。

三、组内相关系数的统计建模

ICC的统计建模需遵循如下的规则与步骤[5-6]。

第一步：确定是在单因素方差分析模型还是两因素方差分析模型中估算ICC，这取决于试验中评定者的选取方式。若每个观测对象面对的评定者都不相同，每位评定者是从评定者们构成的总体中随机抽取得到，即试验仅对观测对象间的差异感兴趣，则选择单因素方差分析模型，该模型中观测对象是唯一随机效应，不存在评定者效应；若每个观测对象面对的评定者相同，这些评定者是从评定者们构成的总体中随机抽取得到，且分析结果要推广到这些评定者们所在的总体，则选择两因素随机效应模型，该模型中观测对象、评定者及二者之间可能存在的交互效应都是随机效应；若每个观测对象面对的评定者相同，这些评定者就是所有的评定者，且分析结果也仅限于参与该试验的评定者内部交流，则选择两因素混合效应模型，该模型中评定者效应为固定效应，观测对象及观测对象与评定者之间可能存在的交互效应是随机效应。

第二步：确定分析估算ICC的单位，即是测量单个评分之间的一致性还是测度多个评分的均值之间的可靠性，这取决于试验设计本身。一般而言，单个评分之间的ICC比较常用；若单个评分不可信或评定者组队评分时，评分均值之间的ICC才起作用。一般而言，评分均值之间的一致性会高于单个评分之间的一致性，且随着评分均值中评定者个数的增加，ICC估值会提高，Bliese给出了要使该估值达到指定水平的最低评定者个数计算公式[5]；Shrout和Fleiss给出了评分均值ICC估算中涉及到的合理评定者个数问题说明和计算方法[5]。当基于两种估算单位得到的ICC结果相差较大时，研究报告应将两者都给出，以展示二者之间的差异[5]。

第三步：确定ICC测量对象是绝对一致性还是相对一致性，这取决于试验设计的目的。事实上两者的本质区别在于ICC分式定义表达式的分母，试验中评定者的系统误差对相对一致性的测量无影响，但对绝对一致性的测量却有着直接的影响，进而评定者的方差在绝对一致性ICC定义的分母中存在，在相对一致性ICC定义的分母中不存在，从而在进行观测数据可靠性度量时，若考虑评定者效应则为绝对一致性ICC，若不考虑则为相对一致性ICC。单因素方差分析模型本身未考虑评定者的影响因素，进而测度的是相对一致性ICC；两因素方差分析模型中测度ICC时，需根据试验设计目的确定相应测度对象。

四、组内相关系数的软件实现

包括SAS、SPSS在内的众多统计软件都可实现ICC的估算，但都稍显复杂[6-7]。事实上基于软件包irr的R软件可以轻松实现文献所涉及有关ICC的所有统计分析过程[2]。

软件包irr中用于ICC计算的命令为：

icc(data, model = c("o", "t"),type =

c("c", "a"),unit=c("s", "a"), r0 = 0, conf.level=0.95)

其中data为待分析数据集，行代表研究对象，列代表评定者；若数据出现删失，则整行数据从数据集中移除。model为估算ICC的模型，o代表单因素方差分析模型(默认选项)，t代表两因素方差分析模型。type为ICC测度对象，c代表相对一致性(默认选项)，a代表绝对一致性，单因素方差分析模型之下只能选择c；unit为ICC估算单位，s代表单个评定者(默认选项)，a代表多个评定者均值；r0为有关ICC的单侧假设检验H1:r>r0中的假定的ICC真值(默认值为0)；conf.level为有关ICC真值置信区间的置信水平(默认值为0.95)。该命令将一次给出文献所涉及的所有统计分析结果[2]。

在此软件实现过程中有几点需要说明：

1.基于两因素方差分析模型的ICC，在随机效应和混合效应模型的不同情形下和在交互效应存在与否的不同情形下的定义和解释都不同，但其估计量是相同的，进而在R软件的算法实现中未加区分，使用者应充分认识到不同情形下ICC的不同，尤其在结果解释上的不同，见表1。由于每位评定者对每个观测对象只评分一次，故用于测定ICC的两因素方差分析模型中，尽管观测对象和评定者间的交互效应可能存在，但不可单独检验其是否存在或估算其值，进一步含有观测对象和评定者交互效应的两因素混合效应模型是无法进行ICC估算的，无论是绝对一致性ICC还是相对一致性ICC，已有文献对此进行了理论说明[2]。

表1 两因素方差分析模型中ICC的解释

3.一般而言，对于相同数据的基于单因素方差分析模型得到的ICC估值应小于基于两因素方差分析模型得到的结果，无论相对于单个评分还是评分均值。

五、组内相关系数的数据分析

表2为4位考官对6个应试者整体素质的评分情况(10分制)。为测度该评分的一致性或可靠性，现进行基于ICC的统计分析。表3为基于R软件命令icc得到的结果，其中估计量ICC(u,v,w)中u代表单因素模型(o)还是两因素模型(t)；v代表绝对一致性(a)还是相对一致性(c);w代表单个评分(s)还是评分均值(a)。

若每个应试者的应聘部门不同，对每个应试者进行素质评分的考官可从不同部门的众多考官中随机抽取，此时基于单因素方差分析模型的ICC比较适宜。由表3可知，单个评分相对一致性ICC估值为0.17，说明评分的变异中只有17%可由相应模型系统解释，83%的变异是随机误差造成的，也就是说评分中存在严重的误差；这说明对于同一应试者的不同单个评分间相关性较差或者说该评分的可信程度很低，进而基于此数据进行的统计分析是不可信的。此时可采用多位考官评分均值进行素质评分，但表3显示4位考官评分均值的相对一致性ICC估值为0.44，说明4位考官评分均值的可靠性虽较单个评分提高不少但仍较低。尽管可通过增加评分考官人数的方法继续提高ICC，但相应支出也是必须要考虑的。无论是置信区间估计还是假设检验结果都没有证据反对ICC=0的原假设。

表2 应试者素质评分

表3 ICC统计分析

若6个应试者的应聘部门都相同且较常见，对应试者进行素质评分的考官可从同一部门的众多考官中随机抽取，此时基于两因素随机效应模型的ICC比较适宜。由表3可知，单个评分间的相对一致性ICC为0.72，说明不同考官评分数值上的一致性或可靠性较好；绝对一致性ICC为0.29，说明不同考官评分之间的相关性较差。引入均值评分后的绝对一致性ICC为0.62，虽有提高，但仍不佳。但无论是置信区间估计还是假设检验结果都显著拒绝ICC=0的原假设。

若6个应试者的应聘部门都相同且比较特殊，对应试者进行素质评分的考官是该企业仅有的面试过该部门应试者的4位考官，此时基于两因素混合效应模型的ICC比较适宜。

六、结 论

组内相关系数应用广泛，但其涉及的理论基础大多数文献只给出结论未给出证明，本文进行了相应的补充。本文还通过软件实现过程及事例分析详细说明了组内相关系数应用中所涉及到的整个模型选择过程。希望本文对组内相关系数的应用者能有一定的帮助。

[1] Cicchetti D V. Guidelines, Criteria, and Rules of Thumb for Evaluating Normed and Standardized Assessment Instruments in Psychology[J]. Psychological Assessment, 1994,6(4).

[2] McGraw K O, Wong S P. Forming Inferences about Someintraclass Correlation Coefficients[J].Psychological Methods, 1996,1(1).

[3] Bartko J J. The Intraclass Correlation Coefficient as A Measure of Reliability[J]. Psychological Reports, 1966, 19(1).

[4] Shrout P E, Fleiss J L. Intraclass Correlations: Uses in Assessing Rater Reliability[J]. Psychological Bulletin,1979,86(2).

[5] Bliese P D. Within-group Agreement, Non-independence and Reliability: Implications for Data Aggregation and Analysis[C]∥ Klein K J, Kozlowski S W J. Multilevel Theory, Research, and Methods in Organizations: Foundations, Extensions, and New Directions, San Francisco: Jossey-Bass,2000.

[6] 余红梅，罗艳虹，萨建，等．组内相关系数及其软件实现[J]．中国卫生统计,2011,28(5)．

[7] Kim H Y. Statistical Notes for Clinical Researchers: Evaluation of Measurement Error 1: Using Intraclass Correlation Coefficients[J]. Restorative Dentistry & Endodontics, 2013,38(2).

(责任编辑：张治国)

Theoretical Basis and Modeling Application of Intraclass Correlation Coefficient

QIAO Jian

(College of Sciences,China University of Mining & Technology (Beijing), Beijing 100083, China)

This paper presents the theoretical basis, the step of modeling application, the implementation of Software, the statistical analysis of actual data for statistical index: intraclass correlation coefficient used in measurement of data reliability; gives the detail description about the selection of model in ANOVA, the distinction between consistency and absolute consistency, the interpretation of the analysis results.

intraclass correlation coefficient; random effects model; mixed effects model

2016-03-31；修复日期：2016-07-15

乔 舰，男，山东肥城人，经济学博士，讲师，研究方向：统计建模。

O212

A

1007-3116(2016)11-0044-05