SIM(2)引力规范理论

吴奕障,薛迅

(华东师范大学物理系，上海200241)

SIM(2)引力规范理论

吴奕障,薛迅

(华东师范大学物理系，上海200241)

基于宇宙微波背景辐射(Cosmic Microwave Background Radiation,CMB)的各向异性观测结果和马赫原理,假设了洛伦兹(Lorentz)对称性从大于星系尺度开始破缺,并基于这个动机以SIM(2)规范理论为例,诠释了所谓的“暗物质效应”,意即天文观测上对牛顿—爱因斯坦(New ton-Einstein)引力理论预言的偏离,可以由小尺度上Lorentz对称性的破缺在大尺度上的累积呈展出来.分析了SIM(2)规范理论,在场运动方程之外得到了8个约束方程,并且将独立contorsion分量个数也约化到了8个.得到了contorsion是非平庸的,并且即使在没有物质分布的区域也会贡献一个等效的能—动张量分布.最后,分析了在弱场近似下的度规柱对称解,分析了此解的性质.

SIM(2)群;洛伦兹破缺;引力规范理论;contorsion

0 引言

广义相对论是当代物理学中最重要的理论之一.随着量子场论,特别是其中规范理论成功地统一了弱电理论,加上大统一理论(Grand Unified Theory,GUT)的铺建,人们逐渐开始思考是否可以将广义相对论,也就是引力理论容纳到规范场论之中去.Utiyama在1955年首先提出了将广义相对论看成是一种规范理论的思想[1],他得出了规范势是克氏符,规范场强是黎曼张量.Kibble在1960年基于Utiyama的基础,将这个理论更加形式化[2].杨振宁在1974年也用他自己的Yang-M ills理论将引力规范化[3].

Lorentz对称性是当代物理学的基础.自从麦克斯韦方程组的问世,爱因斯坦在看到麦克斯韦方程组美妙的同时,也看到了这个方程组是有Lorentz对称性的.这一观点彻底颠覆了牛顿时代的时空观.爱因斯坦将这个对称性用在了他的第一个理论——狭义相对论中.随着时间的推移,物理学家们开始思考如果没有Lorentz对称性会产生怎样的物理,而这些暗示出现在了大尺度的物理图像上.

CMB是宇宙早期光子退耦时的辐射.从CMB的数据可以看到,我们的本星系团相对于CMB静止参考系以627±22 km/s的速度沿银经l=263.99◦±0.14◦,b=48.26◦±0.03◦方向运动,这个运动导致偶极矩各向异性.从理论角度看,CMB静止参考系的存在即使在远离任何星系的地方都破坏了Lorentz协变性[4].CMB数据还存在低多级矩和其他反常,诸如非常大尺度的各向异性、反常排列和非高斯分布等,其中持续时间最长的争论来自于低-l多级矩：球玉展开l=2的四级矩振幅与大爆炸预言相比过低,l=3的四级矩与八级矩模式间有无法解释的联系并与黄道面和黄道面与天球赤道两个交点连线有联系,这个连线也被称为邪恶轴心[5].

马赫原理说明局域惯性标架由大尺度物质分布确定,其可以被更一般地陈述为：局域物理规律由宇宙的大尺度结构确定[6].这为我们思考大尺度上Lorentz对称性的问题提供了参考.

CMB的非各向同性以及对马赫原理的思考暗示了Lorentz对称性在小尺度上破缺而在大尺度上累积成客观效应的可能性.

1999年,Coleman和Galshow提出了偏离Lorentz对称性的一个模型[7].这个模型保时空平移以及空间转动不变性,而允许对伪转动的改变;这个模型用一个常的类时4矢(刺矢)来参数化.而后Colladay和Kostelecky引入了更一般的刺矢导致的扰动,这些量可以看成是由于Lorentz对称性破缺而导致的某些张量的非零的真空期望值[8].

2000年,Amelino-Camelia提出了双狭义相对论[9].这个理论也称为有两个观测者不依赖尺度的狭义相对论：一个是有速度量纲的c;一个是有质量量纲的κ.前者可以认同为光速,后者可以认同的Plank质量;而在κ→∞时理论回到狭义相对论.因此这个理论本身是狭义相对论破缺的.

CPT(Charge conjugation-Parity-Tim e reversal,CPT)对称性也是当代物理的最严格的对称性之一;而这个对称性和Lorentz群有着非常紧密的联系.我们发现,在某些理论中CP和P会出现破缺,这暗示着P、T对称性并非是严格不变的.而Lorentz群(固有)加上P、T对称性才是最大Lorentz群.这就暗示,Lorentz群(固有)也可能会破缺.

2006年,Cohen和Glashow提出了狭义相对论对称性破缺的机制,这个理论称为非常狭义相对论[10].时空对称性不再是Lorentz群(Poincare群),而是Lorentz群的子群：E(2)；HOM(2)；SIM(2).他们发现狭义相对论中要求的时间变化、速度叠加等不需要Lorentz群而只需要其子群就可以实现.其条件是,子群加入P、T就可以扩张成完整的Lorentz群.在这些子群中,破缺程度最小的就是4生成元子群SIM(2)群.2007年, Gibbons、Gomis和Pope提出了SIM(2)群作为时空局部对称群模型,他们发现这个模型具有Finsler几何的性质[11].

我们以SIM(2)群为局域规范对称群,并将其用于规范理论.

1 SIM(2)引力规范理论

本文的一些记号规范参考了文献[12-13].

Lorentz度规的表达式为

定义标架haµ,它满足

其结构系数可以表示为

因此

Lorentz李代数有6个独立生成元,其满足的对易子为

其中,对应角动量生成元的为

对应伪转动(boost)生成元的为

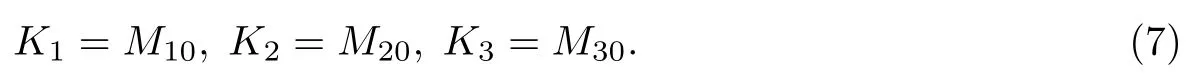
用角动量和伪转动生成元表示,对易关系可以写成

SIM(2)生成元为

Lorentz联络Aµ具体展开的形式为

Mab对下标反称,这使得与其缩并的Aabµ也是反称的.这个联络定义的协变导数算符为

实际上,Mab是Lorentz李代数的表示,由于我们选择切空间,故为Lorentz群的矢量表示.

为了将李代数限制在SIM(2)上,我们施加限制方程

有了这样的限制,就从Lorentz时空规范理论得到SIM(2)时空规范理论.

与Aabµ相对应的线性联络Γρνµ满足

这可以分解为克氏符和contorsion

Acab写成fcab以及挠率Tcab的函数,满足

曲率和自旋联络间满足

可以写成时空指标的形式

仍然将拉氏量选取为标量曲率.根据曲率张量,标量曲率可以写为

Lorentz时空规范理论的作用量是Hilbert作用量,而SIM(2)时空规范理论有两个约束,相当于要再作用两个约束乘子项,作用量为

我们对自旋联络做变分,结果为

其中,

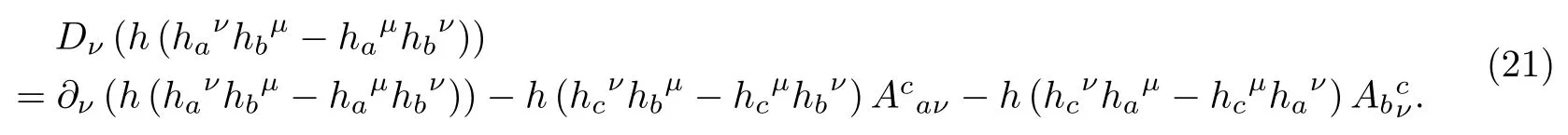
这个结果可以写为

由于

因此对SIM(2)规范理论,即使是没有物质场的情况下,挠率也不再为0.我们得到

对其他的(a,b)有

对标架变分

由于约束方程,我们得到的动力学方程在形式上和Einstein方程一样

我们仍然将此称为Einstein方程.但要注意两点：第一,实质上这个方程还要和约束方程联立,因此,曲率和Hilbert作用量的结果不同；第二,这个方程的contorsion并不为0,因此其规范势和广义相对论的不同.

我们具体的求解思路是将所有的量都表达为contorsion K和结构系数f的表达式.

将自旋联络写成contorsion的形式有

其中,

约束条件可以用contorsion和f表达

我们用contorsion表达

可以写成

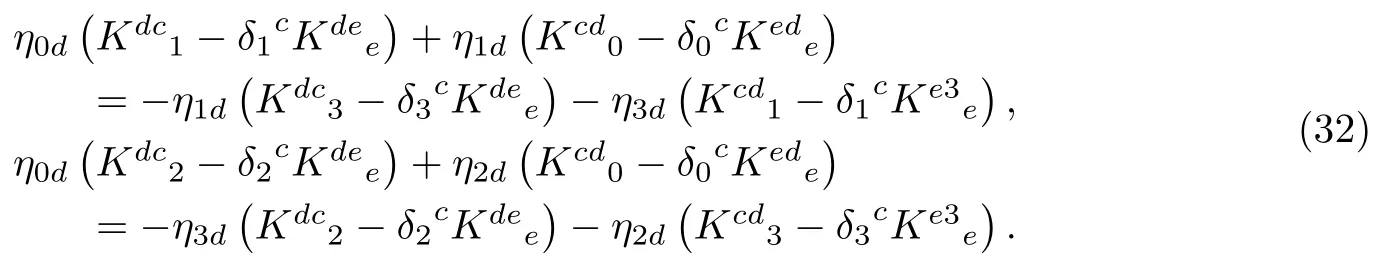
对得到的

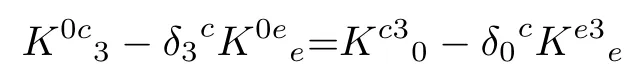
和

联立,就能得到

以及

以及

我们发现独立的contorsion变成了8个,而限制方程也为8个,因此正好能够求解.

另一方面,对标架求变分得到的Einstein方程在时空指标下可以写为

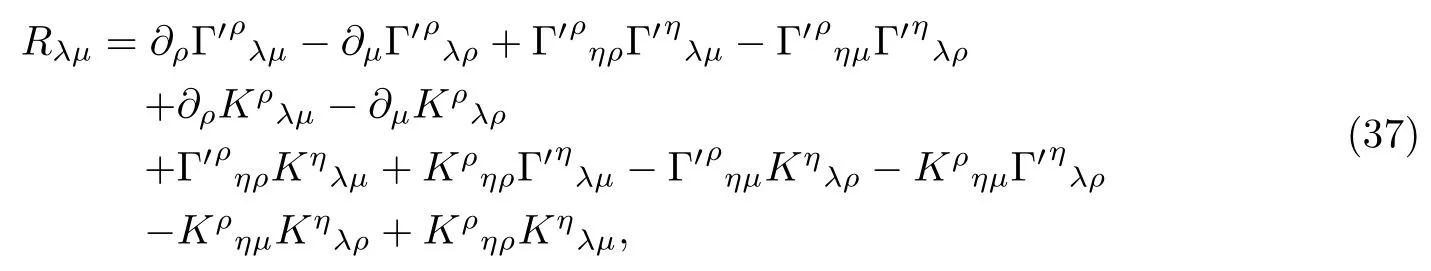
其中,Kµνρ=haµhbνhcρKabc.式(37)的第一行就是里奇张量,余下部分就是时空指标的contorsion的贡献.这又给出10个方程,加上10个度规分量,因此,总共是18个未知量和18个方程.

我们求解的是真空Einstein方程.我们将里奇张量记作˜Rλµ,则真空方程可以写成

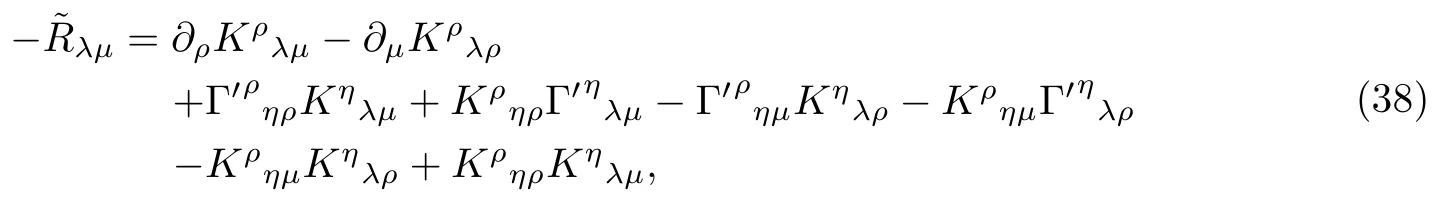
这相当于求解一个非真空的方程.实际上,对Einstein方程

我们选取一般柱对称系,度规张量为一般柱对称度规

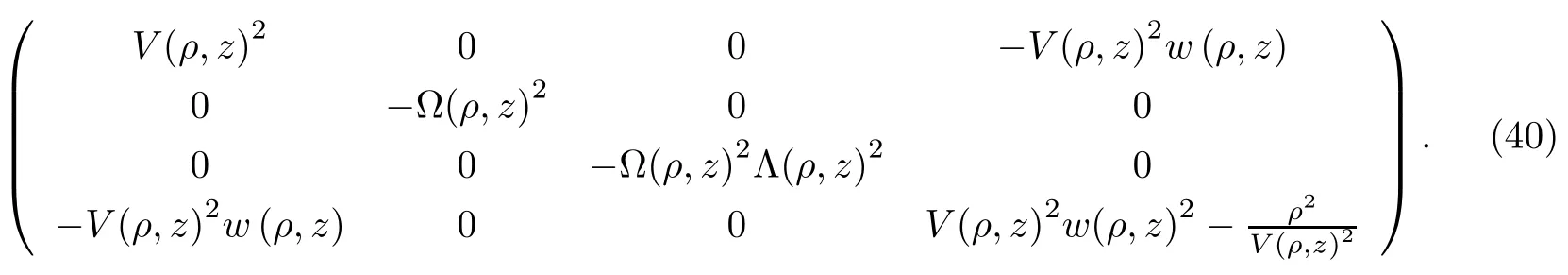
选取合适的Lorentz变换,要求满足8个约束方程.史瓦西度规在恒星或星系尺度下是D氏度规的弱场近似,其特征参数为,其中,Rc是恒星或星系尺度,c是光速,G是万有引力常数,M是恒心或星系的质量(如太阳的这个参数就约等于2×10-6).我们也要求柱对称度规满足弱场近似(但不要求远场是弱场),并用这个特征参数(为简单起见,记作ε)作为展开参数.展开到一阶,我们发现满足约束的度规的形式为

将这个结果代入场方程,发现在一阶情况下V(ρ,z)=0.接下来,我们分析这个度规的性质.对四速有

由于运动轨迹在一个平面上,我们选择一个平面.根据度规我们看到2个Killing矢量：由此可以定义两个守恒量

和

其中,E是能量,L代表角动量.将度规和守恒量代入可得

可以看出有效势为

我们发现这个度规没有引力势,只有离心势.这导致没有稳定的轨道,一旦受到径向的微扰就会趋向无穷远处.

[1]UTIYAMA R.Invariant theoretical in terpretation of interaction[J].Physical Review,1956,101：1597-1607.

[2]KIBBLE TW B.Lorentz invariance and the gravitational field[J].Journal of Mathematical Physics,1961(2)：212-221.

[3]YANG C N.Integral formalism for gauge fields[J].Physical Review Letters,1974,33：445-447.

[4]ARKANI-HAM ED N,CHENG H,LUTY M,et al.Universal dynamics of spontaneous Lorentz violation and a new spin-dependent inverse-square law force[J/OL].Journal of High Energy Physics,2005：JHEP 07[2005-07-13]. http：//dx.doi.org/10.1088/1126-6708/2005/07/029.

[5]SCHWARZ,D.J,STARKM AN G D,HUTERER D,et al.Is the low-l microwave background cosmic？[J]. Physical Review Letters.2004,93：221301.

[6]HAWKING S W,ELLIS G.Large scale structure of space-time[M].Cambridge：Cambridge University Press, 1973.

[7]COLEMAN S R,GLASHOW S L.High-energy tests of lorentz invariance[J].Physical Review D,1999,59：116008.

[8]CILLADAY D,KOSTELECKY V A.Lorentz-violating extension of the standard model[J].Physical Review D, 1998,58：116002.

[9]AMELINO-CAMELIA G.Testable scenario for relativity with minimum length[J].Physics Letters B,2001,510：255-263.

[10]COHEN A G,GLASHOW S L.Very special relativity[J].Physical Review Letters,2006,97：021601.

[11]GIBBONS G W,GOMIS J,POPE C N.General very special relativity is finsler geometry[J].Physical Review D,2007,76：081701.

[12]RAMOND P.Field Theory：A Modern Primer[M].Colorado：Westview Press,1997.

[13]ALDROVANDI R,PEREIRA J G.Teleparallel Gravity[M].New York：Sp ringer,2013.

(责任编辑：李艺)

SIM(2)gravitational gauge theory

WU Yi-wei,XUE Xun
(Department of Physics,East China Normal University,Shanghai 200241,China)

Based on the anisotropies of CMB(Cosmic Microwave Background Radiation, CMB)on the large scale and Mach’s principle,this paper proposed that the Lorentz invariance is violated from the length scale of galaxy.SIM(2)gauge theory was taken as an example of such motivation to illustrate the so called dark matter effect,the deviation of astronomical observation from New ton-Einstein prediction,which can be emerged from the accumulated Lorentz violation effect on the short scale.SIM(2)gauge theory was analyzed and 8 additional constrain equations were obtained in addition to the equation of motion,while the independent components of contorsion were also reduced to 8.It can lead us to the conclusion that the contorsion is non-trivial and can contribute an effective energy-momentum distribution even in the region devoid of matter.Finally,the cylindrical symmetrized solution of metric under weak field expansion was given and its property was analyzed.

SIM(2)group;Lorentz breaking;gravitational gauge theory;contorsion

O41

A

10.3969/j.issn.1000-5641.2016.03.009

1000-5641(2016)03-0076-08

2015-05

吴奕<,男，硕士研究生,研究方向为洛伦兹破缺、等效引力理论、与暗物质有关的超越标准模型理论.E-mail：longqi07@qq.com.

薛迅,男,副教授,硕士生导师,研究方向为洛伦兹破缺、等效引力理论、与暗物质有关的超越标准模型理论.E-mail：xxue@phy.ecnu.edu.cn.