一维对流扩散方程柯西问题解的Lp衰减估计

曾妍,辛谷雨

(1.河海大学理学院,南京211100;2.中国电子科技集团公司第二十八研究所,南京210007)

一维对流扩散方程柯西问题解的Lp衰减估计

曾妍1,辛谷雨2

(1.河海大学理学院,南京211100;2.中国电子科技集团公司第二十八研究所,南京210007)

考虑一维空间对流扩散方程解的Lp(2≤p≤∞)衰减估计,利用格林函数、频谱分析、能量估计等方法得到了解有与热核算子相同的衰减速度.

对流扩散方程;Lp衰减;频谱分析;格林函数;能量估计

0 引言

本文考虑对流扩散方程

的满足初值条件c(x,0)=c0(x)的解的Lp(2≤p≤∞)衰减估计,其中c代表溶质中的溶液浓度,t代表时间变量,x代表空间变量并且x∈R,u是常数,代表流速,D是扩散系数,非线性项f(c)=c2.

许多数学家对对流扩散方程进行了大量研究,取得了很多成果.Mahmoud Qafsaoui在[1]中研究了非线性对流扩散方程

在Rn×(0,∞)上的解的高阶导Dru(t)在Lp范数意义下的大时间渐近性质,其中a代表常向量,Γ是高阶椭圆算子,Ψ是非线性项并且Ψ(0)=0,Θ≥1.他们得到,若m≥2并且

则对于∀p∈[1,∞),t＞0,有

本文中,我们用C代表一般常数,Wm,p(R)(m∈N+,p∈[1,∞))是Sobolev空间,并且有,特别地Hs：=Ws,2.傅立叶变换定义为,所有的卷积都是关于空间变量x的.本文是在[3]中解的L2衰减估计的基础上得到的Lp衰减估计,所以我们先列出[3]的结论.

定理0.1当D＞u,l≥1,E=m ax(‖c0‖Hl,‖c0‖L1)充分小时,c(x,t)满足

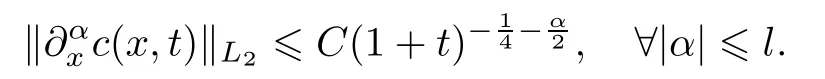
在定理0.1的基础上,我们得到本文结论：

定理0.2当D＞u+1,l≥1,E=max(‖c0‖Hl,‖c0‖L1)充分小时,c(x,t)满足

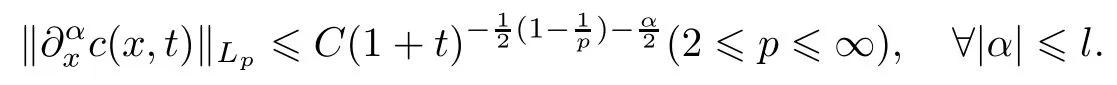
本文安排如下：在第一节中,我们给出(0.1)的解的表达式以及一些基本估计;解的L∞衰减估计将在第二节中给出;最终Lp估计可由L2、L∞估计以及插值不等式得到.

1 解的表达式

由常微分方程求解得

则(0.1)的解可表示为

作光滑截断函数

基于傅立叶变换和(1.5),我们定义函数m(x)的低、高频分解如下

这里χ(D)是χ(ξ)确定的拟微分算子.

引理1.1当D＞u时,存在常数C,使得

证明由Hausdorff-Young不等式,有

引理1.2设cH(x,t)=(1-χ(D))c(x,t),这里cH(x,t)是方程(1.6)的解,χ(D)是(1.5)式定义的分解算子,则cH(x,t)满足

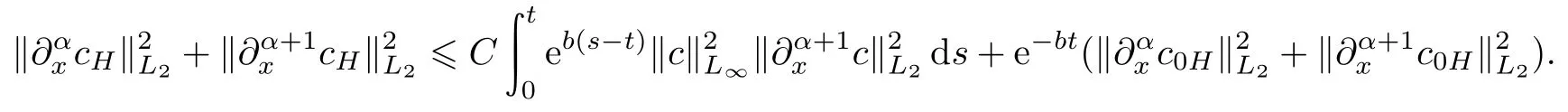
证明由方程(1.6),我们有

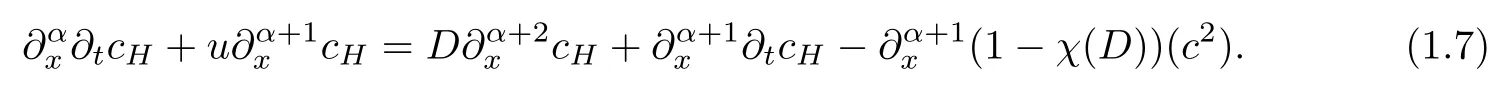
由文献[4]注2.1知

由(1.8)—(1.10),又因为

所以

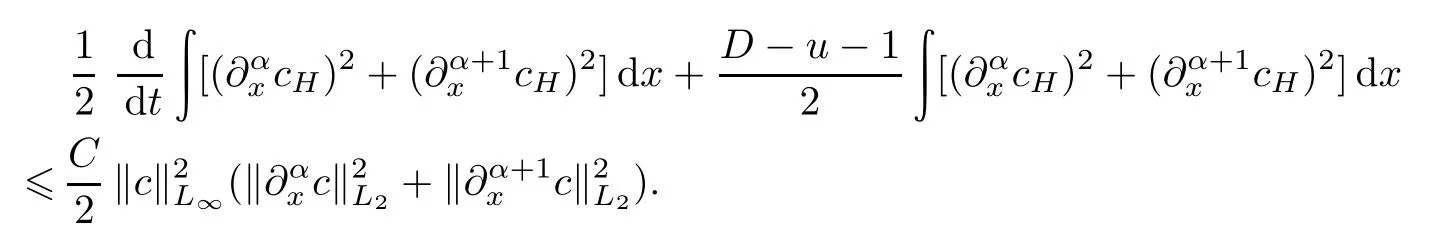
令b=D-u-1,当D-u-1＞0时,有

由(1.11)得

2 解的L p衰减估计

由引理1.1知

由定理0.1和引理1.1知

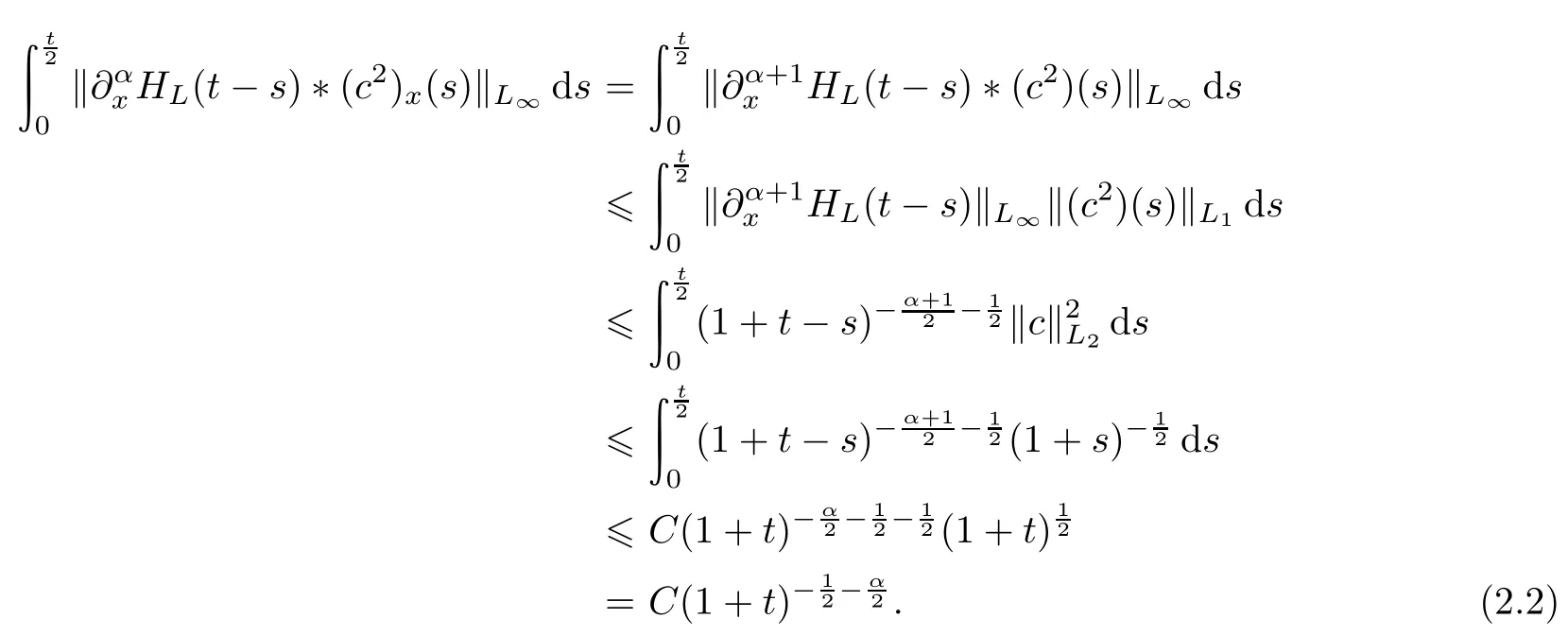
由定理0.1知

由引理1.1和(2.3)式知

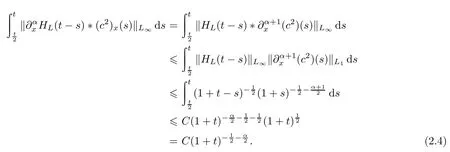
由引理1.2知

由Sobolev嵌入不等式及(1.12)式知,

由定理0.1知

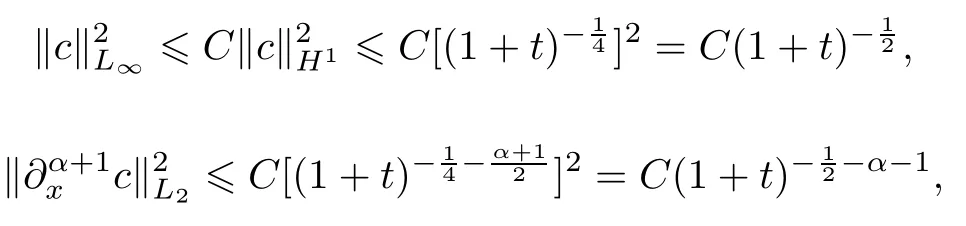
所以

由(2.1)—(2.7)知

由文献[5]知,插值不等式为

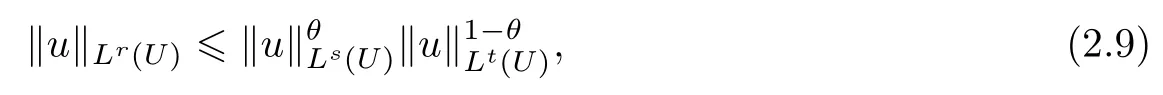
[1]QAFSAOUI M.Large time behavior for nonlinear higher order convection-diffusion equations[J].Ann I H Poincaré-AN,2006,23：911-927.

[2]ESCOBEDO M,ZUAZUA E.Large time behavior for convection-diffusion equations in Rn[J].J Func Anal, 1991,100(1)：119-161.

[3]徐红梅,曾妍.一维对流扩散方程解的L2衰减估计[J].武汉大学学报(理学版),2015,61(6)：573-576.

[4]DENG S J,WANG W K,ZHAO H L.Existence theory and Lpestimates for the solution of nonlinear viscous wave equation[J].Non linear Analysis：Real World Applications,2010,11(5)：4404-4414.

[5]EVANS L C.Partial Differential Equations[M].New York：American Mathematical Society,2010.

(责任编辑：林磊)

Lpestimates of solutions to the Cauchy problem of one-dimensional convection-diffusion equations

ZENG Yan1,XIN Gu-yu2
(1.College of Science,Hohai University,Nanjing 211100,China; 2.The 28th Research Institute of China Electronics Technology Group Corporation, Nanjing 210007,China)

This paper investigated the Lpestimates of solutions to one-dimensional convection-diffusion equations,using Green’s function method,frequency decomposition and energy estimates.We found that the decay rate of the solution is the same as that for heat fusion operator.

convection-diffusion equation;Lpestimates;frequency decomposition; Green’s function;energy estimates

O 157.28

A

10.3969/j.issn.1000-5641.2016.03.003

1000-5641(2016)03-0021-06

2015-05

国家自然科学基金(11101121)

曾妍,女,硕士研究生,研究方向为偏微分方程.E-mail：1651054563@qq.com.