一类带有界面条件的奇异摄动弱非线性边值问题

吴成龙

(东华大学应用数学系,上海201620)

一类带有界面条件的奇异摄动弱非线性边值问题

吴成龙

(东华大学应用数学系,上海201620)

研究了带有界面条件的弱非线性边值问题,信助Schauder不动点定理建立带有界面条件的弱非线性边值问题的上下解理论,通过边界层函数法构造形式渐近解,证明解的存在性.

奇异摄动;渐近展开;微分不等式

0 引言

考虑弱非线性边值问题

其中ε是一个小的正参数,A和B是给定的常数,而且

其中[y](d)=y(d+)-y(d-),因右端函数在x=d处的不连续性,该问题的解及解的一阶导数在x=d∈(a,b)有一个跳跃,因此可以将该问题看成由左问题和右问题组成的.

奇异摄动理论产生于对天体力学的研究,由于其在非线性问题中的广泛应用,相关理论和方法不断被发展和优化[1-5]等.最近几年,带有界面条件的奇异摄动理论结果被广泛地应用于复合材料的热传导中[6],以及人口基因模型中[7],因此带有界面条件的边值问题的研究越来越受到关注,如谢峰在文献[8]中研究了带有界面条件的二阶拟线性奇异摄动Dirichlet问题

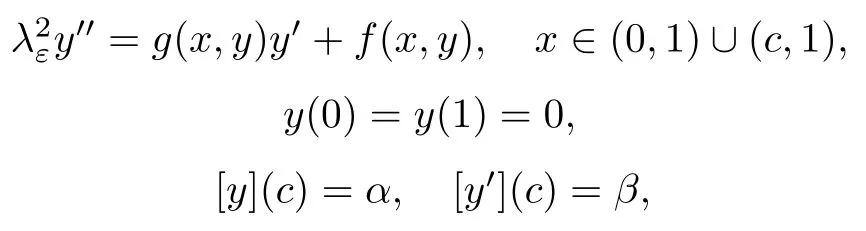
其中

作者建立了界面条件的拟线性边值问题的上下解理论,并给出了带有界面条件的二阶拟线性边值问题的解存在和唯一的条件.

对于弱非线性奇异摄动边值问题,也有很多人对其研究,如丁海云,倪明康在文[9]中对下列具有不连续源的弱非线性奇异摄动边值问题进行了研究.

作者证明了解的存在唯一性与渐近解的一致有效性.本文对弱非线性奇异摄动边值问题与带有界面条件的二阶拟线性奇异摄动Dirichlet问题进行推广,研究带有界面条件的弱非线性奇异摄动边值问题.

本文第一部分主要通过Schauder不动点定理建立带有界面条件的弱线性边值问题的上下解理论.第二部分主要通过边界层函数法,求出问题的渐近解,再由渐近解寻找上下解.第三部分通过实例分析验证结果.

1 基本定理

为了方便研究,我们使用文[10]中的记号,空间Qj[a,b],j=1,2,定义为

这里的Ω={d,x1,x2,···,xk}.

定义Q1[a,b]空间下的范数为：

可以证明Q1[a,b]是一个Banach空间.

接下来我们考虑如下带有界面条件的边值问题

显然(4)—(6)的解属于Q2[a,b].

定义1如果α(x)∈Q2[a,b]满足以下条件：

我们就称α(x)是(4)—(6)的一个下解.

如果β(x)∈Q2[a,b]满足以下条件：

我们就称β(x)是(4)—(6)的一个上解.

(H 0)f(x,y,y′)关于函数对α(x)和β(x)满足Nagum o条件,即存在ϕ(x)∈C1[0,+∞), ϕ(x)＞0,使得

如果f(x,y,y′)：,且f(x,y,y′)关于函数对α(x)和β(x)满足Nagumo条件.则由文[11]知,存在N＞0,使得

定理1假设问题(4)—(6)存在上下解ϕ(x),φ(x)(ϕ(x)≤φ(x)),且f(x,y,y′)关于函数对ϕ(x)和φ(x)满足Nagumo条件,则问题(4)—(6)至少存在一个解y(x)∈C2([a,d)∪(d,b]),且解y(x)满足

证明首先修正原问题F(x,y,y′)=f(x,y,y′)-y,

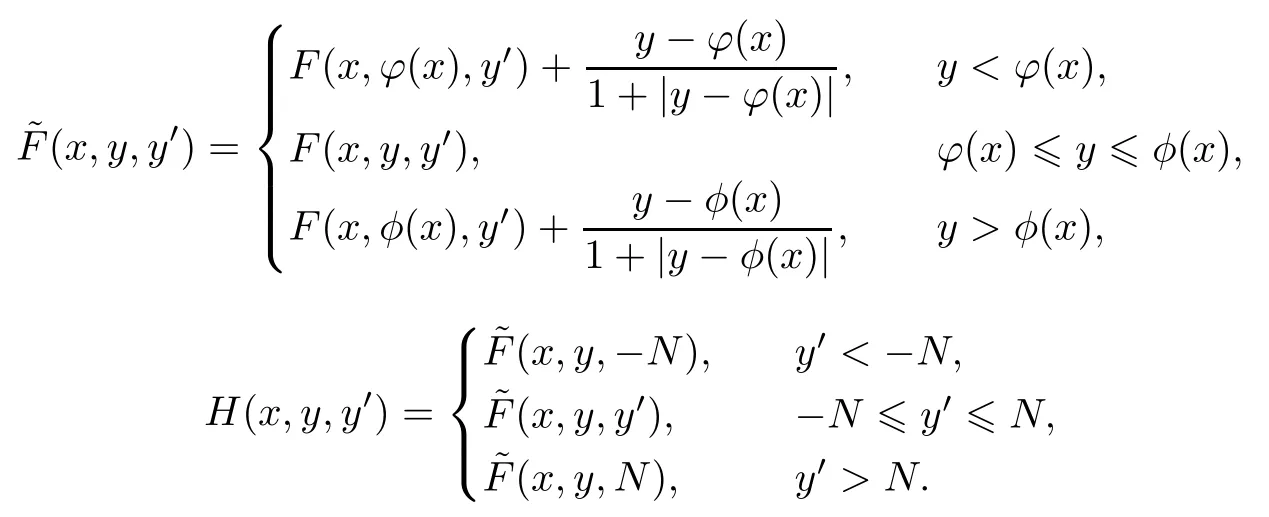
这样修正后的问题变为

利用Green函数写出等价的积分方程,

其中p(x)是下面方程的解

显然,p(x)∈[a,d)∪(d,b]在x=d处不连续,

所以

这里的K1=ed-b,K2=ea-d.

Green函数G(x,s)满足如下边值问题

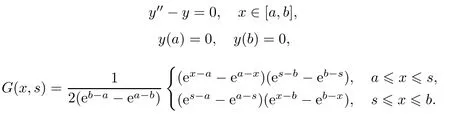
定义如下算子T：Q1[a,b]→Q1[a,b],

Q1[a,b]是一个Banach空间,由文[8]引理2.1可知,如果有界函数族E⊂Q1[a,b]在[a,b]上分段等度连续,则E是一个相对紧集.从而知算子T是一个全连续算子.由Schauder不动点定理知,算子T至少存在一个不动点y(x)∈Q1[a,b].

接下来证明解y(x)满足ϕ(x)≤y(x)≤φ(x),我们这里只证明ϕ(x)≤y(x).

若不然,令h(x)=y(x)-ϕ(x),则至少存在一点x′使得h(x′)＜0,不妨设x0是一个最小的负值点,先假设,显然我们知,h(x0)＜0,h′(x0)=0,h′′(x0)≥0.但是

若x0=d,则有

即h(x)在d点连续.又注意到h(x)在d点取得负的极小值,故h′(d+)-h′(d-)≤0.但是

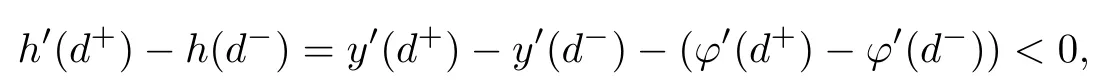
这导出矛盾.如果x0=xi,同样可以推出矛盾,我们证明了ϕ(x)≤y(x),x∈[a,d)∪(d,b].同样的方法我们也可以证明y(x)≤φ(x),x∈[a,d)∪(d,b].

因此,问题(12)—(14)的解也是问题(4)—(6)的解,同时也满足ϕ(x)≤y(x)≤φ(x),x∈[a,d)∪(d,b],定理1证明结束.

2 主要结果

这部分主要讨论形式渐近解.为简单计,这里只考虑零阶近似.因为在x=d处,函数不连续,所以把原始问题(1)—(3)看成左问题和右问题构成.

左问题PL：

右问题PR：

首先做如下假设：

(H 1)原问题的退化问题f1(x,y,0)=0,x∈[a,d],有解ϕ(x)∈C1[a,d];f2(x,y,0)= 0,x∈[d,b],有解φ(x)∈C1[d,b].

(H 2)函数f1(x,y,εy′)∈C2(R×R×[a,d]),f2(x,y,εy′)∈C2(R×R×[d,b]),

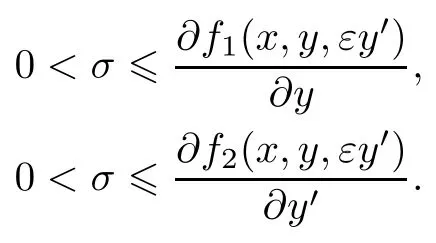
由边界函数法[4],设问题(15)—(16)的形式解为

其中

将(19)式代入(15)式可得到一系列确定展开式系数的方程

满足左边界层x=a条件

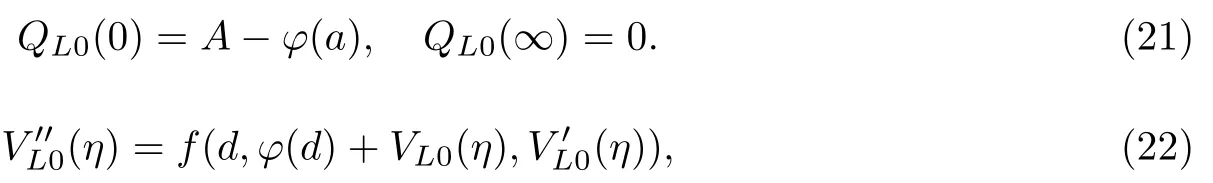
满足右边界层x=d条件

同样的方法,可以求出右问题PR的形式渐近解

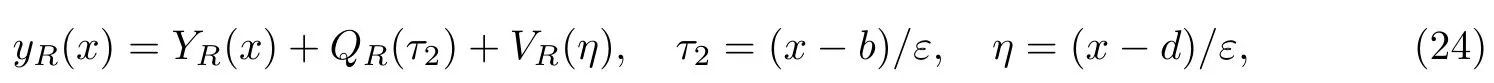
其中

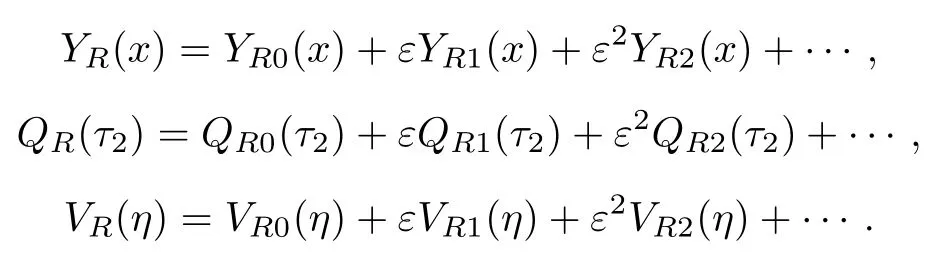
将(24)式代入(17)式可得到一系列确定展开式系数的方程.

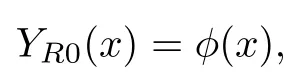
则右问题PR的左边界层与右边界层满足的条件如下：

为了求出零阶渐近解,接下来引入两个引理,是关于渐近解的指数估计[5].

引理1若条件(H1)—(H2)成立,只要ε＞0充分小,则问题(20)和(21)存在一个解QL0(τ1),且解满足如下指数估计：

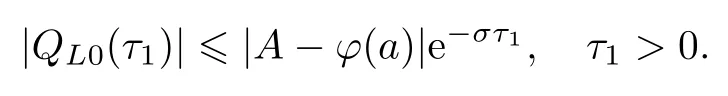
引理2若条件(H1)-(H2)成立,只要ε＞0充分小,则问题(22)和(23)存在一个解VL0(η),且解满足如下指数估计：

同样的方法,我们可以对右问题PR做出如下指数估计：

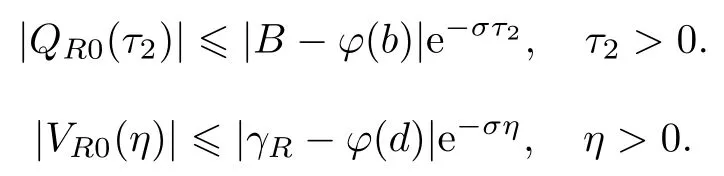
由上面引理,QR0(τ2)在点d处指数型衰减,可以忽略,所以当我们考虑右边界层问题时,无需考虑左边界层的影响.

由界面条件知：

即

式中

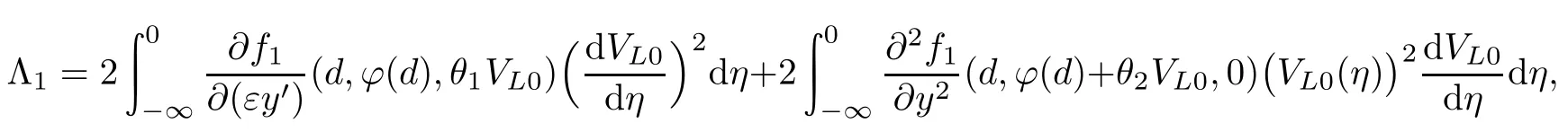
这里θ1,θ2∈(0,1).

同样的方法,我们可以得出右问题PR的左边界层的一阶导数表示

式中

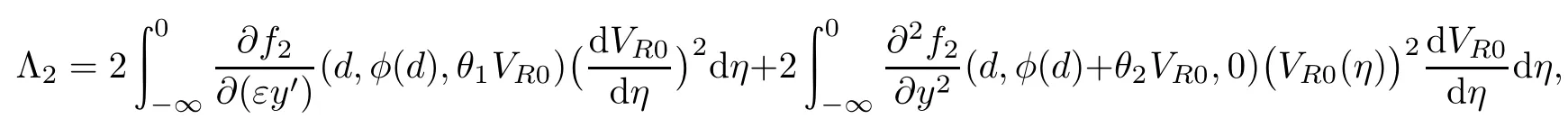
这里θ3,θ4∈(0,1).则

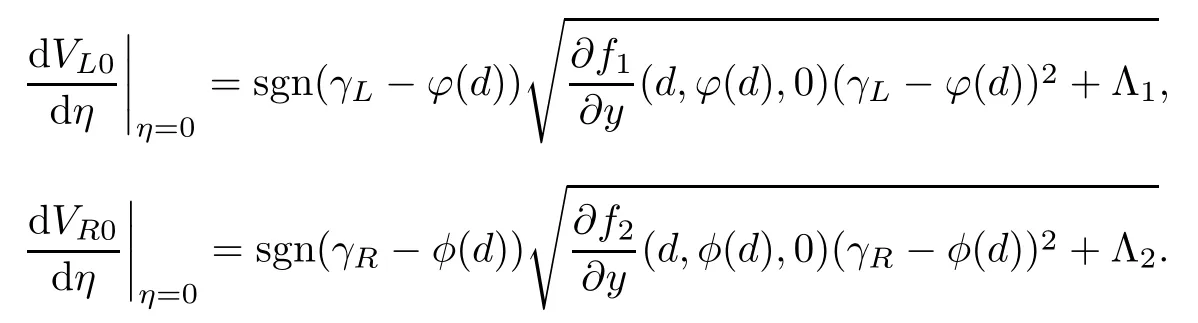
从而,

(H 3)假设方程组(31)—(32)有解(γL,γR).

至此,我们已构造出原问题(1)—(3)的零阶形式近似解

定理2如果条件(H0)—(H3)成立,对足够小的ε＞0,边值问题(1)—(3)至少存在一解y(x,ε)∈Q1[a,b],且

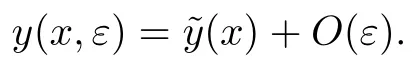
证明为了证明定理2,接下来寻找问题(1)—(2)的上下解.首先,对于上面的零阶渐近解,如果条件(H1)—(H3)成立,则显然有如下不等式成立.

接下来通过零阶近似构造上下解：不妨设上下解分别为α(x),β(x),其中

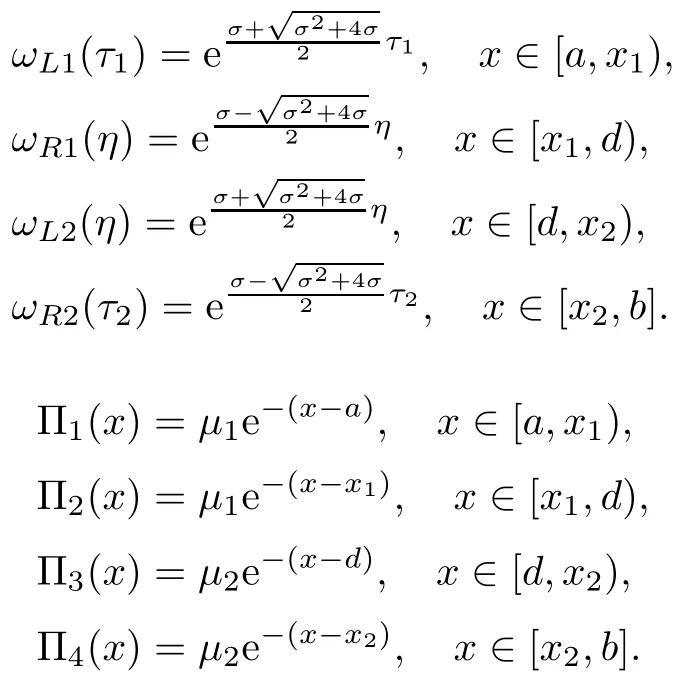
这里的µi,i=1,2,满足如下条件：

可以选取合适的µ1,使得µ1＞0.同样的方法,可以求出µ2.

这里的λi,i=1,2,3,4满足如下条件：

对于以上的构造的Π1(x),i=1,2,3,4,以及ωL1(τ1),ωR1(η),ωL2(η),ωR2(τ2)具有以下性质

(i)ωL1(τ1),ωR1(η),ωL2(η),ωR2(τ2)是非负的;

(ii)

(iii)ωL1(τ1),ωL2(η),ωR1(τ1),ωR2(η)是以下方程的解

(iv)这里的Πi(x),i=1,2,3,4,是下面方程的解

则对于以上构造的上下解,显然满足如下性质：

接下来验证(7),不妨设x∈[a,x1),

同理可以验证β(x)也是问题(4)—(6)的一个上解,即边值问题(4)—(6)存在一解y(x,ε)∈Q1[a,b]且满足

证毕.

3 例子

考虑如下奇异摄动问题：

显然可知,左问题的退化问题f1(x,y,εy′)=2y-2=0有唯一光滑解：

而右问题的退化问题f2(x,y,εy′)=y=0也有唯一光滑解：

则(20)—(21),(22)—(23),(25)—(26),(27)—(28)的解可以求出：

[1]莫嘉琪.关于非线性方程εy′′=f(x,y,y′,ε)奇异摄动边值问题解的估计[J].数学年刊,1984,5A(1)：73-77.

[2]MO J Q.Generalized solution of singularly perturbed problems for nonlinear reaction diffusion equation[J]. Journal of Anhui Normal University(Natural Science),2014,2：103-107.

[3]杜增吉,莫嘉琪：一类扰动发展方程近似解[J].物理学报,2012,61(15)：155202.

[4]周明儒,杜增吉,王广瓦.奇异摄动中的微分不等式理论[M].北京：科学出版社,2012.

[5]倪明康,林武忠.奇异摄动问题中的渐近理论[M].北京：高等教育出版社,2009.

[6]MIKHAILOV M,ÖZISIK M.Unified Analysis and Solution of Heat and Mass Diffusion[M].New York：Dover, 1994.

[7]DE FALCO C,O,RIORDAN E.Interior layers in a reaction-diffusion equation with a discontinuous diffusion coefficient[J].Int J Numer Anal Model,2010,7：444-461.

[8]XIE F.An interface problem with singular perturbation on a subinterval[J].Boundary Value Problems,2014, 2014：201.

[9]丁云海,倪明康.具有不连续源的弱非线性奇异摄动边值问题[J].山东大学学报,2012,47(2)：8-13.

[10]LIN H X,XIE F.Singularly perturbed second order semilinear boundary value problems with interface conditions [J].Boundary Value Problems,2015,2015：47.

[11]KELLY W G,PETERSON A C.The Theory of Differential Equations[M].New York：Sp ringer-Verlag,2010.

(责任编辑：林磊)

A class of singularly perturbed weakly non linear boundary value problems with interface conditions

WU Cheng-long
(Department of Applied Mathematics,Donghua University,Shanghai 201620,China)

In this paper we study a class of weakly non linear boundary value problems with interface conditions.By means of the Schauder fixed point theorem we establish the theorem about a weakly nonlinear boundary value problem with interface conditions.By the method of boundary layer function,the formal asymptotic solution is constructed, which is used to prove the existence of the solution.

singular perturbation;asymptotic expansion;differential inequalities

O175.1

A

10.3969/j.issn.1000-5641.2016.03.004

1000-5641(2016)03-0027-12

2015-05

上海市自然科学基金(15ZR1400800)

吴成龙,男，硕士研究生,研究方向为奇异摄动理论.E-mail：2131377@mail.dhu.edu.cn.