基于用户相似度的协同过滤算法改进

王 威， 郑 骏

（华东师范大学计算中心，上海 200062）

基于用户相似度的协同过滤算法改进

王 威， 郑 骏

（华东师范大学计算中心，上海 200062）

协同过滤技术作为目前最常见的个性化推荐技术之一，被广泛认可和应用.作为基于内容的算法执行方式，协同过滤在准确性上具有相当的优势.该算法的核心问题是相似度的计算.本论文介绍了传统协同过滤算法，并对原有的相似度公式进行了优化，使得相似度计算更具有准确性.实验表明，文中提出的优化方法在推荐精度上有显著提高，降低了平均绝对误差（Mean Absolute Error，MAE）.

推荐技术；相似度；协同过滤；MAE

0 引 言

随着人们生活越来越信息化，当面对互联网上浩瀚的信息海洋，人们会显得有些手足无措.如今，很多比较著名的商业组织，如Netflix、Group Lens、Amazon等，都不同程度地使用了各种各样的推荐系统［1-2］，以帮助人们更好地处理日益庞大的互联网信息.推荐系统通过分析用户的行为习惯，将一些有效信息推荐给用户，方便用户能够更快地获取需要的信息，在节省了筛选信息时间的同时，也提高了信息的有效使用率.

在现今的推荐算法中，协同过滤（Collaborative Filtering，CF）［3］被广泛认可和采用，它以其出色的速度和稳健性，在信息过滤和信息系统中炙手可热.协同过滤算法是通过对User-Item评分矩阵的分析，向用户推荐用户感兴趣的商品.实现协同过滤的推荐算法，需要进行3个步骤：第一步收集数据；第二步找到相似用户和物品；第三步进行推荐.就目前而言，协同过滤算法的主流方法有两种：基于用户的协同过滤算法（User-Based CF）［4］和基于物品的协同过滤算法（Item-Based CF）［5-6］.本文中研究讨论的方法是User-Based CF，它的基本思想是根据当前用户对物品的爱好，找到具有相似爱好的其他用户，然后将这些用户喜欢的物品推荐给当前用户.传统协同过滤算法虽然被广泛使用，但是还是存在问题：邻居用户是基于用户间的相似度得出的，但是传统的相似度计算由于考虑的因素不够全面，导致了精度不高.

本文针对这个问题，提出了新的数据加权度量：基于用户相似度的数据权重.将这种权重引入到传统User-Based CF的相似度计算中，可以提高用户相似度计算的精确度.

1 传统User-Based CF

传统User-Based CF是一种以用户为主体的算法，它比较强调的是社会性的属性，也就是说这类算法更加强调把和你有相似爱好的其他用户的物品推荐给你.与之对应的是Item-Based CF，这种方法更加强调把和你喜欢物品相似的物品推荐给你.User-Based CF是根据用户对物品的喜爱程度，在众多用户中找到小部分和当前用户有相似爱好的其他用户，将这些用户组成邻居集合，然后将这些邻居喜欢的其他物品推荐给当前用户.

User-Based CF一般分为3个步骤：表示；邻居用户形成；推荐生成.

1.1 表示

在传统User-Based CF中，输入数据通常是采用用户-项目评分矩阵R（m，n）［7］.R（m，n）是一个m×n阶矩阵，其中m表示所有参与评价的用户的个数，n表示所有被评价项目的个数.对于任意的i＜m和j＜n，Rij表示用户i对项目j的评分.矩阵中的评价值可以是由二进制的0和1来表示，其中0表示用户不喜欢该项目，1表示用户喜欢该项目；也可以用5分制、10分制或其他度量方式来表示，评分越高代表用户喜欢程度越高.本论文中采用的数据集是MovieLens［8］数据集，评分方式采用的是5分制.表1是用户对资源的评分矩阵.

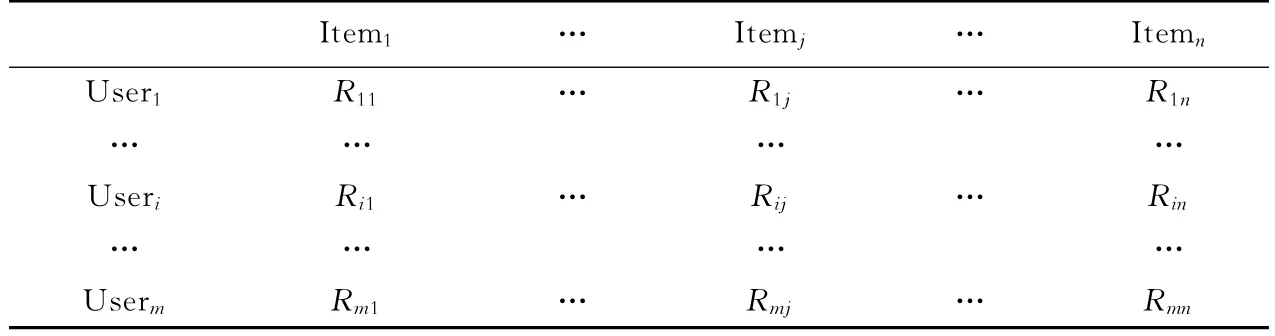
表1 用户-项目评分矩阵Tab.1 User-item rating matrix

1.2 邻居用户形成

在User-Based CF中，邻居用户形成是最关键的步骤.我们可以根据用户-项目评分矩阵R（m，n）计算用户之间的相似度，然后产生一个按照相似度大小排列的邻居集合，这个过程的核心是相似度的计算［9-10］.一般来讲，相似度的计算主要有余弦相似性（Cosine Similar-ity）［11］和皮尔逊相关系数（Pearson Correlation Coefficient）［12-13］.

（1）余弦相似性为

对于User-Based CF而言，相似度

其中，Sim（u1，u2）表示用户u1和用户u2之间的相似度，Ru1i和Ru2i分别表示用户u1、用户u2对项目i的评分，Iu1u2表示用户u1和用户u2共同评分的项目集合，即Iu1u2＝｛i∈I|Ru1i≠0，Ru2i≠0｝（其中I表示所有项目的集合），向量u1、向量u2表示用户u1和用户u2在Iu1u2上的评分.

（2）皮尔逊相关系数为

对于User-Based CF而言，相似度

通过相似度公式可以得到用户间的相似度，根据相似度的大小从大到小排序，对于用户u1可以产生一个邻居集合N＝｛N1，N2，…，Nk｝，即N中的第一个用户N1与用户u1的相似度对于用户u1来说是最大的.

1.3 推荐生成

根据第1.2节中产生的邻居集合N＝｛N1，N2，…，Nk｝，可以计算出用户对所有项目的喜爱程度的预测值［9］

其中，Pu1i表示用户u1对未评分项目i的预测评分，表示用户u1对所有评分过的项目的平均评分，表示用户u2对所有评分过的项目的平均评分.

2 改进的相似度度量方法

2.1 改进分析

在传统User-Based CF中，公式（2）和公式（4）未考虑到用户对共同评价项目的评分所占的比重带来的影响.假设两个用户共同参与评价的项目有很多，这不一定能说明两个用户的爱好是一样的.因为如果这些被共同评价过的项目的评分都不高，那么只能说明这两个用户都不喜欢这些项目，若这样推荐给用户的项目就会有偏差.假设两个用户共同评分的项目不多，但是两个用户对共同评分项目的评分都很高，这些项目很有可能是用户所喜爱的，那么这两个用户的爱好有很大概率是很相似的.因此我们在相似度计算过程中需要考虑用户对共同评分项目的评分所占的比重，这样才有助于提高相似度计算的精度.

本论文对相似度的公式进行改进，提出加权余弦相似性方法和加权皮尔逊相关系数方法，具体描述如下.

步骤1 从矩阵R（m，n）中计算用户u1和用户u2对共同评价项目的评分总和：

步骤2 从矩阵R（m，n）中计算用户u1和用户u2对各自评分过的所有项目的评分总和：（Iu1表示用户u1所有评过分的项目集）；（Iu2表示用户u2所有评过分的项目集）.

步骤3 对公式（2）和公式（4）中用户相似度进行改进，改进后的相似度计算公式为

则经过加权后计算预测评分公式为

2.2 时间复杂度分析

3 实验结果及分析

3.1 数据集

本实验所采用的数据集是MovieLens_100k数据集［14］.MovieLens_100k数据集的评分制度是5分制，它包含了943个用户以及1682部电影，其中每个用户至少对20部以上的电影进行了评分.数据集的内容是用Table表示，共有4列：用户ID；物品ID；评分；时间戳.在该数据集中主要分成两部分：Base数据集和Test数据集.Base数据集是训练样本，通过对Base数据集进行训练，可以计算出用户对未评分项目的预测评分；而Test数据集则是用户对未评分项目的实际评分，通过对比预测评分和实际评分，可以直观地了解推荐精度.

3.2 评分标准MAE

在推荐算法实验中，通常通过计算平均绝对误差［15-16］（Mean Absolute Error，MAE）来表示推荐精度.如第3.1节，实验通过对训练样本Base数据集进行训练，计算用户对未评分项目i的预测评分pi，再根据Test数据集中对应的用户对项目i的实际评分Ri；通过计算预测评分和用户的实际评分之间的偏差的绝对值，以此来表示对未评分项目i的推荐精度，即越小，对未评分项目i的推荐精度越高，相反，越高，则说明对未评分项目i的推荐精度越低，偏差越大.假设集合P＝｛p1，p2，p3，…，pn｝代表用户对未评分项目的预测评分集合，集合R＝｛R1，R2，R3，…，Rn｝代表用户对未评分项目的实际评分集合，则定义MAE为

根据公式（9）可以发现，MAE值越小即偏差越小，代表预测评分越准确，推荐精度越高.

3.3 实验结果及分析

为了验证本文提出的加权相似性度量的有效性，设计将其与传统User-Based CF进行比较.

3.3.1 验证相似度度量改进的有效性

首先，我们采用Movie Lens数据集中的训练数据集u1.base与测试集u1.test进行对比实验.通过对u1.base进行训练，从而预测用户对尚未评价项目的评分，将预测结果与u1.test中数据进行比较，最终得出MAE实验结果，如图1、图2所示.

图1 余弦相似度改进对比图Fig.1 The improvement of cosine similarity

在图1、图2中蓝色曲线是原算法的实验结果，红色曲线是采用改进后的相似度公式产生的实验结果，曲线上的点的横坐标代表邻居数k，纵坐标代表在对应邻居数k的情况下所得到的MAE.如图2中蓝色曲线的第一个点表示当邻居数k＝5时，MAE接近0.82，即预测评分的平均绝对误差接近0.82；而在图2中可以发现在采用改进后的相似度公式的情况下（即图2中红色曲线表示的那部分），当k＝5时，MAE约为0.78，很明显要小于采用原公式的平均误差.

图2 皮尔逊相似度改进对比图Fig.2 The improvement of Pearson similarity

在本文第2.1节中提到过，通过对原相似度公式进行加权计算，将用户对共同评价项目的评分所占的比重这个重要因素考虑在内，可以有助于提高精确度；而且通过对图1、图2的分析，我们发现本文中对相似度度量方法的改进是有明显效果的，在不同邻居数目的情况下，MAE都要小于传统算法，可见公式（6）和公式（7）能够有效地提高推荐精度，降低预测评分偏差.

3.3.2 邻居数k的选择

本次实验采用的数据集是MovieLens数据集中的u1，u2，u3，u4，u5，u6，u7，采用改进后的相似度度量公式（7），实验结果如图3所示.

图3 不同邻居数k的实验结果Fig.3 The experiment results caused by different number of neighbors

当最近邻居数k很小时，如果邻居集合N中有一些和用户爱好存在差别，那么预测评分的误差会偏大；但当最近邻居数k很大时，会带入很多与用户爱好有较大偏差的其他用户，从而会导致推荐精度降低，使MAE偏大，所以函数MAE-邻居数k应该存在最小值［8］.由图3中可知，针对改进后的算法，当最近邻居数k属于（40，60）时，MAE最小，推荐精度最高.

4 总 结

在如今信息化高速发展的时代，推荐系统帮助人们处理了很多干扰信息，将有效信息及时推荐给用户.推荐系统作为一个仍在不断发展和完善的技术，任何一个细小的问题都值得研究.推荐系统中最常用的算法就是协同过滤算法，但很多现有的改进算法没有对相似性度量进行分析.考虑到用户和项目之间的联系，本文通过对相似性度量的加权处理，有效降低了预测偏差，提高了推荐精度.

每个用户都有自己的爱好，每个项目也有各自的属性，如何将用户的爱好和项目的属性联系起来是今后研究的课题.另外，对于协同过滤算法的研究还有其他的思路，比如说结合User-based和Item-based的协同过滤算法、聚类算法等；如何结合各种思路的优点也是今后研究的课题之一.

［1］刘建国，周涛，汪秉红.个性化推荐系统的研究发展［J］.自然科学进展，2009，19（1）：1-15.

［2］孟祥武，纪威宇，张玉洁.大数据环境下的推荐系统［J］.北京邮电大学学报，2015，38（2）：1-15.

［3］硕良勋，柴变芳，张新东.基于改进最近邻的协同过滤推荐算法［J］.计算机工程与应用，2015，51（5）：137-141.

［4］ZHAO Z D，SHANG M S.User-based collaborative-filtering recommendation algorithms on Hadoop［C］／／Proceedings of the 2010 3rd International Conference on Knowledge Discovery and Data Mining.IEEE，2010：478-481.

［5］邓爱林，朱扬勇，施伯乐.基于项目评分预测的协同过滤推荐算法［J］.软件学报，2003，114（9）：1621-1628.

［6］彭玉，程小平，徐艺萍.一种改进的Item-based协同过滤推荐算法［J］.西南大学学报（自然科学版），2007，29（5）：146-149.

［7］刘芳先，宋顺林.改进的协同过滤推荐算法［J］.计算机工程与应用，2011，47（8）：72-75.

［8］汪静，印鉴，郑利荣，等.基于共同评分和相似性权重的协同过滤推荐算法［J］.计算机科学，2010，37（2）：99-104.

［9］ADOMAVICIUS G，TUZHILIN A.Toward the next generation of recommender systems：A survey of the stateof-the-art and possible extensions［J］.IEEE Transactions on Knowledge and Data Engineering，2015，17（6）：734-749.

［10］孟庆庆，张胜男，卢楚雍.基于用户特征和商品特征的组合协同过滤算法［J］.软件导刊，2015，14（3）：41-43.

［11］孙辉，马跃，杨海波，等.一种相似度改进的用户聚类协同过滤推荐算法［J］.小型微型计算机系统，2014，35（9）：1967-1970.

［12］傅鹤岗，彭晋.基于模范用户的改进协同过滤算法［J］.计算机工程，2011，37（3）：70-74.

［13］王立印，张辉，陈勇.一种基于Dice-Euclidean相似度计算的协同过滤算法［J］.计算机应用研究，2015，32（10）：2891-2895.

［14］朱毅萌，谢颖华.分步筛选邻居的协同过滤改进算法［J］.计算机系统应用，2015，24（6）：132-137.

［15］张丙奇.基于领域知识的个性化推荐算法研究［J］.计算机工程，2005，31（21）：7-9.

［16］蔡淑琴，袁乾，周鹏，等.基于信息传播理论的微博协同过滤推荐模型［J］.系统工程理论与实践，2015，35（5）：1267-1275.

（责任编辑：李 艺）

Improved collaborative filtering algorithm based on user-similarity

WANG Wei， ZHENG Jun
（Computer Center，East China Normal University，Shanghai 200062，China）

Collaborative filtering is widely accepted and applied currently as one of the most popular personalized recommendation methods.It is an implementation method based on content that has considerable advantages in accuracy.The core issue of collaborative filtering is how to work out the calculation of similarity.In this paper，we introduce the traditional collaborative filtering algorithm and make similarity calculation more accurately by optimizing the traditional formula of similarity.Experimental results show that the optimized algorithm can improve the accuracy of the recommendation and reduce the MAE（Mean Absolute Error，MAE）efficiently.

recommendation methods；similarity；collaborative filtering；MAE

TP391

A

10.3969／j.issn.1000-5641.2016.03.007

1000-5641（2016）03-0060-07

2015-05

国家高技术研究发展计划（2013AA01A211）

王 威，男，硕士研究生，主要研究方向为Web开发及应用.E-mail：610151625@qq.com.通信作者：郑 骏，男，教授，主要研究方向为Web开发及应用.E-mail：jzheng@cc.ecnu.edu.cn.