具有年龄结构的捕食被捕分食支系统的Bogdanov-Takens

刘霞,焦建锋

(河南师范大学数学与信息科学学院大数据统计分析与优化控制河南省工程实验室,河南新乡453007)

具有年龄结构的捕食被捕分食支系统的Bogdanov-Takens

刘霞,焦建锋

(河南师范大学数学与信息科学学院大数据统计分析与优化控制河南省工程实验室,河南新乡453007)

本文考虑了一类具有常值收获和年龄结构的捕食被捕食系统的Bogdanov-Takens (BT)分支问题.给出了系统的正平衡点是BT奇点的充分条件以及系统在该奇点处的开拆标准型,从而得出在该平衡点附近处会出现的分支现象.

时滞;捕食被捕食系统;Bogdanov-Takens(BT)分支;年龄结构

0 引言

年龄结构类型的时滞捕食被捕食系统的局部稳定的性质、Hop f分支的存在性及Hop f分支的方向及稳定性已经被一些作者研究[1-2].文献[2]考虑了一类带两个时滞的捕食者是如下比率依赖型的捕食被捕食系统：

其中x(t)表示被捕食者在时间t时的种群密度,y1(t)和y2(t)分别表示不成熟和成熟的捕食者在时刻t时的种群密度.参数r,r1,r2,k,a1,a2,m,d1均为正常数,它们的生物学意义详见文献[2].

对于种群间动力学行为更加深入的研究以及一些带收获和不同的功能反应函数的捕食被捕食模型被研究可参见文献[3]—[6].根据文献[6]—[8]的思想,把常数收获项合并到系统(0.1)中,可以获得如下系统：

其中x(t)表示被捕食者在时间t时的种群密度,y1(t)和y2(t)分别表示不成熟和成熟的捕食者在时刻t时的种群密度.所有的参数均为正常数,且k表示被捕食者的环境容纳量,代表被捕食者的常数率收获,其他的参数和系统(0.1)中的参数具有相同的生物学意义.为了简便,我们取系统(0.1)中的时滞τ2=τ1.为了计算的简洁,首先要化简系统(0.2).

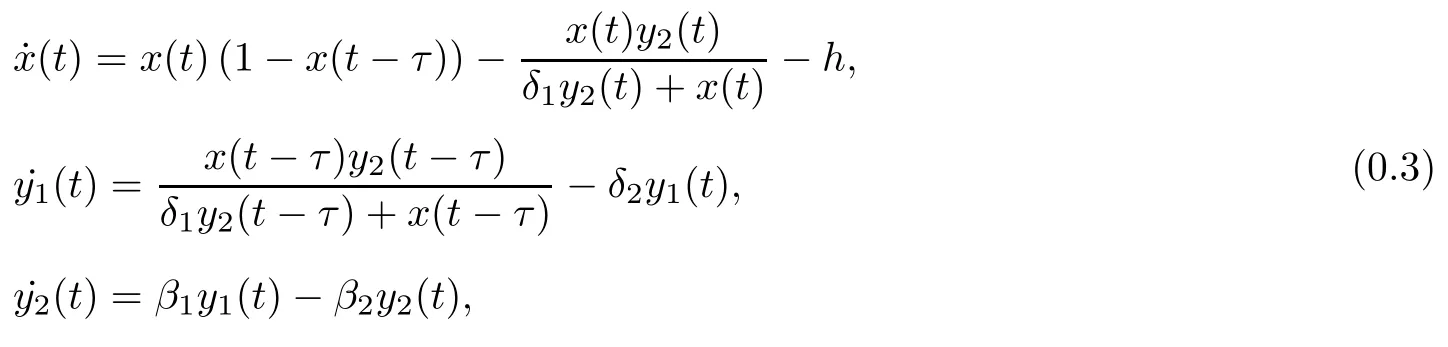
系统(0.3)的初值条件为

本文的具体结构如下：第1部分,主要讨论了BT奇点的存在性;第2部分,推导出了系统在BT奇点处的规范型;第3部分,对所获得的理论结果进行数值模拟.

1 BT奇点的存在性

为了研究系统(0.3)的退化性质,我们需要计算满足方程x2δ1β1+(β1-δ2β2-δ1β1)x+ hδ1β1=0的退化平衡点.容易计算系统(0.3)有一个退化平衡点,如果

对方程(1.3),如果F(0)=F′(0)=0,F′′(0)/=0成立,则可以得到如下的引理.

引理1.1令(H1)((1.1)和成立,则λ=0是方程(1.3)的2重根.

在条件(H1)下,还需要考虑方程(1.3)的其他特征根具有非零实部.由于这个问题的解决十分困难,所以我们通过证明方程(1.3)没有纯虚根来获得非零实特征根存在性的一个充分条件.在方程(1.3)两边同时乘以eλτ,得到

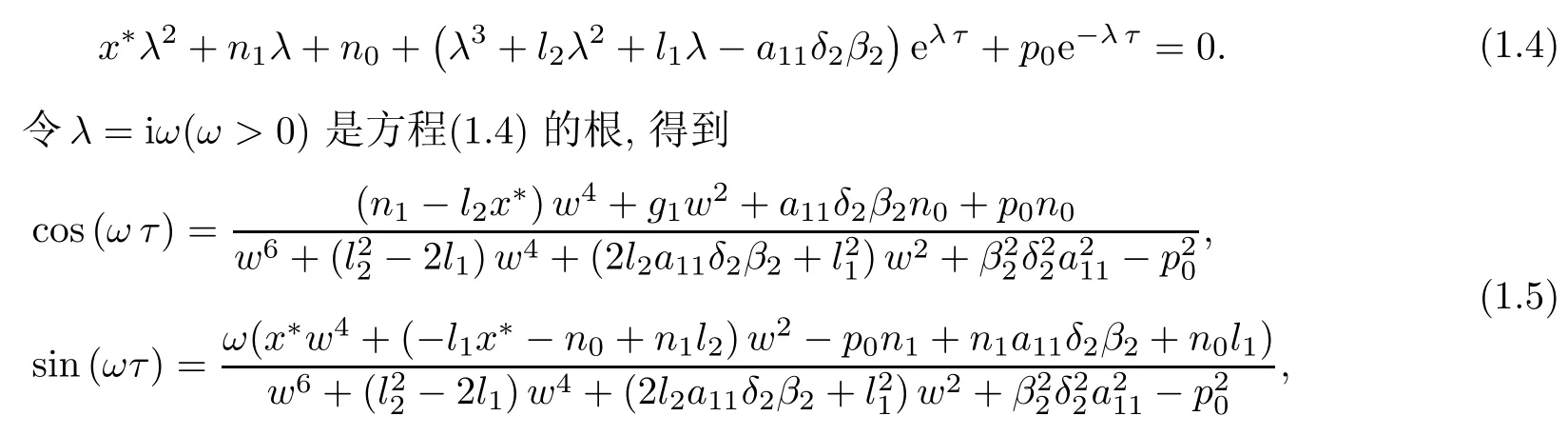
其中g1=l2n0-n1l1-a11δ2β2x*-p0x*.

从(1.5)得到方程

其中

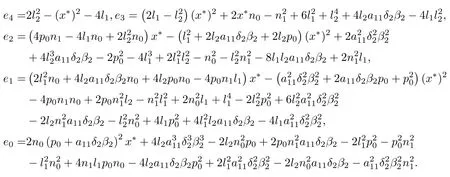
如果方程(1.6)没有正根,则方程(1.3)的其他特征根具有非零实部.因此,有以下的定理.

定理1.1令(H1)成立,且方程(1.6)无正根,则系统(0.3)的平衡点E*是一个BT奇点.

例如,对系统(0.3),我们取δ1=5,δ2=0.2,β1=0.1,β2=0.2,则x*=0.44,,h0=0.193 6,τ0≈0.384 615 384 6,这时,方程(1.6)无正根.因此,定理1.1的所有条件可以得到满足.

2 BT分支的规范型

在这一部分,取h=h0和τ=τ0作为分支参数来讨论系统(0.3)在平衡点E*处的动力学现象.令h=h0+µ1和τ=τ0+µ2,为了计算的简便,我们把系统(0.3)写作

其中(µ1,µ2)在原点处充分小.在系统(2.1)中,对于原点附近任意的µ1和µ2,容易看出E*不是平衡点.通过使用和文献[6]相似的思路,如果我们想得到系统(0.3)在平衡点E*处BT分支的规范型,需要把微分方程˙µ1=0增加到系统(2.1)中.因此,接下来需要去推导四维系统的三重分支,该四维系统可以表示如下

其中,“h.o.t.”是“higher order term”的缩写,表示高阶项,zt=(x(t),y1(t),y2(t),µ1)T,z(t+θ)=ϕ(θ),ϕ=(ϕ1,ϕ2,ϕ3,µ1)T∈C4,

系统(2.2)的在原点处的线性化系统为

线性系统对应的特征矩阵为

为了得到系统(2.1)在平衡点E*处的规范型,需要计算Φ(θ),它是系统广义特征空间P的一个基.根据文献[9],Φ(θ)选择如下

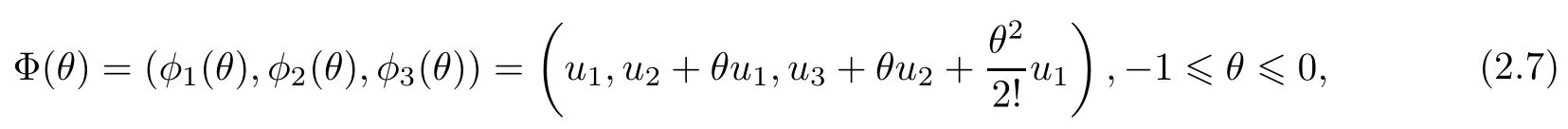
其中u1,u2,u3是下面线性方程组的解：

解方程组(2.8)得

其中

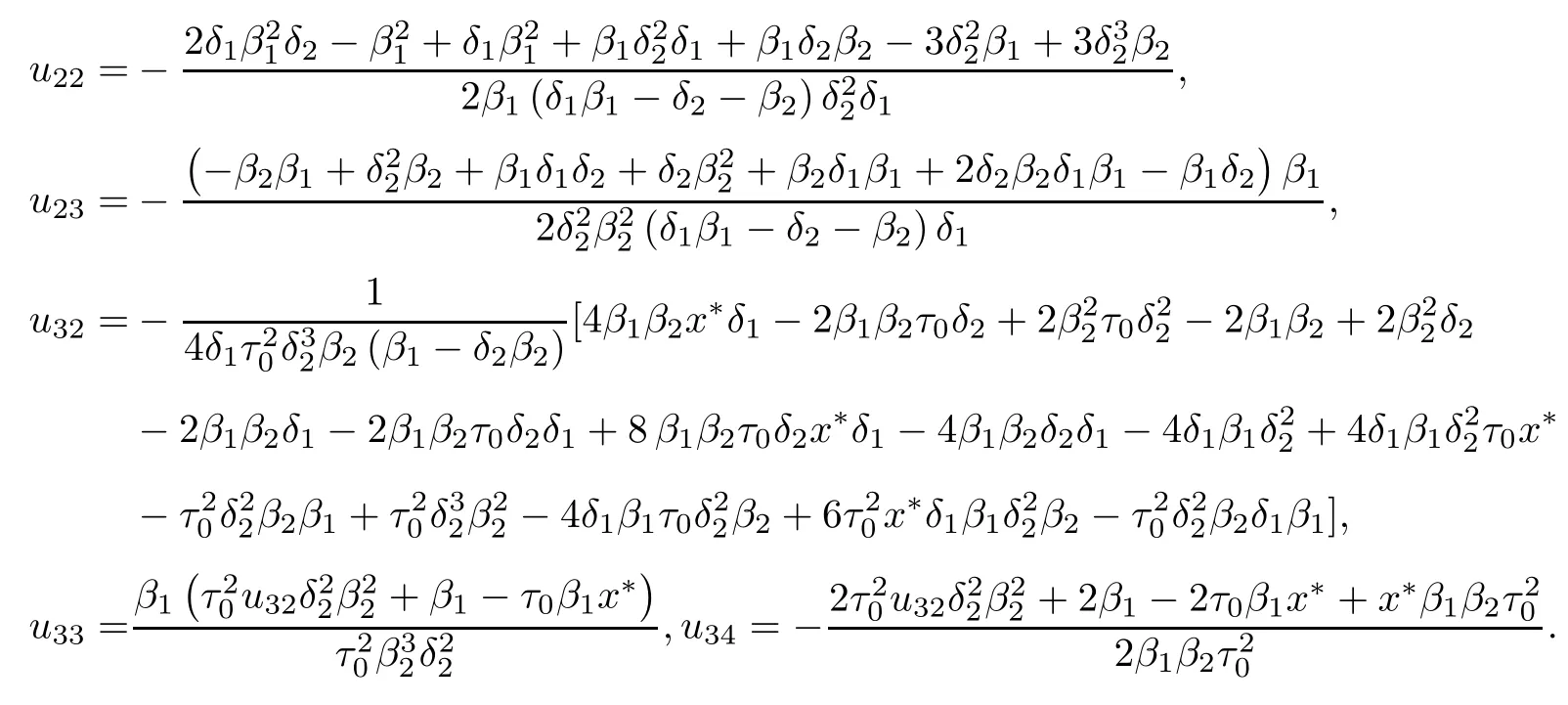
P的对偶空间P*的基Ψ(s)选择如下

其中“col”表示矩阵里的向量ψ1,ψ2,ψ3按列排,且v3,v2,v1是下面线性方程组的解：

从方程(2.11)得到

然后,由(2.4),(2.7)和(2.10)式,得到

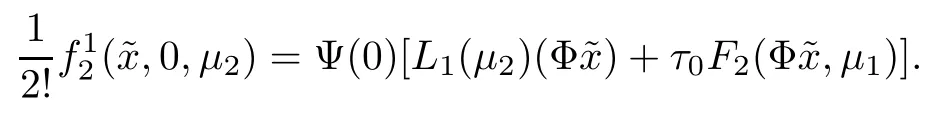
由(2.14)—(2.15)和(2.17),得

此外,由(2.14)式得

其中ϵ1=-A2γ1,ϵ2=γ2.由参考文献[4,11]的结果,我们得到下面的定理.

定理2.1令(H1)成立,且方程(1.6)无正根,则(2.20)出现如下的分支：(i)鞍结点分支曲线SN={(µ1,µ2)：ϵ1=0,ϵ2/=0};(ii)Hop f分支曲线H={(µ1,µ2)：; (iii)同宿分支曲线HL={(µ1,µ2)：,ϵ2＞0}.

3 数值模拟

在这一部分,我们利用数值模拟的办法去验证以上所研究的理论结果,并且画出了系统的分支图.对于系统(0.3),取δ1=5,δ2=0.2,β1=0.1,β2=0.2,则x*=0.44,,,h0=0.193 6,τ0≈0.384 615 384 6,方程(1.6)没有正根.定理2.1的条件得以满足,所以系统(2.1)在正平衡点E*处的规范型是系统(2.20).由定理2.1,我们可以得到在扰动变量µ1,µ2平面上相应的分支图(参看图1).µ1-µ2平面上,BT分支点附近的小邻域被鞍结点分支曲线SN,Hopf分支曲线H以及同宿分支曲线HL分成4个不同的动力系统区域I,II,III,IV.因此,由定理2.1,我们可以得到图1.

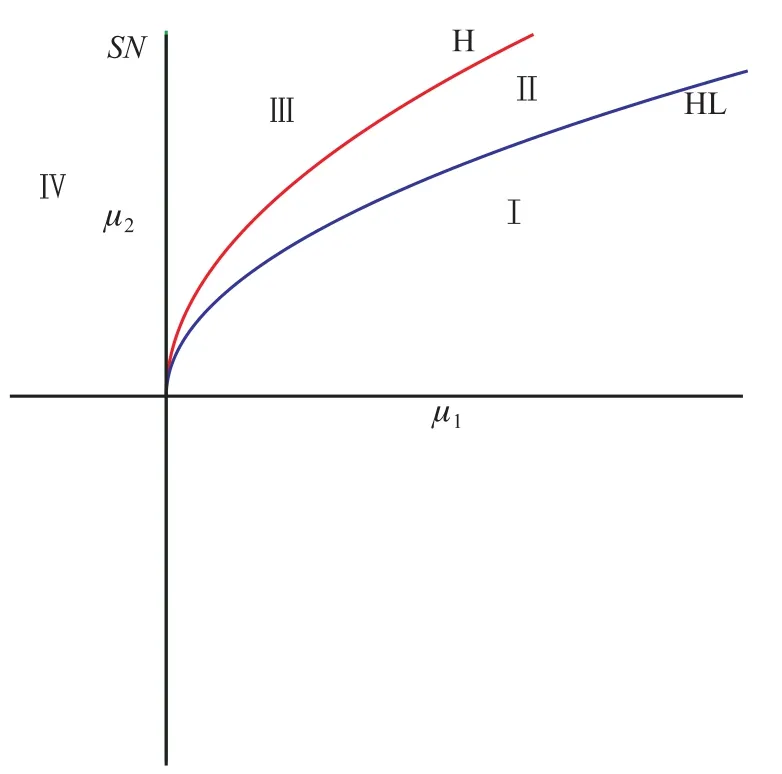
图1 系统(2.20)在μ1-μ2平面上的分支图Fig.1 Bifurcation diagram of system(2.20)in theμ1-μ2p lane

[1]XU R.Global stability and Hopf bifurcation of a predator-prey model with stage structure and delayed predator response[J].Non linear Dyn,2012,67：1683-1693.

[2]DENG L W,WANG X D,PENG M.Hopf bifurcation analysis for a ratio-dependent predator-prey system with two delays and stage structure for the predator[J].Applied Mathematics and Computation,2014,231：214-230.

[3]WANG L,FAN Y,LI W.Multiple bifurcations in a predator-prey system with monotonic functional response [J].Applied Mathematics and Computation,2006,172：1103-1120.

[4]XIAO D M,RUAN S G.Multiple bifurcation in a delayed predator-prey system with nonmonotonic functional response[J].Journal of Differential Equations,2001,176：494-510.

[5]XIA J,LIU Z,YUAN R,et al.The effects of harvesting and time delay on predator-prey systems with Holling type II functional response[J].SIAM J Appl Math,2009,70：1178-1200.

[6]JIANG J,SONG Y L.Delay-induced Bogdanov-Takens bifurcation in a Leslie-Gower predator-prey model with nonmonotonic functional response[J].Commun Nonlinear Sci Numer Simulat,2014,19：2454-2465.

[7]CAMPBELL S A,YUAN Y.Zero singularities of codimension two and three in delay differential equations[J]. Non linearity,2008,21：2671-2691.

[8]GUO S J,MAN J J.Center manifolds theorem for parameterized delay differential equations with applications to zero singularities[J].Non linear Analysis,2011,74：4418-4432.

[9]QIAO Z Q,LIU X B,ZHU D M.Bifurcation in delay differential systems with triple-zero singularity[J].Chinese Ann Math Ser A,2010,31：59-70.

[10]FARIA T,MAGALH˜AES L T.Normal forms for retarded functional differential equations and applications to Bogdanov-Takens singularity[J].Journal of Differential Equations,1995,122：201-224.

[11]CHOW S N,LI C Z,WANG D.Normal Forms and Bifurcation of Planar Vector Field s[M].Cambridge：Cambridge University Press,1994.

(责任编辑：林磊)

Bogdanov-Takens bifurcation for a delayed predator prey system with stage structure

LIU Xia,JIAO Jian-feng
(Big Data Statistical Analysis and Optimization Control Engineering Laboratory in Henan Province, College of Mathematics and Information Science,Henan Normal University, Xinxiang Henan 453007,China)

In this paper the Bogdanov-Takens(BT)bifurcation of a delayed predator prey system with stage structure and constant harvesting is considered.The existing conditions which guarantee an interior equilibrium of the system is BT singularity are obtained and the corresponding normal form for the system at this singularity is p resented, some bifurcation results are shown.

delay;predator prey system;Bogdanov-Takens bifurcation;stage structure

O 175.1

A

10.3969/j.issn.1000-5641.2016.03.005

1000-5641(2016)03-0039-09

2015-06

河南省教育厅科学技术研究重点项目(14A 110019,15A 110034);河南师范大学校级骨干教师项目资助

刘霞,女,副教授,硕士生导师,研究方向为生物数学.E-mail：liuxiapost@163.com.