一类结构张量方程解集的非空紧性

侯 印，凌 晨

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

张量方程是矩阵方程的自然推广，在许多工程和科学计算领域有广泛应用，例如数据挖掘[1]、数值偏微分方程[2]和张量互补问题[3]等。与矩阵方程相比，高阶张量的出现导致张量方程中的相关函数呈高次特性。此时，张量方程解的存在性和有效数值算法设计均需针对所涉及的张量结构进行研究和设计。在系数张量为非奇异M-张量和正常数向量(即每一分量均为正实数)的情形时，已经证明张量方程存在唯一正解[2]，并利用张量结构性质设计出许多有效算法用于求此正解[4-5]。但是，许多应用问题中的张量方程并不具有M-张量特性，从而需要进一步研究张量方程解的存在性并设计有效数值算法来求解。本文专注于研究系数张量为强H-张量时方程解的非空紧性，为进一步设计有效算法打下理论基础。

1 问题描述

考虑如下形式的张量方程问题(简记为TEs)，即求x=(x1,x2,…,xn)T∈Rn，使得

Axm-1=b

(1)

式中，A=(ai1i2…im)1≤i1,i2,…,im≤n是m阶n维实系数张量(即对任意1≤i1,i2,…,im≤n，均有ai1i2…im∈R)，b=(b1,b2,…,bn)T∈Rn为常数向量，而Axm-1表示n维向量，其第i分量为

满足式(1)的x为张量方程的解，其全体记为SOL(A,b)。若SOL(A,0)={0}，则A是非奇异张量，否则A为奇异张量[6]。

B为非负张量(即B中的每一元素均非负)，则A为Z-张量。进一步，若c≥ρ(B)，则A为M-张量；若c>ρ(B)，则A为非奇异M-张量[9]。对给定的A∈Tm,n，M(A)=(mi1i2…im)是张量A的比较张量[9]，其元素为

显然，对A∈Tm,n，其比较张量M(A)必是Z-张量。基于M-张量和比较张量的概念，有如下H-张量的定义。

定义1[9]设A∈Tm,n。若M(A)为(非奇异)M-张量，则A为(强)H-张量。

显然，若A∈Tm,n是(非奇异)M-张量，则A必是(强)H-张量。下列例子说明，反之不成立。

本文首先证明当系数张量为强H-张量时，齐次张量方程(1)(即常数向量b=0)只有唯一零解；在此基础上，利用拓扑度理论证明，当系数张量为强H-张量和半正定时，非齐次张量方程(即常数向量b≠0)的解集为非空紧。

2 预备知识

首先介绍若干结构张量的定义和相关性质，然后引进拓扑度的概念及2个著名结论。

显然，若A∈Tm,n是严格对角占优张量，则A必是拟严格对角占优张量。但下列例子说明，反之不成立。

表明A是拟严格对角占优张量。

引理1[9]设A∈Tm,n。则A是强H-张量，当且仅当A是拟严格对角占优张量。

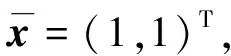
下面给出2个重要引理。

deg(G,D,y)=deg(F,D,y)，

其中H(t,x)=tG(x)+(1-t)F(x)和0≤t≤1。

引理3[14]设F:Rn→Rn是连续函数，b∈Rn且D是Rn中有界开集，若deg(F,D,b)≠0，则F(x)=b在D上必有一解。

在给出使得deg(G,Br,0)≠0(其中G(x)=Axm-1，A∈Tm,n,m≥3)成立的一个充分条件前，先引入如下定义。

定义4[12]设A∈Tm,n。若存在λ∈R和x∈Rn，使得

则λ为A的Z特征值，x为A的对应于λ的Z特征向量。

条件1设A∈Tm,n，A所有的Z特征值为正。

下面的例子表明，满足条件1的张量A是存在的。

(2)

3 解集的非空紧性

本节讨论系数张量为强H-张量时，式(1)解集的非空紧性。首先讨论b=0的情形。

引理4设A∈Tm,n。若A为严格对角占优张量，则A为非奇异张量。

定理1设A∈Tm,n。若A为强H-张量，则A为非奇异张量。

(3)

其次讨论b≠0的情形。先给出如下命题。

命题1设A∈Tm,n。若A为半正定的强H-张量，则A满足条件1。

下面的例子表明，半正定的强H-张量存在，且未必是正定的(而m=2时，半正定的强H-矩阵必是正定的)。

(4)

给出主要定理，它表明在系数张量为半正定强H-张量的条件下，张量方程的解集是非空紧的。

定理3设A∈Tm,n。若A为半正定的强H-张量，则对任意b∈Rn，SOL(A,b)是非空紧集。

H(t,x)=tG(x)+(1-t)P(x)，∀(t,x)∈[0,1]×∂Br

分情况讨论：(a)若存在r>0，使得对任意(t,x)∈[0,1]×∂Br，都有H(t,x)≠0，则由引理2知，deg(P,Br,0)=deg(G,Br,0)≠0。从而由引理3知，Axm-1=b在Br内必有一解。(b)若对任意r>0，存在(tr,xr)∈[0,1]×∂Br，使得H(tr,xr)=0，即

(5)

μrA(xr)m-1=b

(6)

(7)

(8)

4 结束语

张量方程是值得研究的新问题。本文简要讨论了几类结构张量之间的关系。当张量方程中的系数张量为强H-张量时，证明了齐次张量方程只有唯一零解。在此基础上，进一步证明了系数张量为半正定的强H-张量时，非齐次张量方程解集是非空紧的。然而，因半正定张量必定是偶数阶的，所以本文定理3的结论仅在偶数阶情形时成立。人们自然会问：当张量阶数为奇数时，张量方程(1)解的存在性质如何？又当张量阶数为偶数时，定理3中的半正定性条件可否删除？这些均是值得进一步研究的问题。