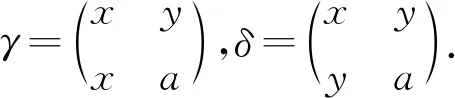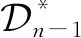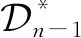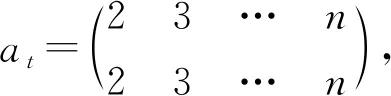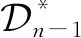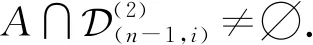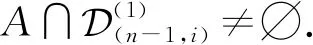部分一一保序扩张有限变换半群的生成元集

王 芳，杨秀良

(杭州师范大学理学院，浙江 杭州 311121)

1 引言和主要结果叙述

众所周知，每个有限逆半群都嵌入到某个有限对称逆半群[1].设In是有限集Xn={1,2,…,n}上的对称逆半群，它的逆子半群IOn={α∈In|∀x,y∈dom(α),x≤y⟹xα≤yα}最近引起了人们极大的关注[2-7]. 特别地，Al-Kharousi等[7]研究了IOn的保序等距子半群

ODPn={α∈IOn|∀x,y∈dom(α),|x-y|=|xα-yα|}∪{∅}

的生成元集和秩，且它为逆半群.本文将ODPn拓展到更大的IOn的子半群，即保序扩张和保序伸缩两个子半群:

OEXn={α∈IOn|∀x,y∈dom(α),|x-y| ≤|xα-yα|}∪{∅}，

OCOn={α∈IOn|∀x,y∈dom(α),|x-y|≥|xα-yα|}∪{∅}.

类A半群的定义见[8]，设A为半群S的一个生成元集，如果对任意a∈A，A{a}不能生成S，则称A为半群S的一个极小生成元集.一个有限半群S的秩[7]定义为

rank(S)=min{|A|∶A⊂S,〈A〉=S}.

本文的主要结果如下：

定理1半群OEXn是一个非正则类A半群，ODPn是OEXn的最大逆子半群.

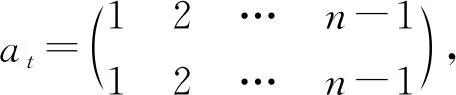
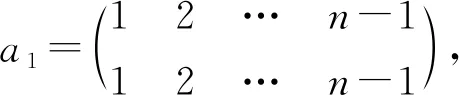
定理2OEXn任一个极小生成元集为

其中，γX表示X中的元，

且rank(OEXn)=2n-1.

2 主要结果的证明

Green-关系的定义见[1].设α∈OEXn，dom(α)和im(α)依次表示α的定义域和值域.

引理1设α，β∈OEXn，则

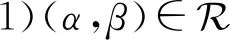
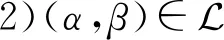
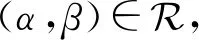
现任取x，y∈A，于是|xα-yα|≤|(xα)δ1-(yα)δ1|=|xβ-yβ|，且 |xβ-yβ|≤|(xβ)γ1-(yβ)γ1|=|xα-yα|.故|xα-yα|=|xβ-yβ|.

又因α,β∈OEXn，于是任取x,y∈A有x≤y⟹xα≤yα,xβ≤yβ.因此xα-yα=xβ-yβ.

综上，得dom(α)=dom(β)=A，且对任意x，y∈A，xα-yα=xβ-yβ.

“⟸”.设dom(α)=dom(β)=A，且对任意x，y∈A，xα-yα=xβ-yβ，可令

则ai-aj=bi-bj且xi≤xj⟹ai≤aj,bi≤bj(∀i,j∈{1,2,…,k})，从而ai≤aj⟹bi≤bj，bi≤bj⟹ai≤aj(∀i,j∈{1,2,…,k}).现令

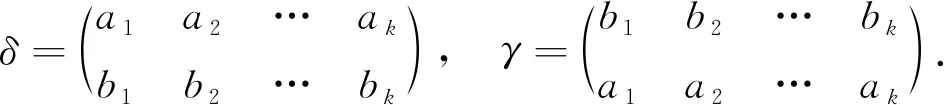
现任取x，y∈B，于是由(xα-1)γ2β=x且(yα-1)γ2β=y得(xα-1)γ2=xβ-1且(yα-1)γ2=yβ-1.从而

|xα-1-yα-1|≤|(xα-1)γ2-(yα-1)γ2|=|xβ-1-yβ-1|.

又由(xβ-1)δ2α=x且(yβ-1)δ2α=y得(xβ-1)δ2=xα-1且(yβ-1)δ2=yα-1.从而

|xβ-1-yβ-1|≤|(xβ-1)δ2-(yβ-1)δ2|=|xα-1-yα-1|.

故|xα-1-yα-1|=|xβ-1-yβ-1|.

又因γ2∈OEXn，于是任取x,y∈B有xα-1≤yα-1⟹(xα-1)γ2≤(yα-1)γ2⟹xβ-1≤yβ-1.因此xα-1-yα-1=xβ-1-yβ-1.

综上,得im(α)=im(β)=B，且对任意x，y∈B，xα-1-yα-1=xβ-1-yβ-1.

“⟸”.设im(α)=im(β)=B，且对任意x，y∈B，xα-1-yα-1=xβ-1-yβ-1，可令

则ai-aj=bi-bj且ai≤aj⟹yi≤yj,bi≤bj⟹yi≤yj(∀i,j∈{1,2,…,k})，从而ai≤aj⟹bi≤bj，bi≤bj⟹ai≤aj(∀i,j∈{1,2,…,k}).令

xi-xj=yi-yj，yiβ-yjβ=xiα-xjα(∀i,j∈{1,2,…,k}).

故|dom(α)|=|dom(β)|=k，且设dom(α)={x1,x2,…,xk}，存在排序dom(β)={y1,y2,…,yk}使

xi-xj=yi-yj，yiβ-yjβ=xiα-xjα(∀i，j∈{1,2,…,k}).

“⟸”.设|dom(α)|=|dom(β)|=k，且dom(α)={x1,x2,…,xk}，存在排序dom(β)={y1,y2,…,yk}使

xi-xj=yi-yj，yiβ-yjβ=xiα-xjα(∀i，j∈{1,2,…,k}).

从而任取xi,xj∈dom(α),yi,yj∈dom(β)有yi≤yj⟹xi≤xj⟹xiα≤xjα且|yi-yj|=|xi-xj|≤|xiα-xjα|(∀i，j∈{1,2,…,k}).

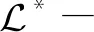
引理2设α，β∈OEXn，则

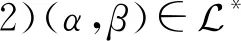
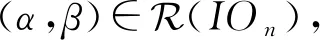
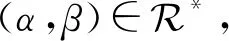
因此dom(α)=dom(β).

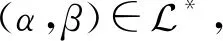
因此im(α)=im(β).

□

引理3设α，β∈OEXn，

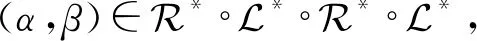
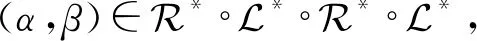
从而由引理2得

|im(α)|=|im(δ1)|，im(δ1)=im(δ2)，|im(δ2)|=|im(δ3)|，im(δ3)=im(β).

故|im(α)|=|im(β)|.

从而由引理2得

im(α)=im(γ1)，|im(γ1)|=|im(γ2)|，im(γ2)=im(γ3)，|im(γ3)|=|im(β)|.

故|im(α)|=|im(β)|.

□

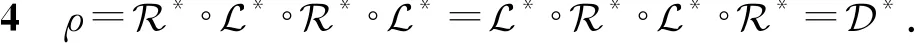
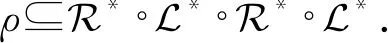
其中|xi-xj|≤|ai-aj|,|yi-yj|≤|bi-bj|且xi≤xj⟹ai≤aj,yi≤yj⟹bi≤bj(∀i,j∈{1,2,…,k}且i≤j).

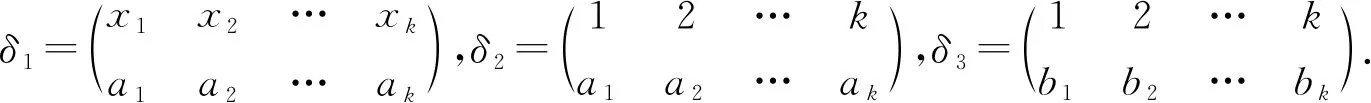
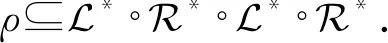
其中|xi-xj|≤|ai-aj|,|yi-yj|≤|bi-bj|且xi≤xj⟹ai≤aj,yi≤yj⟹bi≤bj(∀i,j∈{1,2,…,k}且i≤j).

□

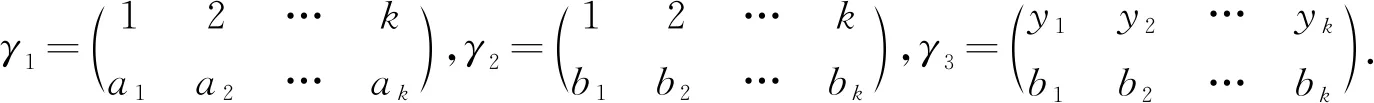
引理5α∈OEXn为正则元当且仅当α∈ODPn.

证明“⟸”.若α∈ODPn，则α是逆元，从而α是正则元.又因ODPn⊆OEXn，故α是OEXn的正则元.

“⟹”.若α∈OEXn是正则元，则存在β∈OEXn使αβα=α.于是，任意x∈dom(α)，有xαβ=(xαβα)α-1=xαα-1=x.现任意x,y∈dom(α)，有

|x-y|≤|xα-yα|≤|(xα)β-(yα)β|=|x-y|.

从而|xα-yα|=|x-y|.又由α∈OEXn，则α∈IOn，故α∈ODPn.

□

定理1的证明先证半群OEXn是一个类A半群.

易知E(OEXn)是一个半格，于是有OEXn是一个适当半群.

任取α∈OEXn，ε是OEXn的任意幂等元，则ε是恒等映射，现定义φε,α∈OEXn为

(x)φε,α=x(∀x∈im(εα))，dom(φε,α)=im(εα).

接下来定义φα,ε∈OEXn为

(x)φα,ε=x(∀x∈dom(αε))，dom(φα,ε)=dom(αε).

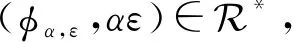
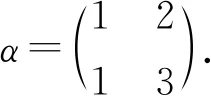
最后证ODPn是OEXn的最大逆子半群.从[7]知ODPn是OEXn的逆子半群.任取S是OEXn的一个逆子半群且满足ODPn⊆S⊆OEXn.现任取α∈S，则α是可逆的，从而α是一个正则元，进而由引理5可得α∈ODPn.故S⊆ODPn.因此S=ODPn，即ODPn是OEXn的最大逆子半群.

□

以下探讨OEXn的任一个极小生成元集.

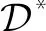
(4)n-1=12…n-112…n-1 12…n-123…n 23…n12…n-1 23…n23…n .

对i∈{2,3,…,n-1}，令

(2)(n-1,i)=1…i-1ii+1…n-11…i-1i+1i+2…n 2…ii+1…n1…i-1i+1…n .

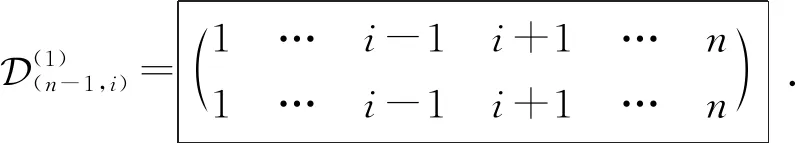
(1)(n-1,i)=1…i-1i+1…n1…i-1i+1…n .

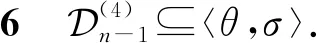
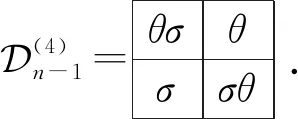
(4)n-1=θσθσσθ .

结论成立.

□

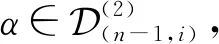
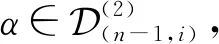
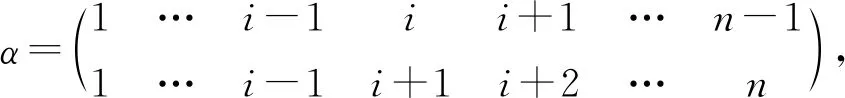
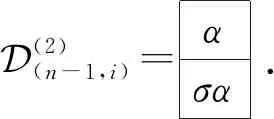
(2)(n-1,i)=ασα .

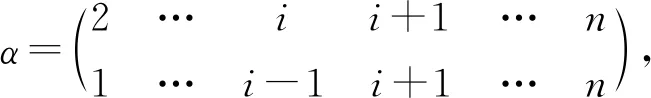
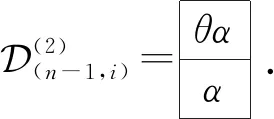
(2)(n-1,i)=θαα .

综上，结论成立.

□

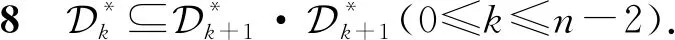
证明当k=0 时，显然结论成立.对k≤n-2，有n-k≥2.下对k≥1分情况讨论.

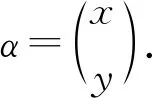
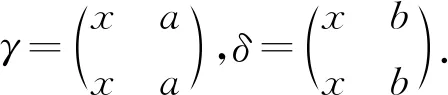
情况2当x

情形1 若y-x=1，则存在元a∈Xn使ay.

情况3当x>y时，可仿照情况2的证明过程，结论成立.

情况1若存在y∈Xn使xi

显然β,γ∈OEXn且计算可得α=βγ.

情况2若xi+1-xi=1(i∈{1,2,…,k-1})，dom(α)分3种情形讨论.

情形1 若xn=n，即dom(α)={n-k+1,n-k+2,…,n}.存在元b∈Xnim(α)，不妨设ai

显然β,γ∈OEXn且计算可得α=βγ.

情形2 若x1=1，即dom(α)={1,2,…,k}.存在元b∈Xnim(α)，不妨设ai

显然β,γ∈OEXn且计算可得α=βγ.

情形3 若x1≠1且xk≠n.证明同情形1或者情形2的证明过程.

□

引理9A是OEXn的任意生成元集，则

1)ε,θ,σ∈A；

证明1)由推论1知ε∈A，且易知任取a∈A都有aε=εa=a.下证θ,σ∈A.

2)在以下证明中出现的i，都表示为i∈{2,3,4,…,n-1}.

□

定理2的证明由引理6、7、8及推论1知

是OEXn的生成元集.由引理9得，任取α∈S，都有S{α}不是OEXn的生成元集，故S是OEXn的极小生成元集.又由引理9易知OEXn任一个极小生成元集为

且计算得rank(OEXn)=2n-1.

□