两个奇质数乘积长度的二元二次剩余码的幂等生成元

刘渊博, 廖群英

(四川师范大学 数学科学学院, 四川 成都 610066)

1 准备知识

二次剩余码是码率接近1/2的循环码,因其良好的性质被广泛地研究和应用.早在1958年,Prange[1]基于循环码的代数性质提出了有限域上码长为奇质数的二次剩余码的概念.二次剩余具有较大的最小距离,所以它有非常好的纠错能力[2-3],从而广泛应用于网络传输、卫星通信、信息储存以及图像的信息隐藏等技术[4-5].二次剩余码在理论方面有丰富的研究结果.特别地,其幂等生成元可用于研究最小距离下界和译码算法,所以成为最重要的研究问题之一[3,6-7].Macwilliams等[3,8]给出了有限域上码长为奇质数的二次剩余码的幂等生成元,进而在1978年又进一步研究了扩充二次剩余码的幂等生成元.2005年,Semyonovykh[9]将码长为奇质数的二元二次剩余码的概念推广到高次剩余码,考虑了三次和四次剩余码的幂等生成元.

近年来,有限域上码长为奇质数的二次剩余码有了进一步的推广,相应的幂等生成元也有丰富的结果.首先,在构造方法上,Charters[10]于2009年将经典的码长为奇质数的二元二次剩余码推广到p元域上的p次剩余码,并利用构造出的幂等生成元给出其中一些码的最小距离的下界,其中p为奇素数.另外,Zanten等[11]在2015年构造了有限域上码长为n的t次剩余码,并给出了这些码的幂等生成元,其中t为大于1的正整数,n∈{2,4,pλ,2pλ|λ≥1}.其次,在码长方面,Ding[12]在2012年构造了有限域Fl上码长为n=pq的二次剩余码.特别地,得到二元二次剩余码、三元二次剩余码以及四元二次剩余码的具体构造,而且进一步得到这些码的最小odd-like权重的下界,其中p、q为奇质数且勒让德符号[5]

2 相关引理

d=

故可记C=[n,k,d]l.特别地,若线性码C满足:对任意c=(c0,c1,…,cn-1)∈C,C的循环移位(cn-1,c0,c1,…,cn-2)∈C,则称C为循环码.循环码作为一类特殊的线性码,有非常好的代数结构,因任意码字c=(c0,c1,…,cn-1)可写成多项式

c(x)=c0+c1x+…+cn-1xn-1∈

R=Fl[x]/(xn-1).

degg(x)≤n-1,

引理 2.1[6]设f(x)∈Fl[x]且循环码C=〈g(x)〉,则f(x)是C的生成元当且仅当

gcd(f(x),xn-1)=g(x).

特别地,若C=〈e(x)〉且在R中e2(x)=e(x),则称e(x)为C的幂等生成元.

取l=2,设n=pq,其中p,q为两个不同的奇质数,θ是Ω2中的n次本原单位根.

A0={i|gcd(i,n)=1,i∈A},

A1={i|gcd(i,n)=p,i∈A},

A2={i|gcd(i,n)=q,i∈A},

则

x

A},

A},

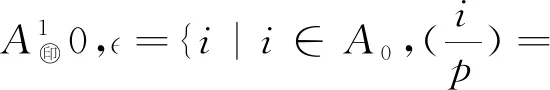
则

最后,对j,m∈{1,2},设

Fj=±1,

(1)

以及

Fm0=±1,

(2)

则以下有两种分解

x

F1,-1(x)F2,1(x)F2,-1(x)

或

x

F1,-1(x)F2,1(x)F2,-1(x).

定义 2.1[12]设p,q≡±1 (mod8).对0,1,2∈{1,-1}以及m=1,2,称循环码

C=〈Fm0,0(x)F1,1(x)F2,2(x)〉

或

C=〈(x-1)Fm0,0(x)F1,1(x)F2,2(x)〉

为二元二次剩余码.

注 2.1当m=1,2时,分别为文献[12]的第二、三种构造,且这样的二元二次剩余码共有32个.

对j,m∈{1,2},设

Ej=±1,

以及

E0=±1.

记

Em0,1,2(x)=Em0,0(x)+E1,1(x)+E2,2(x),

以及

gm0,1,2(x)=Fm0,0(x)F1,1(x)F2,2(x),

则

C=〈gm0,1,2(x)〉

或者

C=〈(x-1)gm0,1,2(x)〉,

即为定义2.1中的二元二次剩余码.

在讨论幂等生成元之前,先引入两个引理.

引理 2.2设p,q为不同的奇质数,θ为Ω2中的pq次本原单位根.对s∈{1,2,…,pq-1}及和E(θs)有如表1的结果.

表1 幂等元

证明要证明引理2.2,只需证明表1中第二列的情形其中s∈{1,2,…,pq-1},其他情形的证明类似.

2) 当s∈A1时

3) 当s∈A2时

这就完成了引理2.2的证明.

引理 2.3设p、q为不同的奇质数,θ为Ω2中的pq次本原单位根.若

E1,1(θ)=E2,1(θ)=0,

则

证明

这就完成了引理2.3的证明.

注 2.2在引理2.3中,满足

E1,1(θ)=E2,1(θ)=0

(E1,1(θ))2=E1,1(θ)

且

(E2,1(θ))2=E2,1(θ).

E1,1(θ)=a,E2,1(θ)=b,a,b∈{0,1}.

由中国剩余定理得,存在s∈A0满足

由引理2.1得

E1,1(θs)=E2,1(θs)=0.

3 二元二次剩余码的幂等生成元

下面给出定义2.1中相应的二元二次剩余码的幂等生成元.

定理 3.1对0,1,2∈{1,-1}以及m=1,2,则为幂等元且码

C=〈Em0,1,2(x)〉，

C的生成多项式与幂等生成元的对应关系如表2所示.

表2 二次剩余码的幂等生成元

其次,由定理3.1得到

的幂等生成元,即结论如下.

定理 3.2对设

4 定理的证明

定理 3.1的证明因为

q≡p≡±1 (mod8),

所以

E1,1(θ)=E2,1(θ)=0.

由引理2.2可得

同时

又由引理2.2得结果如表3所示.

表3 幂等元的值

要证明表3,只需证明第一项,其他项类似.当q≡1 (mod8)且p≡-1 (mod8)时,θs为的根当且仅当因此

gcd

这就完成了定理3.1的证明.

定理 3.2的证明对任意的首先,s任取s∈{0,1,…,n-1},则

当且仅当

又

故

gcd

同理

gcd

这就完成了定理3.2的证明.

5 实例

对文献[12]例4和例7中的二元二次剩余码[119,60],下面给出它们的幂等生成元.

首先,设

其中

A0={i|gcd(i,119)=1,1≤i≤118},

A1={i|gcd(i,119)=7,1≤i≤118}=

{7,14,21,…,112},

A2={i|gcd(i,119)=17,1≤i≤118}=

{17,34,51,68,85,102}.

其次,设

{1,2,4,8,9,11,15,16,18,22,23,25,29,30,

32,36,37,39,43,44,46,50,53,57,58,60,64,

65,67,71,72,74,78,79,81,86,88,92,93,95,

99,100,106,107,109,113,114,116},

{3,5,6,10,12,13,19,20,24,26,27,31,33,

34,38,40,41,45,47,48,52,54,55,59,61,62,

66,69,73,75,76,80,82,83,87,89,90,94,96,

97,101,103,104,108,110,111,115,117,118},

{1,2,4,8,9,13,15,16,18,19,25,26,30,

32,33,38,43,47,50,52,53,55,59,60,64,

66,67,69,72,76,81,83,86,87,89,93,94,

100,101,103,104,106,110,111,115,117,118},

{3,5,6,10,11,12,20,22,23,24,27,29,31,

36,37,39,40,41,44,45,46,48,54,57,58,61,

62,65,71,73,74,75,78,79,80,82,88,90,92,

95,96,97,99,107,108,109,113,114,116},

A1,1={7,14,28,56,63,91,105,112},

A1,-1={21,35,42,49,70,77,84,98},

A2,1={51,85,102},

A2,-1={17,34,68}.

其中

F2,1(x)=x3+x+1,

F2,-1(x)=x3+x2+1,

F1,1(x)=x8+x7+x6+x4+x2+x+1,

F1,-1(x)=x8+x5+x4+x3+1,

x31+x30+x28+x27+x26+x25+

x24+x23+x22+x21+x20+x18+

x17+x9+x8+x6+x3+x+1,

x39+x38+x337+x36+x35+x34+

x32+x30+x29+x27+x26+x24+

x22+x21+x19+x18+x16+x14+

x13+x12+x11+x10+x9+x7+

x6+x5+x4+x3+1.

表4 二次剩余码[119,60]的幂等生成元

Em

和

Em0,1,2(x)+1,