基于信息矩阵估计的极化码参数盲识别算法

刘鉴兴, 张天骐, 柏浩钧, 叶绍鹏

(1. 重庆邮电大学通信与信息工程学院, 重庆 400065;2. 重庆邮电大学信号与信息处理重庆市重点实验室, 重庆 400065)

0 引 言

极化码是2009年由Arikan根据信道极化现象提出的一种理论上可以达到香农极限的信道编码方案,该编码技术相比于Turbo码和低密度奇偶校验(low-density parity-check,LDPC)码,其优势体现在编译码复杂度低、理论可达香农极限以及在中短码下拥有更好的误块率(block error rate,BLER)性能等。由于极化码优异的性能,我国提出的极化码方案被选定为5G中eMBB(增强移动带宽)场景控制信息信道的编码方案。现在中国的IMT-2020(5G)推进组已经在实用的场景下对极化码进行了测试,测试结果满足国际电信联盟对于传输速率、低通信时延和海量终端连接等要求。极化码在卫星通信和深空探测方面也有不错的应用前景。

近几年来,信道编码参数盲识别已成为非合作信号处理领域中的研究热点问题。极化码是一种非系统线性分组码,针对线性分组码的盲识别研究比较多且较成熟。文献[4]提出秩准法,利用秩亏的现象识别线性分组码码长,但是该算法只能用于无误码的情况。文献[5]利用高斯列消元后的分析矩阵,计算出各列列重及其均值和方差,并根据均值差值和方差差值来识别码长。文献[6]将循环码的候选校验矩阵与二进制流构造的截获矩阵相乘,并根据判决门限得到的校验矩阵识别出码长、同步时刻和生成矩阵。文献[7]针对里德-所罗门(Reed Solomon,RS)码提出了一种软判决算法,遍历本原多项式进行初始码根匹配并利用平均校验符合度识别码长和本原多项式。除此之外,对于其他信道编码的盲识别研究也较成熟,比如递归型系统卷积码(recursive systematic convolutional code,RSC)、LDPC码和Turbo码。但是目前国内外针对极化码参数的盲识别研究很少,文献[14]采用遍历码长和删除概率的方法来构造零空间矩阵,通过与码字比特流迭代相乘的匹配度来识别码长和信息比特位数。该方法需要遍历两个参数,复杂度较大。文献[15]通过删除生成矩阵的一行来构造对偶向量,根据不同码长的码率特性来识别码长和信息比特位数和位置。该方法复杂度也较大,识别码长时需要正确识别每个码长下的码率,这会大大降低可靠性。

由于极化码属于非系统码,其分析矩阵不具有系统码的一般性质,且没有Turbo码码字与生成多项式之间的关系。所以传统的方法无法有效地识别极化码参数。针对极化码识别困难的问题,本文利用其生成矩阵已知且满秩这一特性,提出了一种基于信息矩阵估计的极化码参数盲识别算法。该算法首先利用生成矩阵的逆矩阵和截获比特流构造的码字矩阵得到估计的信息矩阵,在无误码情况下根据映射之后的分析矩阵所含的信息识别出码长、信息比特位数和位置分布,在有误码的情况下利用分析矩阵在零均值比下的峰值识别出码长,再根据该码长的分析矩阵识别出信息比特位数和位置分布。

1 极化码原理

1.1 信道极化理论

信道极化理论是Arikan在2008年提出的,信道极化分为信道合并和信道分裂两部分。信道合并指以递归的方式将给定的B-DMC(二进制输入离散无记忆信道)组合成矢量信道::→,这里的,分别表示输入输出符号集合,=2,≥0。递归从第0阶(=0)开始,递归的第1阶(=1)是将两个独立的信道组合成信道:→,如图1所示。

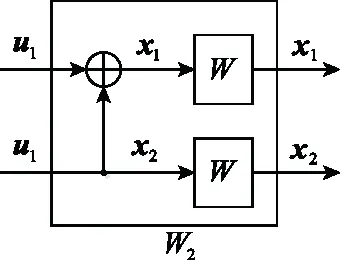
图1 信道W2Fig.1 Channel W2

根据以上的递归规律,可以依次得到信道,,…,,…的结构。信道的结构如图2所示。

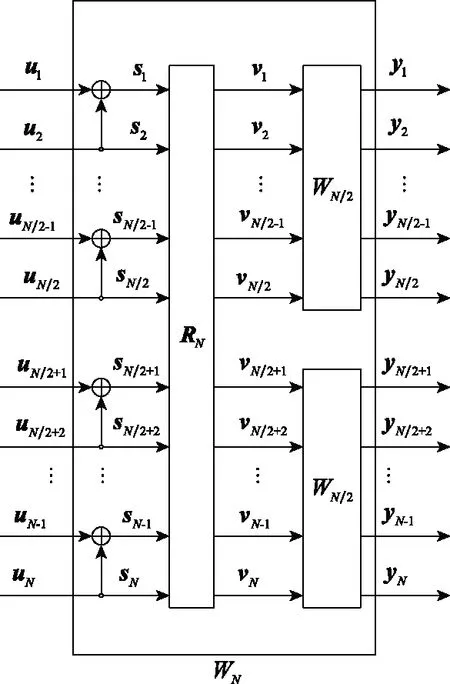
图2 信道WN的结构Fig.2 Structure of channel WN

图2中,表示比特翻转操作,目的是将输入序列进行重排,先排奇数元素,再排偶数元素。经过Arikan教授的证明,当趋近无穷的时候,子信道的容量会呈现两极分化,一种是信道容量为1的无噪声信道,另一种是信道容量为0的纯噪声信道。

信道极化是极化码的理论依据,其编码思想就是将信息比特用信道容量为1的无噪声信道传输,冻结比特用信道容量为0的噪声信道传输。

1.2 极化信道可靠性估计

信道可靠性估计是为了挑选出适合传输信息比特的信道。Arikan提出使用巴氏参数和对称信道容量来计算B-DMC的可靠性和信道的传输速率。首先介绍巴氏参数()和对称信道容量()的定义:

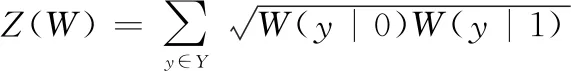
(1)

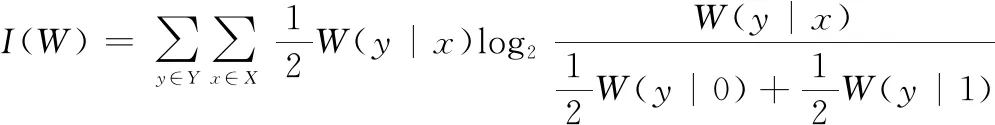
(2)

式中:(|)表示信道转移概率;()是使用信道等概率传输0、1时的最高速率;()是当传输0或1时最大似然判决错误概率的上限。当删除概率为时,就有()=,则()∈[0,1]。

对于任意B-DMC对称容量和巴氏参数之间都有如下关系:

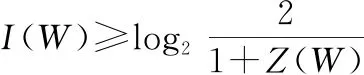
(3)

(4)

可以得到当巴氏参数()越小,对称信道容量()越大,信道就越可靠,反之则()越小,信道就越不可靠。

对于任意B-DMC子信道的巴氏参数计算递归过程如下:

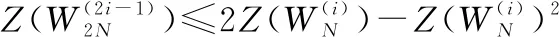
(5)

(6)

当信道为二进制删除信道(binary erasure channel, BEC)时式(5)中可以取等号。根据式(5)和式(6)可以计算出BEC各个子信道的错误概率,比较大小就能得到错误概率最小的个子信道。图3给出了BEC信道在删除概率为0.5时,各个子信道的巴氏参数分布情况。从图中可以看出经过信道极化后巴氏参数趋近于0和1,即信道的可靠性呈现为两个极端。

图3 BEC巴氏参数分布Fig.3 Bhattacharyya parameter distribution in BEC

1.3 极化码编码

极化码是一种二元线性分组码,其码字序列可以用信息序列和生成矩阵相乘得到:

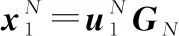
(7)

=⊗

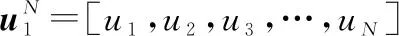
(8)

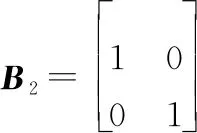
(9)

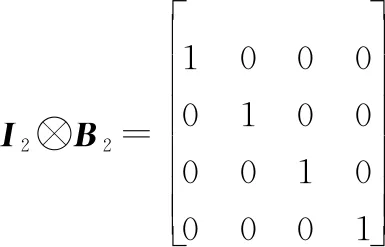
(10)

式中:表示2阶单位矩阵。矩阵由变化得到,先将中奇数列排入前2列,再将偶数列排入后2列，和分别表示为

(11)

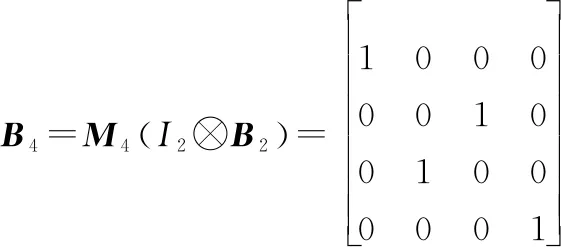
(12)

(13)

2 极化码盲识别原理

2.1 识别数学模型

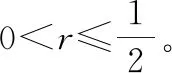
2.2 识别原理

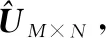
⊗⊗=,表示=2阶单位矩阵。

采用数学归纳法证明

容易证明·=

假设⊗·⊗=2

根据克罗内克积运算可以得到⊗(+1)

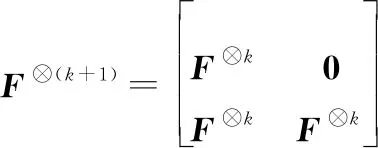
(14)

那么

(15)

则有⊗·⊗=。

证毕

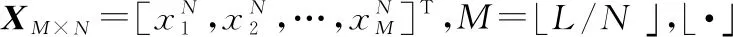
(16)

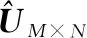
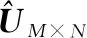
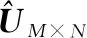
证毕

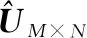
证毕

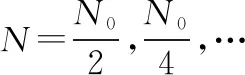
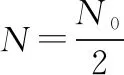
证毕

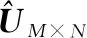
2.3 极化码参数识别方法

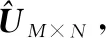
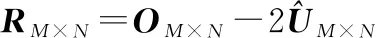
(17)

式中:×表示×阶的全1矩阵。定义()为×第列中元素1的比例减去元素-1的比例,即

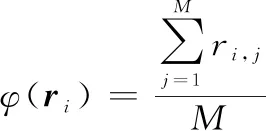
(18)

式中:(=1,2,…,)表示×中第列向量;, 表示×中第行第列元素。当不存在误码时,×中冻结比特所对应的列()=1,信息比特所对应的列()会接近于0。当误码较小的时候,冻结比特所对应的列中1的比例将远大于-1的比例,即()值会大于0。当误码较大时,冻结比特所对应的列中-1的比例会接近1的比例,即()值会接近0。这时就需要设定合适的门限值来区分对应冻结比特所在位置还是信息比特所在位置。如果在进行码长遍历的时候每个码长下都进行门限的求取和判决,不仅会大大增加复杂度而且还会降低可靠度,当遍历其中一个码长时,信息比特位数识别错误将会导致整体码率的识别错误。为了规避这个问题本文引入了零均值比的概念:

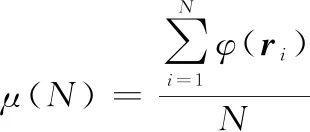
(19)

式中:()表示该码长下矩阵×中元素1的比例减去元素-1的比例,由于当遍历码长小于真实码长时,码率会大于真实码率,这会导致矩阵×中信息比特位置对应的列数增多,×中元素1的比例就会降低,则()会小于真实码长对应的()。当遍历码长大于真实码长时,码率等于真实码率,但是×会包含更多的误码,导致其中元素1的比例降低,则()也会小于真实码长对应的()。所以可以得出结论,当遍历码长等于真实码长时,()会出现峰值。因此，可以作为识别码长的依据,即

(20)

识别出码长后,再根据×中各列的()值以及门限识别出信息比特位数以及位置。

2.4 求取门限

由于在实际通信过程中,分析矩阵×会受到误码影响,通过分析×中信息比特和冻结比特对应列的(),可以得到两种不同的分布特性。再根据极大极小准则得到判决门限,×中()<对应列的索引就为信息比特位置,反之为冻结比特位置。具体过程如下。

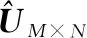
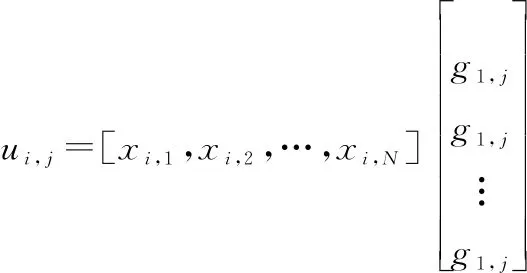
(21)

那么,×中第行第列元素, 就可以表示为

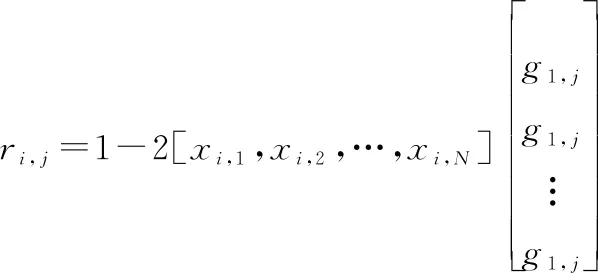
(22)

当误码率为时,对应冻结比特所在的位置。, =0要成立,需要误码的位置发生在生成多项式系数不为0的位置上，且误码个数为0或者为偶数。所以, =0的概率就为

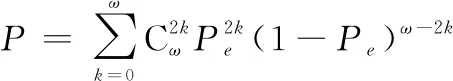
(23)

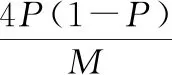
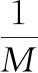
因为在非合作信道中不知道先验信息,所以采用极大极小化准则来求解门限。假设对应信息比特所在的列的事件为H,对应冻结比特所在的列的事件为H。在二元通信系统中通常采用==0,==1的代价因子。极大极小化代价的条件为

(|H)=(|H)

(24)

又因为似然函数为

(25)

(26)

设判决门限为,则有

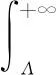
(27)

求解出极大极小化准则下的判决门限为

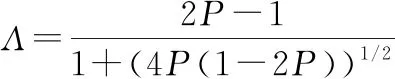
(28)

2.5 极化码参数识别步骤

根据式(19)得到该遍历码长下的()。如果=10遍历结束执行步骤6;反之,=+1执行步骤1。

比较所有遍历码长下的码率,并根据遍历码长大于等于真实码长后码率不变这一特点识别码长,输出该码长下的信息比特位数以及位置。

比较所有遍历码长下的()值,根据式(20)识别出码长,根据识别出的码长计算信息矩阵的各列门限值,统计分析矩阵中()<的数量和位置,其值就为信息比特位数,其位置就为信息比特位置。

3 仿真分析

3.1 无误码仿真验证

本节的仿真实验是以参数(32,12)、(64,32)和(128,64)的极化码为例来进行分析,接收端接收到了无误码的500组码字比特流,且通过二进制删除信道进行传输,二进制删除概率=01。各个遍历码长求出的码率和分析矩阵各列()如图4所示。

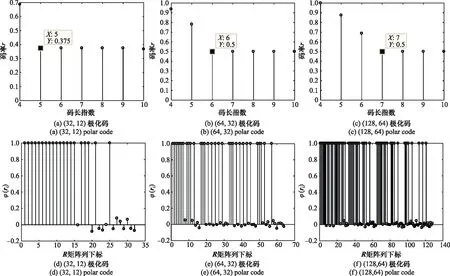
图4 无误码码长、信息比特位数以及位置识别Fig.4 Error free code length, information bits and location identification

从图4(a)可以看出当遍历码长指数<5时,码率大于0375,这与推论1是一致的,当≥5时,码率一直保持0375不变,那么真实码长=2=32,这与第22节分析的结果一致。同理可得图4(b)和图4(c)的真实码长分别为64和128。同时可以发现当真实码长较长与码长较短的极化码相比,变成同样较小码长的极化码时,其码率会越大。这就说明推论2中码率的大小也有递推关系,码率会随着码长变短而增大。图4(d)、图4(e)和图4(f )中冻结比特所对应的列()值都为1,信息比特所对应的列()值都接近于0,这与第23节分析的结果一致。无误码情况下的识别由于不需要做门限的判决,各遍历的码长下分析矩阵各列的()=1的就识别为冻结比特的位置,其余都为信息比特的位置。

3.2 误码仿真验证

误码条件下的识别仿真也选取参数为(32,12)、(64,32)和(128,64)的极化码进行分析。条件设置与第31节相同,误码率=002。各遍历码长对应分析矩阵的零均值比(),估计码长对应的()如图5所示。

从图5(a)～图5(c)可以看出,当遍历码长小于真实码长时,()会小于真实码长对应的(),当遍历码长大于真实码长时,()也会小于真实码长对应的(),这与第33节分析的结果一致。峰值对应的码长就为真实码长64和128。图5(d)、图5(e)和图5(f )分别是码长32、64和128对应的()值。图中显示各列的门限值,可见()小于门限值的个数就为信息比特位数,对应位置就为信息比特位置,这与推论1和推论2是一致的。

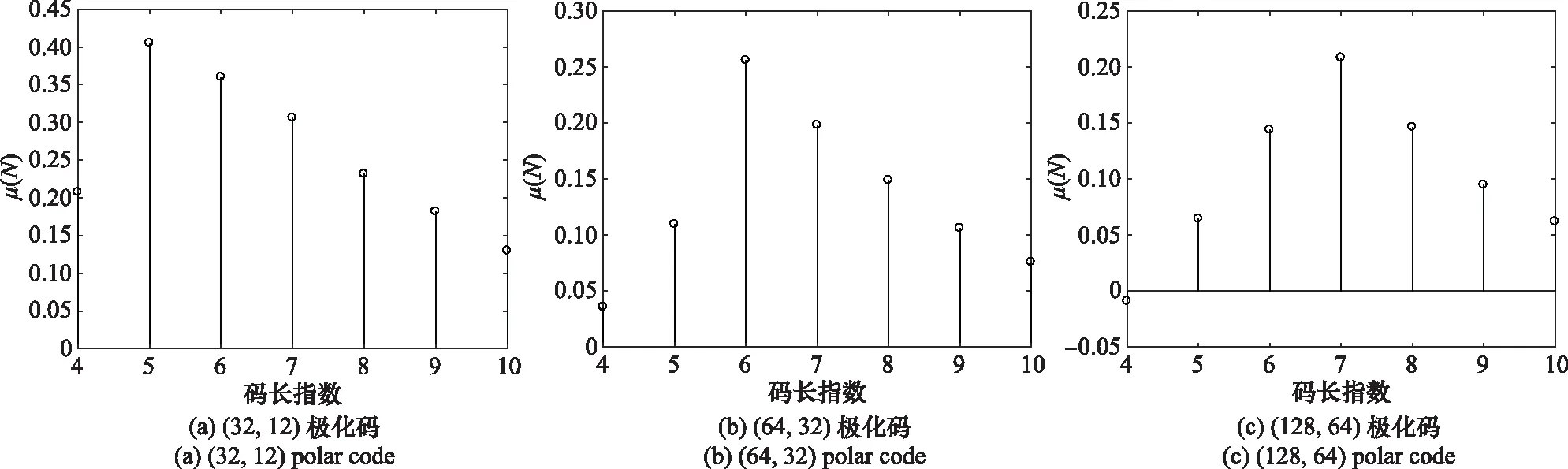
图5 有误码码长、信息比特位数以及位置识别Fig.5 Error code length, information bits and position recognition

3.3 性能分析

码字组数对识别性能的影响

本实验选取(64, 30)的极化码进行仿真分析,设定截获码字组数分别为100、300和500,采用本文算法同时对码长、信息比特位数和位置进行估计。删除概率=0.4,蒙特卡罗实验次数为500。仿真结果如图6所示。

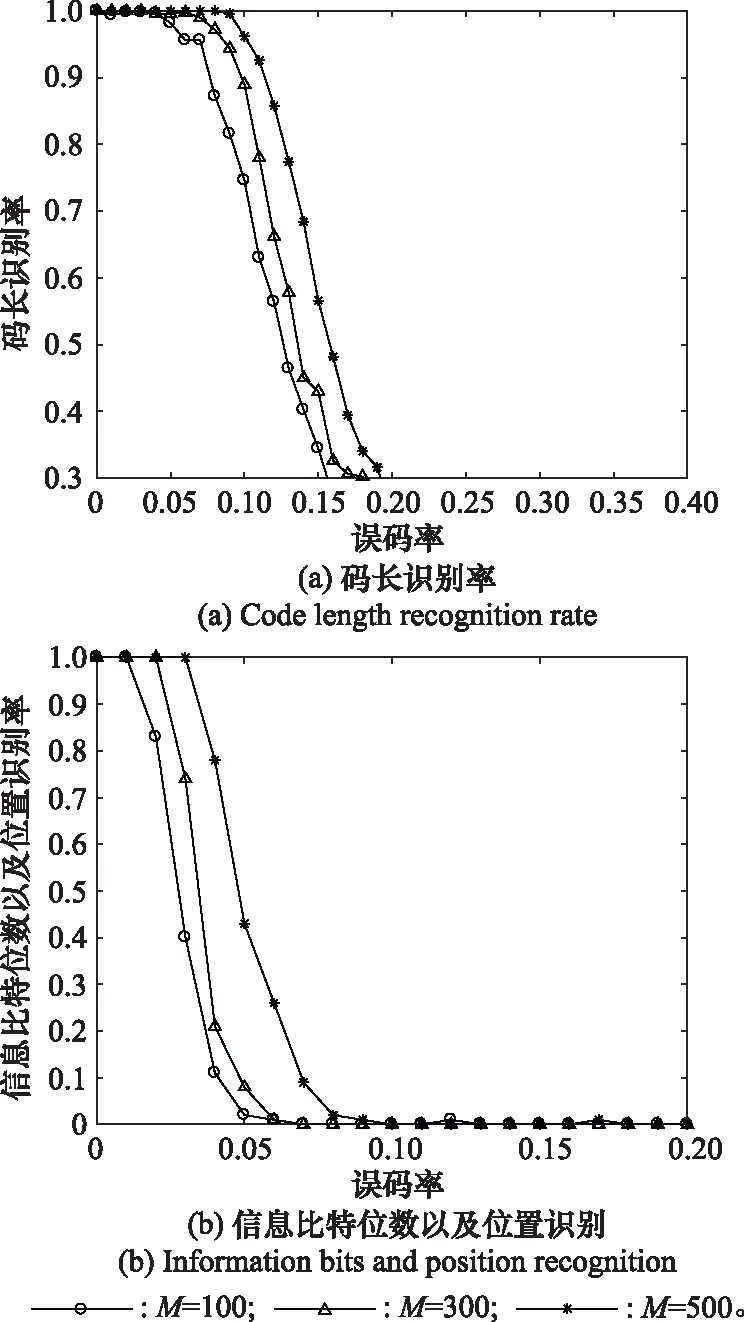
图6 不同码字组数的识别率Fig.6 Recognition rate of different code word groups

从图6可以看出码长和信息比特的正确识别率随截获码字组数增加而提高。所以可以通过增加码字组数来提高算法的容错性。并且本算法在截获码字组数为100时,仍然有较好的容错性。

码长对识别性能影响

本实验选取码长为32、64和128的极化码进行仿真分析,设定码率都为1/2,码字组数为500。采用本文算法同时对码长、信息比特位数和位置进行估计。其余参数设置与实验1相同。仿真结果如图7所示。

图7 不同码长的识别率Fig.7 Recognition rate of different code lengths

从图7结果中可以看出,码长为32时,在同误码率下,码长、信息比特位数以及位置的识别率是最高的,随着码长的增加,相关参数识别率逐渐降低。这是因为码长越长,分析矩阵中误码出现的次数也就越多,对参数的正确识别影响也就越大。但是,对于码长为128的极化码,在误码率为9×10的条件下,码长识别率依然能达到90%以上。

不同算法识别性能对比

本实验将对比分析本文算法和文献[14]算法对码长的识别性能。选取的极化码参数分别为(32,12)、(64,30)和(128,60),删除概率=0.5,截获码字组数为200,蒙特卡罗实验次数为500,对比结果如图8所示。

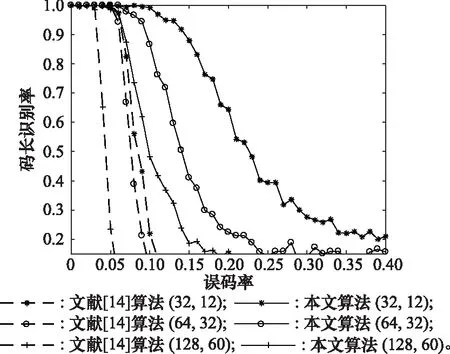
图8 不同算法的码长识别率Fig.8 Code length recognition rate of different algorithms

从图8结果来看,本文算法对码长的识别性能要远好于文献[14]算法。设定码长识别率为80%以上,对于3组极化码,文献[14]算法所允许的误码率分别为7.09×10、6.52×10、3.56×10,而本文算法所允许的误码率分别为1.65×10、1.06×10、7.54×10。由于本文算法规避了在遍历码长时对每个信息比特位置搜索这个问题,引入零均值比提高了整体码长的识别性能。所以本文算法针对码长的识别时,在误码率高的时候有更好的稳健性。

3.4 计算复杂度对比分析

文献[14]算法的计算复杂度主要集中在求零空间矩阵和计算匹配度。参数设置与本论文算法相同,该算法在不同遍历码长都会求取零空间矩阵,其计算复杂度约为(23),再与信息比特流迭代相乘并计算匹配度,其计算复杂度约为(2)。信息比特位数以及位置是通过遍历信息位数构造零空间矩阵来识别的,其复杂度约为(23),于是总的复杂度约为(23)。综上,本文算法计算复杂度更低。

4 结束语

本文利用极化码生成矩阵的逆矩阵为自身这一性质,与截获比特流构造的码字矩阵相乘得到估计的信息矩阵,在无误码情况下利用分析矩阵所含的信息推出码率随码长的分布情况,从而完成对码长和信息比特位数和位置的识别。为了提高在有误码情况下识别的可靠性,引入了零均值比计量,根据峰值识别出码长,再根据分析矩阵各列的统计特性识别出信息比特位数和位置。与其他算法相比,本文算法对码长的识别效果更好,抗噪声性能更强,复杂度更低,具有更高的工程应用价值。