MC-NOMA增强型反向散射网络中的谱能效率均衡优化

李兰花, 黄晓霞

(1. 中国科学院深圳先进技术研究院, 广东 深圳 518055; 2. 中国科学院大学深圳先进技术学院,广东 深圳 518055; 3. 中山大学电子与通信工程学院, 广东 广州 510275)

0 引 言

伴随5G、6G、人工智能、边缘计算技术的发展,移动物联网在医疗保健、智能控制、智能家居、环境监测等领域有着广泛的应用前景,但移动设备有限的续航能力成为阻碍其广泛部署的重要瓶颈。

然而,由于没有持续稳定的载波信号,大量的BD在对不稳定的环境射频信号源的强烈依赖下针对有限的传输机会展开激烈争夺。由此,同一时间呈爆发式的反向散射信号将在接入点形成强烈的干扰,从而降低网络的整体吞吐量,带来不可估计的时延。如何针对反向散射网络设计有效的多址接入方案成为了当前亟待解决的问题。

文献[28-29]中,作者分别基于正交频分多址和码分多址技术为WiFi反向散射网络设计了多址接入方案支持数十个BD的同时接入。通过提取信号状态并跟踪信号状态的转换,Canon系统和FlipTracer系统可以在恶劣信道条件下对多个反向散射信号进行并行解码。文献[32]中,Laissez-Faire系统结合时域和相位域设计多址接入方案实现多个随机(非同步)传输BD的并行接入。NetScatter系统使用分布式线性调频扩频编码在500 kHz带宽上允许256个BD并行传输。

非正交多址接入(non-orthogonal multiple access,NOMA)技术使多个信息流以不同的功率在相同的信道上传输,并行地为多个用户同时提供无线接入业务,并且可与其他域的多址接入技术相结合,大大增加了用户的接入机会。因此,一些学者针对NOMA增强型的反向散射通信网络进行了研究。文献[36]利用环境反向散射通信网络中功率的稀疏性设计NOMA方案并联合多进制调制实现并行的反向散射通信。文献[37]将不同区域或具有不同反向散射功率级别的节点相匹配后采用NOMA方案实现多路反向散射信号的并行接入。文献[38]利用无人机作为NOMA增强型反向散射网络的功率发射器和信息接收器,通过优化无人机的高度来优化网络的吞吐量。文献[39-40]结合功率域复用和时域复用设计反向散射网络的多址接入方案。文献[41-44]研究了NOMA增强型反向散射通信网络中的资源分配问题,通过时间分配、功率控制和反射系数优化来获得最佳的网络吞吐量和能效(energy efficiency, EE)。

此外,考虑到多载波系统在用户分集方面的优势,将NOMA技术应用到多载波系统中,可进一步提升网络的频谱效率(spectrum efficiency,SE)。在传统的多载波系统中,为了避免多用户干扰,将给定的射频频段划分为多个正交子载波,每个子载波最多分配给一个用户。联合功率域复用的NOMA技术后,多个用户可在同一子载波上传输,然后在接收端使用连续干扰抵消(successive interference cancellation,SIC)移除同频用户的干扰。文献[46-48]研究了多载波的NOMA(multicarrier NOMA, MC-NOMA)系统中的子载波分配和功率分配联合优化问题。

为了提高反向散射通信的可靠性,本文首先引入了具有双通信模式的BD,即主动传输(active transmission,AT)和反向散射传输(backscatter transmission,BT)。AT利用自身产生的载波信号进行信息传输可提供稳定可靠的传输,从而获得较高的传输速率。BT则将信息搭载到周围的信号上进行传输,省去了高能耗的载波产生过程,从而获得高的EE。在混合AT和BT的网络中,BT可利用AT的射频信号作为载波进行传输,可进一步提高传输的稳定性,降低因环境信号的波动带来的不可预测的时延。鉴于两种通信模式的优势互补,联合反向散射通信和主动通信可以有效地降低传输能耗，同时保证传输性能。文献[49]搭建了此类双模式电台,利用AT和BT的互补性来优化动态信道状态下的数据传输。当BT作为主要的通信模式时,AT将在BT传输失败时作为补充传输。而当AT作为主要的通信模式时,BT将用于信道状态测量。然而,本文考虑两种通信模式的相互协作,AT在传输数据的同时为BT提供载波。同时,网络中BD的模式选择将综合考虑其能量存储、信道状态以及自身传输性能要求,例如对有时延要求的高速率应用数据传输使用AT完成,而BT用于传输一些较短的多发的监测数据。

接下来,考虑如何针对具有双模式的BD构成的反向散射网络设计有效的多址接入方案。在之前的工作中,联合波束赋形和NOMA针对环境反向散射网络设计了分层多址接入方案。该方案中,波束赋形层允许多组设备的同时接入,而NOMA层则允许在各组内具有不同功率的设备的同时接入。该方案充分考虑了大量设备的同时接入,当环境射频信号出现时,尽可能多地为设备提供接入机会。但是由于环境射频信号的不确定性,网络中BD的传输机会依然没有保障。本文利用可靠性和EE优势互补的主动通信和反向散射通信进行相互协作,在尽可能提升网络EE的同时保证BD传输的稳定性。此外,为进一步提升反向散射网络的SE,本文采用MC-NOMA技术。

最后,针对MC-NOMA增强型反向散射网络建立了谱能效率均衡优化问题。该问题通过优化子载波分配、设备通信模式的选择和反射系数来获得均衡调控下的谱能效率最大化的分配方案。为求解所建立的混合整数非线性规划(mixed integer nonlinear programming,MINLP)问题,将该非凸的MINLP问题进一步分解成两个子问题,即子载波分配和反射系数优化。然后,基于Gale-Shapley匹配原理提出多对一稳定匹配算法求子载波分配并获得各BD对应的通信模式。在进行子载波匹配时,本文还给出了满足设备传输服务质量(quality of service,QoS)的最佳子载波数。最后,在给定子载波分配的情况下将原优化问题转化为凸优化问题进行求解,获得最佳的反射系数。仿真实验表明,本文提出的MC-NOMA方案能获得接近最优方案的性能,且相对于OMA的SE增长29.5%,EE增长25.9%。此外,通过调节均衡参数,该优化方案可在反向散射网络中获得所需的SE和EE。

1 系统模型

为了利用多变的环境信号,一旦有强射频信号出现,大量的BD将同时启动数据传输来抓住珍贵的传输机会。因此,在同一时间反向散射通信常常呈现爆发式的增长,进而在接收端引发激烈的信号冲突。本文采用MC-NOMA方案,联合功率域和频率域复用使大量的BD可并行地向接入点发送数据,从而大大提高BD的接入机会,降低网络时延,提高网络吞吐量。与此同时,在主动通信和反向散射通信的相互协作下,反向散射网络的EE和传输稳定性可同时获得保障。本节首先介绍了混合主被动通信的BD架构,然后利用具有双通信模式的BD构建MC-NOMA增强型反向散射网络。

1.1 混合主被动通信的BD

如图1所示,具有双通信模式的BD,即包含AT和BT。

图1 具有双通信模式的BD组成模块Fig.1 Building blocks of BD with dual-transmission mode

主要包括如下组成模块:

(1) 射频能量采集器将接收到的射频信号转换成直流电能输入能量存储器。

(2) 能量存储器用于存储采集的能量，并为设备中的其他模块供电。

(3) 主动收发器用于AT的数据接收和发送,包括调制解调、编解码等处理。

(4) 载波发生器将一定频率的振荡信号输入主动收发器，用于信号的调制和解调。

(5) 反向散射解调器是将接收的反向散射信号在包络检波后和阈值进行比较，获得比特序列，从中恢复数据。

(6) 负载调制器根据比特序列进行阻抗切换，对环境信号产生不同的反射/吸收状态，实现信号的调制。例如,在开关调制中,当负载阻抗与天线阻抗相匹配时信号处于吸收状态,而当负载阻抗与天线阻抗不匹配时信号处于反射状态。

(7) 低功耗微处理器对系统各模块的操作进行控制和优化。

1.2 MC-NOMA增强型反向散射网络

MC-NOMA增强型反向散射网络模型如图2所示。假定在该网络中存在个BD,即{BD,BD,…,BD}。总的系统带宽被划分为个正交的子载波。每个子载波可分配给多个BD。BD利用个子载波{,,…,}并行地向反向散射接入点(backscatter access point,B-AP)发送数据。由于各子载波间相互正交,从而对每个子载波的符号检测处理是独立的,且可并行进行。子载波内采用功率域的NOMA方案,在B-AP处利用SIC机制可对接收信号进行解码。SIC的具体流程包括:首先从最强的信号开始解码,将组内其他信号视作干扰信号,解码后将该信号从接收信号中剔除;接着对信号强度次之的信号进行解码并从接收信号中剔除,同样将剩余信号视作干扰信号;如此反复,依次解码组内的所有信号。注意,结合文献[52-53]中的异步NOMA信号检测方法,各BD间可采用异步传输方式,无需进行复杂的同步操作。

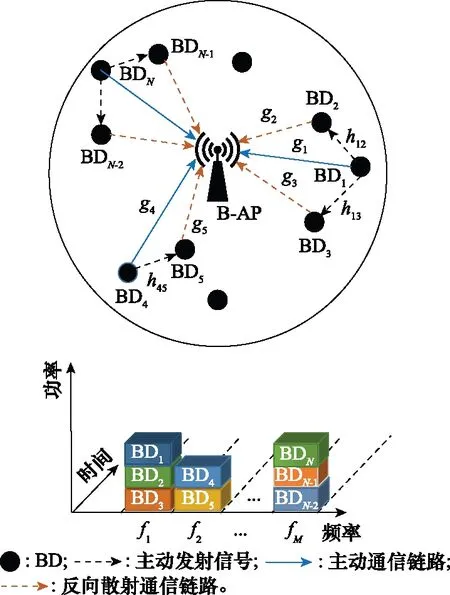
图2 MC-NOMA增强型反向散射网络模型Fig.2 Model of MC-NOMA enhanced backscatter network

为避免高速率的主动通信设备之间的干扰,每个子载波内只有一个设备进行AT传输,同一子载波内的其他设备则利用AT信号作为载波进行BT传输。如图2所示,设备BD,BD,BD同时占用子载波,BD采用AT传输,BD和BD则利用其发射的信号进行BT传输。BD和BD之间的信道增益表示为,而BD到B-AP的信道增益表示为。若BD利用BD的AT信号作为载波进行BT传输,则受到双向的信道衰落影响,等效的反向散射信道增益为=。

2 谱能效率均衡优化

与反向散射通信相比,主动通信不受双向信道衰落影响,可提供更高的传输速率。反向散射通信则将数据搭载在AT信号上传输,获得更高的EE。由于子载波内采用NOMA方案,子载波的分配将决定同组BD之间的干扰强度，进而影响SE。因此,网络的谱能效率和BD传输模式的选择以及子载波的分配密切相关。此外,在NOMA方案中,接收信号的功率决定了SIC的效率以及BD的传输速率。通过调节反射系数可改变反向散射信号强度，进而改变反向散射信号到达B-AP的接收功率。因此,通过调节BD的反射系数来改变接收信号的功率,可进一步优化网络性能。

本节首先针对MC-NOMA增强型反向散射网络提出了谱能效率均衡优化问题。然而,该优化问题是MINLP问题,也是非凸的。为了降低问题的复杂度,本文将谱能效率均衡优化问题进一步分解成两个子问题,即子载波的分配和反射系数的优化。然后,利用多对一稳定匹配算法求最优的子载波分配和BD对应的传输模式。最后,在给定子载波分配的情况下,求出满足条件的反射系数。

2.1 优化问题描述

=

(1)

令上所有BD按反向散射信道增益的降序排列,即若>则有<。用SIC接收器对上的信号做解码处理后,各BD对应的接收信号只受到强度比其低的信号的干扰,则上BD设备的信噪比为

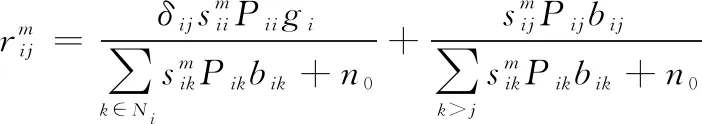
(2)

式中:等式右边的第1项是AT设备的信噪比,第2项是BT设备的信噪比;是BD的邻接节点集合;表示高斯白噪声功率;是克罗内克函数用于标识下标是否等于,即

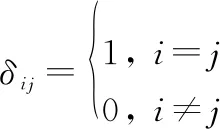
(3)

最后,子载波上的吞吐量可表示为

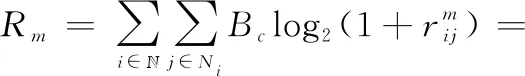
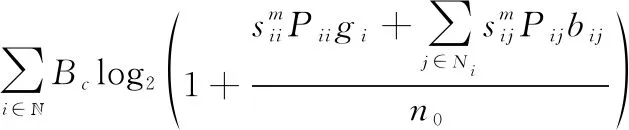
(4)

反向散射网络总的吞吐量表示为

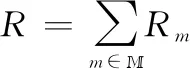
(5)

每个子载波的带宽为,而所占用的子载波数等于采用AT传输的BD数,因此数据传输所占用的总的信道带宽可表示为

(6)

反向散射网络的SE定义为单位带宽传输频道上可传输的数据量,根据式(4)～式(6)可知,反向散射网络的SE为

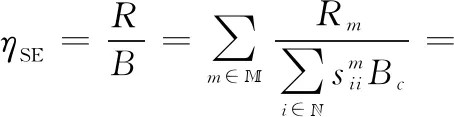
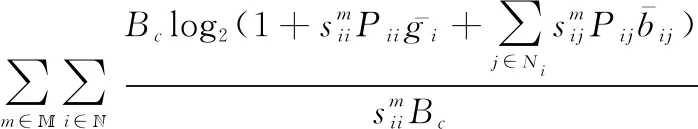
(7)

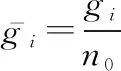
令和分别表示AT的电路功耗和BT总的功耗,数据传输总的功耗包括AT传输节点的传输功耗、电路功耗以及BT传输节点的总功耗,即

(8)

最后,反向散射网络的EE定义为消耗单位能耗所能传输的数据量,根据式(4)、式(5)和式(8)可知反向散射网络的EE为

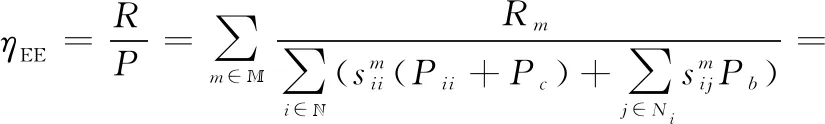
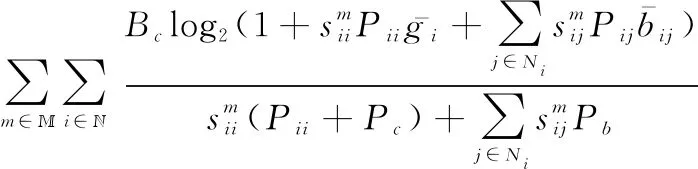
(9)

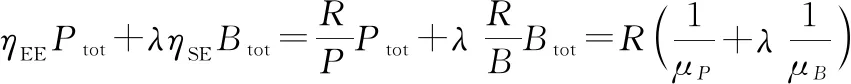
(10)

式中:为均衡参数，用于控制SE和EE的权重;=和=则分别表示带宽占用率和功率使用率。

令∈×和∈×1分别表示通信模式矩阵和发射功率矩阵。则谱能均衡优化问题可表示为

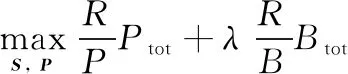
(11a)

s.t.

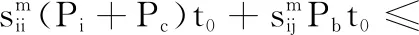
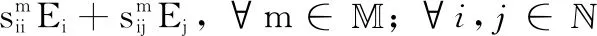
(11b)

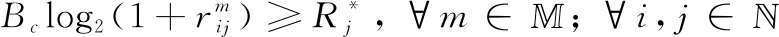
(11c)

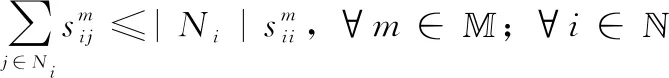
(11d)

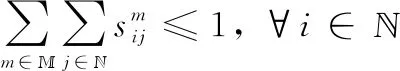
(11e)

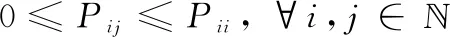
(11f)

(11g)

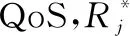
优化问题式(11)是MINLP问题,通常需要用全局搜索法来获得最优解,具有指数复杂度。然而,指数复杂度的算法对于大规模低功耗的反向散射网络而言并不适用。因此,将该问题拆分成两个子问题,即子载波分配和反射系数的优化,然后分两步利用低复杂度的算法进行求解。第1步,利用多对一稳定匹配算法将BD分配到不同的子载波,并确定BD的通信模式。第2步,根据给定的子载波分配,优化每个子载波上BD的反射系数，从而达到最大的谱能效率。

2.2 多对一稳定匹配算法

鉴于各子载波内限定唯一的主动通信设备,同时每个BD只处于某一个子载波上,子载波分配可视作一个主动通信设备和多个BD的匹配过程。因此,采用多对一稳定匹配算法来确定子载波的分配。

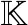
(12)

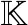
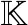
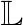
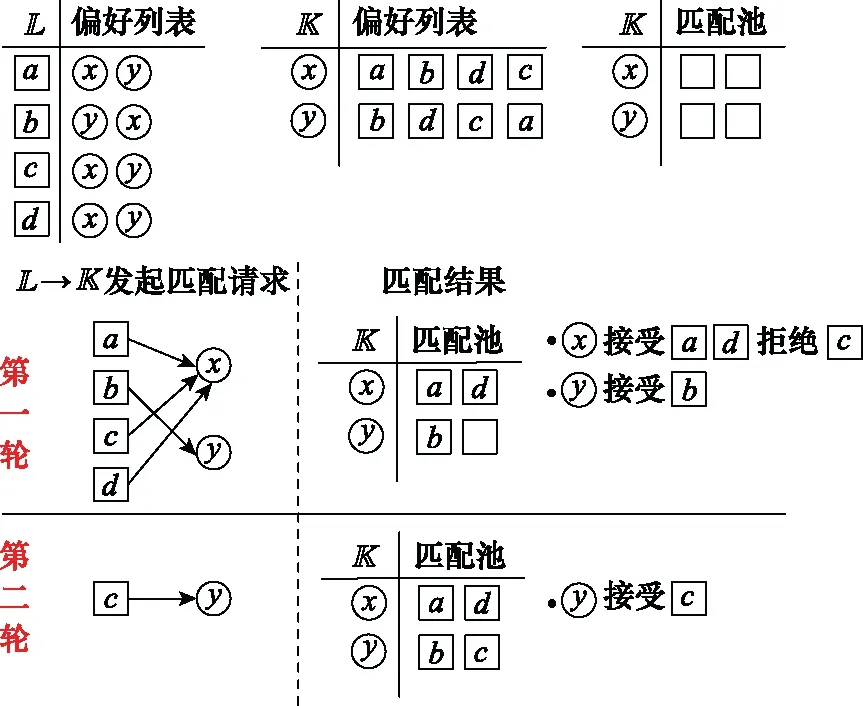
图3 多对一稳定匹配示例Fig.3 Example of the many-to-one stable matching

接下来,考虑如何确定值,即子载波的占用数和主动通信设备数,该值将直接影响网络的SE和EE。

为满足QoS各子载波上的BD需满足的最小速率要求,将式(2)代入式(11c)，可知BD在上做AT传输时可承受的最大干扰为

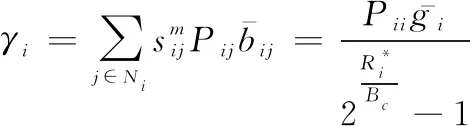
(13)

由式(12)和式(13)网络的总吞吐量可表示为

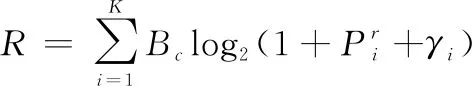
(14)

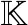
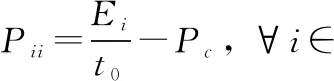
(15)

其余设备采用BT,则总的功耗为

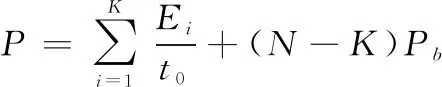
(16)

此外,子载波的占用数等于AT的设备数,所以总的占用带宽=。

最后,根据谱能效率优化目标式(10),值由式(17)确定,即

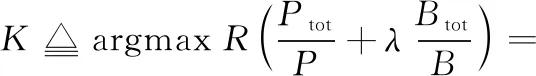
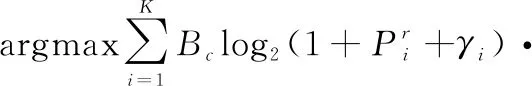
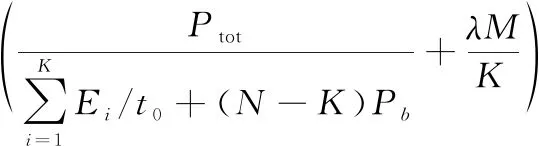
(17)

算法1给出了基于多对一稳定匹配算法的子载波分配,针对子载波占用数不确定情况下的子载波进行分配,并确定BD的传输模式。

算法 1 基于多对一稳定匹配算法的子载波分配输入 BD集,子载波集 ,储能Ei,传输时长t0,信道增益gi、hij输出 传输模式矩阵S(1) 初始化 =Ø, =Ø,K=0,S=0,匹配池Λ={(i;Ø), ∀i∈ }确定子载波占用数K值:(2) 根据式(12)对设备进行降序排列(3) for k=1:M(4) 根据式(17)计算RPtotP+λBtotB ,输出取最大值时的K值(5) end for多对一稳定匹配过程:(6) 令 ={1,2,…,K}, ={K+1,K+2,…,N}(7) 根据信道增益|hij|的降序排列确定各BD的偏好列表(8) 循环(9) 集合 中未进入匹配池的BDj(∀j∈ ,j∉Λ),根据偏好列表向当前排在第一位的设备BDi(i∈ )发起“匹配请求”(10) if BDj位于BDi在偏好列表中当前所有请求设备的前qm位(11) BDi向BDj回复“接受”(12) 更新匹配池Λ(13) elseBDi向BDj回复“拒绝”(14) end if(15) until所有设备完成匹配(16) 根据Λ={(i;j), ∀i∈ ,j∈ }中的匹配结果为S赋值siii=1,siij=1

算法1主要包含两个部分,即子载波占用数值的确定和多对一稳定匹配过程。值的确定过程首先是对个BD进行排序,然后对式(17)经过次简单运算即可获得最佳的值。由于对个BD进行排序的时间复杂度为(log),确定子载波占用数值的复杂度为(log+)。其次,稳定匹配过程中将个AT设备和-个BT设备进行匹配,最多经过((-))轮即可达到稳定匹配。最终,算法1的时间复杂度为(log+-+)。

2.3 反射系数优化

给定子载波的分配和BD的通信模式,带宽占用率和功率使用率的值确定,根据式(10)谱能均衡优化目标可转化成最大化吞吐量。此外,由第22节可知,采用AT传输的BD为提高总的吞吐量将尽可能地提高传输功率,则AT设备的传输功率由式(15)给出。最后,优化问题式(11)转化为反射系数优化问题:

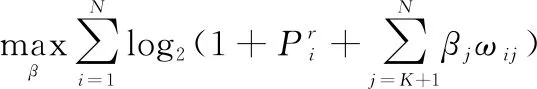
(18a)

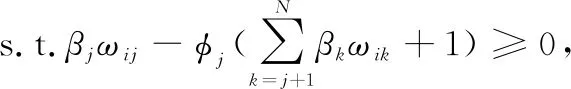
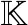
(18b)

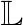
(18c)

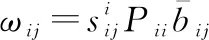
引入拉格朗日乘子{ϑ}、{}、{},式(18)的拉格朗日函数可定义为

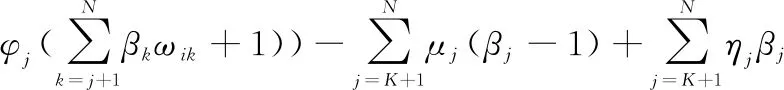
(19)

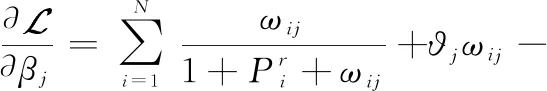
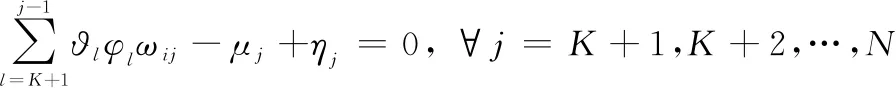
(20)

互补松弛条件包括:

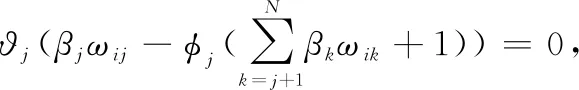
∀=+1,+2,…,

(21)

(-1)=0, ∀=+1,+2,…,

(22)

=0, ∀=+1,+2,…,

(23)

以及对偶可行性约束条件为

ϑ≥0,≥0,≥0, ∀=+1,+2,…,

(24)

最后,由原始可行性约束条件式(18b)～式(18c)和式(20)～式(24)共同构成了KKT条件,采用经典的内点法即可获得反射系数优化问题式(18)的最优解。

由于反射系数的个数为-,则使用内点法求解凸优化的反射系数优化问题式(18)的时间复杂度为((-))。综合第22节中使用算法1求子载波分配的复杂度,本文所提出的分阶段优化算法的复杂度为((-)+log+-+)。然而针对谱能效率优化问题式(11),传统的求解该MINLP问题的分支定界算法其复杂度为(2)。因此,本文所提多项式时间复杂度的算法更适合于大规模反向散射通信网络的资源分配。与此同时,由于整体的资源配置优化在B-AP处完成,并不会给极低功耗的BD带来额外的负担。此外,仿真实验表明本文所提算法可获得与分支定界算法接近的谱能效率。

3 性能仿真分析

本节对所提出的优化方案进行仿真并分析其性能。假定BD随机均匀地分布在100 m×100 m的范围内,在单位时长内进行传输,即=1。各BD的初始能量服从均值为100 mW,方差为50的正态随机分布。将AT传输需满足的最小速率设为100 kbps,而BT传输需满足的最小速率设为10 kbps。表1给出了实验仿真中使用的一些基本参数设置。

表1 实验仿真参数

通过将本文提出的MC-NOMA方案和最优方案(Optimal)、文献[58]提出的D-NOMA方案以及OMA方案进行对比来评价所提算法在SE和EE方面的性能。这里,Optimal采用全局搜索的方式给出最佳的分组和反射系数分配方案。D-NOMA是根据信道增益大小和正交性对设备进行分组后进行功率分配优化。OMA将BD按照接收信号强度降序排列,然后将排在前的BD分配到个子载波上采用主动通信模式。由此可知,OMA中各传输设备之间不存在干扰。但当子载波数小于设备数时,OMA中信道被完全占用,剩余的-个设备将无法向B-AP发送数据。

给定设备数和子载波数为20,图4给出了不同均衡参数对谱能效率的影响。

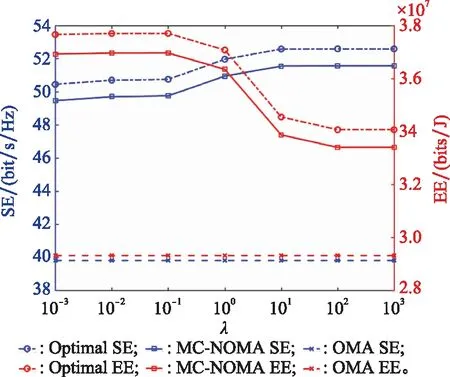
图4 不同均衡参数λ对谱能效率的影响Fig.4 Impact of the tradeoff coefficient λ on SE

Optimal和MC-NOMA的SE随λ的增大而增长,同时EE随的增大而降低。当取较大值或较小值时,SE和EE均趋于稳定。具体来说,当大于10时,Optimal和MC-NOMA着重优化SE,而当小于0.1时,Optimal和MC-NOMA着重优化EE。当=1时,SE和EE均接近最大值,其中SE相对于最大值(=∞)仅下降了1.2%,而EE相对于最大值(=0)仅下降了1.5%。由谱能效率均衡优化目标式(10)可知,当=∞时,优化方案变为最大化SE。然而,当=0时,优化方案变成最大化EE。而图4中,较大和较小时的谱能效率变化都不大,表明当较小时仍能获得与最大化SE接近的性能,而当较大时也仍能获得与最大化EE接近的性能。这都得益于本文提出的归一化的谱能效率均衡优化目标。通过总功率预算和总的可使用带宽对优化目标进行归一化后,优化方案在受到均衡参数的调节的同时侧重于网络整体的吞吐量性能。由此可见,本文通过和对谱能效率优化目标式(10)进行了有效的归一化处理,从而在不同均衡参数下均能获得较高的谱能效率。在OMA中,子载波的分配是恒定的,使得带宽占用率也是确定的,因此OMA中SE和EE不随的变化而变化。

Optimal中联合分支定界算法和内点法对节点进行分组和反射系数优化,其计算复杂度为(2)。OMA方案中根据节点接收信号强度对节点进行排序操作，进而分配到不同的子载波,其计算复杂度为(log)。此外,由第2.3节可知,本文所提出的MC-NOMA方案的计算复杂度为((-)+log+-+)。如图4所示,Optimal利用指数时间复杂度算法来换取最佳的性能。MC-NOMA具有多项式时间复杂度获得的SE和EE分别是Optimal的98%和97.8%。这也说明了本文提出的优化算法在降低了计算复杂度的同时可获得与Optimal方案接近的性能。此外,MC-NOMA的SE和EE相对于OMA分别增长了29.5%和25.9%。MC-NOMA能带来更高的SE得益于NOMA方案支持同载波内多设备的同时传输,另外在相同子载波内其他设备均可以利用主动通信设备发送的信号做低功耗的BT，从而获得更高的EE。

图5和图6分别给出了不同子载波数下的EE和SE随BD数变化的情况。

图5 EE随BD数变化的情况(λ=1)Fig.5 Number of BD versus EE(λ=1)

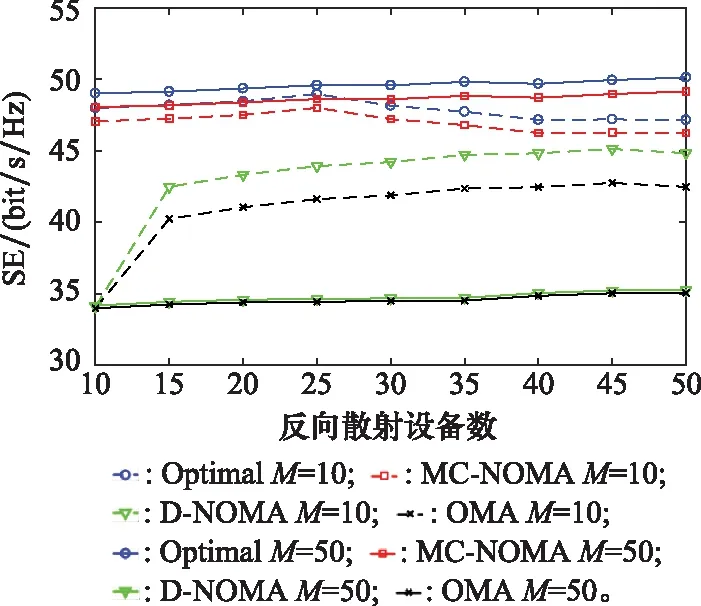
图6 SE随BD数变化的情况(λ=1)Fig.6 Number of BD versus SE(λ=1)

首先,当=10时,Optimal和MC-NOMA的EE和SE随着设备数的增加先增后减。这是因为在给定的载波带宽内增加传输的设备数可提升总的吞吐量，从而提高EE和SE。但是,当设备数进一步增加到超过子载波数的2.5倍后,同组设备之间的干扰增大，从而抑制了吞吐量的进一步增加,进而导致EE和SE的降低。具体而言,当设备数为25(是子载波数的2.5倍)时,MC-NOMA获得最大的EE,相对于D-NOMA和OMA分别增加了29.4%和35.9%。当设备数增加到40(是子载波数的4倍)时,MC-NOMA的EE在3.26×10bit/J处趋于平稳。不同于D-NOMA仅根据信道状态条件对设备进行分组,MC-NOMA在对BD进行分组时,根据满足设备能量约束和QoS需求下的最大化谱能效率优化目标确立了具体的子载波的占用数,随后利用多对一稳定匹配算法确定了各子载波上的BD。因此,MC-NOMA提供了更高的谱能效率。此外,得益于子载波上多个低功耗BD使用NOMA方式同时接入,D-NOMA在=10且设备数大于10时也获得了相对于OMA更高的EE和SE。相应地,由图6可知,SE同样在设备数为25时达到最大,此时MC-NOMA的SE相对于D-NOMA和OMA分别增加了12%和41%。而当设备数到40即子载波数的4倍时,MC-NOMA的SE在46.2 bit/s/Hz处趋于稳定。

当=50时,Optimal和MC-NOMA的EE和SE均随着设备数的增加而增加。此时设备数没有超过载波的承载量,随着设备数的增加,总的吞吐量增加,从而提升整个网络的EE和SE。但是,在OMA方案中,在子载波数为50时获得的EE和SE反而低于子载波数为10时。这是因为当子载波数增加,OMA中的载波占用率随之增加,低速率的设备同样独占子载波,导致SE降低。同时低速率的设备中的电路损耗进一步降低了网络整体的EE。此外,当子载波数超过设备数时,D-NOMA中各BD单独占用一个子载波,与OMA方案一致。因此,当=50时,D-NOMA的性能与OMA方案相同。

最后,为了分析信道增益差对系统性能的影响,给出了不同方差瑞利衰落环境下的SE和EE性能。给定子载波数为20及设备数为50,图7和图8中分别给出了不同方差对EE和SE的影响。各方案的EE和SE均随着的增大而增长。这是因为的增大促使信道功率增益的增加,并进一步提高了信号的接收功率。此外,NOMA方案(即MC-NOMA和D-NOMA)的谱能效率增长速度明显高于OMA方案。这得益于的增大提高了信道增益的差异性,从而降低了SIC操作过程中的同频干扰,并进一步提升了NOMA方案的谱能效率。

图7 EE随方差σ2变化的情况(N=50,M=20)Fig.7 EE versus σ2(N=50,M=20)

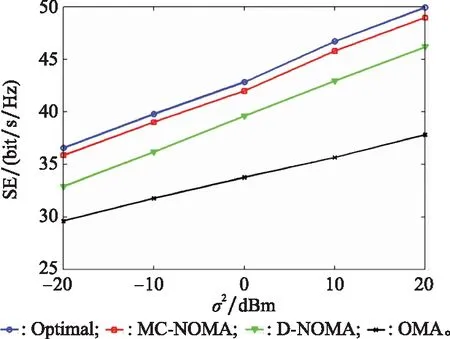
图8 SE随方差σ2变化的情况(N=50,M=20)Fig.8 SE versus σ2(N=50,M=20)

由图7所示,Optimal和MC-NOMA的EE明显高于D-NOMA和OMA。同时,当σ低于-10 dBm时,MC-NOMA方案的EE保持相对平稳。这表明MC-NOMA方案在较低σ的情况下,有效的子载波分配和反射系数优化仍能提供稳定的反向散射通信,从而提升网络的整体EE。这是由于稳定匹配算法中,主动发起请求匹配的一方总是获得优势,即请求方在保证匹配稳定的情况下总能获得当前的最佳匹配。因此,在子载波分配过程中,本文提出的多对一稳定匹配算法内处于请求方的低功耗BT设备将更具优势。此外,本文利用主被动通信的相互协作提升反向散射通信的可靠性同时降低网络能耗,从而相对于D-NOMA和OMA获得了更高的EE和SE。

4 结束语

本文首先介绍了具有双通信模式的BD,即AT和BT。通过主动通信和反向散射通信的相互协作来提升网络的EE同时保证传输的稳定性。接着,利用MC-NOMA技术提高BD的接入机会,降低网络时延,提升网络吞吐量。针对MC-NOMA增强型的反向散射网络,本文综合研究了BD通信模式的选择,子载波分配和反射系数优化,旨在提升网络整体的谱能效率。仿真实验表明,本文提出的多对一稳定匹配算法在有效地降低原优化问题的求解复杂度的同时获得了接近Optimal算法的谱能效率。相对于D-NOMA和OMA,MC-NOMA的谱能效率均有了显著提升。此外,仿真部分还分析了均衡参数对SE和EE的影响,通过调节该参数可获得所需的谱能效率性能。