基于最大期望算法的多时变信号DOA估计方法

范保华, 左 乐,*, 唐 勇,2, 胡泽华

(1. 中国电子科技集团公司第二十九研究所, 四川 成都 610036; 2. 电子科技大学电子科学与工程学院, 四川 成都 611731)

0 引 言

辐射源参数估计问题在雷达、声呐、麦克风阵列、射电天文以及移动通信中有广泛应用,因此其在阵列信号处理领域具有重要的研究价值[1-5]。微波测向通过在不同空间位置布置天线接收来波的电磁信号进行。根据布置天线的方式可分为静态阵列和时变合成阵列。静态阵列每个单元均配有对应的接收通道,通过不同阵元同时采集空间中来波信号的场分布,并通过参数估计等方法完成测向[5]。静态阵的优点是可以完成单脉冲测向,但缺点在于需通过较多的天线和相应的接收通道来解模糊及高精度测向。

与同时采集来波信号场分布的静态阵不同,时变阵列在测量过程中移动采样位置,通过时间积累和空间扫描,利用简化的采样硬件获取来波的空间场分布信息。将同时采集用分时采集替代,在处理时间与硬件资源之间进行权衡。

无源合成阵列(passive synthetic array, PSA)既是典型的时变测向阵列。其通过较少的采样单元数目,通过分时改变阵元位置来实现一维或二维场分布采集[6-7]。1996年,Friedlander首次将时变阵列用于测向,将静态阵基于本征值的测向方法应用于时变阵[6]。

无源合成阵列由于其简单的系统架构和较高的测向精度被广泛应用,但在实际工程应用中易遇到以下难点:

(1) 信号分选问题。采用静态阵测向时,由于采用多通道同时采样,可同时测量每个信号的幅度、频率、相位等信息,并以此计算得到该信号的入射角。然而采用时变阵测向时,每一次采样仅能获得入射场的幅度、相位、频率等数据,无法建立多个数据间的显性关联。当多个辐射源在同一时间段内交替辐射信号时,采样数据相互交错,但又无法事先获得单个采样数据与其辐射源的对应关系。反观入射角的估计,需首先完成信号分选,建立每个采样信号与辐射源之间的关联关系,才能采用来自同一个辐射源的数据进行该辐射源信号参数的精确估计。

(2) 采样过程中信号幅度时变问题。如对于来波为波束扫描的雷达信号[7],在不同时刻收到信号幅度不同,导致其接收的信噪比不稳定,而不同信噪比(signal to noise ratio, SNR)的信号置信度不完全一样,对于高精度测向需该考虑不同质量信号对测向结果的贡献程度。

(3) 辐射信号频率时变问题。对于频率间隔大于信号带宽的信号,可以从频域上将其分为多个辐射源。但对于频率间隔小于信号带宽的信号,如跳频信号或频率调制信号,此时信号的频率时变特性就必须谨慎处理,因为若将同一辐射源产生的变频信号分为多个辐射源进行处理,则会造成信号分选错误。不仅如此,每组信号数据量的减少还会导致测向精度的下降。

(4) 信号的采样位置取决于信号到达的时间,其分布并非均匀,空间采样位置无周期性。

在众多的波达方向(direction of arrival, DOA)估计方法中,最大似然(maximum likelihood, ML)方法被认为性能稳健且统计效率较高[5,8-9]。同时,ML方法容易结合最大期望(expectation maximization, EM)算法[10],进行信号的分选以及多信号的参数估计。EM算法可将多信号进行分离,其最大优势在于能将多目标的优化问题分解为几个独立的单目标优化问题,通过反复迭代将问题降维,从而实现运算量的缩减。Weinstein和Feder首先将EM算法应用于测向领域,实现多径时延和多辐射源定位[11]。随后,Chung和Frenkel分别将EM算法应用于多目标点频信号位置信息的获取[12-13]。对于宽带信号,Mada和Lu分别将EM算法应用于信号位置参数和波形的联合估计[14-15]。

在时变测向阵列的移动形式方面,文献[16-19]将无源合成线阵用于辐射源的测向和定位。虽然无源合成线阵通过阵列的直线移动形成一个大的测向物理尺寸对空间来波进行分时采集,但其存在移动路径的左右无法分辨、移动姿态不易控制等问题。另一方面,由于阵列的旋转容易控制,无源合成圆阵可通过两传感器的旋转获取各角度下的辐射源场分布信息,用于解算辐射源的二维入射角[20-32],并实现360°的全方位角覆盖。文献[21]提出采用两天线旋转形成一个无源合成圆阵,用于地球同步轨道卫星测向。但该方法未考虑多辐射源以及相位模糊问题,因此仅适用于单辐射源以及窄带、小角度的测向系统。文献[22]基于信号子空间测向方法,但要求频率和采样间隔固定。文献[23]采用粒子群优化算法,进行目标参数计算,但是由于粒子群算法采用随机搜索策略,其全局寻优能力并不十分可靠[24]。文献[25]所采用的阵元数较大,且只适用于单信号。文献[26-27]采用多假设伪线性迭代最小二乘方法,但未考虑信号分选问题,故仅能处理单辐射源情形。对于多信号问题,文献[28]仅利用相位差信息,提出采用正交谱配对追踪方法解决了多目标问题。但由于其谱值的计算过程要求频率固定、采样位置均匀,因此仍无法适应数据采集过程中信号频率、幅度、位置间隔改变等问题。除此之外,文献[29-31]虽然实现了多目标二维角度的无模糊估计,但均未考虑各采样点信噪比各异的情况,会造成测向精度下降。

为同时解决上述4个无源合成阵列测向及分选所面临的问题,本文提出采用EM算法,同时解决频变多辐射源的测向以及信号分选问题。据笔者所知,尚未见将EM算法应用于无源合成阵列多目标测向的报道。对于每个辐射源的DOA估计,本文采用ML方法进行二维测向,并考虑每个接收信号采样位置间隔、频率、SNR均不同的情形。但直接采用复数形式的接收信号对来波方位角及仰角的ML估计是一个非线性、多维的极值问题,需要全局多维搜索,其计算量较大。由于不同DOA产生的信号相位不同,相位干涉仪同样适用于时变测向阵列。注意到接收信号的相位差与二维入射角的投影呈线性关系,本文采用相位数据推导了不同SNR条件下二维入射角的闭合形式解析表达式。其次,无源合成阵列与静态阵列相同,当涉及到采用干涉仪体制测量辐射源DOA时,会出现相位翻转的模糊问题。为了解相位模糊的多值问题,通常需要增加传感器数量来排除多值,这无疑会增加系统和算法的复杂度。通常的相位解模糊方法根据先计算出的一个粗角度来还原相位的真实值[32]。但已报道的相位解模糊方法只适合静态线阵[32-34],不能直接用于无源合成圆阵。为了解决相位模糊问题,本文先采用无模糊的复数形式的ML方法,进行粗测向,以减小谱峰搜索的运算量,再采用解模糊后的相位数据进行入射角的解析运算。最后,数值实验结果表明,本文提出的基于EM算法的能完成高精度测向,其测向误差接近克拉米劳下限(Cramer Rao lower bound, CRLB),且测向与信号分选同时完成。

1 EM算法与模型建立

1.1 EM算法

EM算法最早于1977年由Dempster等人提出[10],其思路是将用于参数估计的数据进行分组,然后在每组内进行参数的分别估计,再根据新的估计参数重新进行数据的分组,以提高参数估计的质量,并以此交替迭代,进行数据的分解与参数的估计。EM算法的流程如图1所示。随着参数似然值的增加,分组结果最终也将收敛。EM算法的的一个显著特点在于多个参数的估计不通过单次处理,而是每次参数估计后,用新参数重新划分数据,再对划分后的数据分别进行新一轮的参数估计。EM算法采用迭代的方式将一个高维问题分解成多个低维问题,通过降维实现运算量的精简。

结合多目标测向与信号问题,由于辐射源的位置在旋转周期内相对固定,因此可依据辐射源的入射角参数进行观察数据的分解,即将来自于同一辐射源的接收数据分解入一组。而接收数据与辐射源位置的关系可通过ML方法求解的二维角度参数进行表征。基于此,首先建立接收信号的模型。

1.2 接收信号模型

设间隔为d的两天线在与XOY面内旋转,旋转中心为坐标原点O,如图2所示。在一个采样周期内,该合成圆阵接收到来自P个位置固定的辐射源发出的N个信号。辐射源辐射的电磁信号频率、幅度均不相同。

由于采样时间极短,采样周期内的旋转角度可忽略不计。第p个辐射源的第n个脉冲信号的接收信号时域表达式为

Vn(t)=Anexp(jωnt+jφp(n))+en(t),n=1,2，…,N

(1)

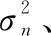
φp(n)=kp(n)dsinθpcos(φ(tn)-φp)

(2)

式中：旋转角度φ(tn)∈[0,2π)为旋转臂与x轴的夹角;仰角φp∈[0,2π)为来波方向与x轴夹角;方位角θp∈[0,π)为来波方向与z轴夹角;kp(n)=ωn/c为波数,c为波的传播速度。本文假设信号频率测量无误差。

此时,通过采样点数为M的付氏变换,将时域信号转化为频域信号:

(3)

可得第无模糊相位测量值为

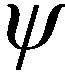
(4)

式中:ε(n)表示相位测量噪声。由于不同采样点间噪声相互独立,等效相位噪声的方差[35]为

(5)

此即为频域相位噪声与时域高斯白噪声的关系。其揭示了相位噪声与信噪比的关系,即在采样数一定的条件下,相位噪声的方差与信噪比成反比。同时,等效相位噪声服从高斯分布[36]。

当天线间距d大于半个工作波长时,会出现相位模糊问题。由于相位的测量值在[-π,π)之内,为相位的真实值对2π取模后的余数,故为

(6)

式中:h(n)为一整数,也被称为模糊数。由此可见,相位的测量值为信号的空间相差叠加相位噪声后,对2π取模后的余数。

当P个辐射源在一个采样时间内交替辐射信号,该合成圆阵的采样信号相位为P个辐射源所产生的信号相位叠加,即

(7)

2 二维入射角估计

2.1 基于相位的二维测向方法

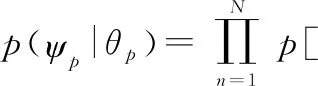
(8)

对条件概率密度函数的对数值取偏微分,并令其为零,即

(9)

和

(10)

有

(11)

及

(12)

根据三角函数的和差化积关系,以及每个相位差采样相位误差方差与SNR的反比关系,可得二维入射角的简洁表达式为

(13)

(14)

式中:b1和b2为矩阵b=[b1,b2]T的两个元素,可通过下式计算得到:

b=(det(A))-1[A][c1,c2]T,

(15)

式中:det(A)为矩阵A的行列式值。矩阵A=[(a11,a12)T·(a21,a22)T]的元素为

(16)

以及

(17)

式(16)和式(17)即通过无模糊相位值计算来波二维入射角的解析表达式。为得到无模糊相位值,还需进行模糊解算。

2.2 基于复数响应的相位模糊解算

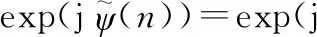
(18)

式中:

w(n)=exp(jε(n))-1=x(n)+jz(n)

(19)

当SNR较高时,w(n)的实部和虚部根据泰勒级数展开进行一阶近似,有

(20)

z(n)=sin(ε(n))≅ε(n)

(21)

因此,与式(8)相对应的yp=[yp(1),yp(2),…,yp(N)]的条件概率密度可写为

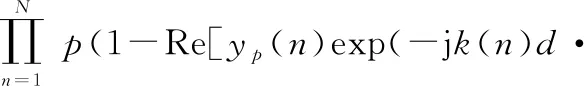
(22)

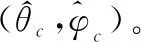
(23)

(24)

式中:round为四舍五入运算。然后通过模糊数即可计算出相位真值,即

(25)

3 理论精度下限分析

采用信噪比分析时变阵对频变目标的测向误差下限,作为评价时变阵测向性能的指标。由式(1)可得关于方位角和仰角的Fisher矩阵元素为

(26)

式中：α1=θp;α2=φp;μn=cos(φp(n));νn=sin(φp(n))。再根据式(5)得Fisher矩阵的各元素为

(27)

求Fisher矩阵的逆,即可得到合成圆阵测量宽带时变信号的方位角与仰角的克拉米劳精度下限,分别为

(28)

(29)

值得注意的是,若采样点均匀,各采样信号频率、SNR相同,分别为k0c/2π和SNR0时,可得到仰角、方位角的克拉米劳下限表达式,分别为

var(Δφp)≥(NM×SNR0)-1(k0dsinθp)-2

(30)

var(Δθp)≥(NM×SNR0)-1(k0dcosθp)-2

(31)

可见,来波入射角远离阵面法向,仰角测向误差增加,而方位角测向误差减小。同时,测量相位的采样点和场分布的采样点数越多、SNR越高,测向误差越小。

4 EM算法求解多信号参数

在多辐射源入射条件下,直接求解法既求下式的ML解：

(32)

式中：dis[x]=|mod(x,2π)|定义相位的距离,mod(x,2π)表示x对2π取余数运算。注意到,在信号未分选的情况下,尚无法确定相位值与辐射源的对应关系,以及辐射源的入射角,因此对式(32)的直接求解是一个计算复杂度为非确定性多项式的问题[37]。

换个角度,若已知辐射源的入射角信息,则可依据角度信息计算得到该辐射源在合成圆阵处产生的理论相位差,并将与该相位差最接近的采样数据来自该辐射源,以此进行信号分选,从而建立辐射源与采样数据之间的对应关系。另一方面,若已知信号分选,即已建立各接收数据与其辐射源辐的对应关系,则该P维问题变为P个一维问题,通过接收数据进行入射角解算。基于此将高维复杂问题降维的思想,本文先将观察数据进行随机分组,根据每组频率、幅度、相位差等数据分别进行单辐射源的入射角估计,然后根据估计的入射角对观测数据进行重新归类,并依次在估计和归类间进行迭代,直至算法收敛。合成阵列求解时变多目标参数的EM算法流程如图3所示,主要包含求期望值步骤和期望值最大化两个步骤。

4.1 求期望值步骤

求期望值步骤的作用是进行信号分选,即根据辐射源入射角计算该位置在合成圆阵处产生的相位差,并以采样相位差距此理论相位差最小为依据进行接收数据的重新分组,将的采样数据归为一组中。根据第p个辐射源第i次入射角估计值,其在合成圆阵处所产生的理论相位差为

(33)

根据每个观测相位差与理论相位差的距离,将观测相位差与理论相位差最接近的数据分为同一组,即

(34)

最终将观测数据分为P组。

4.2 期望值最大化步骤

此步骤采用ML法,通过分组后的观测数据分别计算每组数据对应的二维入射角,即将求期望值步骤中每组观测数据分别求解下式的ML解:

(35)

5 数值仿真实验

本节通过数值实验仿真分析无源合成圆阵的信号分选和测向性能,并验证求解时变多目标信号参数的EM算法的能力。

5.1 单辐射源情形

本节主要考察测向误差的均方根值随入射仰角的变化情况。两天线间距为1.2 m,旋转一周采样点数为100。信号的中心频率为1.5 GHz,频率变化范围为中心频率的13%,即从1.4～1.6 GHz范围内随机变化。SNR在-10～10 dB内随机分布。仿真采用的每个接收信号的SNR与来波频率如图4所示。

仰角从5°变化到75°,方位角固定为170°,分别进行500次独立计算,并将测向误差的均方根与CRLB进行对比,重点考察了考虑每个接收信号SNR不同的情形。计算结果对比如图5所示。考虑不同采样点的SNR能提高测向精度,且考虑SNR的测向精度接近理论误差下限。同时,入射仰角越大,方位角测向误差越小,仰角测向误差越大,与分析结论相符。

5.2 多辐射源情形

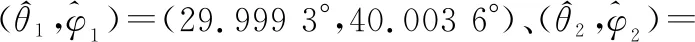
6 结 论

本文重点讨论了采用无源合成阵列在多辐射源环境下对时变信号的参数估计问题,包括对多个辐射源的二维测向以及对其产生交错信号的分选。建立了无源合成圆阵测向的数学模型,考虑了目标频变、测向位置非均匀、单次测量信噪比不同等因素。提出了采用无源合成阵列进行时变多信号参数估计与分选的EM算法。该算法通过将高维多参数估计问题分解成多个低维参数估计问题,从而降低运算复杂度。根据基于相位数据的ML估计方法,推导出闭合形式且性能接近最优估计的入射角计算解析解。此外,采用基于接收响应复数的ML方法,利用旋转带来的基线多样性实现了相位模糊的解算。通过两种不同似然方法的有机结合,兼顾了入射角初值计算运算量与最终入射角的求解精度。通过理论下限推导,分析了无源合成圆阵的测向精度,揭示了入射仰角、阵列口径、采样点数和信噪比对二维测向精度的影响。最后通过单辐射源和多辐射源的数值实验验证了分析结论和算法的有效性。