星载双基地雷达杂波抑制能力分析与构型优选

何鹏远, 杨志伟, 谭 啸

(西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)

0 引 言

天基单基雷达虽然具有运行轨迹确定、波束在地面覆盖范围广等优势,但容易受到蓄意干扰,同时其生存能力也受到了威胁。在此背景下双多基雷达应运而生并受到了广泛的关注。天基双基雷达接收卫无源,通过与发射星联合观测的设计,可使发射卫星不易被攻击,接收卫星不易被发现,具有抗隐身、抗反辐射导弹、抗综合电子干扰、抗超低空突防等优势,在实际应用中具有重要地位[1-6]。该系统还可以采用单发多收的组网观测形式,来实现全球成像、测绘与地面动目标检测等应用,如同步轨道-低轨道(geosynchronous earth orbit low earth orbit, GEO-LEO)构型的组网观测模式[7-8]。除此以外,双基系统同时还拥有多种工作方式,具有很大的应用潜力。

由于双基地收发分置,具有轨道构型差异大、空间尺度异构的特性,导致其分辨率、杂波特性均与单基地卫星具有较大差异[9-10]。首先,由于回波的多普勒由双基雷达与场景之间的相互运动产生,同一距离门的方位分辨率在不同的方位角相差较大[11-13],在不同方位的杂波存在不同程度的谱展宽。同时,杂波的空间频率仅由场景与接收基站之间空间锥角决定,这导致在同一环上的杂波空时谱不再呈现线性关系,杂波具有严重的距离依赖性,空时谱的弯曲程度越大,距离依赖性越强。当采用来自相邻距离门的数据作为当前距离门的训练样本时,会导致估计的杂波谱展宽,从而导致慢速目标淹没在杂波谱中。针对距离依赖性强的杂波通常采用对单距离门的样本进行估计,可从两方面入手,一类是直接数据域进行恢复,然而此类处理会使杂波的自由度降低,导致恢复的杂波谱不够稳健;另一类是通过稀疏恢复的算法,然而此类算法计算量大,工程实时处理[14-18]难度大。

针对以上问题,研究在不同轨道构型下的杂波谱特性,选择杂波距离依赖性较弱的区域,为将来的实际工程处理简化流程是很有必要的。本文结合星载双基几何构型,分析了地形起伏与分辨率空变对杂波结构的影响,建立了杂波协方差矩阵分析模型、抑制性能模型与空时谱结构分析模型。最终对同轨道高度下的类单基构型与非类单基构型的杂波空时谱结构与抑制能力进行了理论分析与仿真验证,为星载双基构型的构型与观测模式的选择提供了理论支撑。

1 信号模型

1.1 杂波信号模型

假设双基中接收卫星采用全孔径阵面,列向合成后有N个通道,通道间距为d,在相干积累时间(coherent processing interval, CPI)内以脉冲重复频率(pulse repetition frequency,PRF)为Fr发射了K个脉冲,则针对第l个距离门第p个分辨单元的杂波,根据文献[9]设其双基角为φ,则杂波p的多普勒频率ft(φ)与空域频率fs(φ)分别计算如下:

(1)

(2)

式中：下标“1”“2”分别代表发射与接收站,各矢量示意与符号如图1中所示；V代表在地惯坐标系下的速度矢量;P代表地心指向基站的矢量；R(φ)代表在双基参数角φ下由基站指向地面坐标的矢量；A为接收机阵面轴向指向；λ为波长；ωe代表地球自转的角速度矢量,实际处理中需考虑地球自转的影响。根据文献[13],可将地球自转的影响转移到卫星上,由自转产生的附加速度矢量即为惯性系下自转速度与位置矢量的外积,即引入了一个等效的偏航角,关于地球自转对空时谱的影响在文献[9]等均有分析,这里不再赘述。

在文献[9]中,杂波建模以椭圆参数角φ对杂波进行了等间距的划分,然而实际上,双基构型下来自不同的参数角φ所对应的分辨率并不相同。根据文献[11],杂波的距离与方位分辨率分别为

(3)

(4)

式中：B为系统带宽;c为光速;β为双基两距离矢量R1(φ)与R2(φ)间夹角;k1与k2分别为0.886的3 dB展宽系数与成像引入的展宽系数;T为积累时间G⊥为地面投影矩阵;ω1与ω2分别为发射机与接收机相对于地面点的运动角速度。忽略平台运动对脉压的影响并补偿平台运动引入的高次项后,来自于第n个通道,第k个脉冲时接收的第l个距离环的信号可以表示为

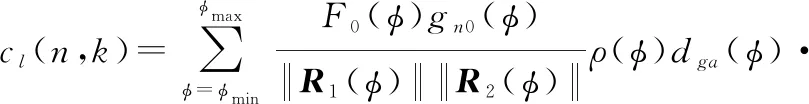
(5)

式中：ωs(φ)与ωt(φ)分别为fs(φ)与ft(φ)对应的角频率;F0(φ)与gn0(φ)分别为发射的与接收的合成方向图在φ方向的增益;ρ(φ)为对应角度的后向散射系数。

1.2 星载双基地雷达轨道与观测模型

本文针对同轨道高度星载双基雷达轨道构型与观测模型进行优选。根据轨道不同倾角构型,可将双基星载构型分为同轨道前后跟飞模型与轨道倾角差较大的任意轨道模型,其构型与观测模式如图2所示。

对于前后跟飞构型,主要分为3种观测模式进行优选,如图2(a)中a为同前/后侧观察;b为同外侧观察；c为同内侧观察。然而,对于观测区域a与观测区域c,系统将会产生多普勒模糊,不适合进行观测。对于任意轨道构型,如图2(b)中a为同向内侧，b、c为同向外侧观察。其中φ为椭圆参数角,RL为卫星至轨道交点的距离。本文主要针对杂波抑制能力研究在不同种构型下观测模式的优选,下面给出性能分析模型。

1.3 性能分析与距离空变分析模型

第l个距离环上散射点的数据叠加构成该距离门的一个回波脉冲数据,假设不存在目标信号,则由该距离环中多个角度下的杂波回波数据共同构成该距离环对应的空时两维数据:

xNK×1=[cl(1,1)，cl(2,1)，…,cl(N,1),…,
cl(1,K)…,cl(N,K)]T+n

(6)

式中：n为噪声向量。空时全维最优适应处理是空时自适应处理(space time adaptive processing, STAP)处理方法的理论效果的上限,因此这里采用全维最优处理权矢量进行输出加权,计算如下:

wopt=R-1S(ft,fs)/(SH(ft,fs)R-1S(ft,fs))

(7)

通常用输出信杂噪比(signal clutter nolse ratio, SCNR)损失(SCNR-Loss)衡量杂波抑制的性能。在信号、杂波与噪声互相独立的前提下,代入加权矢量,输出SCNR可计算为

(8)

(9)

Δe的含义为空时谱的空域频率对时域频率的二阶导数。需注意的是,为避免Δe过小,本文采用的是对归一化的ft进行求导,Δe大小与当前的PRF,轨道构型与观测模式有关,在不同的模式与参数下不能直接通过比较Δe的大小来评判性能。

2 影响因素分析

为对系统的杂波抑制能力进行分析与构型优选,需要对除构型与观测模式的其他因素进行分析考虑,避免由其他因素带来的影响。本节针对式(5)中关键的几个影响因素进行分析,包括地形起伏对二维频率的影响与双基合成方向图的影响。

2.1 地形起伏影响

由式(1)、式(2)可知,杂波谱与双基的构型与观测模式息息相关。同时,针对某一等距环,可能受到等距环后方的起伏地形影响,从而导致观测角度改变,进而影响杂波谱结构,如图3所示。下面对地形起伏对杂波影响进行理论分析。

如图4所示,以接收星为例,接收卫星的第一通道为坐标原点,建立卫星速度坐标系[7],设偏航角为γa,卫星高度为H,地球半径为Re,第n个通道的坐标为(dncosγa,dnsinγa,0)。设在双基角φ下,地形高度为h的杂波点相对于接收卫星的下视角为βh,方位角为φh,擦地角为ηh,角度关系可根据文献[9]中的双基中点坐标系进行求解,下文中对以上角度不再特意标注为φ的函数。

根据几何关系可以计算海拔高度为h的观测点Ph=(rhsinβhsinφh,rhsinβhsinφh,rhcosβh)则第n个通道相对于第一个通道的波程差Δr为

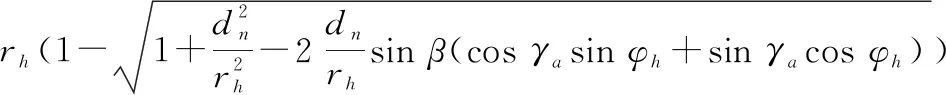
(10)

由于rh≫dn,对式(10)展开并补偿后有

Δr=dsinβh(cosγasinφh+sinγacosφh)

(11)

此时,杂波点在相邻通道间空域角频率差为

(12)

根据空间几何关系,将角度关系代入发射与接收卫星,最终总的多普勒角频率为

(13)

可以看出,当接收机偏航角γa=0时,空域频率中仅存在由下视角与方位角所合成的空间锥角的分量,当偏航角γa不为0时,会引入一个投影在接收机垂直航迹向上的分量,导致空域频率与多普勒频率非线性分布。然而可以预见,在双基构型下,地形的起伏对空时谱分布的影响很小。一方面,接收机星内的垂直基线很短,系统空域频率与接收机运动所引起的多普勒谱仍呈线性关系;另一方面,由于卫星照射距离通常在几百千米,对于发射机来说,几百米内的地形起伏对下视角β1h的变化很小,即由发射机所引起的多普勒变化很小。

2.2 方向图调制影响

双基模式下,天线阵面在经过列合成后,发射与接收的方向图分别计算如下:

(14)

(15)

式中:θ(φ)代表在双基角φ下,观测点相对卫星天线的空间锥角;θ10与θ20分别为发射/接收卫星的波束中心指向;D为天线阵面长度。可见,在双基模式下由于卫星的波束指向不同,会导致合成方向图的展宽,同一多普勒单元幅度受到复杂调制,杂波自由度变多,从而导致杂波抑制能力可能的下降。但当距离的空变性变化不大时,即使方向图存在展宽,对系统的杂波抑制能力也影响较小。

综上分析可知,在双基模型下,地形高度起伏与方向图对杂波抑制的影响较小,主要影响杂波抑制能力的仍是杂波的距离空变性。

3 仿真实验及分析

本文在建立的杂波模型基础上,重点对不同轨道构型与观测模式下的杂波距离依赖性进行讨论。在同轨道高度双基构型下主要可分为同轨道高度任意轨道构型与同轨道前后跟飞构型。在同轨道前后跟飞的基础上又可分为长基线跟飞构型与类单基构型。下面分别进行实验分析。

本文首先引入类单基构型的定义。根据双基地模型,当双星位置重合在一起时,等距离和环将退化成为圆,与单基所形成的正圆重合。然而,随着轨道倾角的微小偏移、两星之间的距离的增加,由两星形成的等距离和环的离心率升高,等距离环的椭圆将不再与单基的等距离环重合,并且距离越长,越靠近椭圆长轴,偏移越大,如图5所示。因此,本文规定在一定双基参数角φ范围内,双基等距环与单基等距环的距离差ΔR不超过半距离分辨率,即可认为是类单基构型。

由于双基距离环与单基几乎重合,离心率接近于0,并且两星速度大小相同,当φ在一定的小角度范围内,式(13)可改写为

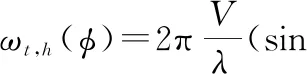
(16)

假设偏航角γa=0,由于类单基距离相近,此时θ2与φh几乎相同,即

(17)

可见当φ在一定的小角度范围内的类单基构型下,杂波直接采用双基参数角φ进行计算会大大简化处理流程,并且地形的起伏不影响杂波空时谱结构。

下面对类单基构型的约束进行实验分析。假设双基轨道高度均为632 km,双基参数角所允许的范围为45°～135°, 在观测中心的入射角分别为20°,30°,40°,带宽20 MHz。斜距误差与距离分辨率的比值曲线如图6所示。可见,在此高度下,随着入射角的增加,观测距离越远,对星间距离的约束越大。以入射角40°为例,星间距离最大只允许至5 km。

图7给出类单基的杂波空时谱曲线变化情况,图8为单基与类单基的输出SCNR曲线,轨道参数如表1所示,星间距为5 km,N=K=16,系统带宽为20 MHz,载频为1.3 GHz,脉冲重频Fr为5 kHz,阵元间距为半波长。其中,双基参数角范围为89°～91°,即处于正侧视照射情况。忽略地球自转的影响,不同距离下的空时谱几乎重合,可见类单基空时谱与单基空时谱类似,不具有距离空变性。因此对于类单基构型,为避免发生多普勒模糊,应向正侧方向进行观察。

表1 类单基卫星轨道参数

4 长基线前后跟飞构型

将星间基线逐渐拉长,双基构型将从类单基构型转化为长基线跟飞构型。空间基线越长,发射机的所引入的多普勒越分布不均匀,导致空时谱弯曲程度越大。在表1的实验参数下,修改星2的近地点幅角来修改星间基线距离,图9给出了φ为0°～180°时理论空时谱曲线,可以看出随着星间距离的增加距离弯曲程度增加。并且在观测区域靠近于前后视观察区域,即空时谱图中多普勒绝对值较大区域,可看出其距离弯曲程度同样在增加,相比于正侧区域距离空变性强。

更进一步,对输出SCNR的凹口宽度进行分析从而完成上述距离空变性的验证。图10给出在上述试验参数下从类单基构型过度至长基线构型,向两星正外侧观察,双基角γ=60°,φ=90°[9]时Δe随星间距离的改变情况与输出SCNR曲线凹口展宽情况。可以看出,随着星间距的增加,杂波的距离空变性在变高。如果要求输出SCNR-Loss凹口展宽程度不超过5%,即对应MDV损失不超过5%,则要求星间距小于180 km。图11出了地形起伏对杂波谱曲线的影响的局部放大图,其中地形起伏满足平均高度200 m,方差100 m的高斯分布。由结果可见,在双基情况下,地形起伏的影响非常小,与理论分析一致。

5 任意轨道构型

针对同一高度任意轨道构型,为保证较高的时空覆盖能力,通常使卫星轨道相近,飞行方向平行。由几何关系可知,当两星距轨道交点的距离RL相等时,不同观测区域与双基卫星的空时频率的分析关系相同,只为双基距离2a与双基角度φ的函数,为便于分析,使两卫星位置距轨道交点距离相等,接收星的天线阵面轴向平行于接收星运动方向,如图2(b)所示。后续试验轨道参数如表2所示。对于任意轨道构型,在上述条件约束下,主要研究星间的轨道倾角差与不同观测区域之间的杂波距离空变性与抑制能力。

表2 试验2卫星轨道参数

一方面,不同的观测模式会对杂波的分布产生影响。首先对轨道倾角差固定时不同观测区域之间的杂波距离空变性进行分析。为避免卫星间距过近,图12给出了在轨道倾角差为10°时,近地点幅角均为10°,不同距离环下的理论DD-Curve (direction Doppler Curve),φ=90°附近曲线发生了折叠,并且根据不同距离环的空时谱可发现在折叠处空时谱差异最大,可见其在此出距离空变性最强。其中,空时谱折叠区域对应同向内侧观察区域。

为进一步验证上述仿真的距离空变性问题,下面在输出SCNR曲线对系统的距离空变性进行验证。设输入信噪比与杂噪比均为30 dB,Fr为5 000 Hz,图13给出了该构型下不同双基参数角下的输出SCNR曲线。可见,图13验证了图12的仿真结果,可知在向内侧观察时其输出SCNR-Loss曲线凹口较宽,检测性能很差,相反,在两轨道外侧可以获得较窄的凹口,检测性能较高。另一方面,双星的轨道倾角差也会对杂波的距离空变性产生影响。由之前分析可知,对于内侧时谱折叠区域,距离空变性极强,因此不对此区域进行分析,仅针对向接收星外侧进行观察时分析Δe的变化情况,仿真结果如图14,可以从结果得出,随着轨道倾角差的增大,双基构型由类单基构型过度至任意轨道构型,杂波的距离空变性在增强。

最终,图15给出了前后跟飞构型下星间基线200 km时采用双基合成收发方向图与单基收发合成方向图的结果。设收发天线方位向宽度均为10 m,距离向宽度为1 m,阵元间距为半波长。波束中心均指向φ=90°,γ=60°,可以看出由于双基的波束方向图存在展宽,导致输出SCNR曲线凹口展宽,检测性能下降。然而不难得出当杂波的距离空变性较弱时,由方向图所引入的杂波谱展宽将会下降。

6 结 论

本文综合考虑了地形起伏、方向图调制、星间基线等对杂波的影响,系统建立了星载双基杂波模型,并建立了空时谱弯曲率Δe的距离依赖性分析模型与SCNR-Loss抑制性能分析模型,最终对同轨道高度的类单基模型与非类单基模型分别进行了理论分析与仿真验证,结果表明:

(1) 对于类单基构型,其空时谱曲线与单基模型类似,距离依赖性低,输出信杂噪比曲线凹口较窄,可以获得更好的检测性能。

(2) 对于非类单基模型,星间距的增加会导致椭圆离心率的增加,使得空时谱曲线弯曲程度增加,即距离依赖性增强。而双星的运行方向相差越大,距离依赖性越强。观测区域方面,应向两星轨道的外侧观察。