基于单站干涉仪测向法的未知辐射源定位技术*

韦 卓

（中国兵器工业试验测试研究院 华阴 714200）

1 引言

信息化武器装备在靶场进行设计性能及指标检验时，需排除一切未知干扰因素对检测结果的影响，其中最为关键的是排除一切未知电磁信号，尤其是同频、临近频率的电磁信号。但是由于靶场是一个开放的试验空间，在试验时难以保证试验区域的电磁环境纯净，因此试前、试中需对试验区域电磁环境进行监测采集，一旦发现与被试装备所用频段有重合或邻近的未知电磁信号，需要查找该信号的辐射源位置，协调关闭该辐射源，保证试验的正常进行。

但是目前技术成熟的单台无源监测设备在静止状态下以采集分析信号参数及测向功能为主，对未知辐射源不具备定位能力［1］。针对这一问题，本文采用单台无源监测设备多次布站的方式，通过测向交叉定位法及误差剔除方法，可较为精确地得出辐射源的位置坐标［2～5］。

2 干涉仪法测向原理

采用单台无源监测设备对辐射源进行定位，首先需要测得辐射源的来向。对辐射源测向的方法较多，有干涉仪测向、比幅测向、空间谱估计等多种方法，其中干涉仪测向法因测向精度高、速度快等特点，广泛应用于靶场对未知辐射源的测向中。干涉仪测向是利用测量同一辐射源到达接收天线阵列的各单元之间的相位差来确定辐射源来向的一种测向体制［6～8］，测向示意图如图1所示。

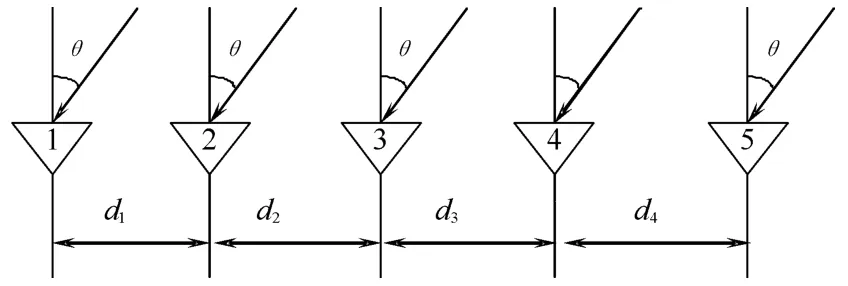
图1 干涉仪法测向示意图

两天线的接收相位误差为

则通过式（1）可得，辐射源的来向θ，如式（2）所示。

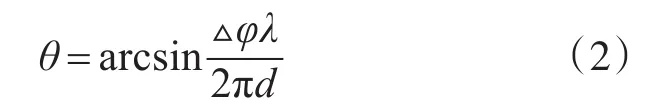
其中：Δφ为两天线测得的辐射源相位差；θ为辐射源入射角；d为两天线之间距离。

根据数字干涉仪测向原理，其不模糊视角为

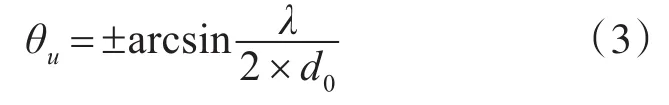
其中：θu为不模糊视角；λ为侦察信号波长；d0为虚拟短基线长度。

数字干涉仪测角误差公式如下：

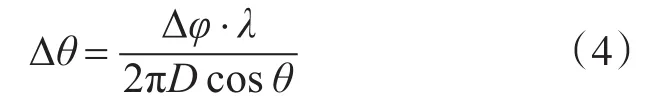
式中：Δφ为两天线测得的辐射源相位差；D为天线阵总基线长度；λ为侦察信号波长；θ为辐射源入射角。

通过分析式（3）、式（4）可见，在信号波长一致的情况下，干涉仪测向法不模糊视角与测向精度是矛盾的，天线基线越短，不模糊视角越大；天线基线越长，测向精度越高。为了解决这一矛盾，一般采取多基线法布设天线阵列，短基线保证较大的不模糊视角，长基线保证测向精度［9］，同时可采用四面阵天线，保证所有来向信号都在天线的±45°范围内，进一步保证信号不会处于不模糊视角外，且保证信号的测向精度。四面阵多天线布局示意图如图2所示，天线接收方向如图3所示。

图2 四面阵多天线布局示意图

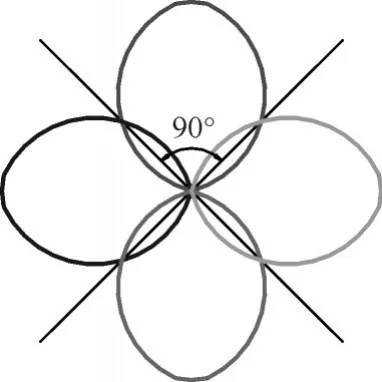
图3 四面阵天线接收方向图

3 定位原理

单台电磁无源测向设备可测得自身所在位置坐标及辐射源来向，采用交叉定位法可实现对辐射源的初步定位。交叉定位法是在已知的两个或多个不同位置上测量辐射源电磁波的到达方向，然后利用三角几何关系计算出辐射源位置。具体实施办法是：1）将无源测向设备布在一个选定位置，利用设备本身自带的GPS/BD测向定位装置测出布站坐标（x1，y1），利用电磁无源测向设备测出辐射源以该站为原点与正北方向的夹角a1；2）将电磁无源测向设备重新布站，为了保证计算精度，要求两个站之间的距离≮3km［10］。在新站址重新测量电磁环境监测设备的坐标（x2，y2）以及辐射源以该站为原点与正北方向的夹角a2。利用电磁环境监测设备两次布站测得的其本身坐标（x1，y1）、（x2，y2）和两个辐射源与正被方向的夹角a1、a2，采用交叉定位法可以计算辐射源的坐标（p，q），交叉定位法原理图如图4所示，计算公式如下所示。

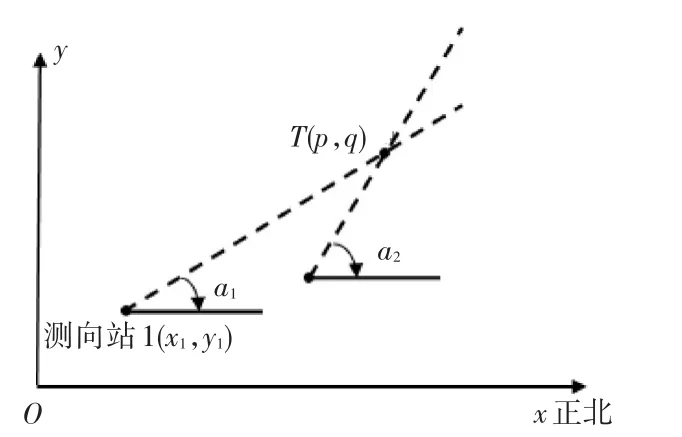
图4 交叉定位法原理图

根据角度定义可以得到：

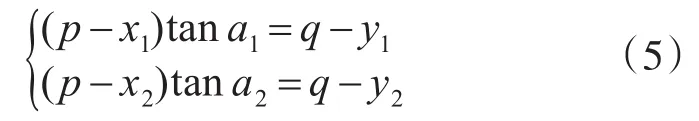
解方程组（5），可得辐射源的位置坐标为

电磁无源测向设备要求是按规定日期校准过的，因此不考虑其测量本身站点坐标和辐射源方位存在系统误差，但是需要考虑测量的随机误差，该随机误差通过式（6）的计算结果传导进辐射源的坐标（p，q）上。从统计学和概率学上讲，最有效的一种减小随机误差的方法是多次测量然后取平均数，然后剔除误差较大的野值，再取平均数的方法，增加辐射源坐标测量精度［11～12］。

假设通过多次布站和交叉定位计算，得出n个辐射源的坐标，记为

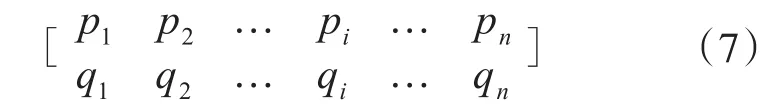
式（7）中第一行代表计算得出的辐射源的横坐标，第二行代表计算得出的辐射源的纵坐标。

对式（7）中辐射源的横坐标和纵坐标分别取平均值，记为

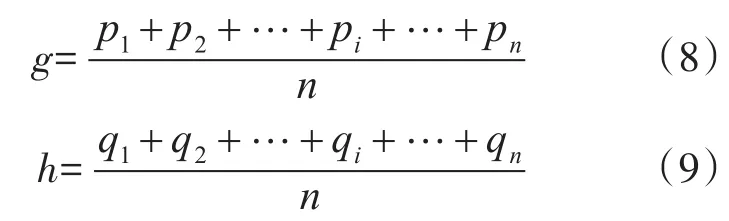
为了进一步提高精度，采用两点之间距离公式，将式（7）中的坐标与式（8）、（9）取平均值后的坐标（g，h）分别计算距离，得到（L1，L2，…，Li，…，Ln），对这n个距离取平均值，记为

将计算得到的n个距离值（L1，L2，…，Li，…，Ln）与式（10）的L值进行比较，大于L值的认为是野值，剔除掉其对应的坐标点位，剩下的m个坐标点位再使用平均数公式进行计算，记为

式（11）、式（12）计算的辐射源坐标（J，K）即为最终得出的精度较高的辐射源坐标值，计算效果图如图5所示。

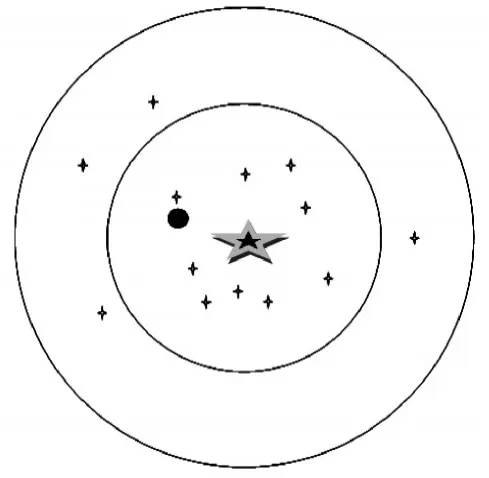
图5 平均数法计算辐射源坐标效果图

其中黑色小十字标代表采用交叉定位法计算的未知辐射源的位置坐标（p，q），圆形黑点代表采用式（4）、式（5）计算的辐射源平均位置坐标（g，h），圆环中十字标代表需要剔除的误差较大的野值，小圆圈代表剔除测量野值之后剩余的辐射源范围，五角星代表剔除野值之后，利用小圆中剩余的辐射源，采用式（11）、式（12）计算得到的最终较为精确的辐射源位置坐标（J，K）。

4 结语

本文选用干涉仪测向方法，保证了对未知辐射源的测向精度。通过测向设备多次布站测量的方法，实现了基于辐射源来向的交叉定位，很大程度上保障了信息化装备科研试验的正常进行。但是该方法目前仅适用于对地面固定辐射源进行定位，对移动目标不具备定位能力。考虑到靶场试验中未知辐射源主要来源于地面，该方法是一种比较简单实用的技术手段，但对于来自空中的未知辐射源，该方法还不具备定位能力，有一定的局限性，还需要国内相关院所展开进一步研究。