基于遗传算法的多波次攻击下舰船弹性优化*

田 璐 李 震 詹梦园 苗 虹

（1.江苏科技大学电子信息学院 镇江 212100）（2.江苏科技大学经济管理学院 镇江 212100）

1 引言

高新技术发展迅速，战争形态已演变成五位一体的联合作战，包括海、陆、空、天、电磁［1］。因此，多波次同类型甚至多波次多类型的攻击方式成为海上常用作战方式之一。由美国国防部提出并得到广泛认可的弹性系统定义是：一个弹性系统无论在什么环境下都能很好地发挥节点效能［2］，有通过重新配置或更替并与其他系统相适配的能力，并且具有适度的和可知的效能下降。在多波次的作战环境下，系统面对的不仅仅是一次毁伤，而是多次毁伤，系统弹性不止体现在受到攻击后恢复，这是略显被动的，应更主动地去减少在多波次毁伤中受损。

2 基本概念和方法

2.1 弹性系统及其恢复

从工程角度来看，弹性已被作为系统的一个重要属性去看待，即系统受到攻击导致系统物理损坏或超出其抵御能力范围之后，并能够从受损状态恢复其基本功能的能力。系统弹性指的是在破坏事件发生后系统对损失的性能进行恢复的能力［3］。一个优良的恢复策略可以使系统在受到扰动后的一定时间内恢复到最佳的性能水平，恢复方式主要分两种：外在的装备修复与内在的重组。

修复是对破坏组件进行维修、修复或替换。维修是为使系统保持、恢复或改善其规定技术状态所进行的全部活动［4］。因此，维修策略的制定是重中之重，一个完好的军事系统维修策略可以使己方经济、人员以及战备物资损失最小化，并且重新掌握战场的主动权。事实证明，在先进信息技术条件下的小区域战争中，备战条件被压缩，战争进程大幅加快，保持部队战斗力将更加依赖于防御系统的维修保障。

2.2 商弹性模型

系统弹性定义为系统节点效能的恢复值与损失值的比值，即利用恢复的节点效能水平与降低的效能水平的比来度量弹性变化［5］：

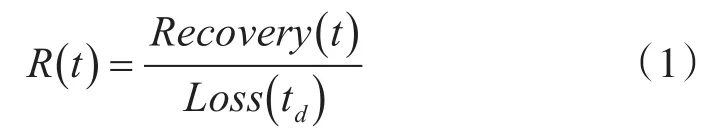
式中：R(t)为t时刻系统弹性，称为商弹性模型，Recovery(t)为t时刻恢复的节点效能水平，Loss(td)为系统节点效能的损失值。式（1）展示了系统从干扰事件中恢复的能力。如果系统能恢复到初始状态，即Recovery(t)=Loss(td)，那么系统具有完全弹性；相反如果无恢复值，即Recovery(t)=0，那么系统便没有表现出弹性。

给定性能度量φ(t)、干扰事件ej、干扰事件发生时间te、恢复开始时间ts、恢复完成时间tf时，整个性能变化过程中系统弹性，可以用如下的公式来表示：

式中：RQ(t|ej)为干扰事件ej发生后t时刻系统的商弹性，φ(t|ej)为t时刻系统的性能，φ(td|ej)为干扰事件ej下系统退化后的性能。式（2）中分母表示的是干扰事件发生后系统性能的退化程度，其值越小弹性越好；分子表示的是在恢复策略作用下系统所能恢复的性能水平，其值愈大弹性越好。分子和分母的值分别反映了弹性过程中干扰事件和恢复策略两要素对系统性能的影响。

2.3 MTSP问题与遗传算法

MTSP问题属于NP-hard组合优化问题［6］，具有离散、分组并行和多目标优化的特点，使得启发式算法在MTSP问题上得到了广泛应用［7］。Trigui［8］等将多机器人任务分配问题看作MTSP模型，以最大行驶距离和总行驶距离为优化目标，将多目标优化转为单目标优化问题；张美燕等［9］求解水下AUV路径规划问题时，将能量消耗和能量均衡作为多旅行商问题的双重代价，运用MTSP-GA算法模型输出三维坐标下的AUV路径。

遗传算法（Genetic Algorithm，GA）的理论基于进化论与遗传学说。进化论中的自然选择学说表示物种的产生是自然选择的必然结果。适应环境能力较强的个体才能存活并去繁衍后代，而适应环境能力较弱的个体则将被淘汰。王荣［10］利用遗传算法对变电站故障恢复问题进行求解，以设备操作代价、非故障失电区域最小为目标获取合理的开关操作表，完成故障区域隔离及非故障停电区域正常供电。蒋燕君和姜建国［11］对舰船电力系统故障进行研究，提出了一种基于云理论自适应GA的恢复策略，该方法将负荷与开关按优先级划分为多个目标函数，并考虑线路负荷分配均衡目标，用层次分析法整合成综合目标函数，再采用云理论自适应遗传算法来求解该模型。

3 系统模型建立

3.1 敌方攻击建模

海上攻击模式众多，本研究根据武器爆炸当量和拦截难度的从小到大依次选择了低空中的小型无人机、高空中的飞机/导弹以及水下的鱼雷三种攻击类型作为模拟对象，根据不同的攻击类型，构建多波次包含不同爆炸当量及落点的敌方攻击矩阵。本研究拟定敌方发动5波次攻击，攻击间隔为30min，每波次含有未知种类的攻击，如以下矩阵所示。

上式中Tn代表n波攻击，包括攻击序号、攻击当量以及攻击落点信息；攻击的序号n决定了攻击类型，1～10为高空飞机/导弹，11～20为低空无人机，21～30为水下鱼雷。

3.2 舰船防御系统

舰船防御系统包括系统节点的三维坐标以及节点类型，本研究为满足不同作战环境下节点重要度不同的这一理念，根据节点类型分配了不同战时任务，并建立不同作战环境下的不同重要度，节点信息见表1。

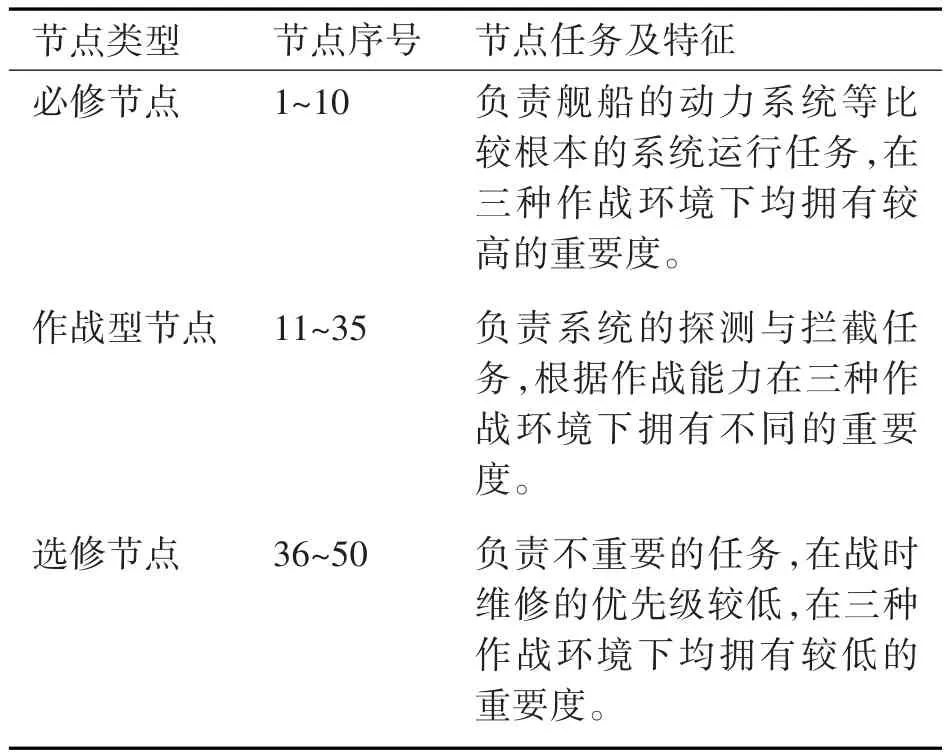
表1 节点信息表

作战型节点指可以对敌方攻击进行探测和拦截的装备节点；其探测概率（或拦截概率）单独给出，循环判断该波次的所有攻击是否拦截成功，部分作战型节点信息如表2。

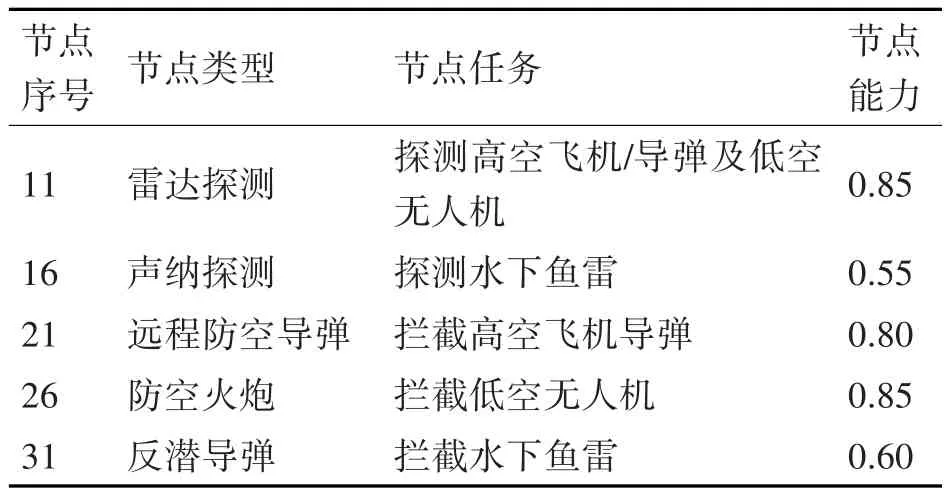
表2 部分作战型节点信息表

为更好地描述战时系统节点的损伤与修复情况，引入系统节点的效能等级矩阵E。装备节点分别具有6个效能状态，由低到高分别由0～5来表示，5级为最高级，表示节点完好，有100%的作战能力来抵御攻击；0级为最低，表示节点已损坏，节点效能为0%，即已经完全没有能力去完成拦截任务；舰船遭受攻击后，装备的效能等级根据毁伤程度等级进行相应的减少，并经过一定的维修后使节点的效能等级恢复一定的值甚至完全恢复至最高。4、3、2、1级分别表示节点基本无损伤、轻度损伤、中等损伤以及严重损伤，也使得节点效能为完好状态的80%，60%，40%，20%；效能等级矩阵表示50个节点的当前效能等级，初始均为5，若遭受到毁伤后，新的效能等级矩阵等于原效能等级矩阵减去毁伤矩阵。

3.3 爆炸毁伤模型

舰船在受到敌方攻击后系统节点遭受毁伤，为描述节点受毁程度引入系统节点毁伤矩阵EDestroy。每波次攻击开始时，先确定当前波次的攻防情况，再基于冲击波超压公式［12］，根据突防成功的敌方攻击的WTNT（TNT当量）以及落点确定防御系统各节点的毁伤程度，累加得到毁伤矩阵。系统节点的毁伤程度不仅与爆炸源的WTNT和中心位置有关，还与作战型节点的当前效能等级有关；故装备遭受的毁伤程度是关于毁伤半径、当前毁伤恢复程度的多元函数。冲击波超压ΔP见式（5）：

式中R'为等效距离，R为装备节点距离爆炸中心距离。为描述多波次攻击对效能等级的影响，当前效能等级的数学模型如下，表示为上一状态的效能等级矩阵与当前毁伤矩阵的差：

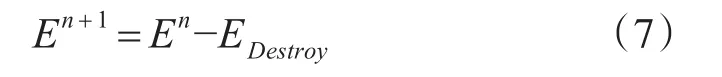
4 恢复策略及算法原理

文章研究讨论的是舰船在战时紧急情况下面对多波次攻击的最优维修策略问题；针对不同的战场环境，提出了攻击防御恢复策略（Attack Defense Recovery Strategy，ADRS），具体是指在单波次维修中，根据敌方攻击的类型确定装备节点的战时重要度，即明确不同类型的节点应对不同攻击的重要度，使得算法输出的维修序列更倾向于可以抵抗下波次攻击的装备节点。一般恢复策略是指在非战斗状态下，系统装备节点根据固定的重要度进行维修，并不区分节点类型与节点任务，ADRS相比较一般恢复策略能更有效地提高作战系统战时的自适应能力。

本研究将有限时间内多约束的多组并行维修序列问题拟成MTSP问题，将需要维修的n个装备节点比作多旅行商问题中的n个城市，m个维修小组并行维修与m个旅行商分别出发访问不同城市相对应。约束分为时间约束、维修备件的约束、维修人员数的约束，维修策略的数学模型可以描述为已知系统在受到干扰后，共有n个节点需要维修，不同节点设备需要若干个A，B，C三种类型零件，有S组维修人员共同去完成此次维修任务，每组携带若干A，B，C三种零件从不同受损节点出发，即每个节点的出度为1，在有限时间内分别去不同的受损节点进行维修恢复，每个节点被维修一次，即每个节点入度也为1，模型目标是寻找一种在有限时间和有限备件内可以让S组维修人员维修完成的节点重要度最高的维修路径，如式（8）和式（9）所示。

其中，totaldegree表示所有维修小组维修的总节点战时重要度。S表示维修小组数，degreei表示维修小组i维修子路径对应的总节点战时重要度，n表示对应维修小组维修最后一个节点的索引，Z[p(k)]表示当前作战状态下第k个节点的节点战时重要度。

为更好地描述节点的维修代价，引入每个节点的维修时间矩阵，维修时间由所需备件的数量加权后与装备节点当前效能等级相乘决定，如式（10）所示：

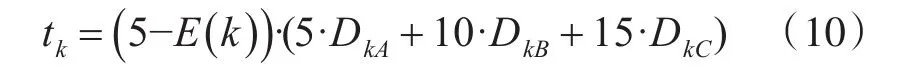
等式的右边分两部分。第一部分表示为节点k当前所缺的效能等级，等式的右边表示恢复一个效能等级所需要的时间。其中，Dk*分别表示第k个节点恢复一个效能等级所需的*种零件数量。

本研究利用传统遗传算法，通过交叉、变异操作输出最优维修序列。在每波次攻击结束后，为遗传算法提供对应战场环境的节点战时重要度值，使遗传算法在计算时倾向于得到更有利于下一波次对抗任务的种群适应度值。根据需要维修的节点数自适应调整基因序列长度，在有限时间、有限备件内得到使所有维修小组维修节点的总任务重要度最高的维修序列，并记录当前波次的恢复矩阵ERecovery，并将恢复矩阵与当前效能等级矩阵En相加得到新的效能等级矩阵En+1，表示为式（11）：

5 系统仿真与分析

本研究在敌方多波次的攻击下，使用商弹性模型从系统的恢复能力讨论其弹性，系统在战斗时尽可能的少受到攻击，使战斗结束时尽可能地恢复至最佳新能水平。系统弹性R的表达式如式（12）：

式中，n为敌方攻击波次，Recovery与Loss分别表示为所有波次中恢复矩阵与毁伤矩阵的和。为方便对照实验，固定作战型装备节点的探测/拦截概率、敌方攻击的打击概率等变量，仅改变算法运行中使用的装备节点重要度矩阵，对比分析在不同作战环境下ADRS相比一般恢复策略的优势。

1）多波次攻击均为无人机攻击

无人机攻击代表的是低毁伤、易拦截的攻击方式，当所有攻击均为无人机时，系统弹性过程如图1所示，因为毁伤小拦截难度低，因此对系统的维修并没有造成压力，在多约束条件下可以全部修好。系统弹性R为1，但是可以看到在经过第一波的维修后，第二波所遭受的毁伤有所下降，可以使得系统保持在一个较高的效能水平，因此可看出ADRS略优于一般恢复策略。

图1 多波次无人机攻击下系统弹性

2）多波次均为飞机/导弹攻击

飞机/导弹代表毁伤与拦截难度均适中的敌方攻击方式，当所有攻击均为飞机/导弹时，系统弹性过程如图2所示，因为毁伤与拦截难度也并没有很高，因此系统也可以逐渐在后续波次中恢复过来。系统弹性R为1，但是可以看到在经过第一波的维修后，第二波所遭受的毁伤明显下降，可以使得系统保持在一个较高的效能水平，因此可看出ADRS略优于一般恢复策略。

图2 多波次飞机/导弹攻击下系统弹性

3）多波次攻击均为鱼雷攻击

鱼雷代表毁伤高、拦截难度大的攻击方式，当5波攻击均为水下鱼雷攻击时，系统弹性过程如图3所示，可以明显看出，高毁伤的攻击方式可以使系统遭受巨大的冲击，每波次系统仅能修复一定效能等级数量的节点，因此一般恢复策略下系统尽管修复了大部分节点，但是仍无法有效避免下一波次的攻击，系统依旧遭受到毁伤；基于ADRS的系统在第三波时明显有有效的性能水平，使得该波次下受到毁伤减小，并在后续的波次中成功抵御攻击，将系统恢复至最佳性能状态，因此可以看出在此作战环境下ADRS大大优于一般恢复策略。

图3 多波次鱼雷攻击下系统弹性

6 结语

本研究讨论的是在多波次攻击下系统弹性的优化，从系统的鲁棒性角度去分析系统弹性。首先从毁伤程度与拦截难度的角度去模拟了不同类别的敌方攻击，构建敌我双方的对抗毁伤模型；然后基于遗传算法，多波次攻击下灵活调整基因序列长度，多次交叉变异输出节点维修序列；最后仿真并分析不同作战环境下ADRS相比较一般恢复策略的优势与劣势，结果表明：在探测与拦截难度大，毁伤程度高的作战环境下，导致对抗任务变得困难，维修任务艰巨，所以在有限的时间内当维修策略侧重维修作战类型节点时，可以有效地减少系统损伤，因此ADRS的优势较明显。当作战环境并不恶劣时，在规定时间内系统能维修完几乎所有损坏的节点，有时候即使不是最佳性能状态也不影响对下波次攻击的拦截，所以ADRS的弹性优化效果并不明显，但从系统鲁棒性去分析均可体现出ADRS的优势。