基于改进型差分进化的MLAT系统布站方法研究

胥松寿 ，郭歆莹

（1.民航河南空管分局 技术保障部，河南 郑州 450000；2.河南工业大学 信息科学与工程学院，河南 郑州 450000）

0 引言

场面多点定位（Multilateration，MLAT）系统是一种新式机场场面监视技术，通过计算目标发射信号到达地面中心站和基站的时间差（Time Difference of Arrival，TDOA）来计算其空间位置。系统的目标定位精度除了与伪距测量误差有关外，还受基站的几何布局影响。传统的布站多采用三角形、菱形、Y 形等，此种布站形式受基线长度和人为主观因素等的影响[1-5]。本文将差分进化算法应用于多点定位系统的最优布站设计，通过不断迭代计算来获得地面基站的最优布站位置。本文对差分进化算法进行了适当改进，使其在搜索前期有较强的全局探索能力，在后期有较强的局部开发能力，使之应用于多点定位系统站点布局设计的工程优化问题中，提高了系统定位精度对目标位置变化的鲁棒性。实验仿真表明，该布站设计方法在多点定位系统中可获得较高的定位精度。

1 基于改进型DE的布站方法

差分进化（Differential Evolution，DE）算法为求解切比雪夫多项式的问题，Rainer Storn 和Kenneth Price在1995年提出的经典优化算法。此算法是一种在连续空间进行随机搜索的优化算法，其优点主要体现在涉及参数少、算法简单有效、搜索过程随机、有助于理解和实现。经典的DE 算法始于种群的随机初始化，然后分别经过变异（Mutation）、交叉（Crossover）、选择（Selection）操作产生新一代种群，迭代进行该过程，直到满足停止条件[6-10]。

针对多点定位系统的最优布站问题，本文对经典DE算法进行适当改进，平衡了算法的全局搜索和局部开发能力，流程主要包括参数设置、种群初始化、改进的变异操作、交叉操作和改进的选择操作。

1.1 参数设置

参数设置对优化算法的性能和效率有很大的影响，针对特定的优化问题，应根据实际情况，设定理想的控制参数。改进型DE 算法涉及的控制参数主要为：种群规模NP、种群个体的维度D、尺度因子F 和交叉因子Cr 等。

1.2 参种群初始化

1.3 改进的变异操作

1.4 交叉操作

1.5 改进的选择操作

1.6 适应度函数

多点定位系统是一种利用双曲线/面定位的技术，根据目标到达地面中心站和基站的到达时间差TDOA 定位目标位置。系统的定位精度取决于TDOA 测量误差和站点布局，如式（7）所示：

式中，Δs为机场第s 个小区域定位精度，其中s∈{1，2，…，M}，M 为场面区域等分为若干小区域的个数，进而可计算每个小区域的定位精度；ΔTDOA为多点定位系统的TDOA 测量误差，与系统性能和时钟测量有关，系统搭建完场后，此参数基本保持固定；Gs为第s 个小区域几何精度因子（GDOP），由站点布局决定[15-16]。

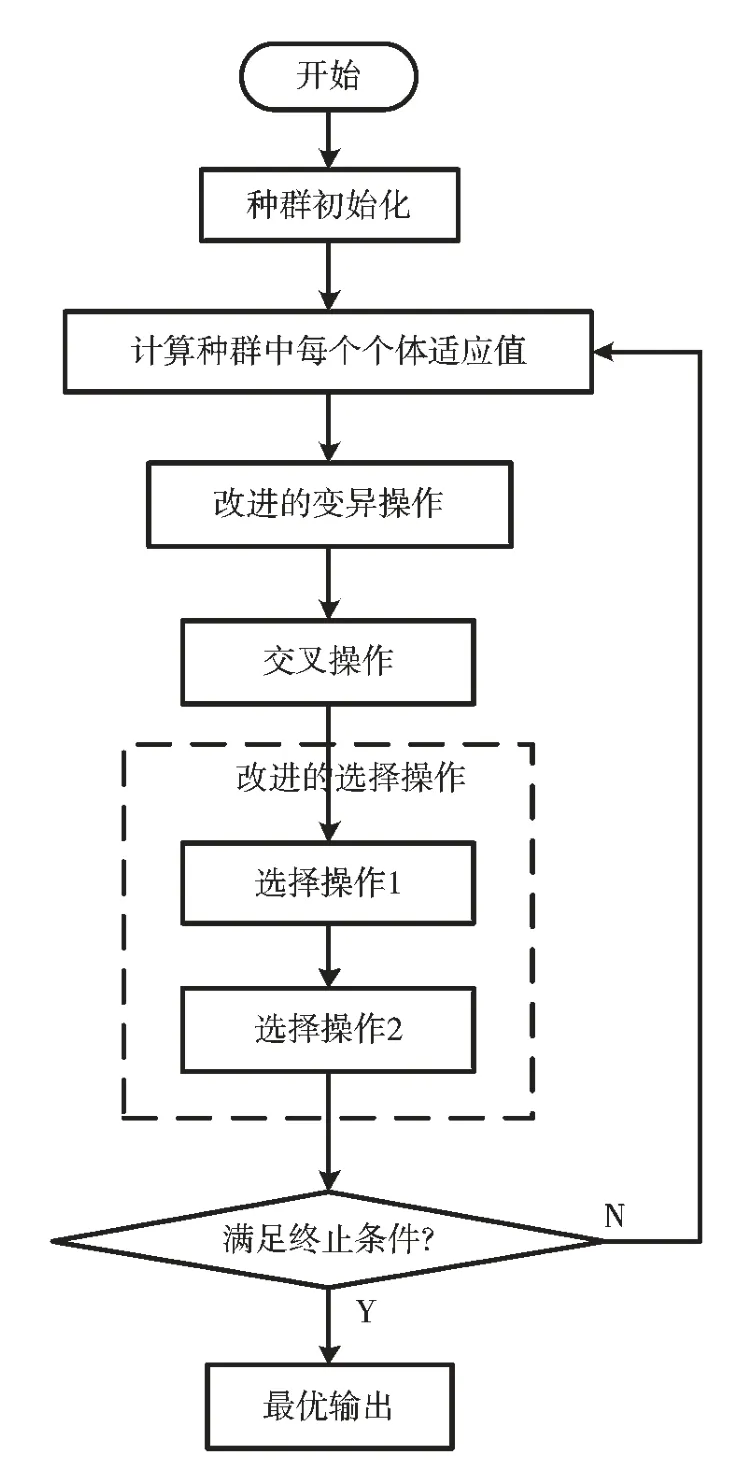
图1 改进型DE 算法流程图

由式（7）可知，Gs直接影响系统的定位精度，因此如何降低Gs值对系统的定位精度非常重要。基于此，本文以GDOP 为数据支撑，以最小化Gs值为优化目标，定义适应度函数如式（8）所示：

式中，M 表示场面区域等分为若干小区域的个数。因此本文以最小化适应度函数f 为目标进行优化，搜索区域内地面基站的最优布站位置。

2 仿真与分析

仿真条件：GDOP 计算区域大小设定为1 000 m×1 000 m，布站的搜索区域设定为1 000 m×1 000 m，基站高度搜索区域为[0，50]，单位为m，将GDOP 计算区域等分为为10 m×10 m的小区域，计算每块小区域中心的GDOP 值，累加计算适应度函数的值。设定种群规模NP大小为50，迭代次数I 为100 次。

2.1 最优布站和传统布站的定位精度分析

仿真条件：设定站点数量为4，其中1 个中心站，3个基站，因此种群个体的维度D=10，目标高度设定为50 m。传统布站采用倒三角和星型布站，具体的站点坐标和最优化站点坐标及对应布站方法的适应度值如表1所示。

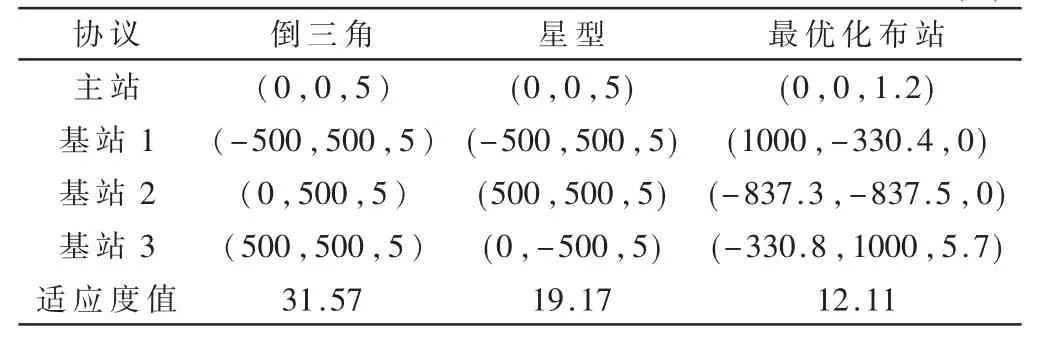
表1 站址坐标 （m）

由表1 可知，相比于传统布站方法，最优化布站方法搜索的基站坐标呈不规则分布且定位精度得到了较大的提高。

图2 给出了改进型DE 算法（IDE）和两种不同变异方案（DE/rand/1/bin 和DE/best/2/bin）的适应度值进化曲线。

由图2 可知，在进化的开始阶段，改进型DE 算法（IDE）与DE/rand/1/bin 有相似的收敛性；随着进化的进行，IDE 与DE/best/2/bin 有相似的收敛性。验证了式（2）和式（3）的有效结合，使得改进的DE 算法较好地平衡了算法前期的全局探索和后期的局部开发能力，不仅避免早熟收敛现象，同时加快了收敛速度。

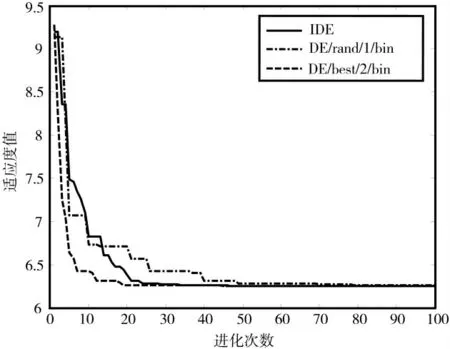
图2 改进型DE 和传统DE 适应度值进化曲线

图3～图5 给出了倒三角布站、星型布站和最优布站的定位精度GDOP 分布图。图中倒三角布站、星型布站和最优布站的位置坐标如表1 所示，图中以“*”表示。

由图3～图5 所示，经统计得到，GDOP 值小于10 m的定位精度覆盖率分别由倒三角布站和星型布站的23.4%、31.9%提高到采用最优布站的46.5%，系统的定位精度得到了显著的提高。

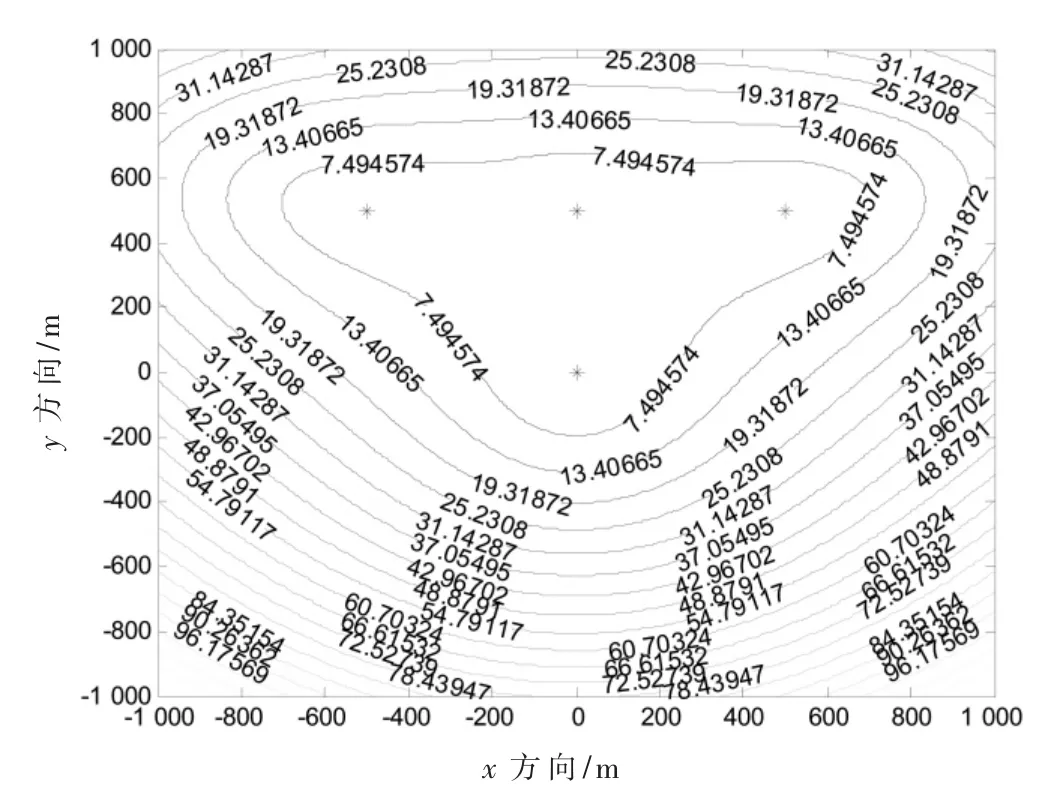
图3 倒三角布站GDOP 分布图

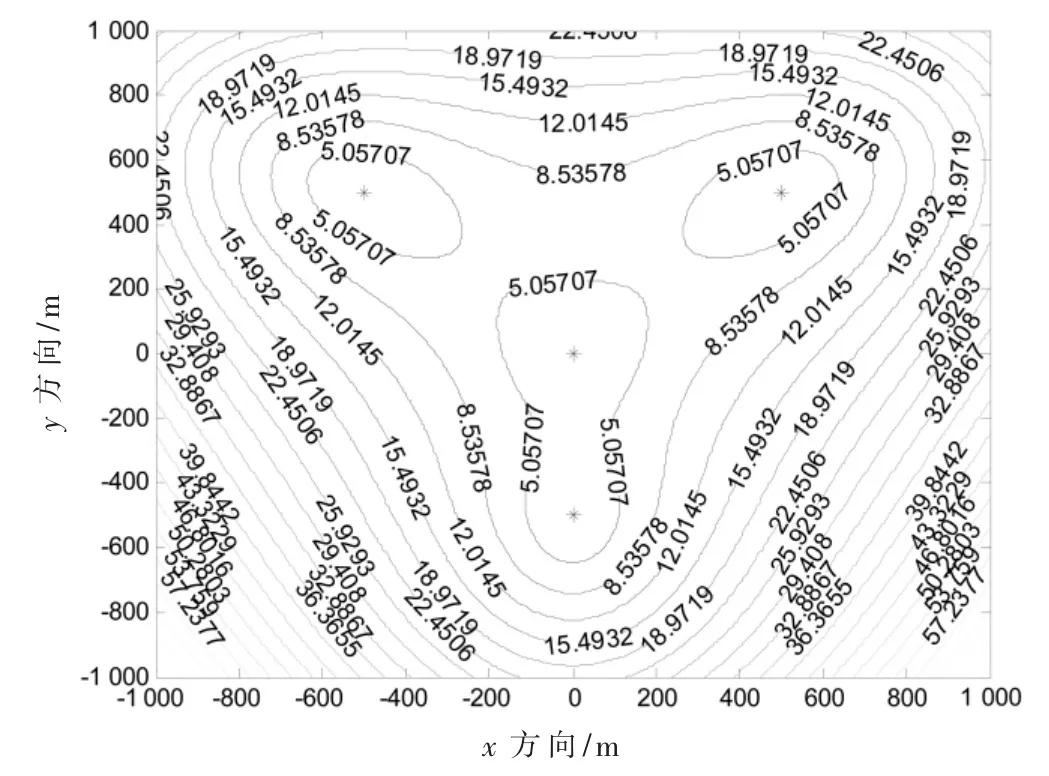
图4 星型布站GDOP 分布图

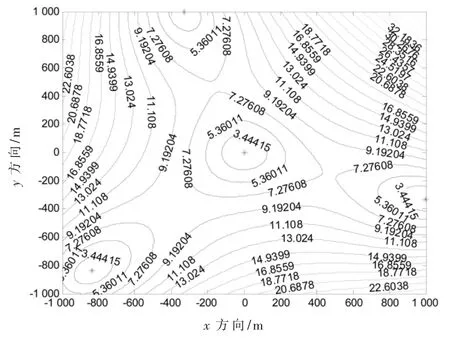
图5 最优布站方法GDOP 分布图

2.2 目标位置变化对系统定位精度的影响分析

仿真条件：设站点数量为4，其中1 个中心站，3 个基站，因此种群个体的维度D=10。倒三角布站、星型布站和最优布站的站点坐标如表1 所示。图6 给出了3 种布站方法的中心站上方定位精度GDOP 随目标高度变化的曲线图。

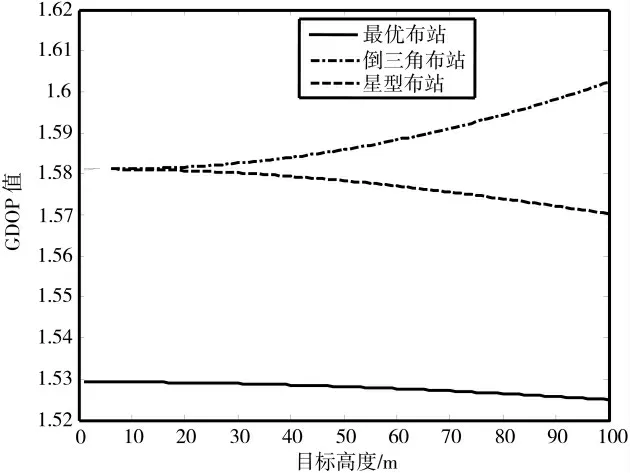
图6 定位精度GDOP 随目标高度变化曲线

由图6 可知，倒三角布站和星型布站中心站上方的定位精度GDOP 值变化趋势波动较大；最优布站的中心站上方的定位精度GDOP 值变化趋势波动较小，且定位精度较倒三角布站和星型布站得到显著的提高，验证了最优布站的定位精度对目标高度变化具有较好的鲁棒性。

图7 给出了3 种布站方法的定位精度GDOP 值随目标角度变化的曲线图。其中设目标高度为50 m，曲线值表征以中心站为中心，目标在半径500 m 圆周上移动时的GDOP 值。

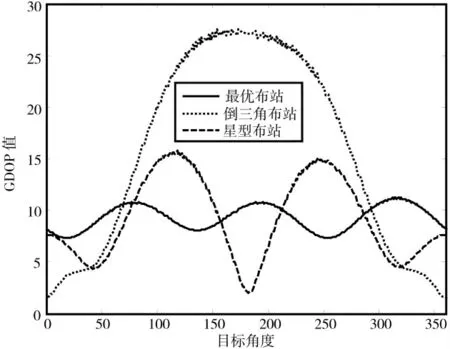
图7 定位精度GDOP 随目标角度变化曲线

由图7 可知，倒三角布站和星型布站中，目标角度发生变化，定位精度GDOP 值出现剧烈的波动，倒三角布站的定位精度波动最剧烈。相对于倒三角布站和星型布站，最优布站的定位精度GDOP 值随目标角度变化的波动较小，验证了最优布站的定位精度对目标角度变化表现出较好的鲁棒性。

3 结论

本文对差分进化算法进行了适当改进，较好地平衡了算法前期的全局探索和后期的局部开发能力，不仅能够避免早熟收敛现象，同时加快了收敛速度。算法以GDOP 为数据支撑，设计合理的适应度函数，结合多点定位系统的实际工程建设情况，建立仿真模型，通过不断地迭代产生最优布站的站点坐标。仿真结果验证了最优布站方法相比于传统布站，对目标的高度和角度变化表现出了较好的鲁棒性，布站区域内的定位精度得到了显著的提高，为系统实际工程建设提供可靠的理论依据。