基于DEM的民航地空VHF通信有效覆盖仿真研究

冯克涛, 李晓毅, 曲 晨, 王申涛, 陈 谋

(陆军工程大学通信士官学校, 重庆 400035)

0 引 言

甚高频(very high frequency, VHF)通信广泛运用于运输航空的地空通信,采用视距传播方式,由于其稳定性和可靠性高,是目前民航话音通信的主要方式,实现管制员与飞行员间的话音通信、指挥调度等功能,工作频率范围为117.975～137 MHz,由于发射频率高,表面波衰减较快,视距传播受地形、地物影响较大。对于塔台、终端(进近)等距离较近的VHF通信,可保证在管制范围内话音质量良好。而区域管制由于管制范围大、通信距离远,通信质量受飞机高度、障碍物等因素影响明显。随着民航飞行流量的逐年递增,管制部门对地空通信话音质量的要求越来越高。准确求解出VHF通信地面站在各个高度上的覆盖图,可以为VHF台站设备选址、航道规划等航空决策提供有力的图形和数据支持,具有重要意义。

计算VHF通信地面站覆盖区域时,传统方法为对选定地点进行障碍物高度测量,再按照民航相应规范使用简化计算公式,代入障碍物高度数据及目标覆盖高度,计算求出无线电理论覆盖距离。文献[2]和文献[5]中对影响VHF地空通信覆盖的主要因素进行了阐述。贾长东等描述了传统的遮蔽角计算和测绘;周宏宇等利用Matlab编程及GUI界面设计了VHF低空覆盖范围生成系统,直观、实用,但由于没有考虑地球曲率、大气折射、气象等因素影响,得到的覆盖范围比较粗略;康素成引入地理信息系统(geographic information system,GIS)空间分析技术建立了无线通信系统电波传播损耗模型,使用迭代法对无线通信系统电波传播损耗进行了参数校正;刘文评等使用Longley-Rice模型模拟信号衰减,得出“不规则地形是影响地面站覆盖的关键因素”结论;沈笑云等对气象多因素衰减进行了公式推导和计算,得到更贴近实际情况的覆盖效果。但是,上述文献中均缺乏对信号覆盖率的精确计算方法,忽略了遮蔽点具体点位的精准计算,缺乏实用性。

通视性问题分为点通视性、线通视性和区域通视性,本文中研究的民航地空VHF通信属于点对点的通视性问题。确定遮蔽点时,常用的求解方法为基于视线角(line of sight, LOS)通视分析的“最大斜率法”。“最大斜率法”在分析天线电磁波发射点与地形点之间的通视关系时,需要遍历计算每一个地形点,存在较大计算冗余;而在确定各方向最大斜率遮蔽角时,常常以离散分布的格网点直接作为遮蔽点进行计算,致使误差较大。

针对上述问题,为更好满足民航地空VHF通信应用需求,本文立足实际复杂地形,采用基于数字高程模型(digital elevation model,DEM)数据,对VHF通信地面站有效覆盖问题进行研究,对传统“最大斜率法”进行改进:采用“高程清洗”方法,减少了计算冗余;提出改进的反距离加权(inverse distance weighting,IDW)插值法对实验地形进行插值,提升DEM数据分辨率,提高了最大斜率遮蔽角计算精度;提出“切点截止法”精准求解遮蔽点位置坐标和盲区,并使用“网格法”准确计算覆盖率。仿真实验证明了本文所提的VHF通信地面站有效覆盖求解方法的有效性和实用性。

1 问题描述

1.1 起伏地形模型

DEM是地表形态的数字化表达,蕴含了丰富的地学应用分析所必需的地形地貌信息,坡度、坡向及坡度变化率等地貌特性均可在DEM的基础上派生。在GIS中,DEM有多种表示方法,主要包括等高线模型,规则网格(regular square grid,RSG)模型和不规则三角网(triangulated irregular network,TIN)模型3种基本模型。其中,规则网格模型数据具有结构简单、易于计算机处理、应用广泛等特点,考虑到算法的通用性,本文采用规则网络模型作为地理信息标准数据格式。

RSG地形模型可表示为

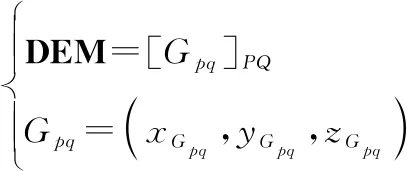
(1)

式中:表示第行与第列地形网格分割线的交点(即图1中网格交点),且∈[1,],∈[1,],、分别表示横、纵两维地形网格分割线数量的最大值。

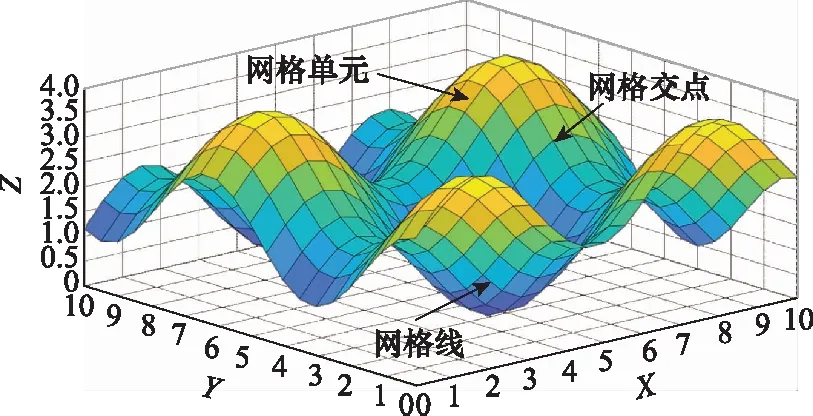
图1 RSG地形模型Fig.1 RSG terrain model

1.2 实验对象

本文以3个典型山地的DEM地形图作为研究对象,如图2所示。地形Ⅰ:天线高度为244.2 m,区域范围为40 km×40 km,分辨率为100 m,地形点数为401×401;地形Ⅱ:天线高度为203.3 m,区域范围为15 km×15 km, 分辨率为50 m,地形点数为301×301;地形Ⅲ:天线高度为55.5 m,区域范围为2 km×2 km, 分辨率为10 m,地形点数为201×201。

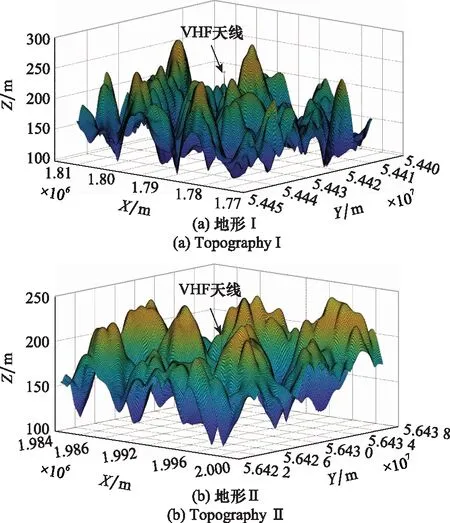
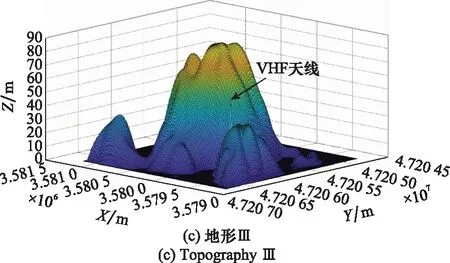
图2 仿真场景地形图Fig.2 Simulation scene topographic map

1.3 传统“最大斜率法”的局限性

一方面,地形高程数据的引入,使得计算遮蔽角的运算成本变得非常高。“最大斜率法”常用于电磁波的覆盖计算和仿真,而传统的算法对给定区域内的每一个网格节点均进行遮蔽角的计算,然后与基准遮蔽角进行对比,存在较大计算冗余。

另一方面,求解最大斜率遮蔽角受DEM分辨率影响存在一定误差。如图3所示,点为天线中心点,点为天线在地球面上的投影点,点为利用离散高程格网点求出的该方向最大斜率遮蔽点,线段为障碍物的切线,为切点。′和′分别为和延长线与高度平面的交点,和分别为点和点对应的遮蔽角。传统方法将tan近似为最大斜率进行计算,而实际上过点的线段才具有最大斜率tan。当DEM分辨率较低时,实际地形表示较概略,导致二者差值较大,直接制约计算精确度。科学提高DEM分辨率,有效确定切点的位置是精准确定遮蔽区的关键。

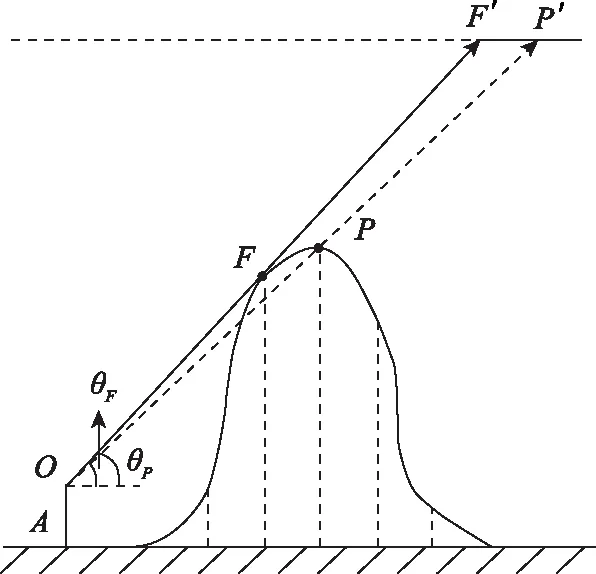
图3 最大斜率示意图Fig.3 Maximum slope diagram

2 改进的自适应粒子群算法优化反距离加权插值法

2.1 IDW插值法

IDW插值法具有原理简单、计算简便、遵循地理学第一定律的特点,在GIS软件开发、降水数据分析、PM 2.5异质性研究和土壤成分变异研究等方面具有广泛应用。计算模型为

(2)

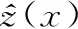
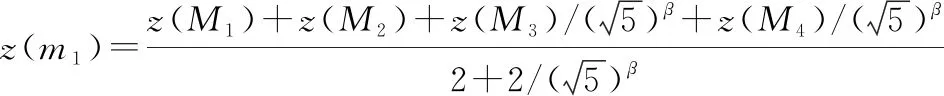
(3)

(4)

()=[()+()+()+()]4

(5)

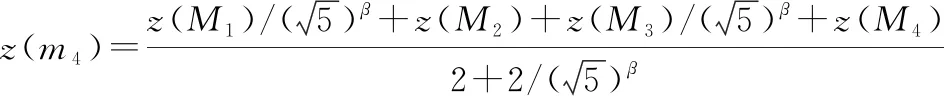
(6)

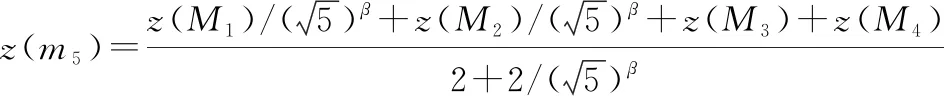
(7)

图4 IDW插值示意图Fig.4 IDW interpolation diagram

2.2 改进的自适应粒子群算法

粒子群算法是由Kennedy和Eberhart提出的一种群体智能算法,通过搜索个体和种群全局的最优位置,进而能以较大的概率收敛于全局最优解。而其参数取值是影响算法性能和效率的关键,若参数设计选择不恰当,容易引起种群“早熟”,丧失多样性,导致算法不能收敛到全局最优解。本文在文献[25]的基础上,对惯性权重进行非线性自适应改进,使其能紧跟种群全局优化的方向而随之变化,提高搜索值精度。

设在一个维空间中,由个粒子组成种群=(,,…,),其中第个粒子位置为=(1,2,…,),其速度为=(1,2,…,),经过的最佳位置为=(1,2,…,),种群全局最佳位置为=(1,2,…,)。设()为适应度函数,则粒子依据当前适应度值的变化对和进行更新,方程为

(9)

式中:表示当前迭代次数;=1,2,…,;是第个粒子的第维分量,且有=1,2,…,。按照追随当前最优粒子的原理,粒子的进化方程为

(+1)=()+1()[()-()]+

2()[()-()]

(10)

(+1)=()+(+1)

(11)

式中:1、2为[0,1]之间的随机数;为惯性权重;为自我学习因子,为社会学习因子。

本文以粒子当前距全局最优位置的距离对进行非线性设计,公式为

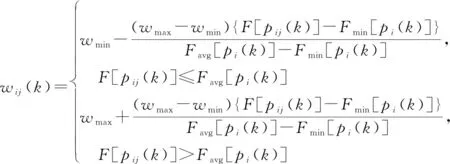
(12)

式中:、分别为初始最大惯性权重和最小惯性权重;[()]表示粒子当前的适应度值,[()]、[()]分别表示当前所有粒子适应度的平均值和最小值。

分析可知,当粒子适应度分散时,()减小,反之则增加,使得惯性权重在[,]区间基础上适当展宽,更有利于全局搜索和局部搜索功能的动态转换。本文取=095,=04,大量实验证明当取上述值时算法性能会有明显提升。

学习因子和分别按式(13)和式(14)进行自适应变化:

=1max-(1max-1min)

(13)

=2min+(2max-2min)

(14)

式中:1max和1min分别是的最大值和最小值;2max和2min分别是的最大值和最小值;为最大迭代次数。本文取1max=2max=205,1min=2min=195。

2.3 插值效果评价

为检验插值方法的有效性,使用平均绝对误差(mean absolute error, MAE)、均方根预测误差(root mean square prediction error, RMSPE)和相关系数对插值效果进行统计分析。各统计量的表达式为

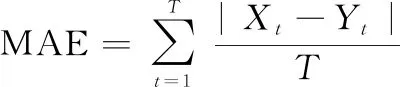
(15)

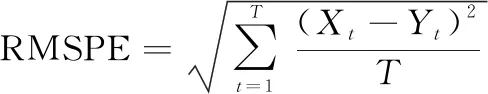
(16)

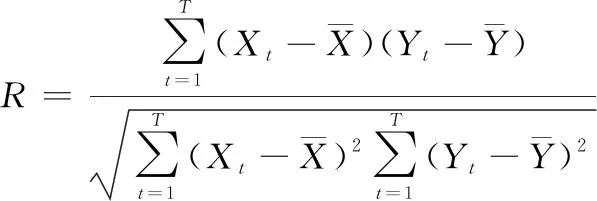
(17)

2.4 改进的自适应粒子群算法优化搜索幂指数β最佳值

应用IDW插值法时面临的主要困难是设置幂指数值,搜索最佳值的传统方法是穷举搜索,但该方法只能保证找到局部最优解。文献[28]和文献[29]分别采用粒子群算法和遗传算法进行了有益探索,提高了搜索近似最优解效率。本文采用改进的粒子群算法对幂指数最佳值进行搜索,给定粒子运动位置区间=[min,max]和速度区间=[-,],算法就会在限定范围内进行全局搜索,找到粒子的最优位置。本文以样本点值与插值的残差绝对值和最小值作为适应度函数,即

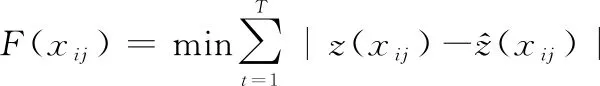
(18)

约束条件为

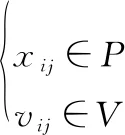
(19)

2.5 算法收敛精度分析

为检验本文算法收敛精度的优势,设计了仿真。仿真环境为搭载Intel Core i7 2.8 GHz处理器,内存24 GB的MECHREVO(X6Ti-S),操作系统为Windows 10专业版64位,使用Matlab 2019b作为仿真平台。实验与文献[25,28]中提出的粒子群算法进行优化对比,所选取的两种对比算法的、和等参数均按照原文献进行设置。粒子种群规模统一设置=50,最大迭代次数=100,粒子最大速度=01,每种地形各方法分别运行30次取最佳值,仿真结果如表1所示。

表1 IDW插值效果对比

续表1

分析可知,文献[28]方法耗时最短,本文算法耗时最长,分别延时增加22.9%、9.3%和10.5%;MAE对比本文最小,相对次佳方法分别降低2.3×10、0和3.3×10;RMSPE对比本文最小,分别相对次佳方法降低2.3×10、0和1.3×10。本文方法MAE和RMSPE值均为最小,说明插值后的DEM结果相对于真实数据的差距最小,本文方法求解的值最好。图5描述了在3个地形中MAE与幂指数之间的关系,3条曲线都存在极小值,精准确定幂指数是使用IDW插值法的关键。

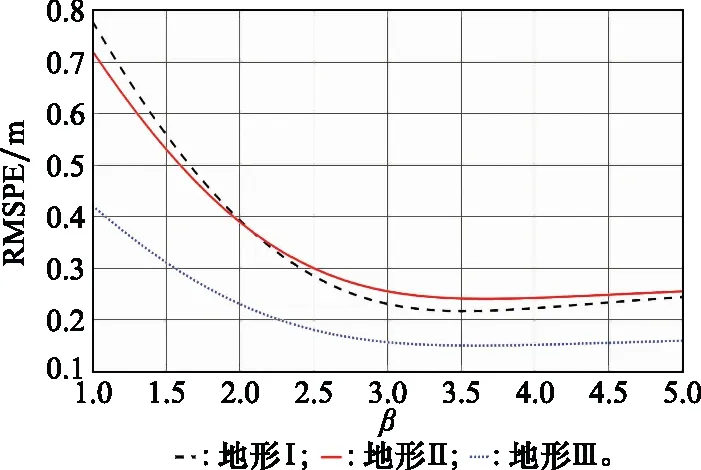
图5 RMSPE变化情况Fig.5 Change of RMSPE

3 改进的“最大斜率法”

3.1 “高程清洗”

本文基于“设定基准高程面重点计算”的思想,采用“高程清洗”的方法,对传统“最大斜率法”进行改进,不需要计算区域内每一个地物点的斜率(遮蔽角),可有效减少计算冗余,提高计算效率。

设VHF电台天线坐标为=(,,),周围地形矩阵为=(,,),定义bj(,)为标记函数,其中

(20)

得到标记矩阵=(,,bj(,))。显然,bj(,)=0的地物点不会对电台天线造成遮蔽,不需要对其进行斜率计算。若bj(,)中0和1的数量分别为和,则相对传统最大斜率法减少的计算量比例为

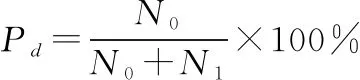
(21)

3.2 采用DEM插值方法提高地形辨识度

DEM数据承载了地貌形态、地表起伏、地势走向等重要信息,但是难以获取区域内连续的空间信息,造成真实地形局部信息缺失,一定程度上影响后续的地形分析。而实用的有效方法是依托现有的地形数据信息,通过合适的插值方法利用实测点信息估计未测点信息,提升地图分辨率,进而提高地形的辨识度。本质上,许多空间插值方法都是通过相邻样本点测量值的加权平均值预测得到特定位置的高程值,估计公式通常为

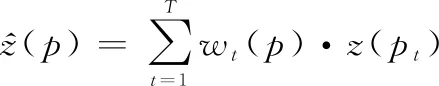
(22)

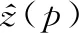
3.3 方法步骤

导入DEM数据。

对DEM数据进行插值,提高分辨率。选用改进的IDW插值法(值取表1中本文方法求得的对应值)、双线性插值(bilinear interpolation,BI)法和普通克里金(ordinary Kriging,OK)插值法对3种不同分辨率的DEM实验地形数据进行插值对比分析,并挑选出最佳方案。插值效果如表2～表4所示。

表2 地形Ⅰ插值效果对比

表3 地形Ⅱ插值效果对比

表4 地形Ⅲ插值效果对比

分析可知,BI算法耗时最短,IDW算法次之,OK算法耗时最长,相对BI算法IDW算法分别延时增加354.7%、181.6%和186.9%;MAE对比IDW算法最小,分别相对次佳算法降低42.3%、35.9%和36.5%;RMSPE对比IDW算法最小,分别相对次佳算法降低20.1%、12.0%和11.9%。在3个实验地形中,IDW算法虽然耗时介于BI法和OK法之间不是最佳,但是MAE和RMSPE值均为最小,且相关系数最大,说明插值后的DEM结果相对于真实数据的差距最小,更加符合真实地形地貌特征。故综合比较后选用IDW算法进行插值,DEM分辨率依次变化为50 m、25 m和5 m。

“高程清洗”。以天线高度为基准作参考面,按式(20)对插值后的地形图进行标记处理。

高差改正。地球曲率和大气折光差在许多小数据量(小范围)的可视计算中常被忽略,但在大范围的计算中,是一个非常重要的影响因素,必须加以考虑,且计算半径越大,影响越显著,进而影响遮蔽角的计算准确度。为抵消大气折射的影响,通常使用等效地球半径代替实际地球半径,把大气折射作用形成的电磁波传播轨迹等效为直线,使视距传播距离的分析和计算得以简化。可用地球曲率补偿公式对高程进行高差改正:

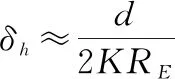
(23)

式中:为高差改正系数,反映由地球曲率引起的高程变化;为地物点与天线中心点之间的水平距离;为大气折光差系数,通常在标准大气压下取值133;为地球半径:

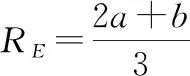
(24)

式中:为地球椭球体长半轴(6 378.2 km),为地球椭球体短半轴(6 356.8 km)。

若为地物点的海拔高度值,则高差改正后的高程为

=-

(25)

确定切点逼近点。首先以VHF天线中心点为圆心,寻找各方向上的最大斜率遮蔽点集合={,,…,}。在图6中,为集合中的任一点,～为距距离最近的8个网格节点,按式(2)再次进行IDW插值法计算得到～,进一步提升局部的地形分辨率。最后依次计算～和相对于点的斜率tan，tan，…，tan和tan,取最大值tan作为该方向的最大斜率进行计算,并把该点确定为该方向的切点逼近点。

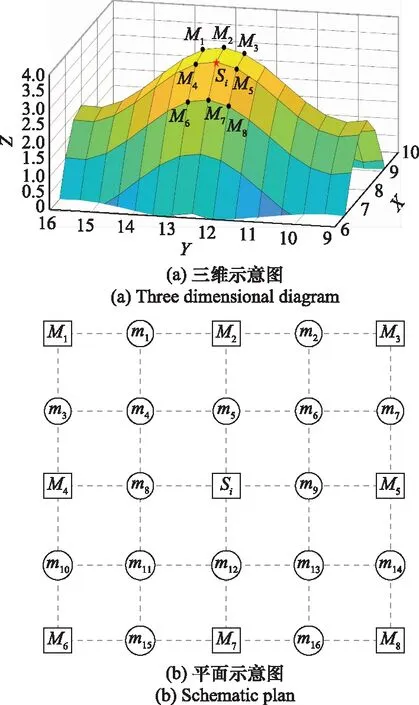
图6 IDW插值法确定切点逼近点Fig.6 Determination of tangent point approximation point by IDW interpolation method

绕射影响。电磁波在遮蔽物附近传播时会产生绕射现象。因此,计算遮蔽角时需增加一个角度修正量Δ:

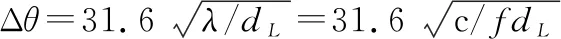
(26)

式中:c为光速;为电台工作波长;为电台工作频率;为天线中心点与切点之间的斜距离(即图3中的线段)。在实际应用中加入修正因子修正后的最大斜率遮蔽角计算公式为

=+Δ

(27)

4 基于改进的“最大斜率法”分析VHF信号覆盖

计算VHF地面通信站覆盖范围要重点综合考虑最远有效通信距离、各方向最大斜率遮蔽角、地球曲率半径、大气折射、飞行高度等因素。需要注意以下3个问题:

(1) 数字地图精度适当符合要求,需准确反映地形的地貌信息;

(2) 地面站信号覆盖需综合考虑视距传播截止距离、自由空间电磁波传输距离和满足电磁波场强要求的距离,三者最小值确定为最远有效通信距离;

(3) 利用切点逼近点计算各方向的最大斜率遮蔽角,提高精度;

VHF地面通信站信号覆盖计算流程如图7所示,具体步骤如下。

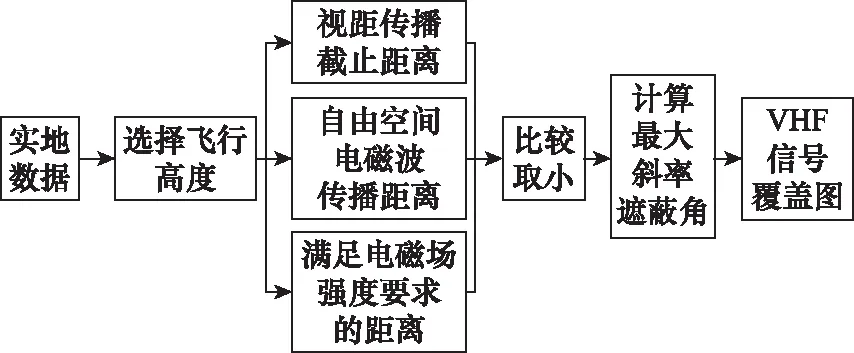
图7 VHF地面通信站信号覆盖计算流程Fig.7 Signal coverage calculation flow of VHF ground communication station

DEM数据导入及数据处理。按照第3.3节步骤2～步骤4对导入的DEM数据进行插值、“高程清洗”和高差改正。

选择飞行高度层。《航空无线电导航台和交通管制雷达站设置场地规范》规定,需要画出4 500 m、7 000 m、10 000 m高度的360°方位覆盖情况,为选择飞行高度提供依据。

确定最远有效通信距离。

(1) 基于视距传播的最远距离

VHF电波为直视传播,发射机与接收机之间的电波传播路径是一条直线。由于地球凸起的球面影响,会对传播路径进行阻挡。考虑大气折射,电磁波的传播路径通常弯向地球方向,使VHF视距得到延伸。假设折射率变换率随高度保持不变,利用等效地球半径=(43)(为地球半径)可得到电磁波等效直线传播模型,如图8所示。

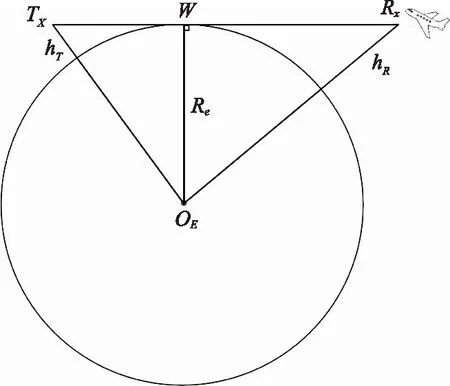
图8 地球曲率对VHF信号的遮挡Fig.8 Occlusion of VHF signal by earth curvature

图8中,为地球球心,为地面发射站与飞机接收设备连线与球面相切的切点,则传输距离近似表达式为

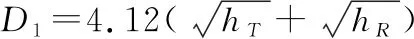
(28)

式中:、分别表示地面发射站和飞机接收设备的天线高度,单位为m;单位为km。

(2) 基于自由空间电磁波传输的最远距离

VHF通信以电磁波形式在大气中传输时会引起能量损耗,采用直视通路在自由空间传播,传输损耗为

=3244+20lg+20lg

(29)

式中:为传输损耗, 单位为dBm;为电台频率, 单位为MHz;为最远通信距离, 单位为km。在实际传输过程中,传播介质(大气气体)也会带来衰减,需考虑传播媒介衰减因子(在地空通信中通常取=09)。最远通信距离为

20lg=-+20lg-3244-20lg

(30)

式中:为发射功率, 单位为dBm;为接收机灵敏度, 单位为dBm。

(3) 基于VHF设备电磁波场强要求的最远距离

根据《国际民用航空公约》附件10《航空通信》中的技术规范要求:地面VHF设备接收电磁场强度≥20 μV/m,机载VHF接收设备电磁场强度≥75 μV/m。根据文献[2]推导得到在自由空间距离天线距离处的场强为

(31)

式中:为发射机天线增益。当取最小信号场强时,得到最远通信距离:

(32)

综上,最远有效通信距离取3个距离中的最小值,即

=min{,,}

(33)

确定遮蔽区域。

计算基准遮蔽角。

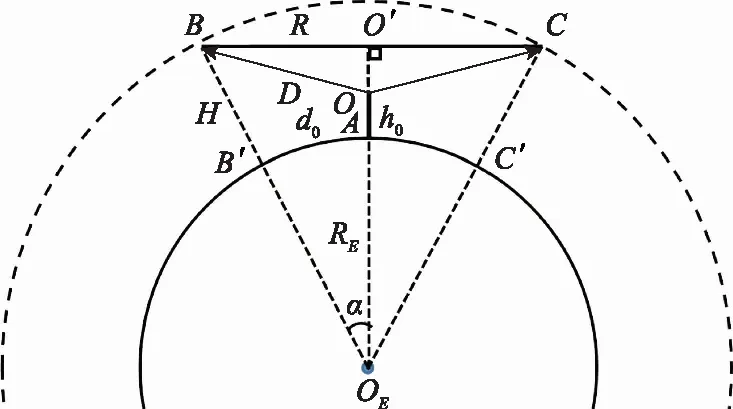
图9 覆盖范围示意图Fig.9 Schematic diagram of coverage

根据余弦定理,有

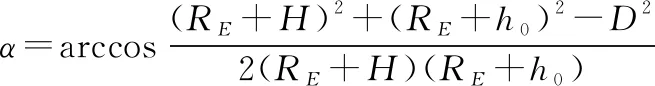
(34)

则天线在高度条件下求解的通信覆盖范围半径为

=(+)sin

(35)

与之间的水平距离为

=·

(36)

如图10所示,′为高度经过式(25)高差改正后的高程,为基准遮蔽角,则有

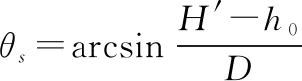
(37)

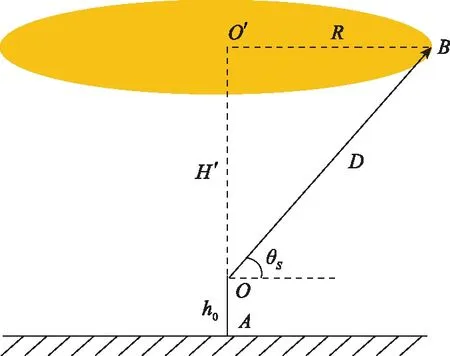
图10 基准遮蔽角示意图Fig.10 Schematic diagram of reference shielding angle

确定各个方向的最大斜率遮蔽角。

按照第33节步骤5和步骤6计算得到各个方向的切点逼近点集合={,,…,}和对应的最大斜率遮蔽角集合={,,…,}。

确定切点逼近点在飞行高度的投影点位置。

图11中,各点的高程已进行高差改正,(,,)为天线中心位置,(,,)为切点逼近点,(,,′)为因切点逼近点阻挡在′高度平面的投影点,′、′分别为、在天线高度平面的投影点,Δ为绕射引起的角度修正量,为修正后的最大斜率遮蔽角,为′与轴的夹角。

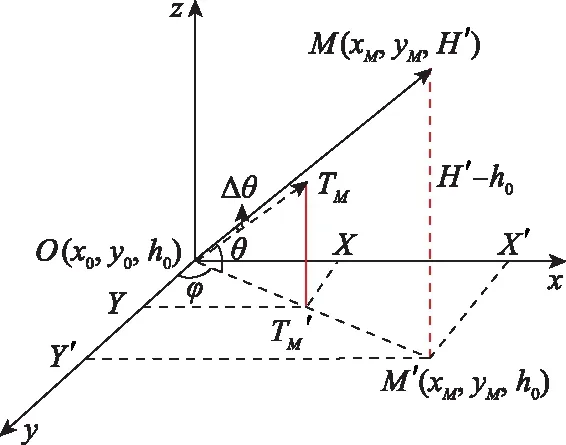
图11 遮蔽点投影点位置示意图Fig.11 Schematic diagram of shadow point projection point position

由图示关系可知:

′=(′-)cot

(38)

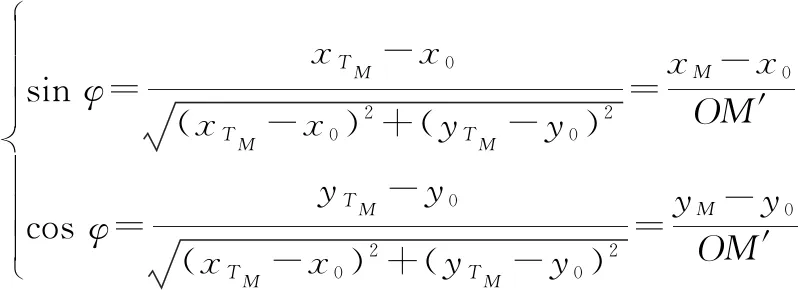
(39)

联立解得

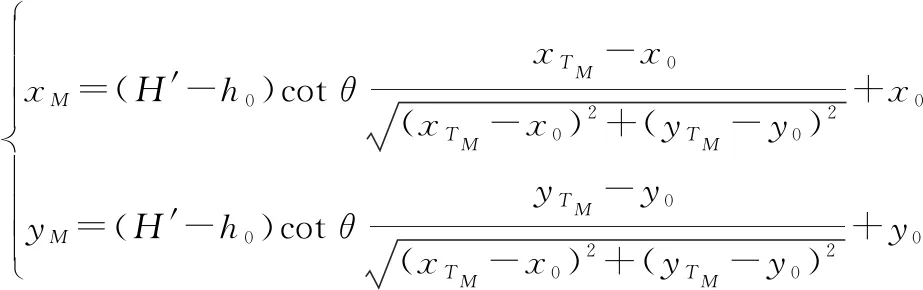
(40)

计算遮蔽区域坐标值。

如图12所示,当≥时,采用“切点截止法”分析:由于切点为遮蔽点,根据电磁波的直线传播原理可知,电磁波在点传播截止,无法向点延伸,故即为点导致的遮蔽区。

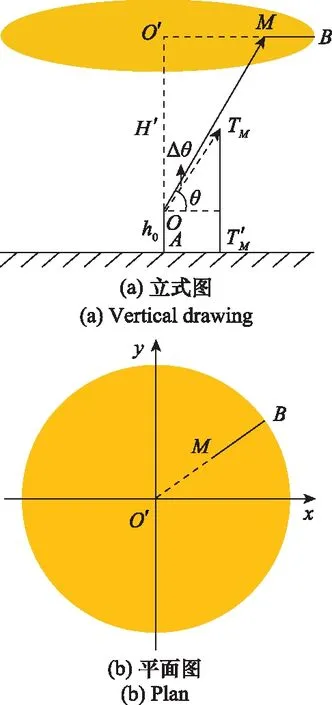
图12 遮蔽区域示意图Fig.12 Schematic diagram of sheltered area

利用′、、三点在同一直线上,且圆半径′=,可求出线段的表达式为

(41)

设点的坐标为(,,′),则有

(42)

展开可得

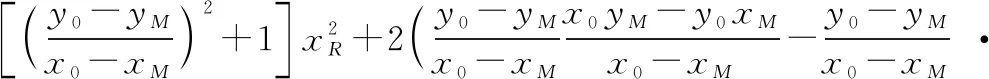
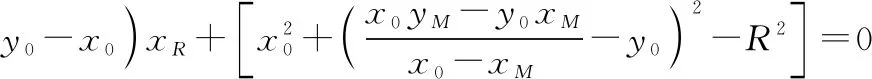
(43)

令

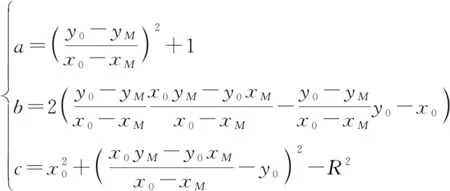
解得为

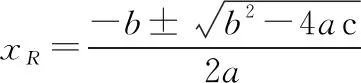
(44)

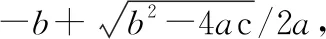
绘制覆盖图,并用“网格法”计算天线通信覆盖率。

先依据圆心、最远有效距离作半径画出包络覆盖切面圆,并进行网格分割(见图13(a));

然后将覆盖面圆中的每个网格置为“1”,并用白色“”作图(为便于观察,图13(b)中用“〇”表示);

再将所有遮蔽点所在的网格置为“0”,并用黑色“”替代白色“”作图(为便于观察,图13(c)中用“·”表示);

最后统计步骤52和步骤53中“1”的数量分别为和,则信号覆盖率为

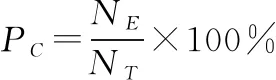
(45)

最后的仿真结果示例如图14所示。

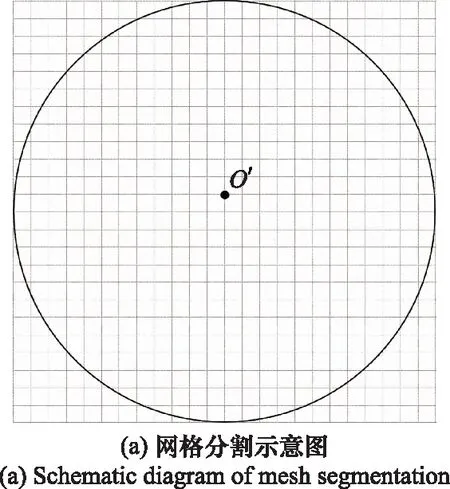
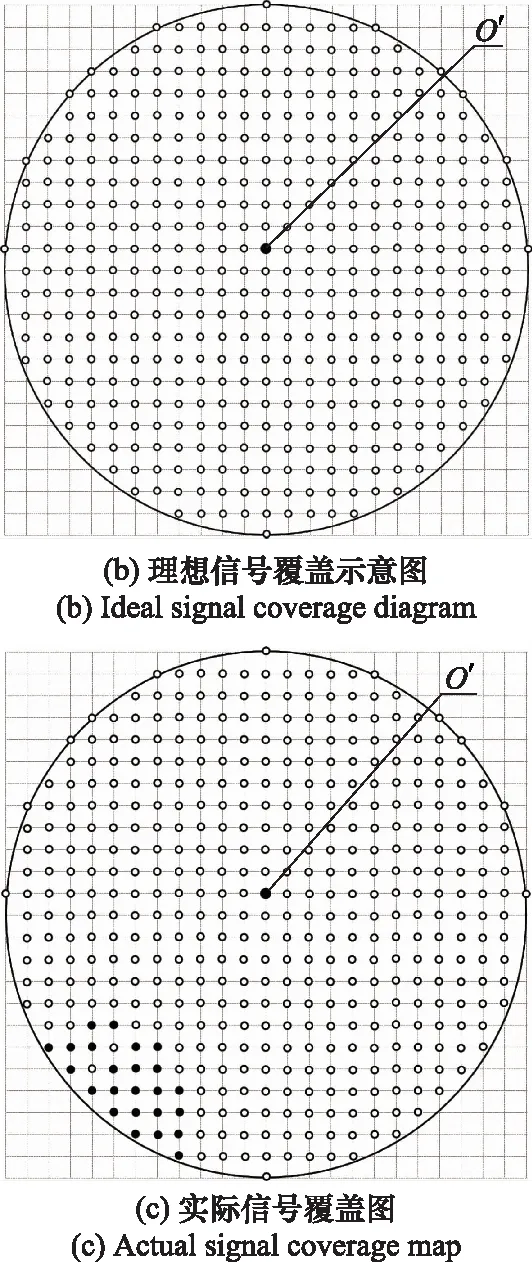
图13 信号覆盖示例图Fig.13 Example of signal coverage

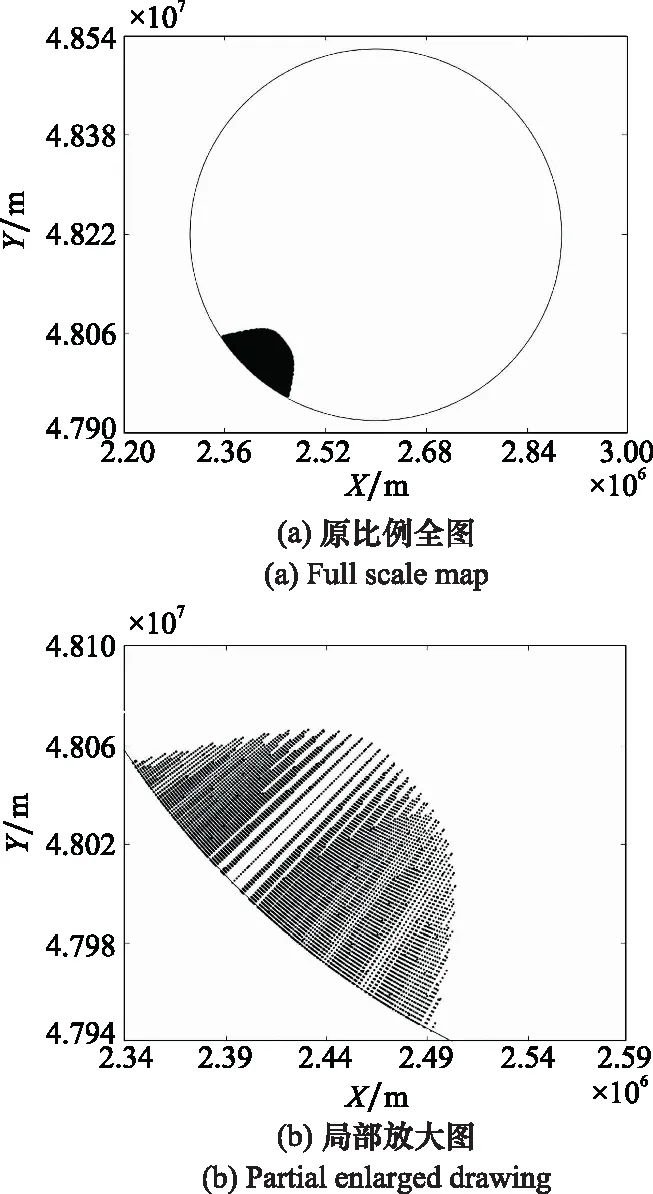
图14 信号仿真覆盖示例图Fig.14 Example of signal simulation coverage

5 算法验证

5.1 改进“最大斜率法”算法验证

为验证改进“最大斜率法”的有效性与先进性,计算分析3个典型地形在4 500 m高度上各自天线信号被遮蔽的仿真情况,并与传统算法运算耗时和覆盖率进行对比分析,改进方法与传统方法的信号覆盖对比见图15。仿真条件如表5所示,运行结果如表6、表7所示。

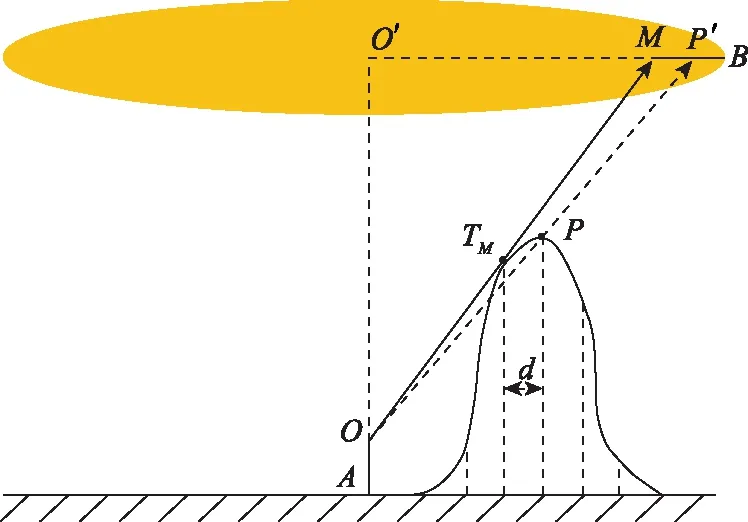
图15 信号覆盖对比图Fig.15 Signal coverage comparison chart

表5 仿真条件

表6 遮蔽角计算耗时比较

表7 覆盖率计算比较

图15中,设定实验地形的DEM原始分辨率为2,则经过一次IDW插值后的分辨率提升为,为原始分辨率下求得的最大斜率遮蔽点,为分辨率提升后求得的切点逼近点,′和分别为和延长线与设定高度平面的交点。

表6为传统最大斜率算法和本文方法对各原始地形未插值前计算遮蔽角的耗时对比,时间为经40次实验后的平均耗时结果。由表6可知,相较于传统方法,本文所提“高程清洗”的改进方法可分别节省时间68.1%、54.5%、69.2%。

表7为在不同地形条件下VHF地面通信站在4 500 m高度的通信覆盖率结果,相较于插值前的传统算法,插值后的覆盖率分别降低9.58%、4.10%和1.26‰。结合图15和表7分析可知,实验地形经插值后分辨率提升,提取到的地形数据与实际地形更加接近,其中引起VHF信号遮蔽的局部地物点被恢复,求得的切点逼近点相较于点更加接近真实切点位置,同时投影点相较于点′更接近圆心′。由于遮蔽区域>′,因此本文方法比传统方法计算得到的覆盖率低。同时,随着原始DEM数据分辨率的逐步提升,地形地貌信息更加完善,不仅恢复出的点与点的重合几率增大,而且未重合的点与点导致的遮蔽投影点位置更加逼近,导致后续计算的覆盖率下降幅度随之减小。

5.2 改进的VHF有效覆盖范围仿真程序

针对文献[7]设计的“VHF低空覆盖范围生成系统”欠缺地球曲率和大气折射影响、覆盖盲区边缘轮廓显示粗略的局限,本文利用改进的最大斜率法依托Matlab平台编写设计了VHF有效覆盖范围仿真程序,并选取地形Ⅲ为例进行仿真对比。

实验参数设置:飞行高度分别为4 500 m、7 000 m和10 000 m时,导入起伏地形的DEM数据,在程序里输入天线高度、飞行高度、VHF频率、发射功率、天线增益、最低信号场强、接收机灵敏度等参数(实验条件同表5)即可生成VHF有效覆盖范围图(见图16)。

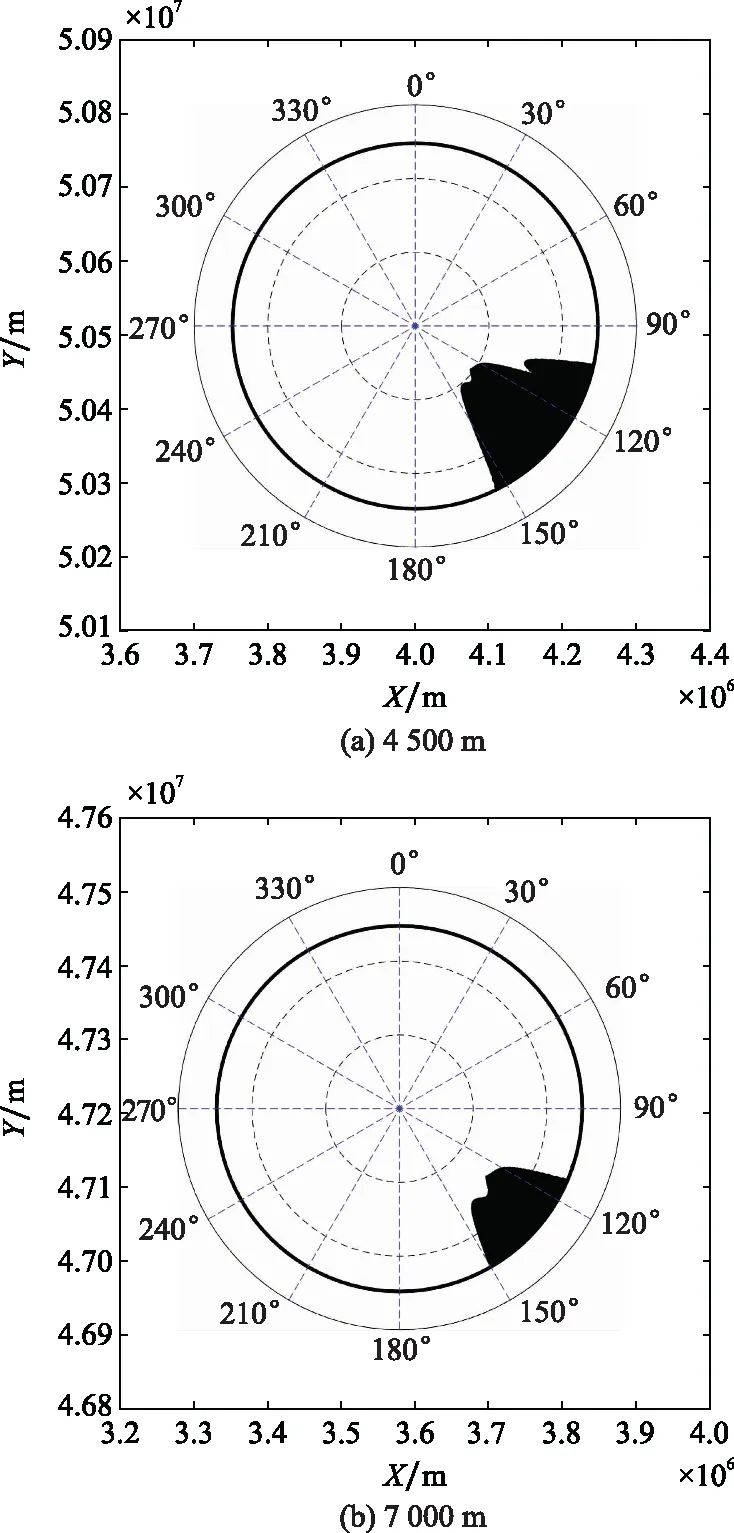
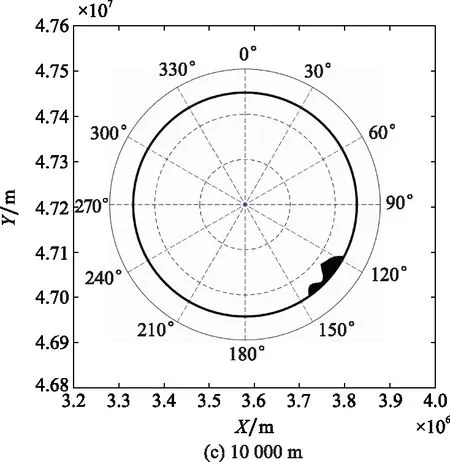
图16 各飞行高度的通信覆盖图Fig.16 Communication coverage map of each flight altitude

图16中,0°表示VHF地面站磁北方向;从外向内依次为300 km刻度线(细实线)、VHF理论覆盖范围(粗实线)、200 km刻度线(虚线)和100 km刻度线(虚线);粗线圆中的白色区域为信号有效覆盖区域,黑色阴影部分为遮蔽物引起的覆盖盲区。相关仿真结果如表8所示。

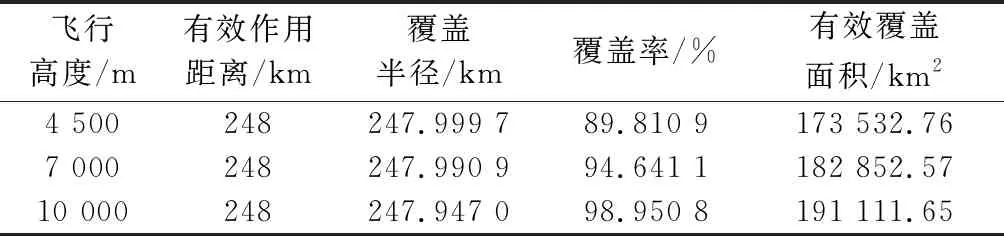
表8 仿真结果

同时,可利用程序将覆盖情况生成0-1矩阵(“1”表示有效覆盖区域,“0”表示覆盖盲区),导出为EXCEL表格,将“1”替代为空格后,各飞行高度的通信覆盖情况如图17所示。

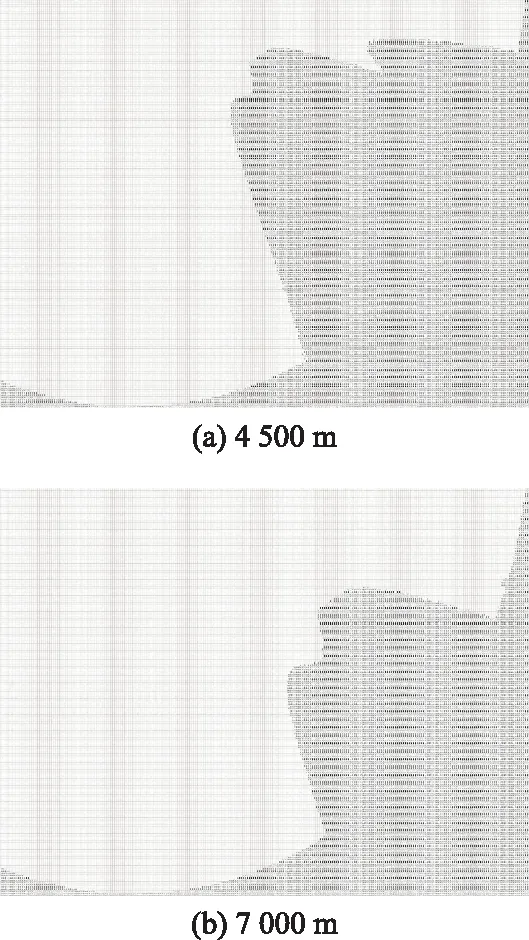
图17 使用表格数据显示的各飞行高度的通信覆盖情况Fig.17 Communication coverage of each flight altitude displayed by table data

结合图16、图17和表8可知,随着飞行高度增加,覆盖半径有细微的减小趋势,阴影部分变小,覆盖率增大。与文献[7]相比,首先,本文设计的VHF有效覆盖范围仿真程序考虑了地球曲率、大气折射和传播媒介衰减等影响,最远有效通信距离计算更准确;其次,最远盲区轮廓更平滑贴近实际;最后,可从程序中读出任意一点的、坐标,可为VHF地面通信站选址、飞机航线规划提供更准确的数据支撑。

6 结 论

重点研究了实际起伏环境下民航VHF地空通信有效覆盖问题,提出了改进的“最大斜率法”。考虑遮蔽点精准定位,提出“切点截止法”,并使用“网格法”计算信号有效覆盖率。实验结果表明,采用“高程清洗”方法能够降低计算冗余;使用改进的IDW插值法可有效提升实验地形分辨率,进而提高最大斜率遮蔽角的计算精度。设计了仿真程序,可根据备选站点周边实地数据仿真得到其VHF有效覆盖范围,从而为民航VHF地面通信站选址决策、航线规划提供科学依据,具有一定的应用价值。为获得更准确的有效覆盖范围,下一步还需要从电磁干扰方面进行分析。