滑动式Lagrange与Chebyshev插值方法对BDS精密星历内插及其精度分析

梁 珂，周晓敏，隋立春，刘伟东

（1.自然资源部第一大地测量队，西安 710054；2.长安大学 地质工程与测绘学院，西安 710054）

0 引言

2020年6月23日，北斗卫星导航系统（BeiDou navigation satellite system，BDS）正式完成组网，成为全球卫星导航系统（global navigation satellite system, GNSS）家族中的一员。与全球定位系统（global positioning system，GPS）相比，BDS导航卫星星座由混合星座组成，包括地球静止轨道（geostationary Earth orbit, GEO）卫星、倾斜地球同步轨道（inclined geosynchronous orbits, IGSO）卫星、中圆地球轨道（medium Earth orbit, MEO）卫星[1-3]。BDS在定位过程中，需要分析中心提供精密星历获取卫星三维坐标信息[4]。一般提供的精密星历产品文件时间间隔为 15 min，但是接收机的采样间隔时间一般为30、10 或1 s，因此，BDS在定位过程需要获取任意时刻卫星三维坐标信息。获取任意历元 BDS卫星三维位置成为 BDS定位过程中需解决的问题之一[5]。国内外学者研究表明：插值法是获取任意历元BDS卫星三维位置最简单、高效的方法之一[6]。目前对 BDS精密星历插值的数学方法主要包括：埃尔米特（Hermite）插值、三角函数插值、拉格朗日（Lagrange）插值、牛顿（Newton）插值、切比雪夫（Chebyshev）插值、三次样条插值等。文献[7]对比分析了滑动式与非滑动式Lagrange插值方法对BDS精密星历进行内插结果的影响，其结果表明，滑动式 Lagrange插值效果明显优于非滑动式 Lagrange插值效果，滑动式Lagrange插值对GEO、IGSO、MEO卫星插值都能达到毫米级精度；文献[8] 对比滑动式傅里叶级数插值与9阶Chebyshev插值对比分析，其结果表明，9阶Chebyshev插值更适用于GEO卫星与IGSO卫星，而MEO卫星使用傅里叶级数插值精度更高；文献[9] 采用 Lagrange插值与Chebyshev插值对精密星历进行内插对比分析，结果表明：采用一定的阶数精密星历内插均可以达到毫米级精度，且二者插值效果接近。本文基于滑动式 Lagrange插值和 Chebyshev插值方法，分别对BDS三种不同卫星精密星历内插，对比分析二者插值方法的特点和精度，旨在为今后BDS定位过程中获取任意历元卫星三维坐标信息提供参考。

1 插值数学模型

1.1 Lagrange插值数学模型

Lagrange插值法为：假设y=f(xi)在区间[a,b]上是个实函数，且在区间[a,b]上n+1阶可导，那么在区间[a,b]上任意一点x的n阶Lagrange插值多项式代数表达式为

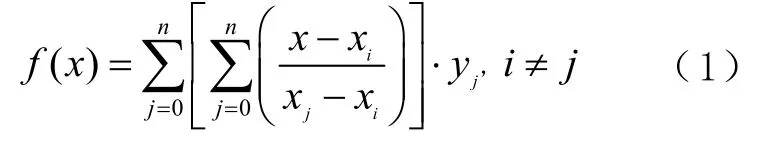
式中：f(x)为插值节点处函数值；n为插值多项式的阶数；为插值基函数，仅与插值节点有关。

对BDS精密星历进行n阶Lagrange内插，在插值时选择一个区间[t0,t1]，即可求出任意时刻卫星在X、Y和Z方向上的坐标分量，从而得到任意历元卫星的位置。任意历元卫星位置表示为

式中：i≠ j，（Xt、Yt、Zt）为t时刻卫星位置三维坐标分量；ti、tj为插值区间任意常数。

Lagrange插值方法在插值两端易产生“龙格”现象，为进一步提高BDS精密星历内插的精度，使用滑动式Lagrange插值方法获取任意历元卫星三维坐标分量，可以有效避免“龙格”现象的产生[7-8]。

滑动式Lagrange插值方法为：在进行Lagrange插值时，不断改变插值区间，使待插值点一直保持在插值区间的中间点上，以此来提高插值的精度。滑动式 Lagrange插值可以抑制插值区间两端插值结果的震荡[9-10]，使插值结果精度达到最优。对BDS精密星历进行n阶Lagrange内插，当n为偶数时，生成n-1（奇数）阶插值多项式，若选择12个插值节点，可以生成11阶插值多项式，此时求得的插值结果只保留第 4个和第 5个插值节点中间的插值结果；当n为奇数时，生成n-1（偶数）阶插值多项式，若选择 13个插值节点，可以生成12阶插值多项式，此时求得的插值结果只保留第5个和第6个、第6个和第7个插值节点中间的插值结果，将其他节点插值结果舍去。

1.2 Chebyshev插值数学模型

Chebyshev多项式拟合是采用函数最佳逼近的原理，根据已知节点生成一个函数，使其在给定点的函数值与该点函数值之间的方差和最小，且该函数是以Chebyshev多项式为基函数构成的。如果在区间[t0,t0+Δt]内的卫星星历使用Chebyshev多项式进行拟合，同时将卫星轨道进行标准化处理，对时间进行转换，将其定义为

式中：t∈[−1 ,1]，t0和∆t分别为开始历元与拟合区间的长度；t为区间[t0,t0 +Δt]中任意常数，此时卫星三维坐标分量（Xt、Yt、Zt）可表示为

式中：aXi、aYi、aZi分别为相应分量的Chebyshev多项式的系数；Ti(τt) 为Chebyshev多项式。

2 算例分析

为对比分析不同阶数滑动式 Lagrange插值与Chebyshev插值方法对 BDS精密星历的精度，本文借助武汉大学国际 GNSS服务（International GNSS Service, IGS）数据中心提供的BDS精密星历产品，采用滑动式 Lagrange插值与 Chebyshev插值方法分别对 GEO卫星、IGSO卫星、MEO卫星精密星历进行内插，实验流程如图1所示。图1中：RMS（root mean square error）为均方根误差。

图1 实验流程

本次实验数据起始历元为2020-01-01 T 00:00:00，终止历元为2020-01-02 T 23:30:00，为Lagrange插值方法和Chebyshev插值方法的区间长度，以BDS精密星历产品中，每30 min间隔的卫星三维坐标作为已知点，以每15 min间隔的卫星三维坐标作为参考值，将计算得到的内插值与参考值进行求差得到残差，以残差的均方差根结果表示插值的精度因子。本次实验观测中任选 PC02（GEO卫星）、PC08（IGSO卫星）、PC12（MEO卫星）三颗卫星分别进行5阶至20阶滑动式Lagrange插值和Chebyshev插值，对其结果进行统计分析，其结果如表1至表3所示，为了更加直观反映出插值结果，将插值结果可视化输出，结果如图2至图7所示。

图2 不同阶数滑动式Lagrange插值方法对GEO卫星的影响

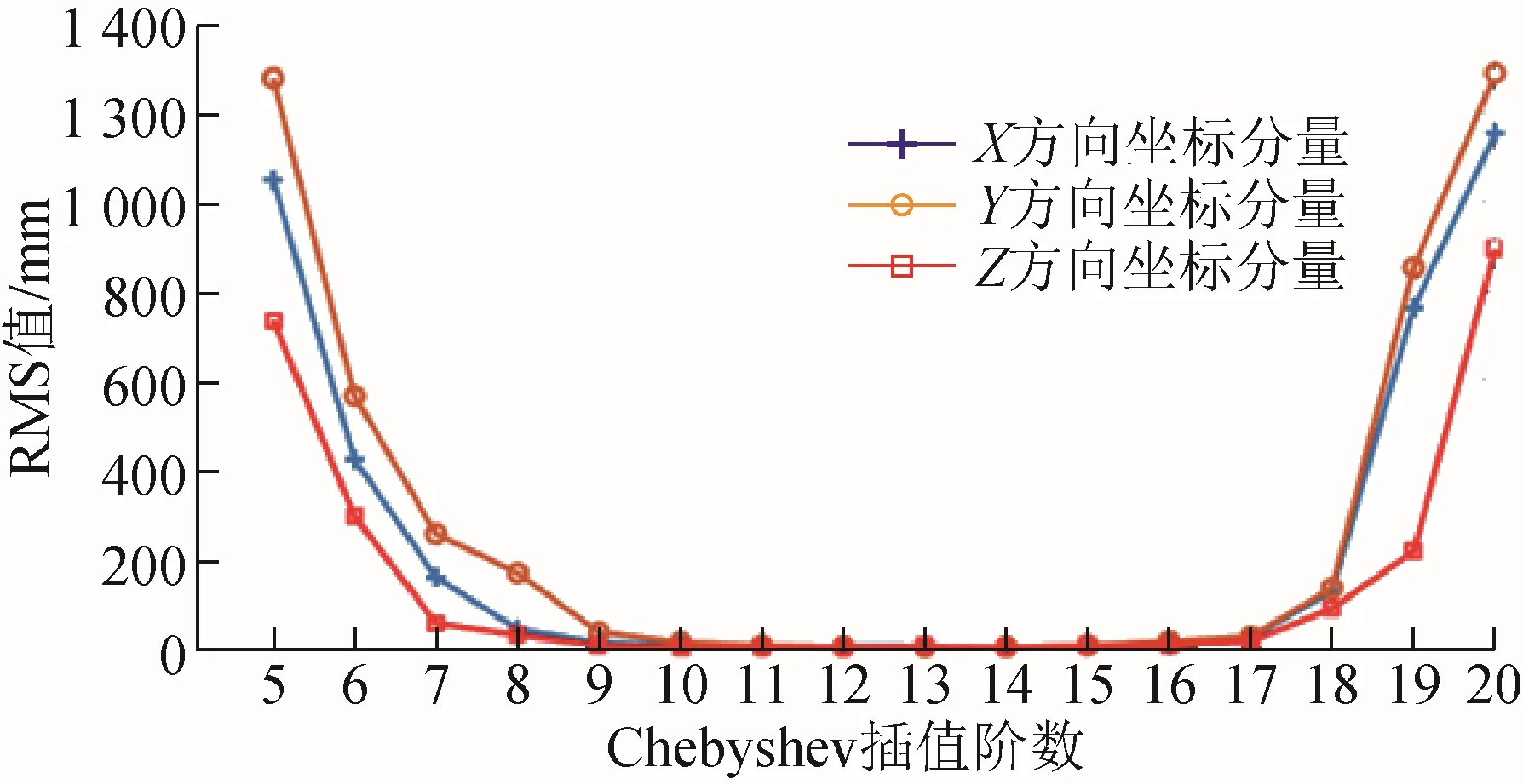
图7 不同阶数Chebyshev插值方法对MEO卫星的影响

表1 不同阶数滑动式Lagrange插值和Chebyshev插值对GEO卫星的影响

表3 不同阶数滑动式Lagrange插值和Chebyshev插值对MEO卫星的影响

2.1 GEO卫星精密星历内插精度分析

基于滑动式Lagrange插值方法对GEO卫星精密星历进行内插，由表1和图2可以看出：5~19阶滑动式Lagrange插值对GEO卫星精密在X、Y、Z方向坐标分量均可达到毫米级精度，当使用10阶滑动式Lagrange插值时，GEO卫星精密星历三维坐标分量精度达到最高，RMS值分别为0.92、0.84、0.52 mm；滑动式Lagrange插值阶数在5~10阶时，随着插值阶数的增加，插值精度随之提升，此时Z方向坐标分量插值精度最佳，X方向坐标分量插值精度最差；滑动式Lagrange插值阶数在11~20阶时，随着插值阶数的增加，插值精度反而降低，此时Z方向坐标分量插值精度最佳，X方向坐标分量插值精度最差。

基于Chebyshev插值方法对GEO卫星精密星历进行内插，由表1和图3可以看出：5~16阶Chebyshev插值对GEO卫星精密在X、Y、Z方向坐标分量均可达到毫米级精度，当使用 9阶Chebyshev插值时，GEO卫星精密星历三维坐标分量精度达到最高，RMS值分别为0.45、0.85、0.62 mm；Chebyshev插值阶数在5~9阶时，随着插值阶数的增加，插值精度随之提升，Chebyshev插值阶数在8~10阶时，GEO卫星精密星历三维坐标分量精度均达到亚毫米级精度，且精度相当；Chebyshev插值阶数在13~20阶时，随着插值阶数的增加，插值精度反而降低，此时X方向坐标分量插值精度最佳，Z方向坐标分量插值精度最差。对GEO卫星而言，与Chebyshev插值方法相比滑动式Lagrange插值方法有效避免“龙格”现象的产生。

图3 不同阶数Chebyshev插值方法对GEO卫星的影响

2.2 IGSO卫星精密星历内插精度分析

基于滑动式 Lagrange插值方法对 IGSO卫星精密星历进行内插，由表2和图4可以看出：8~17阶滑动式 Lagrange插值对 IGSO卫星精密在X、Y、Z方向坐标分量均可达到毫米级精度，当使用14阶滑动式Lagrange插值时，IGSO卫星精密星历三维坐标分量精度达到最高，RMS值分别为0.85、1.28、1.38 mm；滑动式Lagrange插值阶数在5~14阶时，随着插值阶数的增加，插值精度随之提升，此时X方向坐标分量精度最佳，Z方向坐标分量精度最差；滑动式Lagrange插值阶数在15~20阶时，随着插值阶数的增加，插值精度反而降低，此时X方向坐标分量插值精度最佳，Z方向坐标分量插值精度最差。

表2 不同阶数滑动式Lagrange插值和Chebyshev插值对IGSO卫星的影响

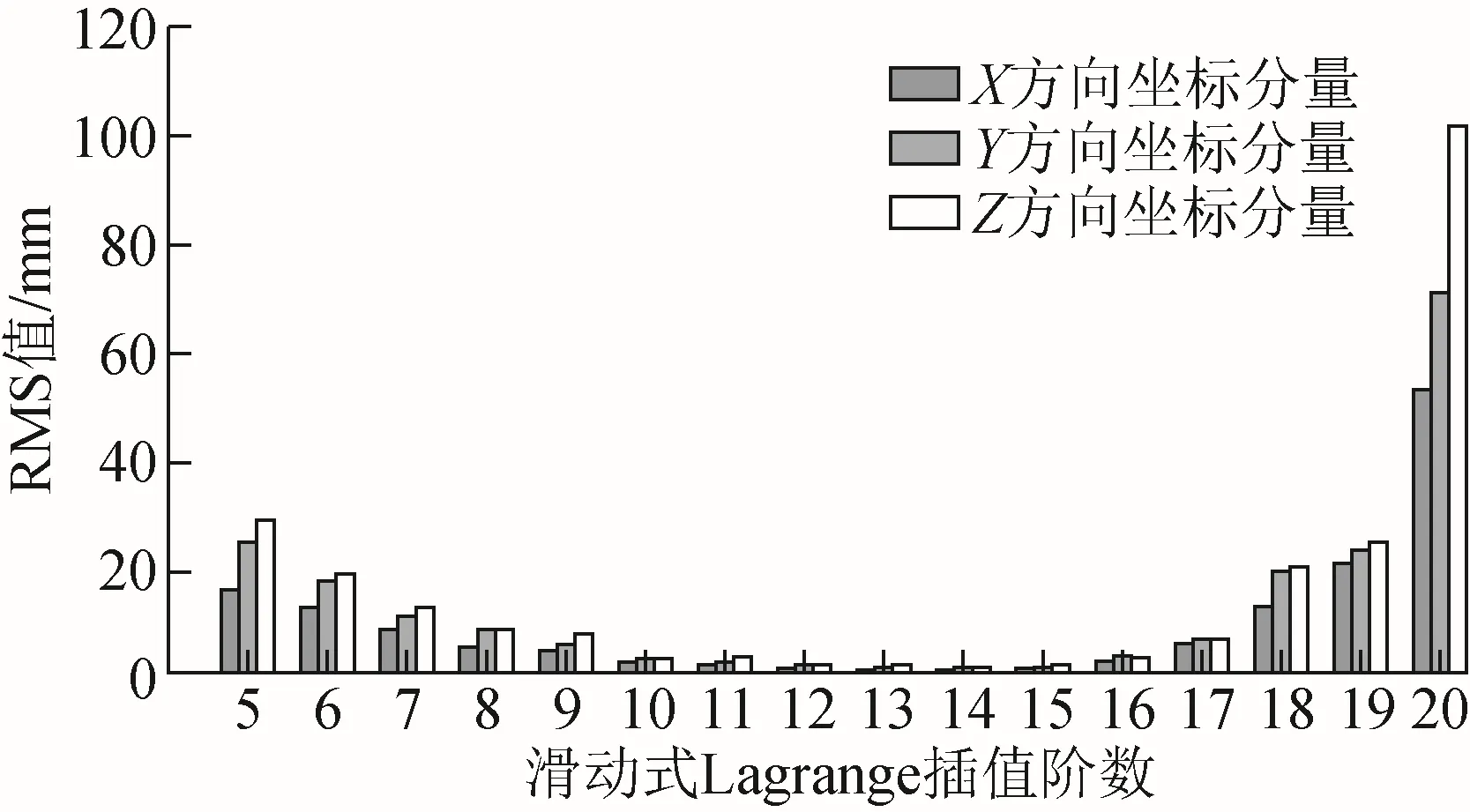
图4 不同阶数滑动式Lagrange插值方法对IGSO卫星的影响

基于Chebyshev插值方法对IGSO卫星精密星历进行内插，由表2和图5可以看出：10~17阶Chebyshev插值对IGSO卫星精密在X、Y、Z方向坐标分量均可达到毫米级精度，当使用 14阶Chebyshev插值时，IGSO卫星精密星历X方向坐标分量、Y方向坐标分量精度达到最高，RMS值分别为0.79、1.30 mm，当使用15阶Chebyshev插值时，IGSO卫星精密星历Z方向坐标分量精度达到最高，RMS值为0.62 mm，Chebyshev插值阶数在5~14阶时，随着插值阶数的增加，插值精度随之提升，Chebyshev插值阶数在15~20阶时，随着插值阶数的增加，插值精度反而降低；5~11阶时，Z方向坐标分量插值精度最佳，Y方向坐标分量插值精度最差。

图5 不同阶数Chebyshev插值方法对IGSO卫星的影响

2.3 MEO卫星精密星历内插精度分析

基于滑动式Lagrange插值方法对MEO卫星精密星历进行内插，由表3和图6可以看出：9~17阶滑动式Lagrange插值对MEO卫星精密在X、Y、Z方向坐标分量均可达到毫米级精度，当使用14阶滑动式Lagrange插值时，MEO卫星精密星历三维坐标分量精度达到最高，RMS值分别为0.79、1.41、1.15 mm；滑动式Lagrange插值阶数在5~14阶时，随着插值阶数的增加，插值精度随之提升，滑动式Lagrange插值阶数在 15~20阶时，随着插值阶数的增加，插值精度反而降低；滑动式 Lagrange插值阶数在 5~9阶时，Z方向坐标分量插值精度最佳，Y方向坐标分量插值精度最差，滑动式Lagrange插值阶数在 10~14阶时，X方向坐标分量插值精度最佳，Y方向坐标分量插值精度最差，滑动式Lagrange插值阶数在 15~20阶时，Y方向坐标分量插值精度最佳，X方向坐标分量插值精度最差。

图6 不同阶数滑动式Lagrange插值方法对MEO卫星的影响

基于Chebyshev插值方法对MEO卫星精密星历进行内插，由表3和图7可以看出：11~15阶Chebyshev插值对MEO卫星精密在X、Y、Z方向坐标分量可达到毫米级精度，当使用 11阶Chebyshev插值时，MEO卫星精密星历Z坐标分量精度达到最高，RMS值为3.22 mm，当使用13阶Chebyshev插值时，MEO卫星精密星历Y坐标分量精度达到最高，RMS值为 3.44 mm，当使用14阶Chebyshev插值时，MEO卫星精密星历Z坐标分量精度达到最高，RMS值为 3.34 mm；Chebyshev插值阶数在5~11阶时，随着插值阶数的增加，插值精度随之提升，Chebyshev插值阶数在 14~20阶时，随着插值阶数的增加，插值精度降低。对MEO卫星而言，与Chebyshev插值方法相比，滑动式Lagrange插值方法有效避免“龙格”现象的产生。

3 结束语

本文借助武汉大学IGS数据中心提供的BDS精密星历产品，基于滑动式 Lagrange插值和Chebyshev插值方法对三种类型轨道卫星进行精密星历插值分析，实验结果表明：滑动式Lagrange插值和Chebyshev插值方法对GEO卫星精密星历最佳可达到亚毫米级精度，对IGSO、MEO卫星精密星历最佳可达到毫米级精度，均可满足高精度导航定位的需求；与Chebyshev插值方法相比，滑动式 Lagrange插值方法有效避免“龙格”现象的产生；滑动式Lagrange插值和Chebyshev插值方法的阶数均不宜过高或过低，同一种插值方法对应不同卫星所达到最佳精度时阶数不同，同一卫星对应不同的插值方法最佳精度时阶数亦不相同。因此，今后在获取任意时刻BDS精密星历时，需针对不同卫星采取不同插值方法不同阶数以达到插值精度效果最佳的目的。