考虑输入饱和的直升机机动飞行LPV控制

李 硕, 张绍杰,*, 严 鹏, 张 涵, 鲁 可,2

(1. 南京航空航天大学自动化学院, 江苏 南京 211106; 2. 中国直升机设计研究所直升机旋翼动力学重点实验室, 江西 景德镇 333001)

0 引 言

直升机机动飞行是指直升机在作战飞行时灵活改变直升机的速度、方向、高度、姿态的动作,使其完成一系列从有限机动性到迅猛机动性的全部飞行科目。ADS-33E-PRF是一种以任务为导向的直升机驾驶品质规范,一共给出了23种机动飞行科目,并为所有的科目都合理规划了需要满足的性能指标要求。为了对机动飞行进行模拟仿真,需要用数学描述的方法界定飞行轨迹的边界条件,生成可供仿真的导航模型。其中,在不考虑驾驶员建模的情况下,逆仿真方法是直升机机动飞行数值模拟的主要手段。其本质是根据驾驶品质规范划定的飞行轨迹要求,在直升机运动学方程中附加边界条件约束,使得求解方程时具有唯一解。

输入饱和在直升机机动飞行的控制系统中是一个不可忽视的问题。当直升机的姿态或速度的指令信号输入值较大时,容易超出执行器的作用范围,导致控制器输出与执行器输出不一致,从而引发系统性能下降甚至出现发散的问题。文献[9]中,在执行机构饱和约束下,针对直升机这种开环不稳定系统,提出了一种两步法抗饱和控制方法。文献[10]中,针对超空泡航行体在运动过程中面临的执行器饱和问题,通过Lyapunov方法,基于多面体理论和线性矩阵不等式的约束,设计了一种状态反馈控制器。文献[11]针对三自由度直升机,提出了一种基于混合性能和线性二次调节器的鲁棒控制器,将控制输入间接约束在代价函数中。虽然上述文献对输入饱和的研究已有一定的成果,但基于LPV模型对直升机机动飞行的输入饱和研究较少。

为使直升机机动飞行的输入出现饱和时仍然能够跟踪机动飞行轨迹,本文基于参数依赖的Lyapunov函数和集不变性,提出了一种状态反馈控制方法。首先在动力学方程的基础上选用能表征直升机非线性特性的状态量作为时变参数,采用雅克比线性化方法建立了线性变参数(linear parameter varying, LPV)纵向模型。为了对时变参数进行跟踪控制,对LPV纵向模型进行了增广变换。基于吸引域与不变集理论和参数依赖Lyapunov方法,结合参数化线性矩阵不等式(parameterized linear matrix inequalities,PLMI)提出了一种状态反馈控制器。利用松弛变量技术将难以求解的PLMI条件转换成易于求解的线性矩阵不等式(linear matrix inequalities,LMI)条件,通过求解LMI得到直升机机动飞行在输入饱和时保持稳定追踪的控制律。仿真结果表明闭环系统能够渐近跟踪给定指令,且能够有效地实现抗饱和补偿。

1 直升机纵向LPV模型与机动飞行的轨迹描述

1.1 LPV模型

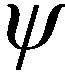
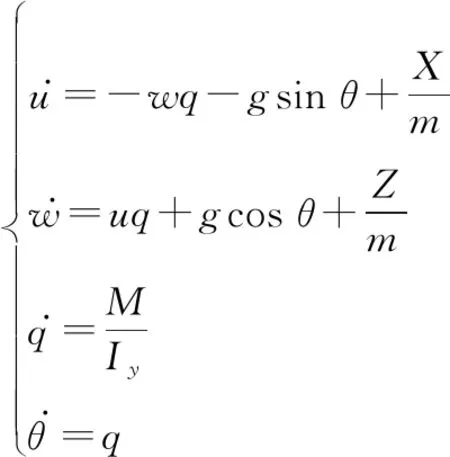
(1)

式中:表示直升机总质量;为直升机沿前向机体轴的线速度;表示沿直升机垂向机体轴的线速度;是俯仰角速率;为俯仰角;惯性矩用来表示;是俯仰力矩;,分别为作用于直升机机体轴和的合力。

常用的建立与非线性模型动态接近的LPV模型的方法有3种:雅克比线性化、状态变换和函数替换法。由于雅克比线性化法可以在任意平衡点处线性化,易于在非线性模型平衡点处进行线性化处理,因此本文选择雅克比线性化方法,然后对多个平衡点采用数据拟合法建立LPV模型。

本文参考文献[22]中建立的LPV模型,选取调度参数,,的高阶次幂,即

=[,,,,,,,,,,]

(2)

使用其仿射参数依赖形式的LPV模型:

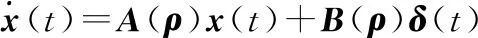
(3)

式中:=[,,,],=[,],为纵向周期变距,为旋翼总距,且

()=+++++++
++++

(4)

()=+++

(5)

式中:(=0,1,…,11),(=0,1,2,3)为适当维数的常数向量。

1.2 机动飞行轨迹描述

悬停科目是ADS-33E-PRF中规定的直升机任务科目基元,该科目考察了直升机从平飞到悬停的能力。基于本文建立的LPV纵向模型,忽略直升机横侧向部分的要求,规定飞行轨迹保持在-平面内,侧向速度总为0。

考虑到任务科目的动作要求和性能要求,对直升机机动飞行的轨迹进行数学描述,根据图1给出的轨迹路线图和ADS-33E-PRF中给出的期望性能,选择通用机型在目视良好的状态下,分时段对直升机的轨迹进行描述。

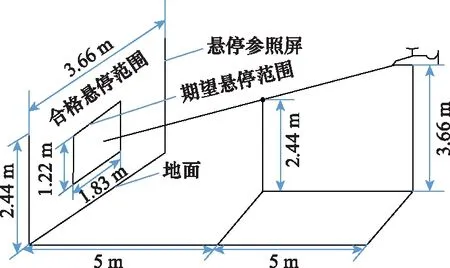
图1 悬停科目试验轨迹示意图Fig.1 Schematic diagram of hovering subject test trajectory

任务科目要求直升机在低于6.096 m的高度下,以3.087～5.144 m/s的地面速度启动。本文设定直升机以初始高度为3.66 m、初始速度为4 m/s的水平前飞状态进入该机动。=0 s时刻开始减速下降,产生负的前向加速度,给定地面参照标为2.44 m,减速至=5 s时,悬停在1.22 m处,使得前飞速度=0 m/s,然后保持悬停状态至时间=35 s。

将直升机的垂向位移用()表示,则-阶段,()满足以下边界条件:

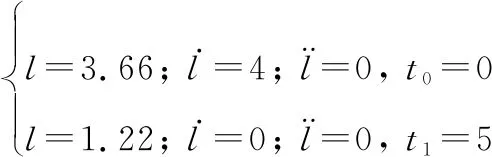
(6)

由边界条件,可将()表示为5次多项式:

()=+++++

求解可得

()=-0004 7+0058 6-0195 2+366

(7)

将直升机的水平位移用()表示,则-阶段,()满足以下边界条件:

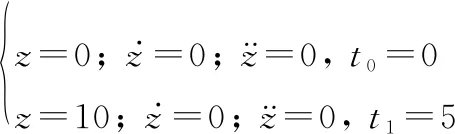
(8)

同理可解

()=0016-016+4

(9)

1.3 模型的增广

第12节给出了悬停科目的机动飞行轨迹数学描述,可以看出,悬停科目需要速度分量和速度分量进行跟踪控制。因此,需要考虑对参考输入的跟踪控制问题,记指令信号为()=[,],系统的输出为

()=+()

(10)

式中:

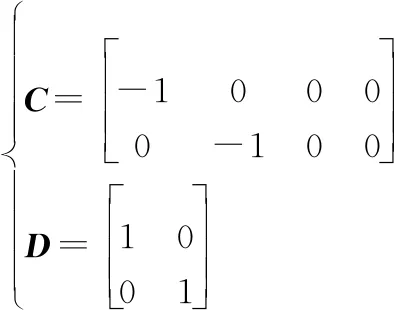
(11)

则系统控制目标为

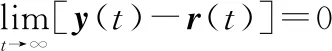
(12)

将跟踪误差积分项

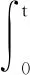
(13)

与直升机纵向LPV模型(见式(2))联合,得出增广系统:

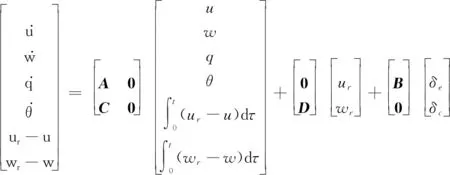
(14)

2 控制律设计

2.1 PLMI条件

考虑如下具有仿射参数依赖的LPV系统:

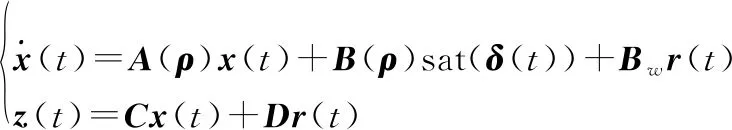
(15)

式中:=[,,…,]为可时刻检测的变参数,且在如下给定范围变化:

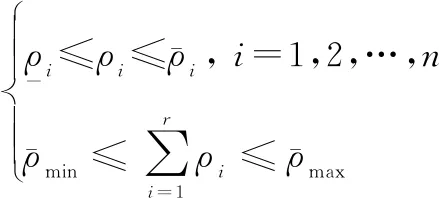
(16)

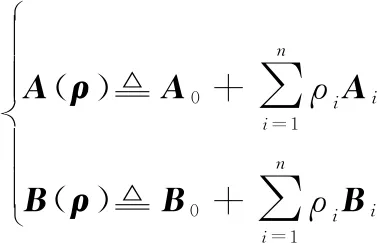
(17)

()是系统的输入指令信号;()为性能输出;()为系统的控制输入;sat(·)代表控制输入的饱和函数,定义为

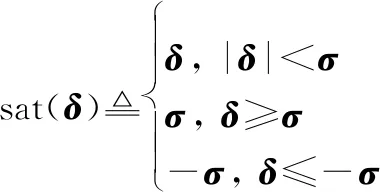
(18)

式中:表示饱和阈值。为方便书写,将下文中()省去。

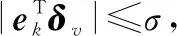
(19)

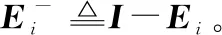
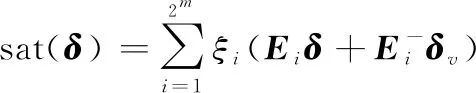
(20)

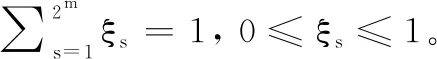
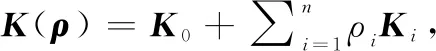
(1) 当控制输入信号饱和时,对于∈,闭环系统的轨迹必须有界。

(2) 控制性能目标是让闭环系统增益尽可能小,或使其小于一给定值,即有最小值>0,使得

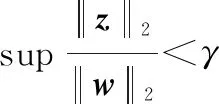
(21)

定义对称多面体

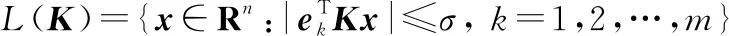
如果对于=1,2,…,,控制输入均未达到饱和,则∈()。定义()=,>0,若存在正实数,则定义椭球体

(,)={∈:≤}

(22)

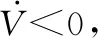
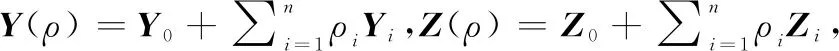
min log(det())

使得

(23)

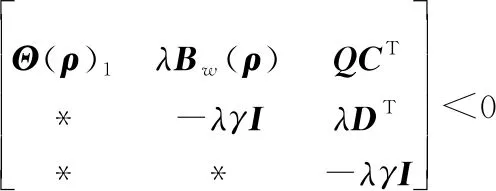
(24)

式中:

()=()

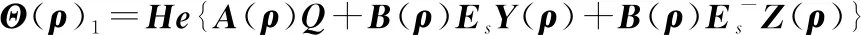
(25)

能够使闭环系统渐近稳定并具有增益。

选取椭球体(,)上的Lyapanov函数

()=()()

(26)

式中:为常数矩阵。定义椭球体

(,)={∈:≤}

(27)

可将单位椭球体表示为

(28)

式(28)中椭球体是一个正不变集,意味着对任何初始条件,若满足∈(,),则当≥,()∈(,)。

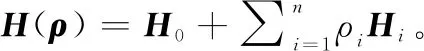
那么

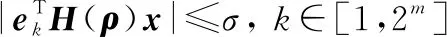
(29)

进一步,对∈[1,2],式(29)可变换为

(30)

且有

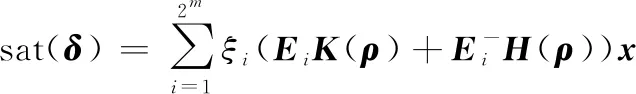
(31)

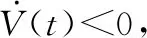
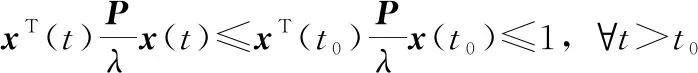
(32)

由于()定义在椭球体上,有()∈(,),∈()。令

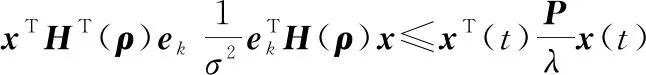
(33)

对不等式变换,两边省略。利用Schur补定理,且两边同时乘diag[,λ],可得到不等式(23)。接下来对式(24)进行证明。

若有以下不等式:

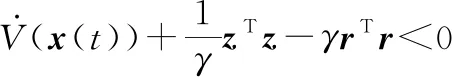
(34)

成立,则设计条件2中的不等式(21)可以被验证。

进一步,由式(20),式(34)可写成

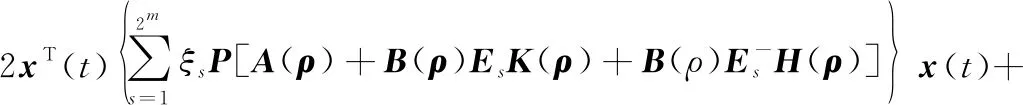
(35)

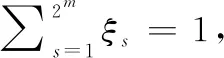
(36)

由于式(36)的形式是双线性矩阵不等式,因此可以通过前后相乘[,,]进行全等变换,同时整个矩阵乘。得到公式

(37)

令

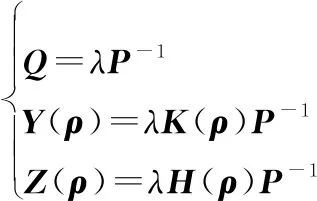
(38)

从而得到式(24)。

通过对椭球体(/λ)，即对()进行最优求解，从而可使系统初始条件的允许范围最大化。至此定理1证毕,得到控制器设计的PLMI条件。

证毕

2.2 LMI条件

上述PLMI条件涉及无穷多个LMI条件,因此求解控制器的任务是复杂难解的。为了克服这一点,使用松弛变量技术将第2.1节中求出的PLMI条件转换为时变参数的LMI条件。

基于松弛变量技术,时变参数的约束(16)可以转变为

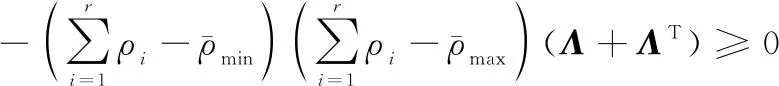
(39)

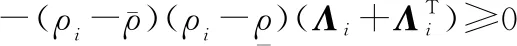
(40)

式中:矩阵∈×,∈×满足

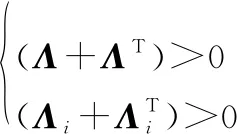
(41)

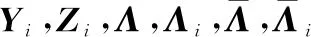
对于PLMI条件式(23),结合式(39)～式(41),有

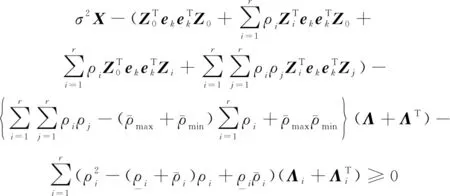
(42)

定义向量()=[,,…,],式(42)可写为

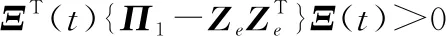
(43)

式中:

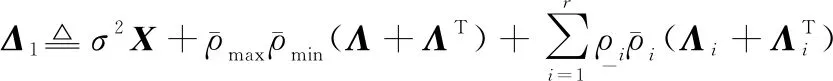
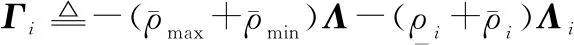
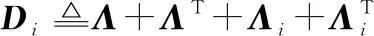
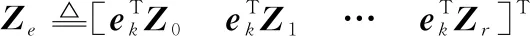
由Schur补定理,式(43)等价于

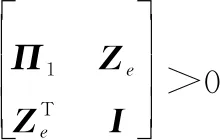
(44)

同理对于PLMI条件式(24),结合式(39)～式(41),有

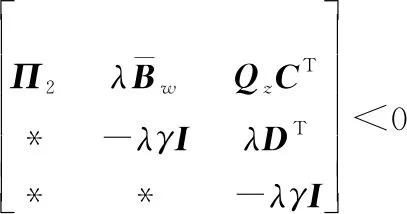
(45)

式中:

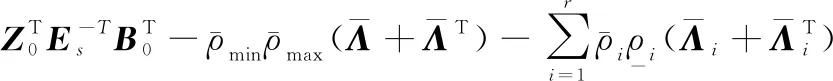
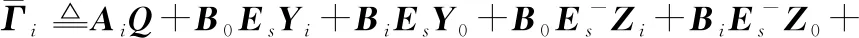
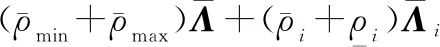
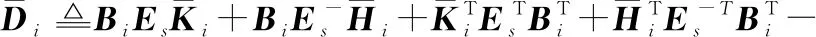
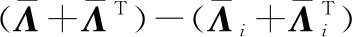
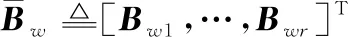
证毕

3 仿真分析

参考文献[22]中给定的直升机数据,通过定理2中LMI对LPV模型式(10)、式(14)进行输入饱和的控制律求解。同时给定时变参数的范围为

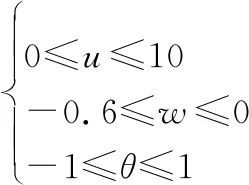
(46)

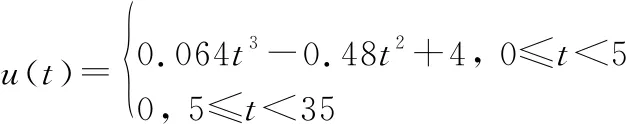
(47)

(48)

仿真得到直升机模型的速度分量和速度分量响应跟踪曲线如图2和图3所示。垂向位移()和前向位移()的响应跟踪曲线如图4和图5所示。从图2和图3可以看出,速度分量和速度分量以较快的响应速度跟踪了参考输入,即直升机能够在规定时间范围内完成平稳的悬停过渡。

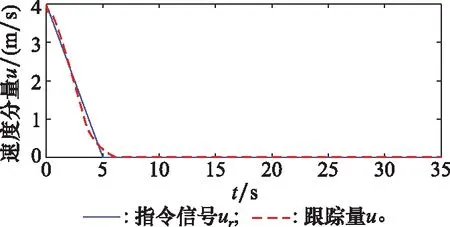
图2 速度分量u的响应跟踪曲线Fig.2 Response tracking curve of velocity component u

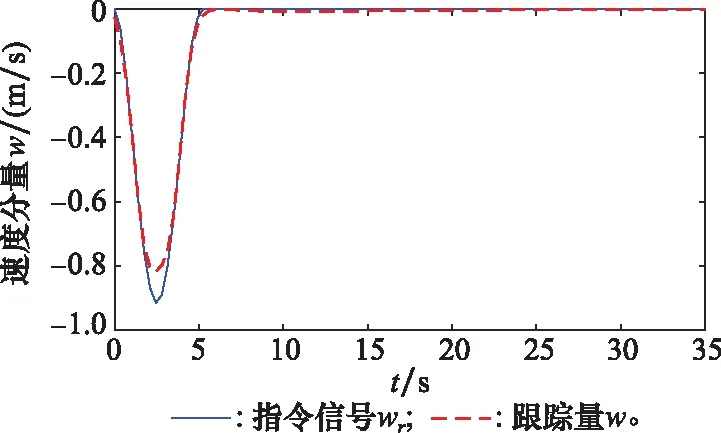
图3 速度分量w的响应跟踪曲线Fig.3 Response tracking curve of velocity component w

图4 垂向位移l的响应跟踪曲线Fig.4 Response tracking curve of vertical displacement l

图5 前向位移z的响应跟踪曲线Fig.5 Response tracking curve of forward displacement z

ADS-33E-PRF中给出了不同类型的直升机的期望性能与合格性能。对于通用机的要求是高度偏差保持在正负0.61 m内,相对于地面点的纵向偏差保持在0.91 m内。对于本文选取的通用机型,从图4可以看出,垂向位移偏差为0.23 m,在合理的误差范围内,有较为理想的跟踪效果。表明通用直升机在进行悬停机动时可以保持高度偏差在期望性能范围内,30 s内也能够保持稳定悬停,从图5可以看出,直升机在保持悬停的时间段内,前向位移偏差为0.674 m,能够保持在0.91 m内,满足期望性能要求。

考虑输入饱和时,控制器输入量的仿真曲线如图6和图7所示。从图中可以看出,所设计的抗饱和控制器在对指令信号进行跟踪的同时,输入量可保持在所设定的-0.1～0.1 m范围内,实现了抗饱和补偿。实验结果表明基于输入饱和控制器,直升机可以在一定性能范围内完成悬停科目的试飞。

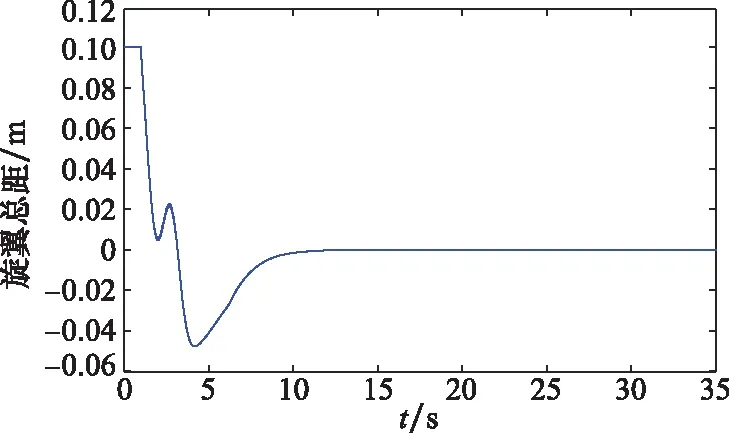
图6 旋翼总距Fig.6 Collective pitch

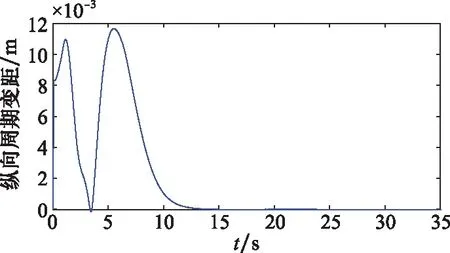
图7 纵向周期变距Fig.7 Longitudinal cyclic coefficient

4 结 论

本文以直升机为研究对象,针对直升机机动飞行过程中遇到的输入饱和问题,在动力学方程的基础上选用能表征直升机非线性特性的状态量作为时变参数,采用雅克比线性化方法建立了LPV纵向模型。且为对时变参数进行跟踪控制,对参考文献[22]提供的模型进行了增广变换。通过求解定理2中的LMI条件得到了直升机机动飞行在输入饱和时可保持稳定追踪的控制律。仿真结果表明闭环系统能够渐近跟踪给定指令,且能够有效地实现抗饱和补偿。