环Fq[v]/上循环码的迹码与子环子码
李 娟( 山东理工大学 数学与统计学院,山东 淄博 255049)
在编码理论中,子域子码是一类重要的线性码.常见的子域子码有:Hamming 码,Goppa 码等. Delsarte[1]给出有限域上子域子码与迹码的关系. 然而, 对于一般线性码,子域子码与迹码的计算较复杂.Gao 等人[2]利用线性递归序列与循环码的关系,给出有限域上循环码的子域子码与迹码的生成多项式. 编码学家Hammons 等人[3]发现一些性能良好的非线性码可以看做四元环Z4上一些循环码的二元Gray象. 近几年,有限非链环上的纠错码理论的研究也吸引了编码学者的关注. Jitman 等人[4]给出有限非链环Fpk+uFpk+…+um-1Fpk上码长为ps的常循环码的结构. Yildiz 和Karadenniz[5]研究了环F2+uF2+vF2+uvF2上的线性码和循环码. 高健等人[6]中给出环Fp[v]/
1 环Fq[v]/上的线性码
设R=Fq[v]/
R={a0+a1v+…+am-1vm-1|ai∈Fq,i=0,1,…,m-1}.
另外,由于m-1|(p-1),则多项式vm-v=(v-k0)(v-k1)…(v-km-1),其中k0,k1,…,km-1∈Fq,k0=0.
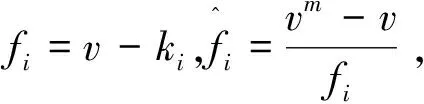

R=e0R⊕e1R⊕…⊕em-1R=e0Fq⊕e1Fq⊕…⊕em-1Fq,
且
R≅Fq[v]/
因此,环R中任意元素r可唯一表示为
r=e0r0+e1r1+…+em-1rm-1.
其中ri∈Fq,i=0,1,…,m-1.
令R=Fp[v]/
因为q=pl,则|f|=l, 且
易证,该映射是满射.
定义1设Rn={(c0,c1,…,cn-1)|ci∈R,0≤i≤n-1},Rn上的任意一个非空子集C称为R上长度为n的码.特别地,如果C是Rn的R-子模,则称C是R上码长为n的线性码.
定义2对线性码C中任意一个码字(c0,c1,…,cn-1),如果有(cn-1,c0,…,cn-2)仍是C中码字,则称C是R上码长为n的循环码.
设R[x]为R上以x为变量的多项式环,且码字(c0,c1,…,cn-1)的多项式表示为c0+c1x+…+cn-1xn-1,则Rn与商环 R[x]/
对任意的i=0,1,…,m-1,定义集合

则有:1)集合Ci是有限域Fq上码长为n的线性码.
2)线性码C可唯一表示为
C=e0C0+e1C1+…+em-1Cm-1.
3)设G是C的生成矩阵,则C作为Rn的Fq-子空间,矩阵G可表示为
其中G0,G1,…,Gm-1分别是C0,C1,…,Cm-1在有限域Fq上的生成矩阵.
引理1[6]线性码C=e0C0⊕e1C1⊕…⊕em-1Cm-1是环R上的循环码,当且仅当对任意的i=0,1,…,m-1,Ci是有限域Fq上的循环码.
由引理1,有以下结果:

2 环Fp[v]/上的迹码
令{α0,α1,…,αl-1}是Fpl在Fp上的一组基,则{α0,α1,…,αl-1}也是R在R上的一组基.定义映射
其中i=0,1,…,l-1,且cj∈Rn.显然hi是环R上的线性映射.
引理3令C是环R上码长为n的线性码,则对任意i=0,1,…,l-1,hi(C)=Tr(C).


故,hi(C)=Tr(C).
定理1令C是环R上码长为n的循环码,{s1,s2,…,sk}是循环码C的极小生成元集,则{hi(sj),0≤i≤l-1,1≤j≤k}生成迹码Tr(C).

其中ρtri∈R.于是,
从而,对任意的0≤i≤l-1,有下面等式成立
由引理3知该定理成立.
通过定理1,可得出环R上循环码的迹码.

则循环码C的迹码
Tr(C)=
证明令C=
S1∪S2∪…∪Sm-1.
其中
令
显然,
其中0≤j≤l-1,0≤i≤m-1.
因此,由定理1, 可得出Tr(C)的生成元集为
下面令
则,
例1令R=F5+vF5+v2F5,其中v3=v.令f(x)=x2+4x+2是F5上的二次本原多项式,则R=R[x]/
Tr(C)=<(1-v2)(x2+2)+3(v2+v)+3(v2-v)(x2+x+1)>.
3 子环子码
令C是环R上码长为n的线性码,C的子环子码用C|R表示,即C|R=C∩Rn. 若环R上码长为n的线性码C是循环码,易证其子环子码也是循环码. Martinez-Moro 等人[1]给出Delsarte Lemma, 即有限链环上线性码的迹码与子环子码的关系,下面给出有限非链环R上两者的联系.
类似于文献[1],可以给出有限非链环上的Delsarte引理。证明过程类似于文献[1]中的证明过程.
引理4[Delsarte 引理]
令C是环R上码长为n的线性码, 则
(C|R)⊥=Tr(C⊥).
根据引理4,给出有限非链环R上,循环码的子环子码的生成元.
推论2令C是环R上码长为n的循环码,其中
C=
令



证明由C=

由推论1,可得出
Tr(C⊥)= em-1gcd(g0,m-1(x)*,g1,m-1(x)*,…,gl-1,m-1(x)*)>. 再由引理4,C|R=(Tr(C⊥))⊥, 从而 例2令R=F3+vF3+v2F3,其中v3=v.令f(x)=x2+2x+2是F3上的二次本原多项式,则R=R[x]/ Tr(C)=<(1-v2)(x2+1)+2(v2+v)(x2+x+2)+2(v2-v)(x2+2x+2)>. 由引理4得 [1]DELSARTE P. On subfield subcodes of modified Reed-Solomon codes [J]. IEEE Transactions on Information Theory, 1975, 21(5):575-576. [2]GAO Z H, FU F W. Linear recurring sequences and subfield subcodes of cyclic codes[J]. Science China Mathematics, 2013, 56(7):1 413-1 420. [3]HAMMONS A R, KUMAR P V,CALDERBANK A R, et al. The-linearity of kerdock, preparata, goethals, and related codes [J]. IEEE Transactions on Information Theory, 1994, 40(2): 301-319. [4]JITMANA S,UDOMKAVANICHB P. On the structure of constacyclic codes of lengthps overFpk+uFpk+…+um-1Fpk[J]. International Journal of Algebra, 2010, 4(11): 507-516. [5]YILDIZ B, KARADENIZ S. Self-dual codes overF2+uF2+vF2+uvF2[J]. Journal of the Franklin Institute,2010,347(10):1 888-1 894. [6]高健, 王现方, 施敏加, 等. 环Fp[v]/


