基于Inventor的多次曲线创建及其在叶片泵设计中的应用

谢红太，党小刚(西安铁路局 西安动车段，陕西 西安 710016)

计算机辅助设计技术中，准确快速地描述空间多次曲线显得极为重要.目前，普遍采用通过XYZ坐标点构建或通过可视化语言VBA等编程控制构建多次复杂曲线.Autodesk Inventor是一款面向机械设计的三维设计软件，它融合了当前CAD所采用的最新技术，具有强大的参数实体造型能力，智能的帮助系统，简单而直观的设计环境，快速装配显示，自适应装配系统以及辅助协作设计等优点，尤其在高次空间曲线和空间曲面的智能化参数化设计以及现代机械加工及模拟仿真分析方面[1-3]更为准确便捷.

以SolidWorks软件辅助设计为例，其对复杂高次特殊曲线的建模只能依靠笛卡尔坐标系中参数繁多的直角坐标方程进行搭建，本文以其他三维软件中实现较困难的双作用叶片泵定子内高次曲线为基础[4-5]，展开对Inventor表达式曲线的再运用及优势说明.

1 高次曲线在Inventor中的创建方法

1.1 建立高次函数模型

在工业制造领域中，对于一些加工表面形位精度要求较为严格的使用场合，多采用高次曲线控制构建外表面的形式以满足其相关的机械精度要求和运行稳定性及平稳性要求.例如，双作用叶片泵叶片与定子内六次曲线配合时可使其叶片受力状况最佳，航天飞行器的涡轮叶片设计等都大多采用性能较高的多次曲线.

高次方程也称为整式方程，其一般形式为：y=kxm,(m≥2)，其中x为自变量，y为因变量，k为系数，m为幂级数.在包含有两个变量x，y的二维直角坐标系中所取点描绘出的图形即此高次方程所对应的高次曲线.本文首先以二次函数曲线为例对Inventor中二维曲线创建的两种方法进行探究，令二次函数：fx=0.1x2+0.1x-2 .

1.2 利用样条曲线对二次离散点进行拟合

1)在Excel中列举计算有限二维离散点

在此利用Microsoft Office Excel对如上fx二次函数曲线进行区间内的离散点确定.在Excel表格中输入fx对应的两个关系变量，即自变量x，因变量y，并对自变量x给定一个闭区间[-10,10]，并分别列出闭区间中的21个特殊整数值，在Excel表格相应单元格中编写fx函数关系fx=0.1x2+0.1x-2,并将其应用到因变量y所在列中，系统对其进行自动处理列出相应的计算离散数组，结果见表1.

表1 fx在Excel中x，y所对应的二维坐标点
Tab.1 fxin Excel x, y 2d coordinates of the point

序号123456789101112131415161718192021x-10-9-8-7-6-5-4-3-2-1012345678910fx(y)75．23．62．210-0．8-1．4-1．8-2-2-1．8-1．4-0．8012．23．65．279

2)将二维离散点导入Inventor草图环境中

Inventor草图设计集目标参数化与变量化设计于一体，整个草图环境中功能齐全，能实现智能化约束与驱动.在功能区中将Excel点插入模块，设定并调整相应的单位及接口后即可实现Excel表格中所设定的fx函数所对应的21组二维离散数组[x,y]的导入，如图1所示.并对图中的21个离散点进行锁定约束，确定其在外界参数调整下处于草图xoy坐标系的位置不变.

用Inventor中的样条曲线拟合fx二次曲线.样条的概念来源于制图技术，即让富有弹性的线条(称为样条)通过一组点，得到光滑的曲线.目前使用的样条曲线主要有二次样条曲线和三次样条曲线，其中大多Inventor高版本软件中的样条曲线为三次样条曲线.三次样条曲线克服了二次样条曲线的缺点，即最前面的两个点所对应的线段为直线连接，最后一个曲线区间的摆动过大；也克服了不常用的高次样条曲线有时可能会造成的龙格现象.采用样条曲线进行插值拟合完成的平面fx二次曲线如图1所示，对其进行长度检测为l1=29.624mm.

图1 样条曲线拟合的fx二次曲线Fig.1 Spline curve fitting fx quadratic curve

1.3 利用表达式创建二次曲线

1)fx表达式的参数化方程设定

按照如上所述的二次曲线模型fx=0.1x2+0.1x-2，建立Inventor草图参数化设计中所特有的t参数模型，即

(1)

Inventor中特别规定，曲线的创建必须在某一限定的有限闭区间之内，即

(2)

2)在Inventor草图中创建fx二次曲线模型

选择笛卡尔坐标系，以t作为参变量，x(t)、y(t)为因变量，分别对照设定参函数的上下闭区间tmin、tmax，即可完成整个二次曲线的创建，结果如图2所示.

图2 Inventor中的表达式曲线fxFig.2 fx expression curve of Inventor

同样，将该二维曲线转换到三维xyz空间中，利用长度检测工具测得曲线长度l2=29.624mm.由上述可知，通过导入Excel参数表和三次样条曲线拟合的方式创建的fx二维曲线和直接采用表达式曲线创建的fx二维曲线在闭区间内的弧长l1=l2=29.624mm，则说明在Inventor表达式曲线的建模机制中正是采用了三次样条曲线和有限坐标点拟合的方式.

2 模型fx的积分学研究

利用对弧长曲线积分的计算法，设f(x,y)在曲线弧L上有定义且连续，L的参数方程为

(3)

存在，且

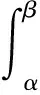
由此对上述fx函数进行在区间[-10,10]上的曲线积分，从而求出其准确的弧长值l0.在此把x看做y的参变量，利用弧长的曲线积分计算定理，求其弧长l0，即

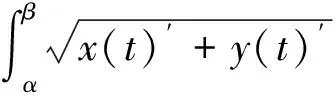
(4)

有关曲线积分的计算在此不再赘述，分别带入计算得理论弧长l0≈29.618mm.通过数学积分对fx二维曲线在闭区间上的弧长计算得l0≈29.618mm，与通过Inventor创建的fx二维曲线弧长l1=l2=29.624mm的误差仅为Δ=0.02%，故由Autodesk Inventor 中所提供的创建曲线的这两种方法，在数模仿真分析计算中有着一定的现实意义，也为实际设计生产运用提供了一个较为可靠的技术方案.

3 基于Inventor的叶片泵定子内曲线的创建

目前，叶片泵是大功率机械化系统中使用较广的动力原件之一，定子和叶片作为叶片泵核心受力构件，其内曲线的研究设计有着不言而喻的意义.市场上常见的双作用叶片泵的定子内曲线形式多为余弦曲线、正弦曲线、 等加速等减速曲线等.近几年的研究发现，相比其他形式的曲线，高次内曲线无论在速度、加速度及加速度变化率等液压系统性能方面更具优势，但其中一个难点就是定子内部特殊高次曲线的数模创建[6].

3.1 双作用叶片泵定子内曲线的数学模型

为了更为直观地运用Inventor高次曲线的建模机制，在此选择YB型双作用叶片泵为雏形，所不同的是定子内曲线不是完整的曲线所直接组成，而是由4段过渡曲线、两段小圆弧r、两段大圆弧R连接而成，依据相关机械制造标准，定子外形为直径D=φ65mm的普通圆柱面；定子内曲线的小圆弧半径r=26mm，大圆弧(0°叶片倾角时)半径R=27.682mm，大圆弧和小圆弧所对应的4段圆弧角均相等且为α=36° ，4段特殊高次曲线所对应的圆弧角为β=54°.

由六次曲线极坐标方程的标准形式ρ(φ)=a0+a1φ+a2φ2+a3φ3+a4φ4+a5φ5+a6φ6及φ=0 ,φ=β两边界条件可求出0°叶片倾角时对应六次曲线的极坐标方程

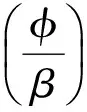
(5)

根据此边界条件，依次将r=26mm，R=27.682mm，β=54°，代入推导出0°叶片倾角时六次曲线的极坐标方程，即

(6)

3.2 双作用叶片泵定子内缘的建模设计

进入Autodesk Inventor草图设计环境中，其中fx表达式曲线为用户提供了两种曲线设计环境，即笛卡尔坐标系和极坐标系，针对式(6)所表示的定子内曲线4段特殊六次曲线的极坐标参数方程，切换到极坐标系状态下进行参数方程的创建.

(7)

系统根据式(7)所建定子内曲线高次曲线段的极坐标方程，拟合出该曲线如图3(a)所示.依次创建分别连接于六次曲线段两侧的小圆弧段和大圆弧段，再分别镜像得到整个定子内曲线模型如图3(b)所示，然后在Inventor环境中拉伸叶片泵定子草图区域即可完成定子三维模型的创建[7-8].

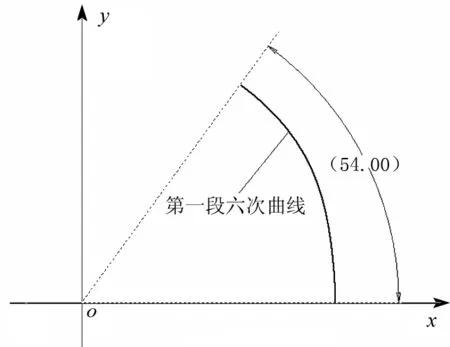
(a)第一段六次曲线

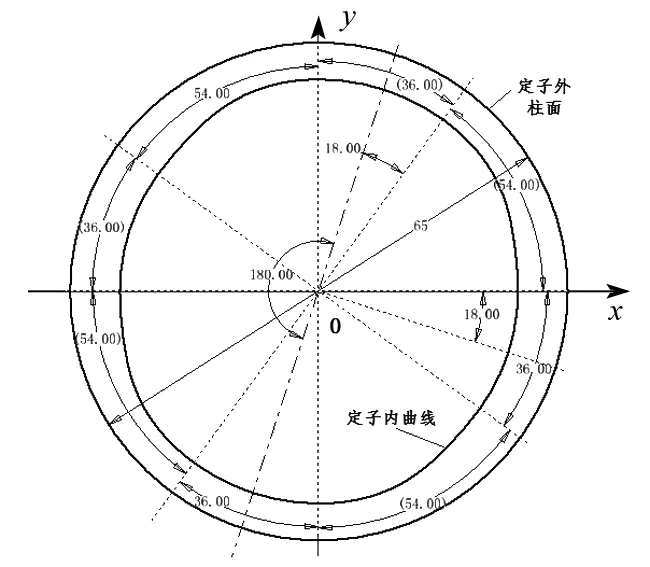
(b)定子内外曲线生成图3 定子内曲线模型的创建Fig.3 The creation of stator curve model

上述fx极坐标方程式(6)的创建与Inventor中为用户提供的fx表达式曲线双坐标系建模机制相适应，避免了在其他三维软件中(例如SolidWorks)必须将极坐标参数方程转换成直角坐标参数方程的弊端，而且由于两坐标系转换过程中存在正余弦函数以及无限不循环数π的参入，导致建模结果出现或大或小的误差，影响后续的研究.

4 结束语

应用Inventor软件对高次复杂曲线提出两种不同性质的创建方法，其中基于Microsoft Office Excel的曲线建模机制采用二维及多维数组点的创建提取，并导入到Inventor草图环境中利用样条曲线进行拟合，得到所需的近似曲线.此方法适合于Excel大数据的曲线分析建模处理，没有确切的函数关系表达式，较为方便灵活.对于fx表达式曲线的建模机制，采用可视化参数化的函数库作为基础，能准确识别常用函数及复杂对应关系式，如Inventor为用户提供了极坐标和笛卡尔坐标两种曲线参数表达形式，其中极坐标参数方程的表示对工业生产制造领域中特殊曲面、曲线的准确快速创建有着不可替代的意义.

[1]张华科，程从山.Autodesk Inventor Professional8命令详解及实践教程[M].北京：机械工业出版社，2005.

[2]童秉枢，易素君，徐晓慧.工程图学中引入三维几何建模的情况综述与思考[J].工程图学学报，2005(4)：130-135.

[3]王静，刘焜，程久平，等.Inventor在工程图学教学中的应用探索 [J].工程图学学报，2009(1):136-142.

[4]刘潇潇，任牟华，车军，等.叶片泵叶片倾角和定子内曲线对叶片受力的影响[J].兰州交通大学学报，2015,34(6):126-130.

[5]SRIVASTAVA S，ROY A K，KUMAR K. Design of a mixed flow pump impeller and its validation using FEM analysis[J]. Procedia Materials Science，2014,14:181-187.

[6]陈伯雄.Inventor R8应用教程——机械设计实战[M].北京：清华大学出版社，2004.

[7]陈定方，罗亚波.虚拟设计[M]. 北京：机械工业出版社，2004.

[8]杜峰波，穆希辉.基于Inventor的三维实体造型设计[J].湖北汽车工业学院学报，2003(4):8-10.