太阳影长定位的误差分析及在视频数据中的应用

田新宇，苗 枫，刘卓澜(.中南大学 数学与统计学院，湖南 长沙 40083；. 中南大学 机电工程学院，湖南 长沙 40083)

2015年“高教社杯”全国大学生数学建模竞赛A题“太阳影子定位”要求通过分析提供的影长测量数据及视频中物体太阳影子的变化，确定视频拍摄的地点和日期.而后，国内学者先后提出了利用影长与位置关系进行反演定位的模型[1-3]，但是针对定位精度的研究较少，对精度的提高仅针对于模型优化的算法研究.例如，于鹏等[4]提出了利用并列选择遗传算法提高定位精度,毛广玮等[5]利用模拟退火算法提高定位精度.然而，针对模型本身的构建误差研究尚无相关文献，而基于正确的模型所做的后续优化算法等研究才是有意义的. 本文基于模型本身的构建，进行误差分析，以减小模型的定位误差.

在利用视频影长数据进行定位的研究上，何伟梁等[6]利用线性相机模型实现了视频数据定位.但是该论文仅着眼于视频数据的还原，对文中120帧图片数据的获取方法未有提及.在影长定位的实际应用中，手动测量视频数据是极不方便的，本文提出了影长数据的自动提取算法以及还原的模型，提高影长定位模型的实用性.

1 影长定位的反演模型

影子长度与角度的变化包含着许多地理位置和时间的信息，这些信息为我们确定出物体所处的位置和时间提供了依据[7].

在经纬度给定时，影子方位角以及高度角的变化公式为：

sinθ=sinφsinδ+cosφcosδcosα

(1)

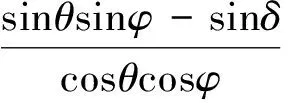
(2)

式中θ为太阳高度角，ω为太阳方位角，δ为太阳赤纬角，φ为纬度，α为太阳时角.α和δ的计算中包含经度和日期值，其详细计算可见文献[8].

在杆长H、日期已知的条件下，可以计算出杆的影长.

(3)

在已知影长数据及杆长、日期时，可以通过公式(1)、(2)进行反演求取经纬度，利用影长误差平方和最小建立如下的优化模型.

min∑(l′-l)2

(4)

s.t. |φ|≤90,|ψ|≤180,θi>0

(5)

式中l′为通过公式计算的理论影长，l为实际测量的影长，φ和ψ分别为纬度和经度.

该模型是非线性优化问题，可以用Matlab或lingo中带约束条件的优化命令求解，也可以用牛顿法、拟牛顿法求解，还可用遗传算法、粒子群算法等智能算法求解.本文借助R软件中的全局优化GenSA包利用模拟退火算法进行求解[9].若杆长未知，则可以利用相邻影长变化的相对值代替绝对值，改变优化目标，即

(6)

若日期未知，将日期做为离散值，分别得到每一天的最优解及相应的优化变量值，然后在得到的365个最优值中选取最优解，或者增加日期作为连续的优化参数，若日期求解结果不为整数，则分别对其进行向下取整和向上取整，选取最优值.

2 影长定位的误差分析

在反演模型中，影响定位精度的误差来源主要有两方面，一是物体影长的测量误差，二是优化模型的模型误差.前者主要为测量数据中的随机误差，后者则包括计算精度、优化算法的系统误差以及模型建立不当导致的人为误差.本文中主要研究测量的随机误差以及模型建立不当对定位精度造成的影响.

在影长定位的误差分析中，所采用的数据皆为仿真数据，即利用影长公式结合研究目的进行系统误差的设计得到模拟数据，利用模拟数据反演经纬度与实际经纬度进行比较分析，分析的方法主要为统计检验以及可视化比较.

2.1 影长测量误差对定位误差的影响

影响测量精度的因素有很多，由中心极限定理，测量的随机误差服从均值为0的正态分布，测量误差的偏倚由随机误差的方差反映，在测量绝对误差限确定时，可由公式(7)、(8)得到随机误差项方差的估计.

(7)

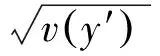
(8)

式中d为绝对误差限，Zα/2为标准正态分布的α/2分位数.

进而利用不同方差的正态分布随机数构造不同测量误差的仿真数据，并通过求解模型(4)式得到对经纬度的拟合结果.在同一地点，不同测量方差对物体影长定位的误差影响如图1所示.

图1 定位误差与测量误差关系图Fig.1 Quadratic relationship between positioning error and measurement error

从图中拟合二次曲线的系数，可以看出经度误差平方随测量方差增大幅度约为纬度误差平方的两倍.测量绝对误差限增长到10cm时，纬度偏误将达到0.28度，经度偏误达到0.39度.

2.2 大气折射对定位结果的影响

大气折射会造成影长测量数据与理论数据间存在定向的偏差.设太阳的入射角为π/2-θ，大气的折射率为n，折射角为π/2-θ′，由折射公式可得太阳高度角的余弦值为

(9)

在大气折射率已知的情况下，可由折射率公式计算出大气折射下的影长模拟值，进而用模拟值反演经纬度，并与未考虑大气折射的模型进行比较.由于大气折射率受温度湿度影响，其数值并非不变，在大气折射率未知的情况下，依然可仿真数据进行三参数(经纬度、大气折射率)的拟合与误差分析. 对一系列位置数据，分别用未考虑大气折射、考虑到大气折射(大气折射率未知)以及考虑到大气折射(大气折射率已知)的模型进行拟合，并对其结果进行成对样本T检验，其检验结果见表1.

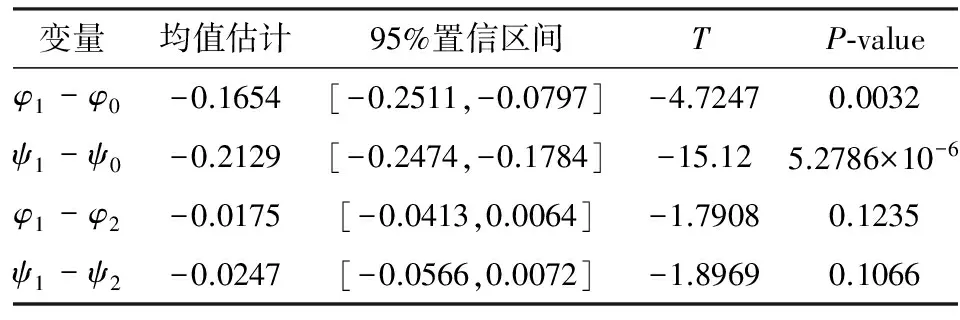
表1 大气折射对定位影响的T检验结果
Tab.1 The result of T-test on atmospheric refraction′s impact on positioning

变量均值估计95%置信区间TP⁃valueφ1-φ0-0．1654[-0．2511，-0．0797]-4．72470．0032ψ1-ψ0-0．2129[-0．2474，-0．1784]-15．125．2786×10-6φ1-φ2-0．0175[-0．0413，0．0064]-1．79080．1235ψ1-ψ2-0．0247[-0．0566，0．0072]-1．89690．1066

注:φ1考虑大气折射且折射率已知求解的纬度；φ0未考虑大气折射求解的纬度；φ2考虑大气折射且折射率未知求解的纬度；ψ1考虑大气折射且折射率已知求解的经度；ψ0未考虑大气折射求解的经度；ψ2考虑大气折射且折射率未知求解的经度;*95%置信水平下显著.

由检验结果可以发现，未考虑大气折射的模型与实际考虑大气折射的模型求解结果在纬度和经度上都有显著差异，而在大气折射未知时增加参数进行拟合对求解结果影响并不显著.因此，在实际进行反演定位时，应当考虑大气折射的存在，确定其值或设为未知参数代入影长定位模型.

2.3 地球椭球体模型下的影长定位

影长公式(1)、(2)的建立是基于地球正球体假设，而实际上地球是个不规则的椭球体.以地球中心为原点，赤道平面为x-y平面，指向北极的方向为z轴正向，固定某地P纬度为φ，正午时刻该地所在大圆的平面为x-z平面，建立如图2所示的坐标系，则P点在时角为α时的坐标为

R为赤道椭圆面的长轴半径，e为第一偏心率.则其切平面的法向量为

太阳入射方向的向量为

m=(-cosδ,0,-sinδ)

则椭球体模型中太阳高度角的变化公式为

(10)

图2 地球椭球坐标系Fig.2 Geographic coordinate system with Earth as an ellipsoid

在WGS-84坐标系中e2=0.006694379995，代入优化模型，利用修正后的椭球模型的模拟数据进行拟合，并对原模型结果与椭球体模型结果进行T检验，检验结果见表2.

表2 地球椭球模型对定位影响的T检验结果
Tab.2 The result of T-test on the impact of Earth shape on positioning

变量均值估计95%置信区间TP-valueφ1-φ00．1854[0．1780，0．1915]67．19407．308×10-10ψ1-ψ08．418×10-10[-8．3232×10-10，2．5159×10-9]1．23040．2646φ1-φ-0．0043[-0．0175，0．0088]-0．81010．4488ψ1-ψ-0．0018[-0．0109，0．0073]-0．47670．6504

注:φ1椭球模型求解的纬度；φ0未考虑椭球体求解的纬度；φ实际的纬度；ψ1椭球模型求解的经度；ψ0:未考虑椭球体求解的经度；ψ实际的经度;*95%置信水平下显著.

对椭球体考虑与否的模型求解结果在纬度拟合上有显著差异，故地球椭球体模型在进行定位反演时不可忽略.

2.4 误差分析结论

通过控制测量误差可以有效地提高定位的精度，而不可控的大气折射与地球形状引起的误差可通过模型修正规避.因此利用影长定位，在测量条件控制得当的条件下，可以实现较高精度，具有实用性.

而利用视频数据还原影长并定位，可以得到足够大的样本以减小测量方差，因此可以通过提高数据还原精度，控制影长定位的误差.

3 视频数据的反演模型

3.1 视频数据的提取

在对运动目标进行检测时，帧间差分法是常用的方法，但由于定位模型中使用的数据多为有一定时间间隔的离散序列数据，因此使用逐帧差分或三帧差分，都会造成巨大的计算量，且在只有序列图像数据时并不可用.因此结合三帧差分，提出了离散帧的三帧差分.

对于序列图像1，…，n,取第i(i

首先读取灰度图，得到像素矩阵M1,M2,M3；

然后分别用M2,M3对M1做差分，设定阈值T，进行二值化处理

(11)

接着对差分0-1矩阵做掩膜运算

(12)

同样的，对于i>n/2，取第i(i>n/2)张图片为pic1，第i-n/4张图片为pic2,第i-n/2张图片为pic3.使用相同的方法进行计算取得图像矩阵.计算得到的矩阵B，即为影子图像矩阵.应用该方法得到的提取效果如图3所示.

图3 影长图像提取Fig.3 Shadow image extraction

在图像数据时间间隔较小，或者影子变化不显著时，可以适当增大取帧步长，或是减小pic2的阈值.

提取出影长图像后，可以先进行闭运算再进行开运算以剔除数值为1的离群噪声点，然后求取图像中数值为1的点到杆底像素点的距离的最大值，即为图像中的影长.

经过实验，该自动提取算法具有较好的精度，其测量的影子长度与手动测量的结果相对误差小于0.25%.

3.2 视频数据的反演

视频数据是经过透视变换的，不能仅利用大小固定的比例进行还原，需建立三维空间坐标系(图4)进行透视还原.

图4 三维透视坐标系Fig.4 Three- dimensional perspective coordinate system

以直杆底端L(0,0,0)为原点，地平面为x-y平面，向东方向为x轴正向，向北方向为y轴正向，垂直向上方向为z轴正向建立直角坐标系.M(0,0,H)为杆子顶部，O(g,h,i)为摄像机光心,N(0,0,i)为杆上与光心等高的点,P(x,y,z)为影子的端点，P′、M′ 、N′、L′ 等分别为对应的成像后的点.

L点坐标为(0,0,0)，杆长为H，则M(0,0,H),O点坐标已知为(g,h,i)，则N(0,0,i).

(13)

故N′坐标为(a,b,i).

(14)

同理可得M′与L′坐标分别为(a,b,(1/k+1)i)、(a,b,i+(i-H)/k).又有NO与像平面垂直，可得像平面方程为

(15)

而P、O、P’三点共线，其直线方程为

(16)

联立上述两个方程，可解得P′(x′,y′,z′)为

(17)

(18)

(19)

若P与L处于同一水平面，则z=0(若P处于一倾斜平面，可联立PM直线与所在平面方程求解),

(20)

因此像平面中影长为|P′M′|

(21)

将理论值的l′与实际测得的图上影长构造误差平方和作为优化目标，建立形同式(4)-(5)的优化模型.若k值未知，可以利用式(6)消去k.除了使用计算图上影长的方法，也可以利用图像中影子端点坐标对实际影长进行还原，构建优化模型.经实验，在所需透视模型参数数据已知的情况下，视频数据定位具有较高的精度.

[1]马玉雪,令狐林玉,杨东海,等. 基于二次函数拟合的太阳影子定位技术研究[J]. 运城学院学报,2015(06):24-28.

[2]於炜力,窦如凤. 基于数学建模的太阳影子定位技术的研究[J]. 通讯世界,2016(18):270-271.

[3]胡毅华,杨旭龙,刘媛萍. 太阳影子定位模型的构建[J]. 洛阳师范学院学报,2015(11):13-18.

[4]于鹏,刘泽锋,郭改慧,等. 基于并列选择遗传算法的太阳影子定位方法[J]. 陕西科技大学学报(自然科学版),2017(1):193-197.

[5]毛广玮,袁洋,吴涵旭,文学. 基于模拟退火算法利用太阳影长估计经纬度的方法[J]. 科技展望,2016(15):139.

[6]何伟梁,凡皓,常钦皓. 基于极值优化的日影定位技术研究[J]. 南通职业大学学报,2016(4):63-66.

[7]蔡志杰. 太阳影子定位[J]. 数学建模及其应用,2015(4):25-33.

[8]于贺军. 气象用太阳赤纬和时差计算方法研究[J]. 气象水文海洋仪器,2006(3):50-53.

[9] MULLEN K M. Continuous global optimization in R [J]. Journal of Statistical Software, 2014, 60(6): 1-45.