一类光滑罚算法的全局收敛性

梁卓华(山东理工大学 数学与统计学院，山东 淄博 255049)

1 光滑罚函数

考虑约束优化问题

s.t.fi(x)≤0,0≤i≤m,

其中，fi:Rn→R(0≤i≤m)是连续可微函数， Ω0={x∈Rn|fi(x)≤0,1≤i≤m}≠φ．

不失一般性，假设

(1)

否则，可用ef0(x)来代替f0(x)．

非线性规划问题在科学管理，工程和经济管理等方面有广泛的应用．罚函数方法是解决非线性规划问题的重要方法，其主要思想是对目标函数增加惩罚项，将原问题转化为无约束优化问题．对于罚函数的研究已有很多文章[1-5]．

问题(CP)的l1精确罚函数为

(2)

文献[6]中给出的光滑罚算法是基于如下形式

(3)

式中：r是一个参数；θ(·)是一类光滑凸函数．随后Wang等[8]将式(3) 中的参数β进行了改进，给出了如下光滑罚函数

(4)

本文将式(4)进行推广，给出如下形式的光滑函数

(5)

这里的f(x)=(f1(x),f2(x),…,fm(x))，σ函数是满足第2节中,A1,A2,A3的函数，然后由罚函数(5)给出了一类光滑罚算法，并证明了一个摄动定理，由此摄动定理推出了罚算法的全局收敛性．

2 罚算法及全局收敛性

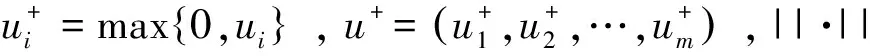
设函数σ∶Rm→R满足如下假设：

(A1) 对∀ε>0，∃ηε>0，使得

(A2) 对ck→+(k→)，存在εk→0+(k→)，有

(A3) 存在常数σ0使得

σ(u)≥σ0,∀u∈Rm．

容易验证函数σ(u)=||u+||α(α≥1)及σ(u)=||u+||2-||u+||均满足假设(A1)～(A3)．

命题1若假设(A2)成立，则存在σ1，对∀u≤0，都有σ(u)≤σ1．

证明由假设(A2)知，一定存在δ>0与k0使得

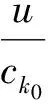
证毕．

对于问题(CP)给出新的罚函数

其中f(x)=(f1(x),f2(x),…,fm(x))．进一步给出基于L(x,β,r)给出一种罚算法并证明了一个摄动定理，由此摄动定理得到该算法的全局收敛性．

算法1

step0β0=1,r0=1,ω0=1，令k:=0．

step1 判定

(6)

否则，求非精确解xk满足

(7)

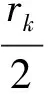
注 由(1)与假设(A3)，对∀β>0及r>0有

因此不论式(6)是否成立，满足式(7)式的全局非精确解总是存在的，即算法总是可行的，文献[8]给出的算法，在某些情况下是不可行的，这体现了本文结果的运用具有更加广泛性．

下面研究算法的收敛性．

对于ε≥0，定义问题(CP)的松弛可行集

Ωε={x∈Rn|fi(x)≤ε,1≤i≤m}．

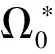
定义问题(CP)的摄动函数为

则问题(CP)的最优值为

设

Fε={x∈Rn|f0(x)≤θf0(ε)+ε}．

引理1算法产生的序列{rk}收敛于0．

=

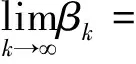
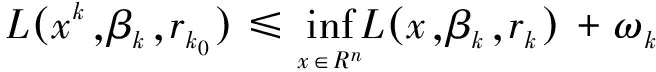
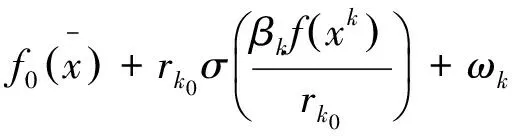
(8)

对于任意充分大的k≥k0，由假设(A1)有

≥

引理2∀ε>0，存在K，当k>K时都有Sk(ε)⊆Ωε．

证明用反证法．否则∃ε0>0及无穷子列K⊂N={1,2,…}使得∀k∈K，存在zk∈Sk(ε0)，zk∉Ωε0因此存在无穷子列K0⊂K，使得∀k∈K0与指标i0∈{1,2,…,m}，有

fi0(zk)>ε0

(9)

则由引理1及式(9)知，对充分大的k，||f+(xk)||>ε0≥rk．

由式(9)与假设(A1)，当k充分大时，有

(10)

又由step2知βk→+(k→)，因此(10)式右端趋向于正无穷．

(11)

(11)式左端是有界的，这样(10)式与(11)式矛盾．证毕．

定理1(摄动定理) 设{xk}是由算法所产生的点列，则有

(12)

再取δk>0且δk→0(k→)．根据下确界的定义，对每个k，存在使得

(13)

同时由于

因此得

(14)

另一方面，对∀ε>0，由引理2的证明过程知，对所有充分大的k，有

xk∈Ωε

(15)

从而，对∀ε>0，由假设及(13)-(14)，有

θf0(ε)≤f0(xk)≤

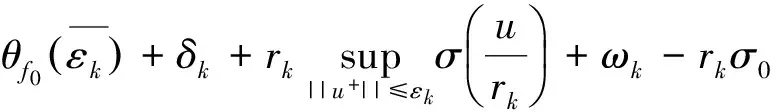
令k→，于上式两端取极限，由式(12)即得．证毕．

由此定理可以得到下面推论．

推论1设{xk}是由算法所产生的点列，则它的每一个聚点都是问题(CP)的最优解．

证明由引理2，对充分大的k有

xk∈Ωε

(16)

设x*是序列{xk}的一个聚点，由fi(0≤i≤m)的连续性及式(16)即知x*∈Ωε．再据ε>0的任意性知，x*∈Ω0．

由摄动定理，有

证毕．

3 结束语

罚函数与精确罚函数在多个领域应用很广泛，并且起着非常重要的作用，多年来，很多学者对罚函数进行了深入研究．本文给出了一种光滑罚算法并证明了其全局收敛性．这为求解约束规划问题，提供了一个新的方法．

[1]LIU J, TEO K L, WANG X. An exact penalty function-based differential search algorithm for constrained global optimization[J]. Soft computing, 2016, 20(4): 1 305-1 313.

[2] ZHOU J, LOVE P E D, TEO K L. An exact penalty function method for optimising QAP for mulation in facility layout problem[J]. International Journal of Production Research, 2016: 55(10):2 913-2 929.

[3]GONZAGA C C,CASTILLO R A. A nonlinear programming algorithm based on non-coercive penalty functions[J].Mathematical Programming, 2003, 96(1):87-101．

[4] BOLAND N L, EBERHARD A C. On the augmented lagrangian dual for integer programming[J] . Mathematical Programming , 2015,150(2):491-509．

[5] BURACHIK R S, IUSEM A N, MELO J G. The exact penalty map for nonsmooth and nonconvex optimization[J]．Optimization,2015,64(4), 717-738．

[6] WANG C Y. Global convergence and finite termination of a class of smooth penalty function algorithms[J]. Optimization Methods & Software, 2013, 28(1):1-25．

[7] WU Z Y, BAI F S, LEE H W J. Quadratic smoothing approximation to exact penalty function in global optimazation [J]. Journal of Industrial & Management Optimization, 2005, 1(4):533-547．

[8] WANG C, MA C, ZHOU J. A new class of exact penalty functions and penalty algorithms[J]. Journal of Global Optimization, 2014, 58(1):51-73．

[9] WU Z Y, BAI F S,YANG X Q. An exact lower order penalty function and its smoothing in nonlinear programming[J]. Optimization, 2004, 53(1):51-68．

[10] BEN-TAL A, TEBOULLE M. A smoothing technique for nondifferentiable optimization problems[M]. Optimization Springer Berlin Heidelberg, 1989:1-11．

[11] HUANG X X, YANG X Q. A unified augmented lagrangian approach to duality and exact penalization[J]. Mathematics of Operations Research, 2003, 28(3):533-552．