介质折射率对矩形波导有效折射率的影响
潘继环, 张元文
(河池学院 物理与机电工程学院, 广西 宜州 546300)
介质折射率对矩形波导有效折射率的影响
潘继环, 张元文
(河池学院物理与机电工程学院, 广西宜州546300)
基于电磁波动理论,通过马卡梯里法近似求解矩形波导模式特征方程,研究介质折射率对矩形波导有效折射率的影响。结果表明:无论模阶数取何值,矩形波导有效折射率随芯层折射率的增大而增大,随包层折射率的增大而减小;当芯层与包层折射率比保持不变时,随介质折射率的增大而增大;当孔径数值变大到某一数值,有效折射率均出现简并现象。这些影响规律对矩形波导的实际应用具有一定的理论指导意义。
矩形波导;马卡梯里法;介质折射率;有效折射率
矩形波导是集成光学应用的重要器件,是由截面形状为矩形的金属材料(铜、铝等)构成、内部填充空气介质的金属波导[1-5]。目前对波导的应用,虽然在低频段和高频段面临一些困难,但因其具有损耗低、电磁屏蔽性能好等优点,在军事、民用等大功率情况下的作用是无可取代的,如在通信传输线平面集成化、小型化等方面具有广泛的应用[3-13],自从汤姆逊在1936年成功预言波导以来,波导就一直成为各国科学家们最热门的研究课题之一。
对于平板波导和矩形波导的研究,相关文献报道比较多,但对矩形波导有关介质折射率的研究还是比较少见。在矩形波导的各个参数中,传播常数是最重要的参数之一,它对光波导及其所构成的光器件的设计都起着指导性的作用[3-14]。而传播常数的计算方法之一便是由矩形波导的有效折射率来计算,因而研究影响矩形波导有效折射率的因素就显得尤为重要。因此,本文通过研究介质折射率对矩形波导有效折射率的影响,并分析和总结出它的规律,力求得到比较精确的有效折射率,从而为获取较为精准传播常数的计算提供参考。
1 模型及计算方法
1.1矩形波导结构
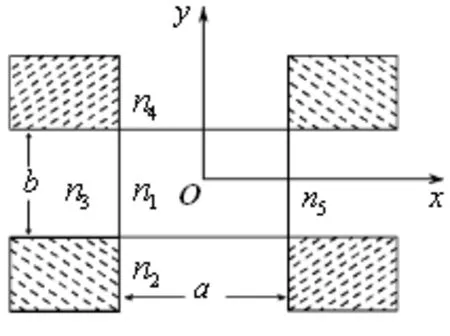
图1 矩形波导横截面图
假设矩形波导结构的截面如图1所示,将各波导层划分为9个区域(3*3),中间为矩形波导芯层简称芯层,令芯层的折射率为n1,长度和宽度分别为a、b,紧邻芯层周围分别为波导包层(即四个白色区域)和四个角区(即四个阴影区域),其中令包层的折射率n2=n3=n4=n5。由于光在阴影区传播的功率相对较弱,在具体分析问题时可作近似忽略,并以芯层的中心为坐标原点建立直角坐标系,Z轴垂直于纸面向里。
研究方法采用马卡梯里法[4-6,11],该方法主要是把矩形波导中间竖着的三个区域看作水平的平板光波导,中间横着的三个区域看作竖直的平板光波导,因此用平板光波导的理论就可以很方便的求出矩形光波导所需的参数。
1.2理论公式推导
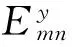
(1)
2 介质层折射率对有效折射率的影响
2.1芯层折射率n1对有效折射率Nx的影响
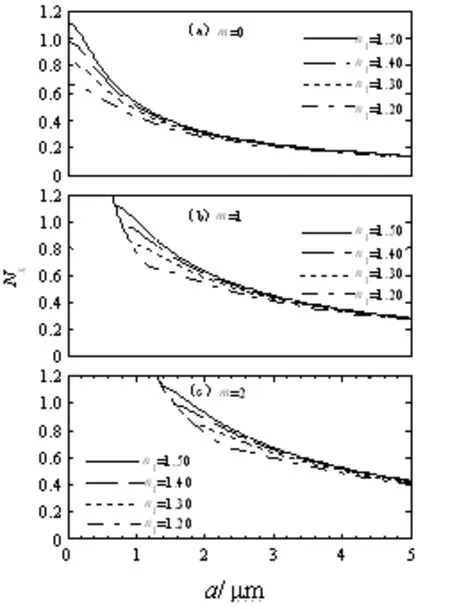
图2 芯层折射率变化与有效折射率Nx的关系
为研究芯层折射率对有效折射率的影响,分别取参数λ0=1.55 μm,包层折射率n2=n3=n4=n5= 1.20,模阶数取m=0~2,当芯层的折射率n1分别取值为1.20、1.30、1.40、1.50时,对方程(3)利用Matlab编程模拟绘制出芯层折射率n1与有效折射率Nx的关系,如图2所示。
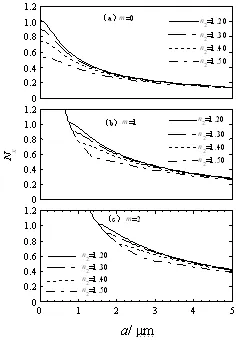
图3 包层折射率变化与有效折射率Nx的关系
从图2中可以看出:(1)无论模阶数取何值,当芯层折射率n1从1.20~1.50发生变化时,有效折射率都是随着芯层折射率的增大而增大,同时x轴孔径越大矩形波导的有效折射率越容易趋于简并。(2)在图2(a)中,对于基模(即m=0),无论芯层折射率如何变化,有效折射率都小于1.20,并且在芯层宽度0~5 μm范围,有效折射率均衰减至0.14,开始出现简并现象,而光能在芯层中传播的条件是有效折射率介于n1和n2之间,即1.20 另外,矩形波导在x轴上支持模阶数m≥1的多模传输,但要求数值孔径不能太大,如果太大了矩形波导就容易变成了表面模。经过计算得知,孔径大小维持在0~8 μm范围比较合适。 2.2包层折射率n2对有效折射率Nx的影响 同样取参数λ0=1.55 μm,芯层折射率n1=1.50,模阶数分别为m=0、1、2,当包层的折射率n2=n3=n4=n5分别取值1.20、1.30、1.40、1.50时,对方程(4)利用Matlab编程模拟,绘制出包层折射率n2与有效折射率Nx的关系,如图3所示。 图4 介质折射率比值对有效折射率Nx的影响 从图3中可知:(1)无论模阶数取何值,当包层折射率n2分别取值为1.20、1.30、1.40、1.50时,有效折射率均随着包层折射率的增大而减小,同时孔径数值越大,有效折射率就越容易趋于简并。(2)在图3(a)中,对于基模(即m=0),不管包层折射率如何变化,有效折射率均小于1.10,在芯层宽度0~5 μm范围内,衰减至0.12,开始出现简并现象。(3)在图3(b)、(c)中,有效折射率均大于1.20,无论芯层折射率如何变化,当m=1时有效折射率衰减至0.35,开始出现简并现象;当m=2时有效折射率衰减至0.42,开始出现简并现象,以此类推,模阶数越大,就越容易出现简并现象。 因此,要提高波导的有效折射率,就要增大芯层介质的折射率,相反地,如要减小波导的有效折射率可增大包层介质的折射率。 2.3介质折射率比n1/ n2对有效折射率Nx的影响 同样地,取λ0=1.55 μm、包层折射率n2=n3=n4=n5不变,当模阶数取m=0、1、2时,介质折射率比(即芯层与包层折射率比)固定为n1/n2=1.20,即n1分别取1.68、1.56、1.44、1.32,则对应的n2分别为1.40、1.30、1.20、1.10,对方程(3)、(4)利用计算机模拟绘制出介质折射率比n1/n2与有效折射率Nx的关系,如图4所示。 从图4中可以看出,当比值n1/n2为1.20不变时,有效折射率Nx同时随着芯层和包层介质折射率增大而增大。在芯层宽度0~5 μm范围内,当m=0时,有效折射率均小于1.0,且衰减至0.15,开始出现简并现象,如图4(a)所示;当m=1时,有效折射率衰减至0.28,开始出现简并现象,如图4(b)所示;当m=2时有效折射率衰减至0.42,开始出现简并现象,如图4(c)所示。 综上所述,介质折射率的变化对矩形波导的有效折射率有调制作用。另外,笔者阅读一些相关文献报道,了解到用矩形波导有效折射率法来计算传播常数,得到的结果偏差稍大。因此,利用介质折射率变化对矩形波导有效折射率的调制作用,可以减小因用有效折射率法来进行计算传播常数而出现误差偏大的问题。 采用马卡梯里法研究了介质折射率对矩形波导有效折射率的影响,得出以下结论: (1)无论模阶数取何值,矩形波导有效折射率随着芯层折射率的增大而增大,随着包层折射率的增大而减小;当芯层与包层折射率比保持不变时,随着介质折射率的增大而增大。 (2)随着芯层孔径数值的增大,有效折射率均出现简并现象。 介质折射率对矩形波导有效折射率的影响规律,可为以矩形光波导器件为理论基础的集成光学器件、光电子器件提供一定的理论指导,也为减小因用有效折射率法来进行计算传播常数而出现的误差提供了参考。 [1]孙杰,杨剑锋,闫肃,等.等离子体辅助平板波导的传输特性及应用研究[J].物理学报,2015,64(7):078402. [2]佘守宪.导波光学物理基础[M].北京:北方交通大学出版社,2002:124-152. [3]马春生,刘式墉.光波导模式理论[M].长春:吉林大学出版社,2006:172-203. [4]蒙成举,卢强华,欧梅莲,等.单负材料填充包层的矩形波导模式特性[J].广西科学,2015,22(1):94-98. [5]吴美燕,罗砚浓,欧梅莲,等.含左手材料四层平板波导的模式特性[J].广西科学,2015,22(1):99-103. [6]潘继环,张元文. 芯层宽度对矩形波导有效折射率的影响[J].河池学院学报,2015,35(5):46-49. [7]唐裕霞,罗成,彭家华.分别含左右手材料的三层平板波导中光导模的比较研究[J].重庆工商大学学报(自然科学版),2014,31(7):63-69,76. [8]许江勇,段国华,张卫龙,等.Metal-LHM-Metal三层对称平板波导的传输特性研究[J].广西科学,2012,19(3):236-238. [9]潘继环,苏安,唐秀福, 等.缺陷奇偶性对光子晶体光传输特性的影响[J].激光与红外,2015,45(6):706-709. [10]张静,何英,李春芳,等.包含左手材料的四层平板波导中的光导模[J].光学学报,2009,29(10):2673-2680. [11]王振永,周骏,张玲芬,等. 左手介质矩形波导导模和表面模的场分布[J].光学学报,2008,28(8):1558-1564.. [12]诸一琦,陈宪锋,杨烨.特异材料对矩形波导导波模式的影响[J].常州工学院学报,2013,26(5):20-24. [13]韦吉爵,苏安,唐秀福,等. 缺陷对一维光子晶体滤波性能的调制[J].红外与激光工程,2015,44(S1):168-172. [14]苏安,蒙成举,高英俊.激活性杂质对光子晶体量子阱滤波器特性的调制[J].中国激光,2014,41(3):0306001. [责任编辑刘景平] Influence of Medium Refractive Index on the Effective Refractive Index in Rectangular Waveguide PAN Ji-huan, ZHANG Yuan-wen (School of Physics and Mechanical & Electronic Engineering, Hechi University,Yizhou, Guangxi 546300, China) The study uses Marca ladder in approximation theory and electromagnetic waves theory to solve characteristic equation of the rectangular waveguide mode, and research the influence of the refractive index on the effective refractive index in rectangular waveguide. The result shows that whatever the value of mode order is, the effective refractive index in rectangular waveguide increases with the increase of the core refractive index and decreases with the increase of the cladding refractive index; when the ratios of the core refractive index and the cladding refractive index remain constant, the number of the effective refractive index is increased with the increase of the refractive index of the medium; the curve of the effective refractive index begins to degenerate when the numerical aperture becomes large to a certain value. These laws can provide theoretical guide to study the practical application of a rectangular waveguide. rectangular waveguide; Marca ladder theory; effective refractive index; refractive index O431 A 1672-9021(2016)02-0039-04 潘继环(1972-),男,广西都安人,河池学院物理与机电工程学院副教授,主要研究方向:光子晶体。 广西高校科学技术研究基金资助项目(KY2015YB258);河池学院重点科研基金资助课题(2014ZD—N001);2015年自治区级大学生创新创业训练计划立项项目(201510605057)。 2016-03-07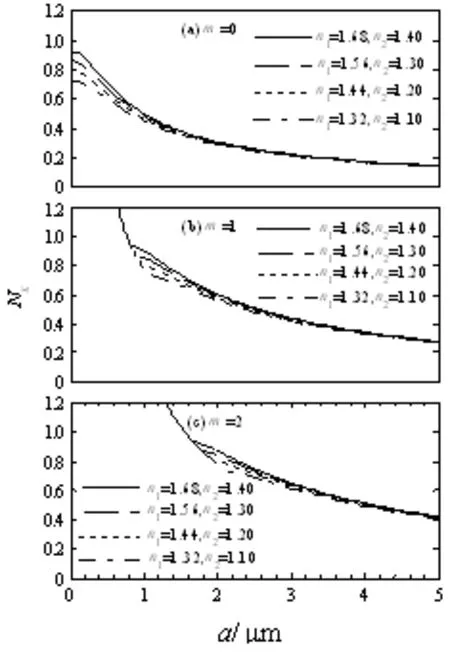
3 结论

