带有截缝的矩形波导内TEM波的场结构及其特性阻抗
王福谦
(长治学院 电子信息与物理系,山西 长治 046011)
带有截缝的矩形波导内TEM波的场结构及其特性阻抗
王福谦
(长治学院 电子信息与物理系,山西 长治 046011)
通过求解拉普拉斯方程,研究带有截缝的矩形波导内TEM波的场结构,利用软件HFSS进行结构仿真,绘制出该波导横截面及内部TEM波的场结构图,并计算其特性阻抗。
带有截缝的矩形波导;拉普拉斯方程;TEM波;HFSS;结构仿真;特性阻抗
矩形波导是横截面为矩形的金属波导管,关于该波导中TE10模的电磁场结构及传输特性,有关文献[1-2]中已作了论述。但对于带有截缝的矩形波导内的TEM波的场结构,相关文献还未见涉及。为此,文章拟通过解拉普拉斯方程来研究带有截缝的矩形波导内TEM波的场结构,利用软件HFSS对其进行结构仿真,并计算其特性阻抗。
1 带有截缝的矩形波导内静电场的级数解
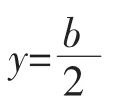
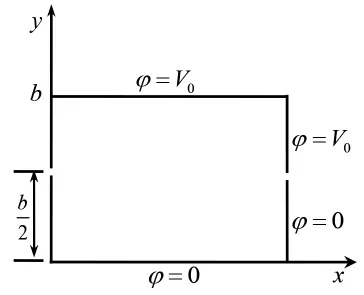
图1 带有截缝的矩形波导的横截面
当导体管的上半部保持为电位V0而下半部接地时,该波导管内的电势φ(x,y)满足拉普拉斯方程
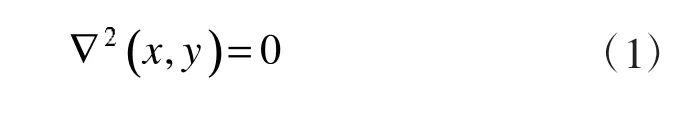
设其解为:
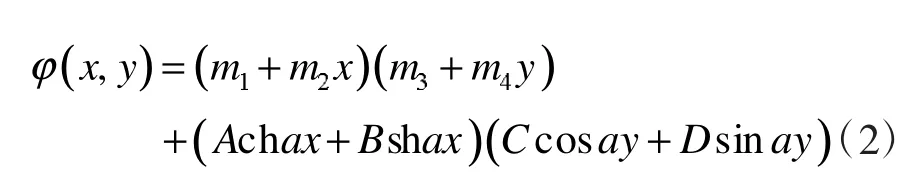
式(2)中的系数由下列边界条件确定:由边界条件y=0,φ=0,得C=0,m3=0,则式(2)可表示为:
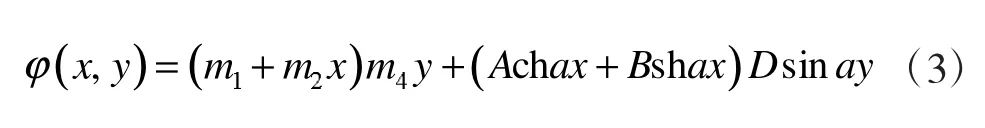
再由边界条件y=b,φ=0,式(3)可写为:
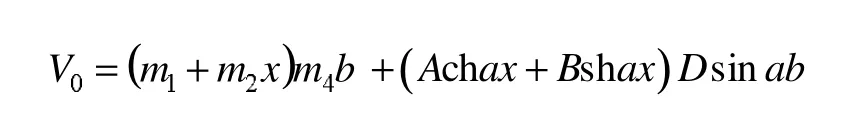
要使上式对x的一切值都成立,只有sinab=0,即ab=nπ,故有:
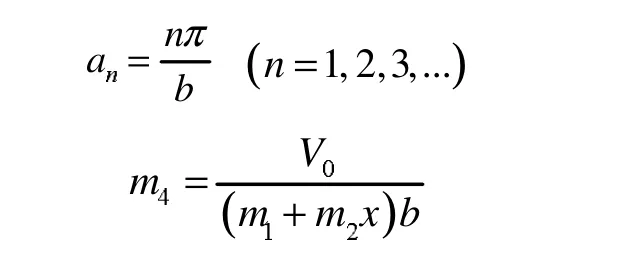
则式(3)变为:
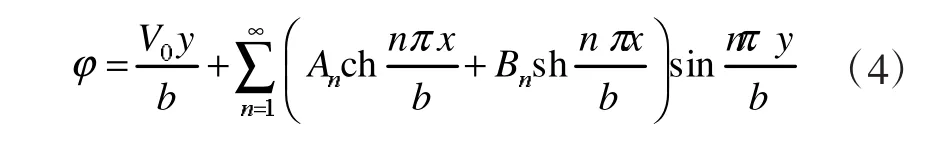
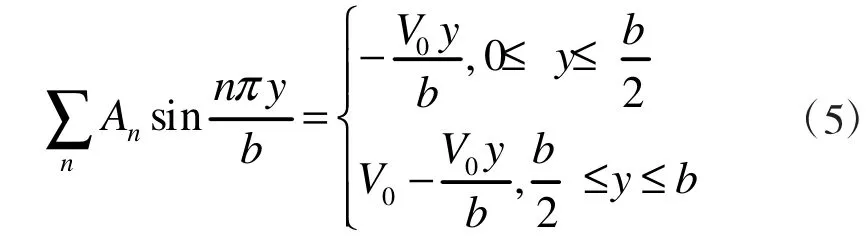
当x=a时,有:
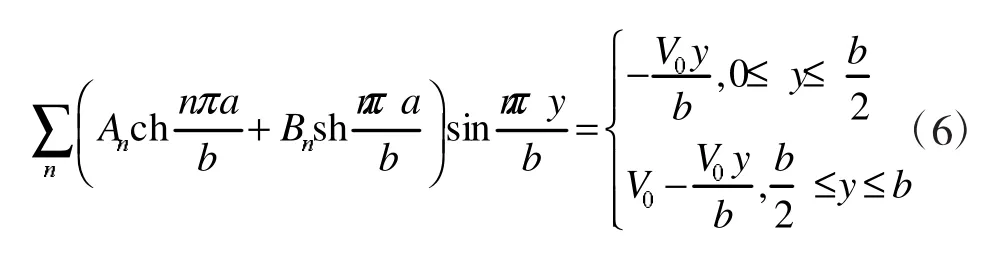
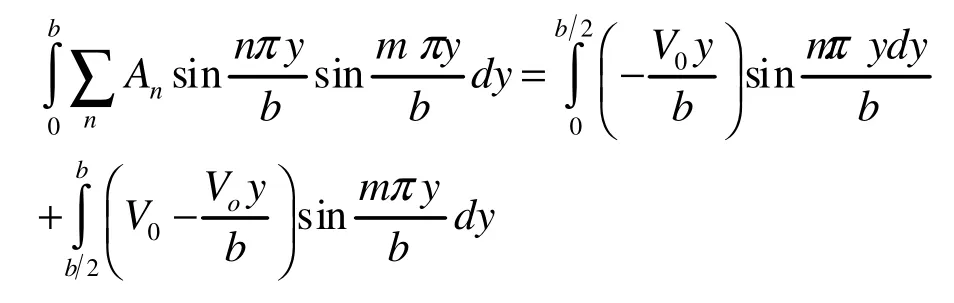
积分得:
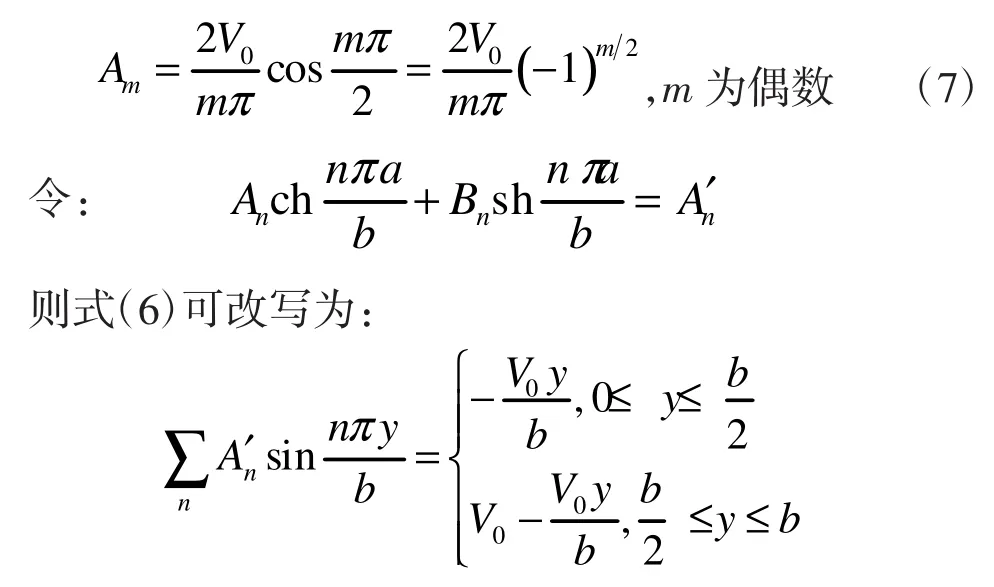
同理,得到:
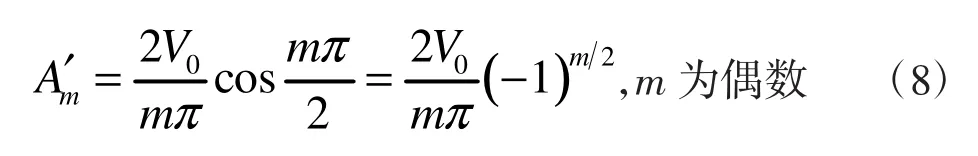
联立(7)、(8)两式,并将m改为n,可得:
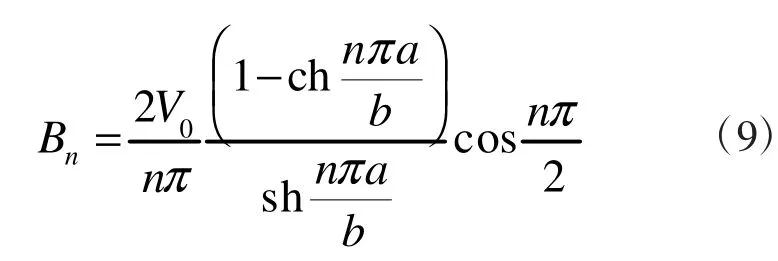
将An和Bn的结果代入式(4),得到带有截缝的矩形波导内的电势分布为:
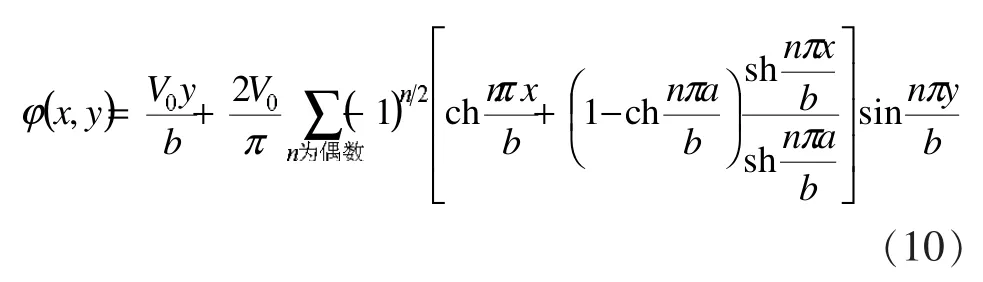
由场强与电势的微分关系E=-▽φ,利用式(10)得场强的矢量表达式为:
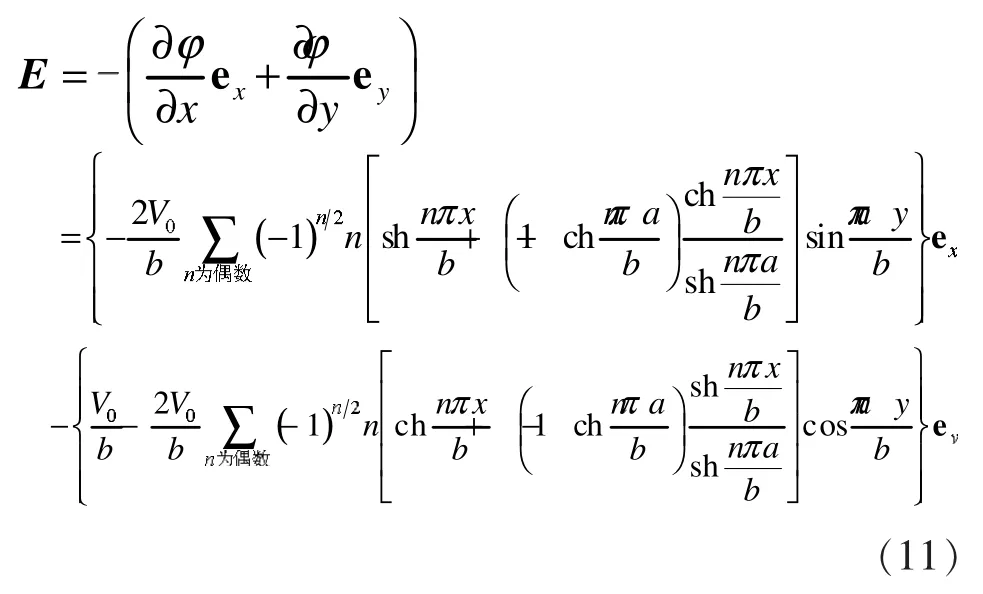
式(11)为在静态场情形下的带有截缝的矩形波导内的场强分布表达式。式中ex、ey为该沿波导横截面上沿x、y方向的单位矢。
2 带有截缝的矩形波导内TEM波的解析解
带有截缝的矩形波导内TEM波的求解,可由静态场在相同边界条件下的解,得到其电场在此波导横截面上的分布,乘以波动因子e-jβz得到电场的解,再由麦克斯韦方程组所给出的电、磁场关系得到其磁场的解[3]。则带有截缝的矩形波导中的TEM波的场强分布为:
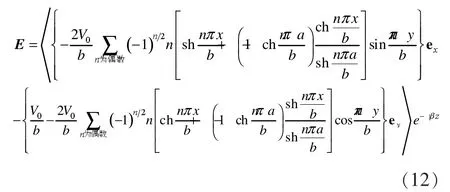
TEM波的电场与磁场相互联系,满足如下规律[3]:
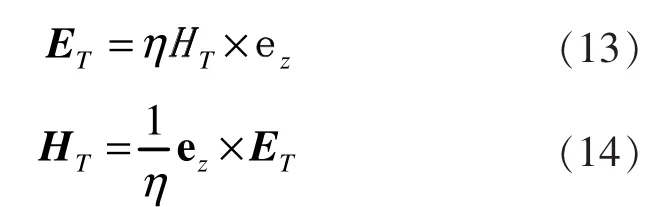
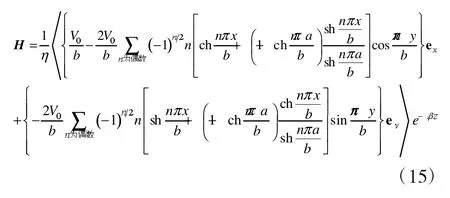
又由式(14)、(12),得:式(12)、(15)即为带有截缝的矩形波导内TEM波的解析解。这两个式子给出了带有截缝的矩形波导内TEM波的场结构。
3 TEM波的结构仿真
图3至图5为通过HFSS[4,5]软件仿真出的带有截缝的矩形波导内TEM波的三维电磁场结构图,场分布形象直观,便于对场结构的整体把握。该图也可供功率耦合及设计有源器件时使用和参考。
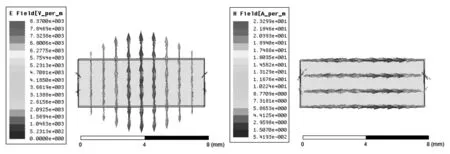
图3 带有截缝的矩形波导横截面上TEM模的场结构图(由HFSS软件仿真)

图4 带有截缝的矩形波导内TEM波的场结构图(由软件HFSS仿真,Field Overlays:Vector-E、Vector-H)

图5 带有截缝的圆波导内TEM波的场结构图(由软件HFSS仿真,Field Overlays:Mag-E、Mag-H)
4 特性阻抗
传输线的特性阻抗z0与单位长度电容C0的关系为[6]

式中,ε和μ为传输线内填充介质的介电常数和磁导率。
当中部带有截缝宽度为Δ的矩形波导内充满介电常数为ε的均匀介质时,其U型板单位长度上的带电量为:
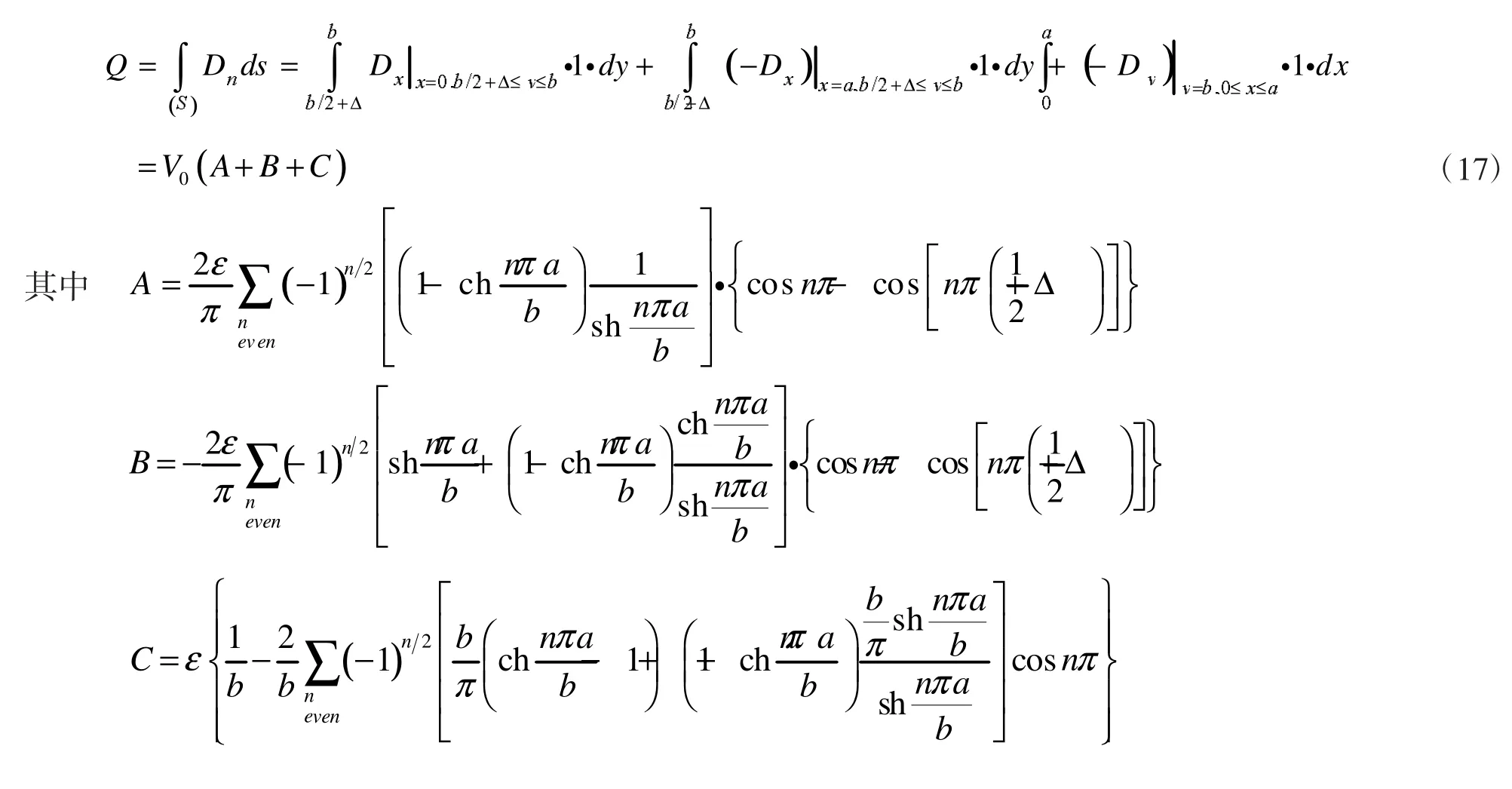
由式(17)可得带有截缝的矩形波导单位长度的电容量为:
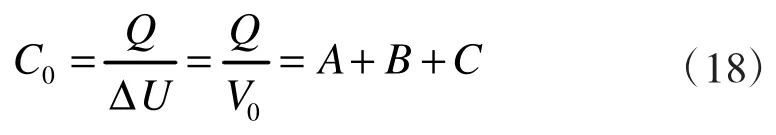
则带有截缝的矩形波导的特性阻抗为:
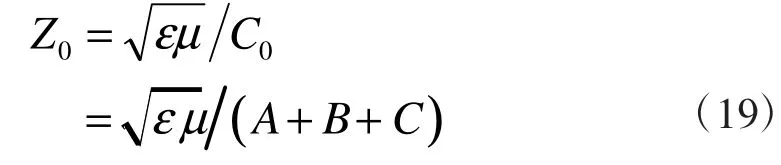
由式(19)可知,带有截缝的矩形波导的特性阻抗不但取决于波导的尺寸及截缝的宽度,而且还与其所充入电介质的电磁参量ε和μ有关。
5 结束语
文章将理论分析与计算机模拟相结合,研究了带有截缝的矩形波导内TEM波的场结构,给出了该波导内TEM波的解析解,对其场结构进行了仿真,并计算出其特性阻抗。对于波导内TEM波的场分布,了解其功率容量,计算衰减常数,考虑功率耦合及设计有关的有源器件等都是不可缺少的,故文章所得结论具有一定的理论意义和实践价值。
[1]谢处方,饶克谨.电磁场与电磁[M]北京:高等教育出版社,2006.264-278.
[2]符果行.电磁场与电磁波[M]北京:电子工业出版社,2009.190-199.
[3]沈熙宁.电磁场与电磁波[M].北京:科学出版社,2006.379-381.
[4]谢拥军,等.HFSS原理与工程应用[M].北京:科学出版社,2009.
[5]李明洋,等.HFSS天线设计[M].北京:电子工业出版社,2011.
[6]朱满座.数值保角变换及其在电磁理论中的应用[J/OL].(2008-12-01):http//www.cnki.net/kcms /detail/detail/aspx.93-98.
O44
A
1673-2014(2017)05-0001-04
山西省自然科学基金(2012011028-1)
2017—05—16
王福谦(1957— ),男,山西临猗人,教授,主要从事电磁场边值问题及场结构数值模拟研究。
(责任编辑 郝瑞宇)

