基于镜像选择序优化的MART算法
李志博,李清宝,兰明敬,孙剑帆
(中国人民解放军战略支援部队信息工程大学,河南郑州 450001)
1 引言
被测程序通常有较大的输入空间,因此选择一部分可以有效识别软件失效的测试输入作为测试数据具有重要意义. 测试数据生成技术指导如何生成高效的测试数据,如随机测试(RT)数据生成方法[1]、基于符号执行的测试数据生成方法[2]、基于有限状态机的测试数据生成方法[3]、基于智能搜索的测试数据生成方法[4,5]等. 文献[6]提出了一种基于变异分支优势度排序的弱变异测试数据生成方法,在提高了测试集的错误检测能力的同时提高了效率. 对于MPI 程序的路径覆盖测试,文献[7]提出了一种将集成代理模型(ESM)的估计集成到测试数据生成过程中的方法,以此来降低适应度值的计算量. 文献[8]提出了一种基于代理辅助进化优化的MPI 程序路径覆盖测试数据生成方法,该方法能有效地生成高质量的测试数据.
RT 是一种简单、易于实现的测试方法. 它不涉及到复杂的软件需求或程序的内部结构信息,只需在输入域内随机地生成测试数据即可.RT 没有利用被测软件的任何信息,且生成的测试数据具有冗余度高,覆盖度低,盲目性等缺点,曾被Myers 认为可能是最糟糕的测试方法. 但由于RT 具有简单、易实现、成本低、无偏性、速度快等优点,易与其它测试方法结合使用,因此被广泛应用在各个领域的软件测试和可靠性评估中.同时,所有测试方法生成的测试数据理论上均可由RT生成,因此RT具有发现一切错误的潜力[9].
经实验研究发现,引发失效的输入易于聚集在连续的区域. 依此结论,Chen 提出了ART(Adaptive Random Testing)算法[10]. 与RT 不利用任何信息随机产生测试数据相比,ART 算法利用已执行成功测试数据的信息,以及引发失效的输入易于集中的特征,使生成的测试数据尽可能均匀的分布在输入空间内. 实验表明ART 的检错有效性较RT 有明显改善,发现第一个错误所需的测试数据数量更少. 学术界提出了各种基于ART 思想的改进算法,例如,基于距离的ART 算法(DART)[11],基于限制的ART 算法(RRT)[12],基于划分的ART 算法[13]等. ART 也是一种基础测试方法,应用领域非常广泛,易于同其他测试数据生成方法结合,提升测试数据生成方法的有效性,如ART 与程序的路径覆盖信息相结合用来提升测试数据生成的有效性[14]、ART 用于安全测试生成检测XSS 漏洞的测试数据[15]、ART 与基于搜索的测试数据生成方法相结合,在蚁群算法的局部搜索中引入了ART[16]、ART 用于测试数据优先级排序,将FSCS 算法用于测试数据优先级排序,检错能力优于随机法与贪婪法[17]. 文献[18]在不同测试场景下对组合测试、RT、ART 进行了对比实验,实验结果显示ART 优于RT,并且在96%的测试场景下检错能力与组合测试相近.
但是ART 算法需要额外的开销使生成的测试数据更加均匀. 尤其是基于距离的ART 算法,距离计算是算法较大的开销,这些开销减少了ART 算法的可用性,降低了ART 算法生成测试数据的效率. 镜像策略是一种有效提高测试数据生成效率的手段. 通过镜像策略,将已生成测试数据通过镜像函数生成新的测试数据,减少了ART算法的计算开销,提高了ART算法的效率,但是降低了ART算法的有效性[19].
2 镜像策略
根据镜像策略在ART 算法中的实施流程划分,MART 算法主要包括三个部分:镜像划分、镜像函数和镜像选择序.
2.1 镜像划分
镜像划分指将输入空间划分子域的方式. 根据各维度划分是否均等,分为相等划分和非等划分.
假设N为输入空间D的维度数量,即|D| =N,每个维度用Xi(i=1,2,3,…,N)表示,将维度Xi平均划分的数量用ki(i=1,2,…,N)表示. 若对输入空间D进行镜像划分后,存在两个维度Xi与Xj划分的数量不等,即ki≠kj,称为非等划分. 若对输入空间D进行镜像划分后,任意两个维度Xi与Xj划分的数量都相等,即ki=kj,称为相等划分.
在相等划分中,若每个维度划分后的个数ki(i=1,2,…,N)可以用2ω(ω=1,2,3,…)表示,如
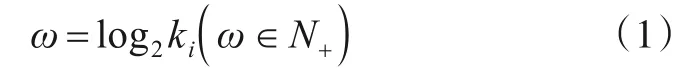
称此类相等划分为对等划分,ω为镜像划分的深度,子域数量m=(2ω)N.
2.2 镜像函数
通过镜像划分方法,将输入空间划分为m个子域.选择其中一个子域作为源域,源域中应用ART 算法生成测试数据,其余m-1 个镜像子域中如何对应生成测试数据,则是通过镜像函数将源域中的测试数据映像到镜像域中.
常见的镜像函数有平移和对称.
假设在n维输入空间中,源域空间为D0,镜像子域为Dk,其中,
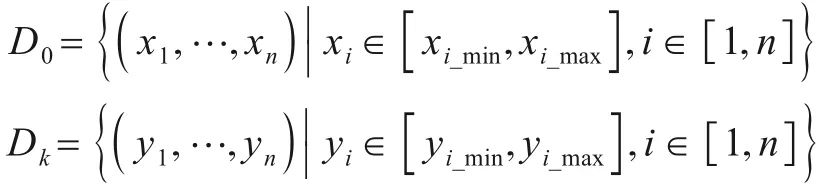
在源域空间D0中,测试数据生成算法生成的测试数据为tc0=(t1,t2,…,tn),则测试数据tc0在镜像子域Dk中的镜像测试数据tck为:
(1)若镜像函数为平移,则:

(2)若镜像函数为对称,则:
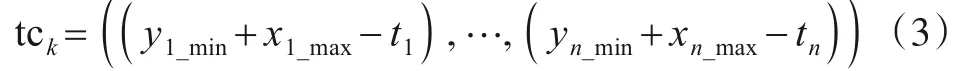
如图1所示,在2维输入空间中,镜像划分深度为1时,划分后的镜像子域的数量为4. 假设阴影部分子域作为源域,源域中通过算法生成测试数据,根据镜像函数将源域中的测试数据镜像到其余的各子域中,通过平移镜像函数生成镜像测试数据如图1(a)所示,通过对称镜像函数生成镜像测试数据如图1(b)所示.
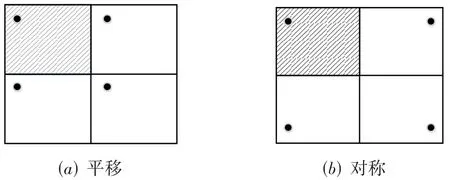
图1 两种镜像函数示意图
对称镜像函数可能出现如图2所示的情况,使测试数据在整个输入域中分布不够均匀.
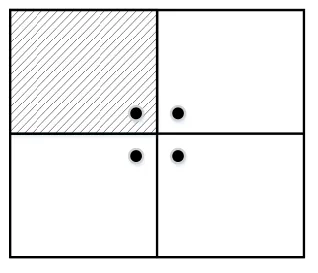
图2 对称镜像可能存在的问题
相对来说,平移镜像函数较对称镜像函数在镜像子域中生成测试数据更均匀.
2.3 镜像选择序
源域中的测试数据先执行,然后是镜像域中的测试数据. 当镜像子域的数量较多时,不同镜像子域内测试数据执行顺序对算法有效性也有影响.
镜像选择序是不同镜像域中的测试数据执行顺序,有顺序选择序、随机选择序等.
顺序选择序指选择镜像域的顺序按从左到右、从上到下的固定顺序依次选择. 将2 维输入空间划n行m列,每个子域顺序编序,则选择镜像域的顺序即xi的下标序.
随机选择指随机在m·n-1 个镜像域中选择一个,根据镜像函数生成测试数据进行执行.
3 基于镜像策略的ART算法
基于镜像策略的ART 的思想[19]:将输入空间划分为多个不相交的相等子域,源域中使用ART 算法生成测试数据,剩余子域中使用镜像函数生成镜像测试数据. 详见算法1.

算法1 MART算法输入:输入域维度n,划分深度ω,失效域F随机分布在输入域中.输出:生成测试用例集E.1. 初始时,E=Ø;2. 根据镜像相等划分策略划分输入域,一共划分成2n·ω个子域;3. 任选一个子域D1作为源域;4. 在源域D1中依据ART算法生成一个测试用例tc;5. 如果tc检测到失效,转到步骤10;否则,将tc存入E中.6. 根据镜像域的选择序确定测试用例tc待镜像的下一个子域m;7. 根据镜像函数,计算出镜像子域m中的镜像测试数据tc';8. 判断tc'是否检测到失效,如果检测到失效转向步骤10;否则,将tc'存入E中.9. 若所有2n·ω-1镜像子域中已生成测试数据tc的镜像测试数据,则转向步骤4;否则,转向步骤6.10. 算法终止.
将输入域空间D等分为D1和D2两部分. 若取D1为源域,D2为镜像域,仅需在D1中使用ART 算法生成测试数据,通过镜像函数平移到D2中,使D1与D2中测试数据具有相同分布,而只在D1中进行了距离的计算. 假设输入域空间D等分为m个子域,若ART算法与MART 算法生成相同数量测试数据,MART 只需要ART距离计算的1/m2[20].
4 基于镜像选择序优化的MART算法
4.1 问题提出
镜像随机选择序是随机选择未生成镜像测试数据的镜像子域,生成镜像测试数据. 镜像域的随机选择序简单,易实现,一定程度上较均匀的选择镜像子域,从而生成的镜像数据过程也是随机的.
镜像随机选择序可能会出现已生成测试数据的子域与被选择镜像子域在某个维度下是属于同一个分区的情况,如图3所示.

图3 镜像随机选择序可能存在的问题
如图3所示,假设在二维输入空间中,镜像深度ω=2时,镜像划分后,输入空间被平均划分成16个子域,图中深色正方形区域为失效域. 选取标号“1”的域为源域,源域中生成测试数据后,选择镜像子域生成镜像测试数据,如果选择的镜像子域在阴影子域内,则无法触发缺陷,因为失效域在白色子域所在范围内. 镜像子域随机选择序是随机的选择子域,不做任何限制,可能会出现选择的镜像子域与已生成测试数据的子域在相同行或相同列的现象,也就是选择生成测试数据的镜像子域在某个维度或多个维度上取值范围相同.
针对镜像随机选择序可能出现的这种情况,考虑对镜像选择序进行约束,本文通过限制镜像子域选择序,增强镜像子域选择序的多样性,从而提高MART 算法的检错有效性.
4.2 镜像受限选择序
镜像受限选择序是每次选择镜像子域生成镜像测试数据时,选择镜像子域不是完全随机的,是受限制的随机选择方式.
假 设n维 输 入 空 间 为D={(d0,d1,…,dn-1)|d0∈D0,d1∈D1,…,d(n-1)∈D(n-1)},镜像划分深度为ω,则每个维度被划分为2ω个区域,整个输入空间被划分为2n·ω个镜像子域. 第i维空间di被划分的区域用dij表示,其中0 ≤j≤2ω-1.
定义∑ij表示第i维空间di的第j个区域中被选中的镜像子域的数量. 当∑ij=2ω()n-1时,表示第i维空间di的第j个区域中所有镜像子域都被选出.
对于某个子域X={(x0,x1,…,xn-1)},定义δ(xi)表示子域X在第i维空间中所属的子域位置. 镜像受限选择算法描述如算法2所示.

算法2 镜像受限选择序算法输入:输入空间D;输出:子域选择序;1. 镜像划分深度为ω,划分子域数量m=2n·ω,初始∑ij=0,其中0 ≤i ≤n-1,0 ≤j ≤2ω-1.2. 随机选择一个子域作为源域Ds={(d'0,d'1,…,d'n-1)|d'0 ∈D0s,d'1 ∈D1s,…,d'n-1 ∈D( )n-1 s,0 ≤s ≤2ω-1}将源域空间对应每个维度的区域数量加1,即∑ij=1,其中,i ∈{0,1,…,n-1},j=δ(d'i).3. 在所有∑ij=0的子域内,随机选择一个子域D',同理,将该子域对应的每个维度的区域数量加1,∑ij=1,其中j=δ(D'i).4. 当所有子域全部对应的∑ij=1时,重复此操作,在所有∑ij=0的子域内,随机选择子域. 直至所有子域全部被选出.5. 返回子域选择出的顺序.
如图4所示,在二维输入空间中,镜像划分深度为2,则每个维度被划分成4部分,二维空间被划分为16个镜像子域. 随机选择一个子域作为源域,如图4(a)中,标号为1的子域,则δ(x0) =1,δ(x1) =1,故∑01=1,∑11=1. 即阴影区域为源域“1”在每个维度上的子域所占的区域,下一个镜像子域的选择不在阴影区域内选择. 也就是在图4(a)中的空白子域中,随机选择一个域作为镜像子域“2”,如图4(b)所示,则“2”子域的δ(x0) =2,δ(x1) =3,故∑02=1,∑13=1. 即“2”子域所在的行列子域转换为阴影区域.同理,在空白子域中随机选择“3”、“4”子域(如图4(c)、(d)),第一轮子域选择结束后,每个维度的每个区域都有选出的镜像子域,即∀(i,j) ∑ij=1,如图4(d)中所有子域全部为阴影填充.
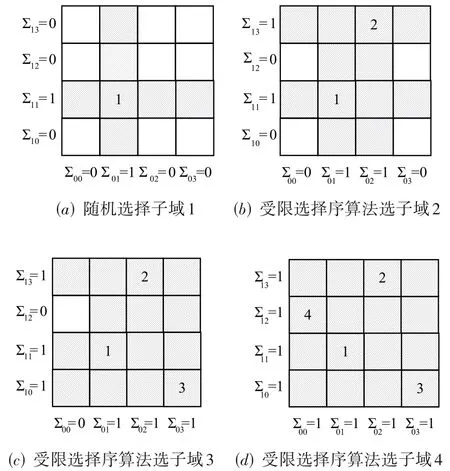
图4 镜像受限选择序
然后依此规则,开始第二轮迭代,选出相应的镜像子域,第二轮迭代结束后,每个维度的每个区域都有选出的2 个镜像子域,即∀(i,j) ∑ij=2,第k轮次迭代后,∀(i,j) ∑ij=k,直至k=2ω()n-1时(图中示例k=4 时),全部镜像子域被选出.
有时可能会出现镜像子域受限选择冲突现象,如图5所示.
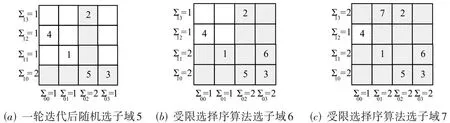
图5 镜像受限选择序冲突现象
当第一轮迭代结束后,∀(i,j) ∑ij=1,此时清空所有阴影底纹,恢复为白色,开始第二轮迭代,从剩余的空白镜像子域中随机选择一个,如图5(a)所示,选择镜像子域“5”. 如图5(a)所示,则“2”子域的δ(x0) =2,δ(x1) =0,故∑02=2,∑10=2. 即“5”子域所在的行列子域转换为阴影区域. 同理,在空白子域中随机选择“6”、“7”子域(如图5(b)、(c)),此时,仅剩∑00=1,∑12=1,其余∑ij=2,i∈{0,1}. 而仅剩的白色子域“4”已经被选出,此现象为镜像子域受限选择冲突现象. 算法针对此情况的冲突解决方案是,清空所有阴影底纹,恢复为白色,然后从所有空白且没有标号的子域中随机选择一个子域,进入下一轮迭代,直至所有子域均为选出.
4.3 基于镜像受限选择序的MART算法
根据镜像受限选择序思想,本文提出了基于镜像受限选择序的MART 算法. 通过限制待镜像的镜像域,使得镜像域的选择序更加均匀,保证了测试数据尽可能的在每个维度上均匀分布.

算法3 基于镜像受限选择序的MART算法输入:n维输入空间,镜像深度ω;输出:测试数据集E.1. 对于n维输入空间,镜像深度ω,将输入域划分为2n·ω个子域.2. 从子域中任选一个作为源域,其余子域为镜像域.3. 源域中使用ART算法生成测试数据tc,放入E中.4. 测试数据tc执行被测程序若触发缺陷,转向步骤6,否则通过镜像函数映像生成镜像测试数据tc'.5. 镜像测试数据生成顺序取决于镜像选择序(参考算法2:镜像受限选择序算法),其中检验生成的镜像测数据tc'(放入E中)是否触发缺陷,若触发缺陷,转向步骤6,否则到步骤3.6. 算法终止,返回已生成测试数据集E.
如图6所示,在二维输入空间中,镜像划分深度为2时,整个输入空间被划分为16个子域,假设选取标号为“1”的子域空间为源域,即在1 号子域中根据ART 算法生成测试数据. 根据镜像受限选择序MART 算法的基本思想,依次选择镜像子域通过镜像函数生成镜像测试数据t. 第2 号子域被随机选出,只须保证与1 号子域不同行不同列. 同理,第3 号子域被随机选出,只须保证与1、2号子域不同行不同列. 第一轮次选出的4个子域如图6(a)所示,依此原则,第二、三轮每轮次内依次选择不同行不同列的子域,如图6(b)(c)所示. 直至第4轮次执行完毕,如图6(d)所示,所有16个镜像子域被选出,生成子域序列s. 在源域中使用ART 算法生成的测试数据根据镜像函数,按照子域序列s的顺序依次生成测试数据,每次生成一个镜像测试数据,执行被测程序检验是否触发缺陷,如果触发缺陷则算法终止,否则依次执行完序列s中所有的测试数据,若还未发现缺陷,则需在源域中根据ART 算法生成第二个测试数据,以上述原则产生镜像子域的选择序,生成镜像测试数据,直至发现缺陷或达到迭代终止条件.
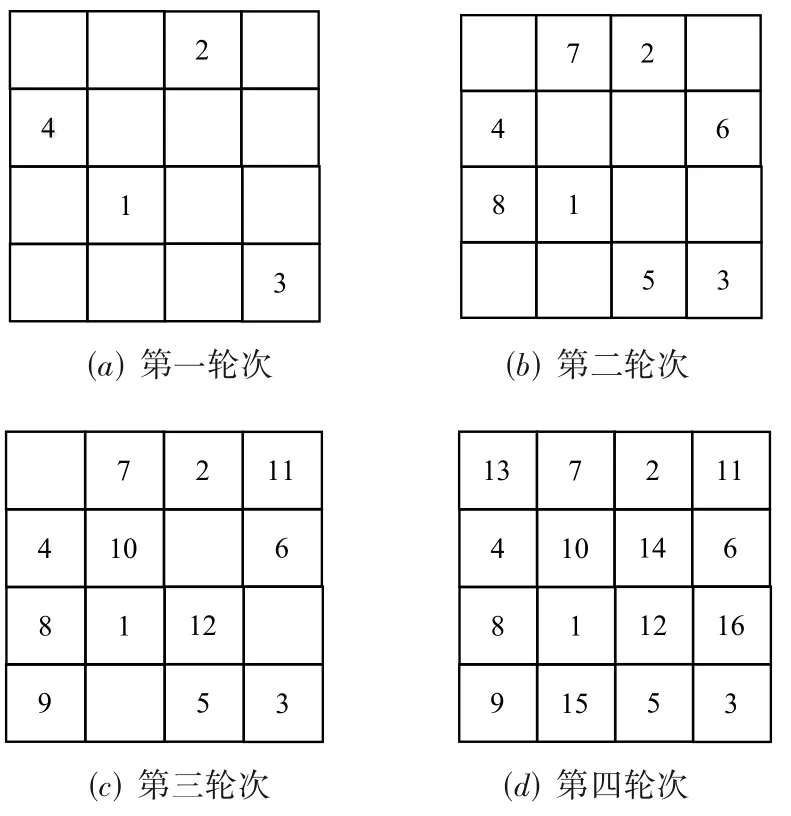
图6 基于镜像受限选择序的MART算法
5 实验设计与结果分析
5.1 仿真实验
5.1.1 实验设计
仿真实验涉及的参数主要为维度、失效率、失效模式、测试方法、实验次数等,具体如下:
(1)维度. 表示待测程序输入参数的个数. 假定以二、三、四、五维输入域进行分析对比,每个维度坐标取值范围为[1,1 000],如二维输入域为正方形,三维输入域为正方体,以此类推.
(2)失效率. 为引发失效的输入域占整个输入域的比例,显然,失效率θ∈[0,1]. 失效域大小由失效率确定,失效率=块状失效模式大小/整个输入空间大小,失效域的位置随机出现在输入域内. 失效率取值范围为θ∈[0.000 1,0.1].
(3)失效模式. 使用代码模拟输入空间中的块状失效模式、条状失效模式和点状失效模式. 根据实验设置的输入空间大小D,失效率θ,计算失效区域F=D×θ.块状失效模式模拟在输入空间内随机生成一个面积或体积为F的正方形(二维)或立方体(三维)区域;条状失效模式模拟在输入空间中的一个长条区域,通过在X轴、Y轴正向坐标轴上各自随机选取一个点,两个点连接后的直线作为长条失效域的长度,宽度由失效域面积F确定,使得长宽比例围成的条状区域面积为F;点状失效模式模拟在输入空间内随机生成k个不相交的相等大小的正方形区域,假定每个正方形的面积为S,则k个正方形区域面积之和k×S等于失效域面积F,本实验中k取值为10,即模拟10个离散点状失效域. 失效模式的影响分析时,考虑三种失效模式,除此之外,无特殊说明时,失效模式均为块状失效模式.
(4)测试数据生成算法. 实验算法为ART 算法、镜像顺序选择序MART 算法、镜像随机选择序MART 算法、镜像受限选择序MART 算法. 三类MART 算法均采用对等划分的方式对输入空间进行子域划分,镜像函数包括平移和对称两种. 源域中测试数据生成算法均采用FSCS算法. 详见表1.
表1 实验中的算法列表
随机测试(RT):随机测试算法,Fmeasure理论值为1/θ(其中θ为失效率).
ART 算法:为ART 算法中的经典DART 算法之一FSCS算法,基于距离计算的自适应随机测试算法,其中候选测试数据集大小设为10.
镜像顺序选择序MART 算法:镜像子域选择方式为顺序方式. 镜像随机选择序MART 算法:镜像子域选择方式为顺序方式. 镜像受限选择序MART 算法:为4.3节提出的新算法.
(5)检错有效性度量指标. 使用各类算法生成测试数据,当测试数据落入模拟的失效域中时,触发缺陷,记录第一个发现缺陷时已生成测试数据的数量. 每次执行算法发现第一个缺陷所需的测试数据的数量为Fcount,则本实验中Fmeasure值为10 000次Fcount的平均值.算法有效性度量采用Fmeasure值,是首次触发缺陷生成测试数据数量的期望值. 为了便于对比不同失效率下ART 算法相对RT 算法的Fmeasure改进程度,定义Fratio=FARTFRT,Fratio反映了ART 算法相对RT 算法的改进程度. 若Fratio<1,则说明ART 算法检错有效性比RT 算法强,当Fratio≥1 时,说明ART 算法相对RT 算法检错有效性无优势.
(6)数据展示标识. 实验结果图形展现时,ART 算法使用黑色实线标识,使用平移镜像函数的各类MART算法(MART_T、MART_T、MART_T_N)使用实线标识(分别对应品红色、蓝色与红色),使用对称镜像函数的各类MART 算法(MART_R、MART_R_R、MART_R_N)使用虚线标识(分别对应品红色、蓝色与红色).
5.1.2 实验结果分析
5.1.2.1 失效模式的影响分析
二维输入空间中,镜像划分深度为2,划分子域数量为16 时;以及镜像划分深度为3,划分子域数量为64时,分析各类MART 算法在块状失效模式、条状失效模式和点状失效模式下检错有效性.
如图7(a)(b)所示,块状失效模式中,镜像深度为2时,各类MART 算法中,镜像平移函数的MART 算法优于镜像对称MART 算法. 镜像深度为3 时,同类MART算法中镜像平移函数的MART 算法与镜像对称MART算法差异不大. MART_T_N 算法在各类MART 算法中检错有效性最强.
如图7(c)(d)所示,条状失效模式下,镜像顺序选择序算法在各类MART算法中表现优异,Fratio值小于其他算法. 分析镜像顺序选择算法在条状失效模式下的优势,主要由模拟仿真方式决定. 因为条状模式代码中失效区域与X轴、Y轴的正向轴相交,而镜像顺序选择算法的顺序也是从坐标原点开始,沿X轴依次顺序选择,然后向Y轴正向方向扩展. 这种条状失效模式模拟方式有利于镜像顺序选择序触发缺陷,所以该类算法Fratio值较小.
如图7(e)(f)所示,点状失效模式下,各类ART 算法检错有效性增强. 随着深度增加,各类算法检错有效性均有所降低. 整体来看,MART_T_N 算法检错有效性略强于其他MART算法.
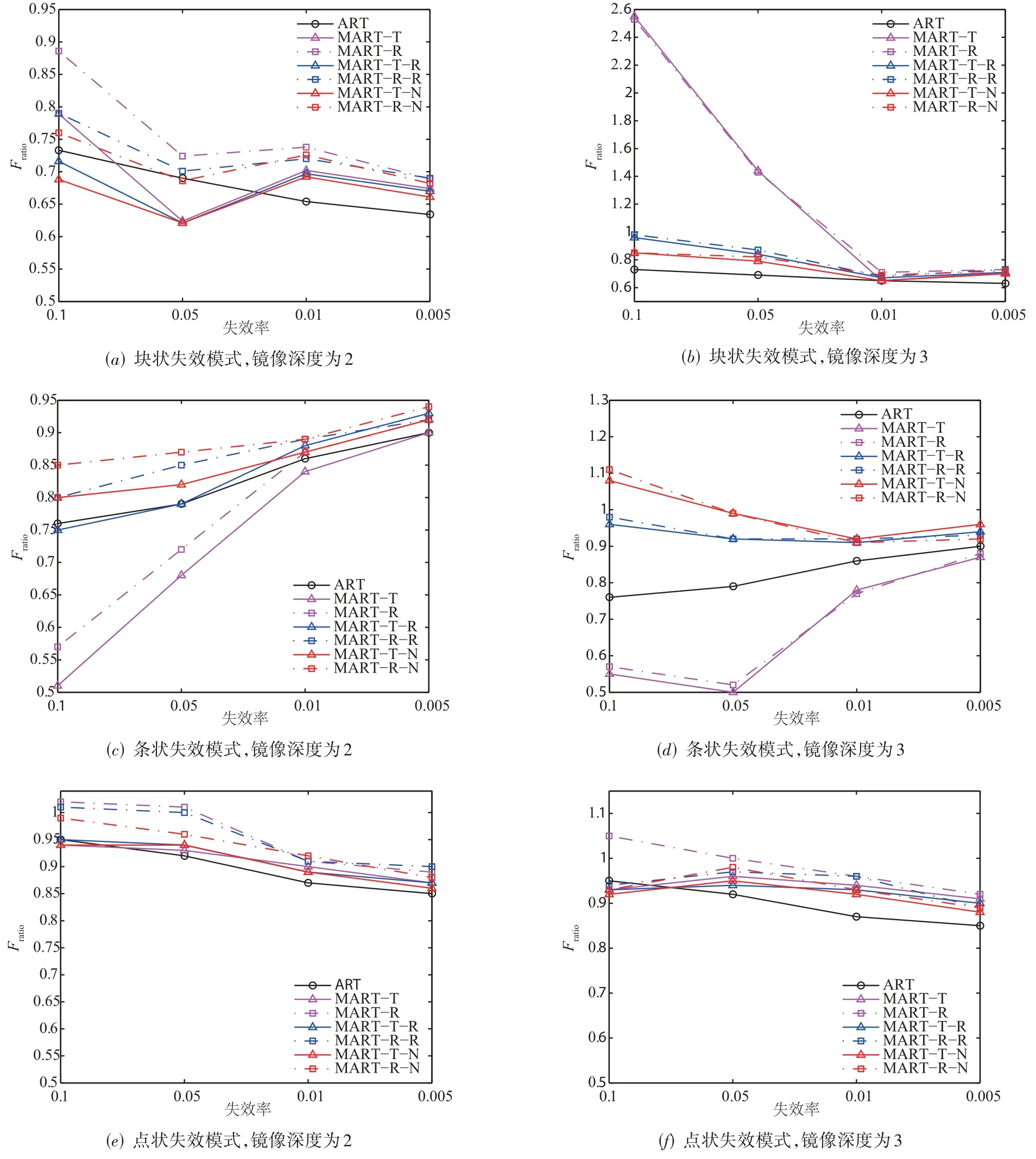
图7 不同失效模式,2~3镜像深度,各类算法Fratio值
三种失效模式下,各类ART 算法都随着镜像子域增多,检错有效性有所降低.MART_T_N 算法在块状失效模式与点状失效模式中较其他MART 算法相比检错能力略强.
5.1.2.2 镜像划分的影响分析
分析镜像划分深度不同时,ART算法及各类MART算法的有效性对比. 失效率为0.01时,镜像深度分别取ω=1,2,3,4,二维空间时子域数量为4、16、64、256,三维空间时子域数量为8、64、512、4 096. 对比实验Fratio值如图所示.
图8 中,不同镜像深度时,平移镜像函数普遍优于对称镜像函数,三维空间中,平移镜像函数的优势比在二维空间中更大.MART_T_N 算法在三维空间,深度为4时,较MART_T_R算法优势明显.
总得来说,当镜像划分的子域数量与RT 算法的理论Fmeasure值相近时,各类MART 算法的检错能力最强.镜像划分的子域数量增大时,各类MART 算法的检错能力都下降. 镜像受限选择序算法检错有效性优于其他MART 算法. 随着深度的增加,MART_T_N 算法优势更加明显.
5.1.2.3 维度的影响分析
(1)镜像划分深度相同,维度不同
失效率为0.01(RT 算法理论Fmeasure值为100),2~6维输入,镜像划分2,各算法Fratio值如图9.
在低维空间中,不同镜像序的MART 算法差异不大,随着维度的增大,MART_T_N 算法比MART_T_R 算法的优势增大,除了当维度和深度确定的子域数量与RT 的理论Fmeasure值近似时,各类MART 算法的Fratio值最低.
(2)划分子域数量相同,维度不同
分别考虑失效率为0.01 时与0.001 时,不同维度时而相同子域数量进行实验验证.
本次实验设置失效率为0.01 时(RT 算法理论Fmeasure值为100),子域数量最接近的值为64,分别对2、3、6维输入空间进行镜像划分3、2、1时得到64个子域,各算法的Fratio值如图10(a)所示. 实验设置失效率为
图8 失效率0.01,2~3维空间,划分深度1~4,各算法Fratio值
图9 失效率0.01,镜像深度为2,2~6维度各算法Fratio值0.001 时(RT 算法理论Fmeasure值为1 000),子域数量最接近的值为1 024,分别对2、5 维输入空间进行镜像划分5、2时得到1 024个子域,各算法的Fratio值如图10(b)所示.
图10 子域数量与RT理论Fmeasure相近时,各算法Fratio值
如图10 所示,在失效率0.01 与0.001 时,在子域数量与RT 算法的理论Fmeasure值相近时,各类平移镜像函数MART 算法(MART_T、MART_T_R、MART_T_N)的检错有效性最强,并且对维度变化不敏感.ART 算法、各类对称镜像函数MART 算法(MART_R、MART_R_R、MART_R_N)受维度变化影响大,随着输入空间维度增大,Fratio值增大.
5.1.2.4 失效率的影响分析
由于镜像顺序选择序MART 算法在子域数量大于RT 的理论Fmeasure值时,检错有效性迅速下降. 所以下面分析只涉及到镜像随机选择序MART 算法、镜像受限选择序MART算法.
分析在三维输入空间中,失效率分别为0.1、0.05、0.01、0.005、0.001时(RT 的理论Fmeasure值为10、20、100、200、1 000),镜像深度分别取ω=1,2,3,4,子域数量分别为8、64、512、4 096,ART 算法、镜像随机选择序MART 算法、镜像受限选择序MART 算法的Fratio值如图11所示.
(1)不同失效率时,Fratio值分析
深度为1、2、3 对应的子域数量(8、64、512)与失效率0.1、0.01、0.005(RT 的理论Fmeasure值为10、100、200)相近. 如图11(a)、(c)、(e)所示,失效率为0.1、0.01、0.001 时,镜像平移函数的MART 算法分别在深度为1、2、3 时Fratio值最低,且MART_T_R、MART_T_N 算法Fratio值相近. 随着深度的增大,MART_T_N 算法比MART_T_R算法的优势增大,Fratio值差距增大.
如图11(a)、(b)、(d)所示,各类MART 算法的Fratio值都高于ART 算法,随着深度的增加,子域数量的增多,MART_T_N 算法与MART_T_R 算法的Fratio值差异增大,优势增大.
(2)不同失效率时,Fratio值分析
分析MART_T_N 算法在镜像划分深度分别为1、2、3、4时的表现,以便指其在实际应用中镜像划分深度参数的设置.
如表2 所示,镜像划分深度与RT 算法的理论Fmeasure值相近时,MART_T_N 算法具有较高的检错能力,甚至优于ART 算法的Fratio值. 整体来看,随着镜像划分深度的增加,子域数量的增大,MART_T_N 在各失效率下检错能力下降.
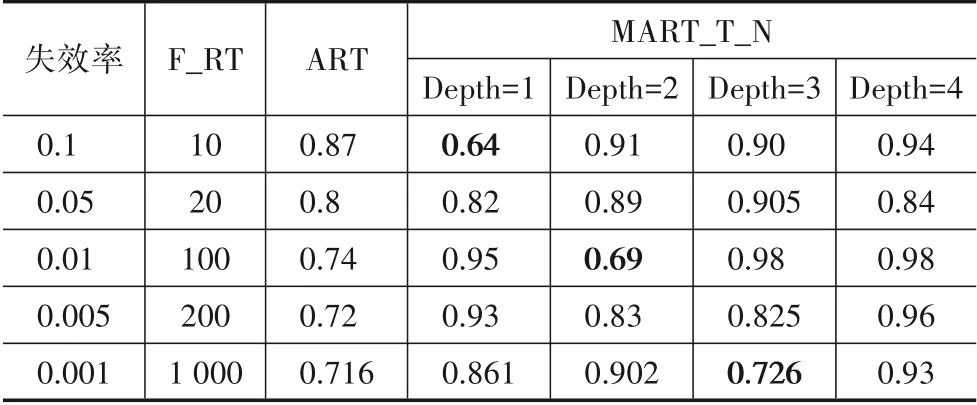
表2 不同失效率,不同深度下MART_T_N算法的Fratio值
5.2 实例实验
5.2.1 实验设计
5.2.1.1 测试基准程序
本次实验有四个真实程序,其中Trityp 程序和TCAS 程序是来源于Software artifact Infrastructure Repository(SIR)的被测程序.Integer 程序源于JDK 中java.lang.Integer 类. DSCompiler 类来源于org.apache.commons.math3.analysis.differentiation包. 详情如表3所示.
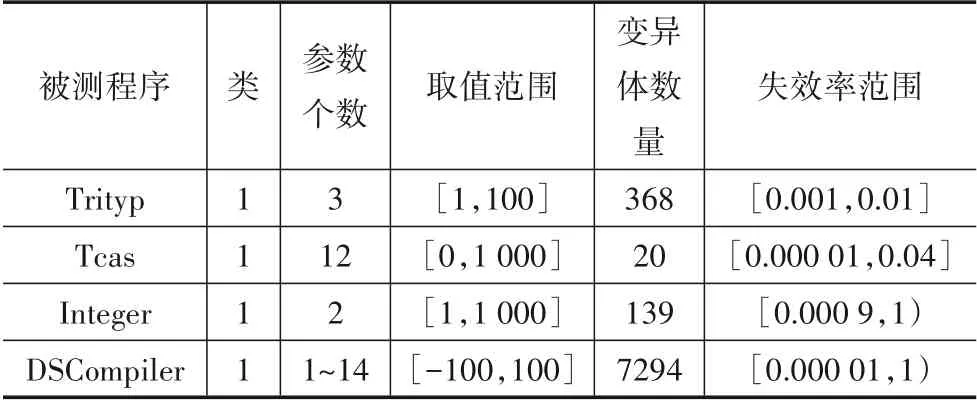
表3 四个实例被测程序的详情
Trityp 程序为三角形分类程序,3 个整型输入作为三边长度,输出是否能构成三角形以及属于哪类三角形.Mujava 变异测试工具用来生成被测程序的变异体,每个变异体是在源程序中注入一个错误来生成的.Trityp 程序一共生成462 个变异体. 去除72 个等价变异体,剩余390 个变异体. 假定整型输入域范围为[1,100],每个变异体的失效率通过程序输入参数遍历整个输入域计算得到. 实验选择失效率在(0.000 1,1)范围内的368个变异体.
TCAS是经典的西门子程序之一,是有12个输入参数的防撞系统源代码. 输入域范围为[0,1 000]. 变异体来源于SIR,这些变异体种的失效源于真实的错误.变异体失效率在[0.000 01,0.04]范围内.
Integer 程序源于JDK 中java.lang.Integer 类,2 个输
图11 在3维空间,各算法1~4深度的Fratio值(除顺序镜像序)入参数取值范围为[1,1 000]. Integer 程序使用mujava生共160 个变异体,去除21 个等价变异体,剩余139 个变异体的失效率在[0.000 9,1)范围内.
DSCompiler 类来源于org.apache.commons.math3.analysis.differentiation 包,Apache Commons 类 库 中math3 类库为轻量级数学和统计组件. 使用Mujava 生成共计7 294 个变异体,失效率为[0.000 01,1)范围内.
5.2.1.2 实验参数设置
本实验对比的镜像随机选择序算法、镜像受限选择序算法. 通过第5.1 节仿真实验分析,平移镜像函数在MART 算法中较对称镜像函数更有效,所以本实验只考虑平移镜像函数.
镜像随机选择序MART算法(MART_T_R):采用对等划分的方式对输入空间进行子域划分,镜像函数为平移镜像函数,镜像子域选择方式为随机序方式,源域中测试数据生成算法采用FSCS算法.
镜像受限选择序MART 算法(MART _T_N):为本文提出的方法,镜像函数为平移镜像函数.
实验执行过程如下:分别使用MART_T_R 和MART_T_N 算法生成测试数据,执行源程序及变异体.若变异体与源程序运行结果不同,则此算法杀死该变异体,记录当前已生成测试数据数量.
针对每个有效变异体,分别记录MART_T_R 和MART_T_N 杀死该变异体所需测试数据数量F-count,实验重复2 000 次均值作为Fmeasure. 令Frandom与Fnew分别 表 示MART_T_R 和MART_T_N 的Fmeasure,Fratio为MART_T_N 与MART_T_R 的Fmeasure比值,即MART_T_N 算法相对MART_T_R 算法检错有效性改进程度. 若Fratio<1,说明MART_T_N算法优于MART_T_R算法.
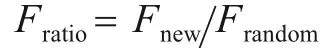
5.2.2 实验结果分析
四个程序使用MART_T_R 和MART_T_N 运行后的Fratio值统计结果如表4所示. 表中列出每个程序变异体数量,统计出MART_T_N 算法与MART_T_R 算法的Fratio值大于等于1和小于1的情况. 在Trityp程序的368个变异体中,Fratio<1 的变异体数量为294 个,即79.9%的变异中,MART_T_N 算法的检错能力优于MART_T_R 算法.Integer 程序的139 个变异体中,Fratio<1 的变异体数量为112 个,即80.6%的变异中,MART_T_N 算法的检错能力优于MART_T_R 算法. TCAS 程序的20 个变异体中,Fratio<1 的变异体数量为16 个,即80%的变异中,MART_T_N 算法的检错能力优于MART_T_R 算法.DSCompiler 类的7 294 个变异体中,Fratio<1 的变异体数量为5 568个,即76.3%的变异中,MART_T_N算法的检错能力优于MART_T_R算法.
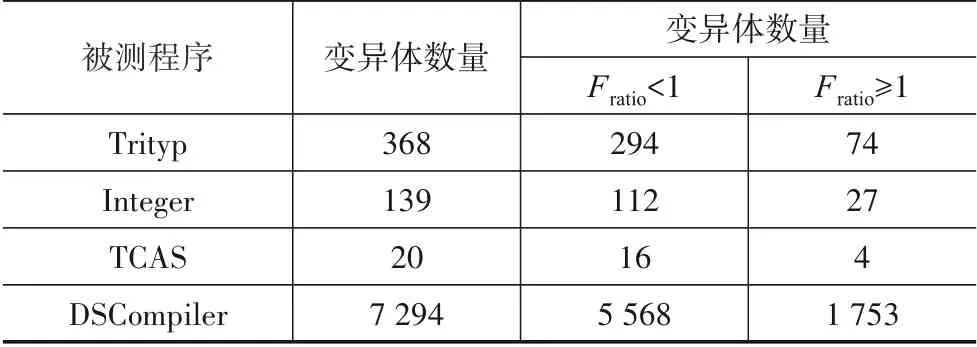
表4 实例程序变异体Fratio结果
在实例实验中,从MART_T_N 算法对各变异体检错能力来看,MART_T_N 算法在实际程序代码中,具有高于MART_T_R算法的检错能力.
6 小结
镜像策略将输入域划分多个镜像子域,通过镜像函数将源域中测试数据生成方法生成的测试数据镜像到各镜像子域中,从而生成整个输入域内的测试数据.将镜像策略用于ART 算法的测试数据生成过程中,减少了ART 算法的计算开销,通过镜像函数即可生成镜像测试数据.
但镜像策略融入ART 算法后,虽然提高了测试数据生成的效率,但降低了算法的有效性. 本文对MART算法进行了研究,针对镜像函数将源测试数据镜像到各子域时的镜像顺序,对比分析镜像选择序与镜像函数对MART 算法的影响,提出了基于镜像受限选择序的MART 算法. 实验结果显示,针对镜像策略中镜像选择序的优化,提高了MART 算法的检错有效性,得到以下结论:
(1)镜像平移函数的MART 算法多数情况下优于镜像对称函数的MART算法,或与其相当;
(2)当镜像划分的子域数量与RT 算法理论Fmeasure值相近时,各类MART算法检错能力最强.
(3)当划分子域数量大于RT算法理论Fmeasure值,镜像选择序对MART 算法影响较大. 镜像顺序选择序的MART 算法的检错能力急速下降,所以,不适宜用于镜像划分子域数量较多的场景.
(4)本文提出的镜像受限选择序MART 算法检错有效性高于镜像随机选择序MART 算法. 随着镜像划分深度、输入空间维度越大,镜像受限选择序MART 算法的优势越明显.

