矩阵信息几何中值检测器

华小强，程永强，王宏强，王勇献，张理论

（1. 国防科技大学气象海洋学院，湖南长沙 410079；2. 国防科技大学电子科学学院，湖南长沙 410079）

1 引言

信号检测是信号处理中的重要内容，被广泛应用于雷达、声纳以及通信等领域. 经典的信号检测方法，如广义似然比（Generalized Likelihood Ratio Test，GLRT）检测器［1］、自适应匹配滤波（Adaptive Matched Filter，AMF）［2］以及单元平均恒虚警（Cell Averaging Constant False Alarm Rate，CA-CFAR）检测器［3］等，受杂波协方差矩阵估计性能的影响较大，通常，杂波协方差矩阵估计精度越高，其检测性能越好. 杂波协方差矩阵估计性能与满足独立同分布的样本数紧密相关，已证明，当样本数K大于或等于2 倍的矩阵维数n时，杂波协方差矩阵的估计精度较高，其检测性能损失低于3 dB［1，4］. 然而，在实际应用中，检测背景通常具有小样本、非均匀特性，独立同分布的样本数K难以满足K≥2n的假设，同时，样本数据中难以避免地存在干扰数据，使得杂波协方差矩阵的估计性能急剧下降. 小样本、非均匀杂波下的信号检测问题是信号处理中的一个难点问题，因此亟需提升检测器的性能.

为了提升小样本、非均匀杂波下的信号检测性能，一种常用的方法是借助于辅助知识. 文献［5］在已知一些子空间基向量的条件下，利用观测数据在贝叶斯框架下推断出未知基向量，从而将干扰表示成基向量的线性组合，以提升信号检测的抗干扰能力. 文献［6］利用地理信息系统的栅格模型来表示雷达的观测场景，并假设雷达距离单元与栅格大小相等，通过判断栅格的属性值是否相近来选择均匀样本数据，从而提高了杂波协方差矩阵的估计性能. 文献［7］将干扰协方差矩阵表示成几个先验谱模型的线性组合，利用观测的样本数据来估计系数，由此设计了一种广义似然比检测器，以提升小样本下信号检测的性能. 基于知识辅助方法的主要目的是提升小样本下协方差矩阵的估计精度并增强非均匀杂波下协方差矩阵的鲁棒性［8～12］，这类方法依赖杂波环境的统计特性，然而，在实际应用中，杂波环境的统计特性难以准确获取，这极大限制了杂波协方差矩阵的估计性能.

法国泰雷兹空气系统研究员Barbaresco 提出了一种基于矩阵流形的信号检测方法［13］，该方法假设每一个样本数据服从零均值的复高斯分布，计算待检测单元的托普利兹正定矩阵与辅助样本数据的均值矩阵之间的黎曼距离，并将其与检测门限进行比较，以得到是否存在目标的判断. 与基于快速傅里叶变换（Fast Fourier Transform，FFT）的CFAR 检测器相比，基于矩阵流形的信号检测方法在小样本条件下的飞机尾流检测中展现出了较大的性能优势［14～17］. 在此信号检测方法的基础上，文献［18，19］探索利用不同区分能力的散度度量来代替黎曼距离，得到不同基于信息散度的信号检测器，由于不同度量所反映出来的流形几何结构不同，所得检测器的性能也不一样. 文献［20～22］在矩阵流形上定义了2 类新的度量，即Total Bregman 散度和Total Jensen-Bregman，并分析和验证了2 类度量方法的鲁棒性和区分能力. 文献［23］定义了影响函数，系统推导了干扰样本对散度均值的影响，分析了不同均值的鲁棒性. 文献［24～27］提出了一种预处理方法，在矩阵流形上对正定矩阵进行滤波处理，以减少信息冗余，提升矩阵间的区分性. 上述工作均围绕着矩阵流形上度量的区分性及其均值的鲁棒性进行研究，取得了一些有意义的结果.

本文在上述工作的基础上，在矩阵信息几何理论的框架中提出几何中值检测器，将信号检测问题转化为矩阵流形上两点间的几何结构差异性问题来研究，从样本数据中提取出相应特征信息并建模为一个正定矩阵，通过区分流形上含目标信号的矩阵和杂波对应的矩阵来实现信号检测. 此外，基于矩阵流形上度量的各向异性，定义了度量的区分能力描述子，系统分析了不同几何度量在矩阵流形上的区分能力差异. 通过仿真实验，分析了该检测器对样本数和干扰的鲁棒性，并验证了在小样本、非均匀杂波下的性能优势. 最后，给出了影响该检测器性能的几方面因素，为进一步提升检测性能指明了方向. 同时，基于此检测器的思想，可为后续非平稳信号检测、扩展目标检测等问题的研究奠定基础.

2 矩阵信息几何检测器原理

矩阵信息几何检测器是从样本数据中提取出特征信息，并建模为一个正定矩阵，在矩阵流形上通过区分含目标信号的矩阵与杂波矩阵来实现信号检测. 下面首先介绍矩阵信息几何的基本知识，然后给出矩阵信息几何检测器的基本原理.

2.1 矩阵信息几何的基本知识

矩阵信息几何是在矩阵流形上研究矩阵类型数据信息处理的一套方法，是信息几何理论［28～33］在实际应用中发展较快的一套理论体系. 矩阵信息几何是在流形上采用微分几何方法来研究数据模型的内蕴信息的一套理论. 许多信息处理问题，如目标检测［34，35］、分类与识别［36］等问题均可转化为矩阵流形上的几何问题来研究. 利用矩阵信息几何来研究信息处理问题，可以透过现象认识问题的几何本质，为问题的解决提供新的视角.

矩阵流形是矩阵信息几何理论的研究基础，通常所指的矩阵为正定矩阵，对于一个n×n矩阵A，如果∀x∈Rn，x≠0，二次型xTAx＞0，则矩阵A是正定，记A＞0. 所有的n×n矩阵构成了一个空间P(n)，即

空间P(n)构成了一个具有非正曲率的矩阵流形. 对于常用的对称正定矩阵空间，其构成的矩阵流形具有以下较好的性质：

（1）它是一个封闭的、非多面体的自对偶凸锥；

（2）它包含一个规范的高阶对称空间；

（3）它的内部是一个可微黎曼流形.

上述良好的性质，可为实际应用带来许多意想不到的性能增益.

在矩阵流形上，需要定义度量张量来刻画长度的刻度，对于流形P(n)上的一点P，常用的黎曼度量张量可由下式的微分来定义［37］：

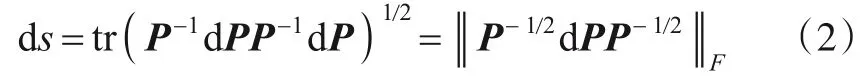
基于此微分形式，可在点P的切空间中定义内积［37］，即

相应的范数可定义为

在矩阵流形上，两点间的连接通常由沿着流形曲面的曲线给出，其中最短的路径称为测地线，对于流形上的两点A和B，其间的测地线由下式给出［38］：

通过测地线，可分析从点A到点B之间的路径，两点A和B之间的测地线长度称为测地线距离，即仿射不变黎曼度量（Affine Invariant Riemannian Metric，AIRM）或黎曼距离，可由下式给出［38］：

其中，λi是矩阵的第i个特征值.

2.2 几何检测器的基本原理

矩阵信息几何检测器与传统检测器最大的区别在于将信号检测问题转化为矩阵流形上的几何问题来研究，并利用矩阵流形的几何结构差异来区分目标信号与杂波间的特征信息. 对于每一个样本数据，提取出合适的特征信息，并将其建模为一个正定矩阵，则样本数据信息均包含在正定矩阵中. 在矩阵流形上，通过几何距离度量目标信号矩阵与杂波矩阵间的差异大小，并与检测门限进行比较以实现对是否存在目标的判决.为了获得较为精确且稳定的杂波矩阵，通常根据辅助样本数据来估计杂波协方差矩阵，在矩阵流形上，取辅助样本数据矩阵的中值作为杂波矩阵的估计，矩阵信息几何检测器的基本原理如图1所示.

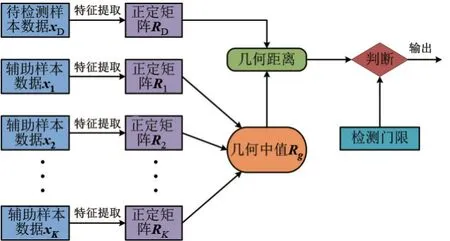
图1 矩阵信息几何检测器的基本原理

通常，杂波协方差矩阵是由辅助样本数据估计得到的，对于一组独立同分布的辅助样本数据集{x1，x2，…，xK}，其样本协方差矩阵（Sample Covariance Matrix，SCM）由下式估计得到：

式（7）实质上是K个秩为1 的自相关矩阵xi xHi(i=1，2，…，K)的代数均值，xi xHi是第i个样本数据的自相关矩阵，从xi到xi xHi可看成是从样本数据中提取出相关特征的过程，xi xHi是xi的特征矩阵. 基于此相关信息的特征矩阵，可以估计得到杂波协方差矩阵. 通常，矩阵集构成了一个非线性空间，式（7）的代数均值并未考虑到空间的非线性几何结构，一般认为，非线性矩阵空间是一个矩阵流形，与欧氏空间中的代数均值相对应，在流形上，几何中值可表示矩阵集的中心. 为了便于分析，秩为1 的自相关矩阵xi xHi(i=1，2，…，K)需要满足正定性，常用的正定化方法有以下2种：

（1）矩阵xi xHi是样本数据xi的极大似然估计，可采用其次优解来代替，对于一个样本数据x=[x0，x1，…，xn-1]T，其次优解的估计为

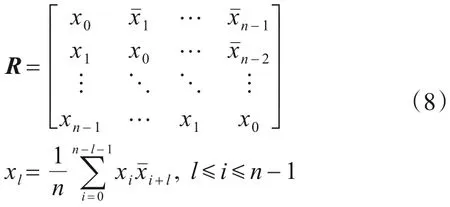
（2）矩阵xi xHi的对数加载形式为

其中，I是单位阵，λ是控制因子.

对于自相关矩阵xi xHi(i=1，2，…，K)，可得到相应的正定矩阵Ri(i=1，2，…，K)，由此可估计出流形上的几何中值矩阵Rg，即杂波协方差矩阵的估计. 矩阵信息几何检测器就是通过比较待检测样本数据x D对应的矩阵RD与几何中值矩阵Rg之间的几何距离与检测门限之间的大小，从而得出是否存在目标的判决，其检测原理如下式：

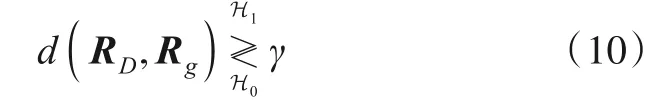
其中，d( ·，·)表示两矩阵间的几何距离，γ表示检测门限，H0表示不存在目标信号的假设，H1表示存在目标信号的假设. 从式（10）可以看出，矩阵信息几何检测器的性能和几何距离所度量出RD与Rg之间的差异性密切相关. 事实上，流形上的几何距离反映了流形的几何结构，不同的几何距离反映出的几何结构不同，对流形上两点间的区分能力也不相同. 此外，在存在干扰的情况下，中值矩阵的鲁棒性也对检测器的性能有一定的影响，鲁棒性越好，检测性能越稳定. 因此，选取区分能力强的几何距离以及估计出鲁棒性强的几何中值，对提升检测器的性能至关重要. 本文的主要目的是在矩阵信息几何理论的框架中设计一个新的信号检测器，定义几何距离度量的区分能力描述子，为后续检测器的研究奠定基础.

3 几何距离度量及其中值

矩阵流形上不同的几何距离度量反映了不同的几何结构，依据不同的几何距离，可以定义不同的几何中值. 下面首先介绍几种几何距离度量，并分析其流形几何结构差异；然后给出相应的几何中值定义，并推导其计算公式.

3.1 几何距离度量

在矩阵流形上，常用的AIRM［38］具有许多优良性质，但由于其计算复杂度较高，在实际应用中，通常用对数欧几里德距离度量（Log-Euclidean Metric，LEM）［39］来代替，与AIRM一样，LEM是在流形的切空间定义的测地线距离，具有距离度量的数学性质. 除了测地线距离外，矩阵流形上还可定义许多散度度量，如库尔贝克-莱布勒散度（Kullback-Leibler Divergence，KLD）［40］、对称库尔贝克-莱布勒散度（Symmetric Kullback-Leibler Divergence，SKLD）［40］以及詹森-布雷格曼洛格德特散度（Jensen-Bregman LogDet，JBLD）［41］等，这些散度都具有一些良好的特性，并得到了广泛的应用. 在这些几何度量中，AIRM、SKLD和JBLD具有仿射不变性，即对于n×n的可逆矩阵M，距离度量函数满足δ2(A，B) =δ2(MAMH，MBMH).下面给出4种几何距离度量的具体定义.

定义1对于矩阵流形P(n)上的两点X1和X2，其间的LEM距离为［39］

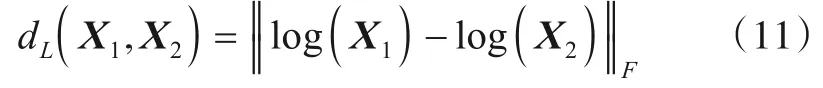
定义2对于矩阵流形P(n)上的两点X1和X2，其间的KLD为［40］

定义3对于矩阵流形P(n)上的两点X1和X2，其间的SKLD为［40］

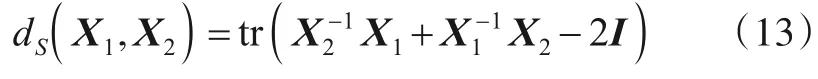
定义4对于矩阵流形P(n)上的两点X1和X2，其间的JBLD为［41］

不同的距离度量反映出的流形几何结构不同，流形的局部几何结构可由流形上某点的局部等位球来表征.在欧氏空间中，以一点为球心的单位球是一个标准的圆球，这是因为欧氏空间的度规是一个单位阵，即张成空间的各方向的单位基向量的长度相同；而流形空间中，其度规并非是一个单位阵，张成空间的各方向的单位基向量长度不同，所画出的单位球并不是标准的圆球.

为了从视觉上展示不同度量所反映出的几何结构差异，以3 维单位阵为球心，1 为半径，画不同几何距离的等位球，图2 给出了不同距离度量的等位球结果. 从图2的结果可以看出，不同几何距离度量的等位球的形状不尽相同，除了欧氏距离的等位球是标准圆球外，其余几何距离度量的等位球均不是圆球，其球面是类三角形的形状，这也说明不同的几何距离度量所反映出的流形几何结构均不同.

图2 不同几何度量的等位球

3.2 几何中值

数据的中值通常可用作数据的代表，表示了数据的某种属性. 对于一组m个正实数{x1，x2，…，xm}，其中值xmed是此m个正实数排序后的中间数，在数学上，中值是如下最小值问题的解：

其中，|x-xi|是x与xi之间的距离. 从式（15）可知，中值是到此m个正实数的距离和最小的数.

与实数的中值定义类似，对于矩阵流形上的一个矩阵集，其几何中值是到此矩阵集的几何距离之和最小的矩阵，其定义如下：

定义5对于给定的矩阵{R1，R2，…，Rm}，其几何均值是下式的最小值问题的解：

对于不同的几何距离，根据式（16），可以得出不同的几何中值，下面的推论给出了不同几何距离度量对应的中值.

推论1对于一组矩阵{R1，R2，…，Rm}，其AIRM 中值为如下迭代式［42］：

推论2对于一组矩阵{R1，R2，…，Rm}，其LEM 中值为如下迭代式［43］：

推论3对于一组矩阵{R1，R2，…，Rm}，其KLD 中值为如下迭代式［18］：

推论4对于一组矩阵{R1，R2，…，Rm}，其SKLD 中值为如下迭代式：

其中，P和Q分别为

证明假设函数F(R)为

其梯度可计算为

令∇F(R) =0，式（23）可化为类似于代数里奇方程，

解上述方程即可得证. 证毕

推论5对于一组矩阵{R1，R2，…，Rm}，其JBLD 中值为如下迭代式［44］：

上述推论中，下标t表示迭代次数，推论1 中的ε表示迭代步长.

4 度量的区分能力描述子

几何距离可度量流形上两点间的距离长短，更确切地说，几何距离度量了两点间局部几何结构差异性大小. 对于流形上的两点，利用某种距离度量其间的距离大小，距离越大，表明两点间的局部几何结构差异性越大，其间的区分度越大. 然而，对于给定的两点，不同的几何距离所度量出的距离大小不同，由于不同的几何距离的量纲不同，无法根据距离大小来判断哪种度量所度量出的局部几何结构差异性大或小，即其区分度大或小. 根据上述分析可知，不同的几何距离所反映出的流形几何结构不同. 一般认为，对于给定的两点，不同的几何距离所度量出两点间的局部几何结构差异性大小不同，即不同的度量对于给定两点的区分能力不一样. 为了衡量不同几何度量所度量出几何结构的差异性大小，本文首先定义出一个能表征流形上某点处的局部几何结构描述量，即各向异性因子（Anisotropy Index，AI），然后，基于AI 定义区分能力描述子.

定义6对于矩阵流形P(n)上的任意一点P，其对应的AI大小可由下式计算：

从上式的定义可看出，AP的大小反映的是点P到欧式空间{αI，α＞0}的投影距离的平方，AP的值越大，即点P到欧式空间{αI，α＞0}的投影距离越大，点P处的各向异性越强. 此外，AP与所采用的几何距离相关，不同的几何距离所定义出的各向异性大小不同，基于不同的几何距离，下面推论给出了各向异性因子的计算方式.

推论6对于矩阵流形P(n)上的任意一点P，AIRM对应的AI大小为

证明 ∀α＞0，有

使式（28）等于0，则有

证毕

推论7对于矩阵流形P(n)上的任意一点P，LEM对应的AI大小为

证明∀α ＞ 0，有

使上式等于0，则得证. 证毕

推论8对于矩阵流形P(n)上的任意一点P，KLD对应的AI大小为

证明 ∀α＞0，有下式

使上式等于0，则得证. 证毕

推论9对于矩阵流形P(n)上的任意一点P，SKLD对应的AI大小为

证明 ∀α＞0，有

上式等于0，即可得证. 证毕

推论10对于矩阵流形P(n)上的任意一点P，JBLD对应的AI大小为

其中，λi是矩阵P的第i个特征值.

证明∀α＞0，有

设{λ1，λ2，…，λn}是矩阵P的n个特征值，上式可表达为

上式可通过梯度下降法求解，即可得证. 证毕

对于矩阵流形上的两点P1和P2，AP1和AP2的大小差异则反映出两点间局部几何结构的差异，由于AP的大小与度量的量纲有关，为了消除量纲的影响，下面给出了区分能力描述子的定义.

定义7对于矩阵流形(n)上的任意两点P1和P2，其对应的区分能力描述子可由下式给出：

上式取两点处AI之商，可以有效消除量纲的影响.区分能力描述子的值L(P1，P2)越大，则表示度量对点P1和P2之间的区分能力越强.

5 实验结果与分析

为了全面验证算法的性能，本文设计相应的仿真实验来验证以下4方面：

（1）几何中值对干扰和样本数的鲁棒性；

（2）仿真数据下不同几何度量的区分能力的差异；

（3）小样本、非均匀杂波下矩阵信息几何检测器的性能优势；

（4）不同的特征以及不同的矩阵结构下检测性能的差异.

5.1 几何中值的鲁棒性分析

为了分析几何中值对干扰和样本数的鲁棒性，比较了几何中值与样本协方差矩阵的结果. 样本数据通过零均值多元复高斯分布产生，仿真产生40 个样本数据，分别在样本数据中随机加入1～15个干扰，干扰的归一化频率为0.22，干扰的信杂比为10 dB，根据式（8）将每一个样本数据建模为一个正定矩阵，分别计算加入干扰前后的几何中值，计算干扰对几何中值的影响大小，假设加入干扰前的几何中值为R0，加入干扰后的几何中值为Rinterf，则干扰对几何中值的影响大小如下式：

图3 给出了不同干扰数下影响大小值Lerror的变化情况，从结果可以看出，在不同干扰数下，干扰对SCM的影响大小Lerror大于几何中值，这说明几何中值对干扰的鲁棒性要好于SCM. 同时可以看出，在5 种几何中值中，干扰对AIRM 和LEM、KLD 和SKLD 的影响比较接近，对比干扰对几何中值的影响可知，干扰对JBLD的影响最小，其次是AIRM 和LEM，干扰对KLD 和SKLD的影响最大.

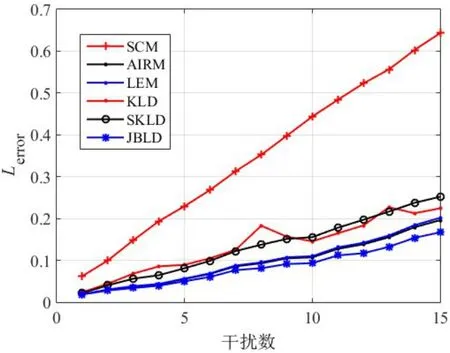
图3 不同干扰数对几何中值的影响

为了验证几何中值对样本数的鲁棒性，分别计算样本数为5～30时的几何中值，并与真实矩阵进行比较，计算不同样本数下几何中值相对于真实矩阵的差异大小. 图4 给出了不同样本数下几何中值的误差影响大小，从图中结果可以看出，样本数对SCM 的影响大于对几何中值的影响，此外，在5 种几何中值中，样本数对KLD 的影响最小，其次是SKLD，对AIRM、LEM 以及JBLD的影响比较接近.

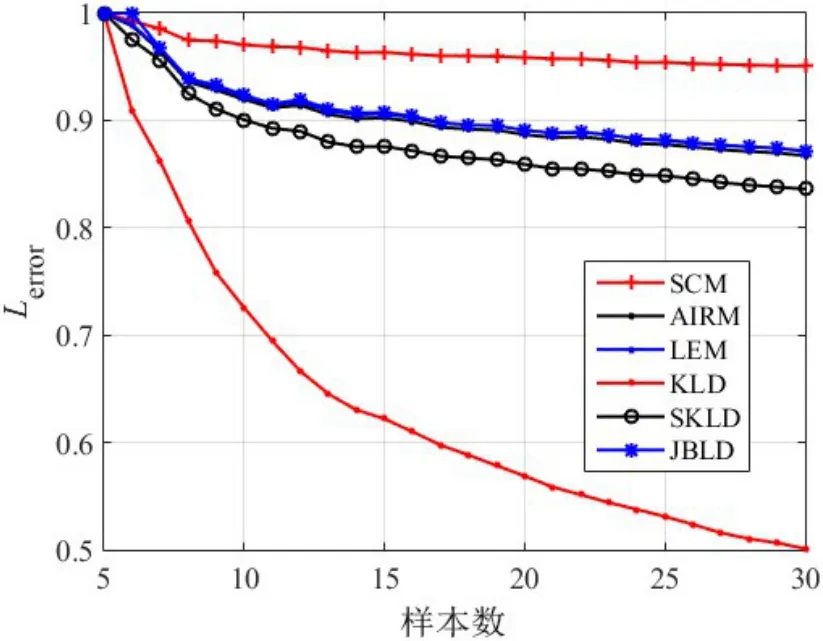
图4 不同样本数对几何中值的影响

5.2 度量的区分能力差异分析

为了分析不同几何度量的区分能力的差异，随机产生一组K=8 个样本的数据集，样本数据服从高斯分布，根据式（8）计算对应的正定矩阵，计算其几何中值矩阵Rg. 随机产生一个样本数据，在样本数据中加入归一化频率为0.2 的目标信号，目标信号的信杂比为18 dB，依据式（8）计算其对应的正定矩阵RD，基于不同的几何度量，通过式（39）计算区分能力描述子的值L(RD，Rg)，比较不同几何度量对应L(RD，Rg)的大小.

图5 给出了100 次蒙特卡洛实验下不同几何度量对应的L(RD，Rg)平均值结果，从结果可以看出，在信杂比为18 dB，K=N时，不同几何度量对应的区分能力不同，其中，KLD的区分能力最好，其次是JBLD，AIRM、LEM和SKLD三者的区分能力相近.

图5 不同几何度量的区分能力

5.3 检测性能分析

为了分析矩阵信息几何检测器的性能优势，在高斯和非高斯杂波下分析矩阵信息几何检测器检测性能，并与AMF 进行对比，分别比较了K=n、K=1.5n和K=2n的检测性能. 非高斯杂波是在高斯样本前乘上一个服从尺度参数为1 且形状参数为3 的Gamma 分布随机变量来获取，在辅助样本数据中随机加入了2个信杂比为20 dB 的干扰，其归一化频率为0.2，利用辅助样本数据计算几何中值矩阵，比较几何中值矩阵与待检测样本对应矩阵之间的几何距离与检测门限的大小，大于门限，表示存在目标信号，反之亦然，检测概率通过1 000 次蒙特卡洛仿真实验得到，虚警概率设定为PFA=10-3，检测门限根据100/PFA次蒙特卡洛仿真实验得到，图6给出了高斯和非高斯杂波下不同信杂比对应的检测概率曲线.

从图6 的结果可以看出，当K=n时，由于样本数较少，AMF 的检测性能较差，而矩阵信息几何检测器的性能较好；当K=1.5n时，杂波协方差矩阵的估计性能损失较大，高斯杂波下矩阵信息几何检测器的性能明显好于AMF，而非高斯杂波下，矩阵信息几何检测器的性能稍好于AMF；而当K=2n时，高斯杂波下矩阵信息几何检测器的性能仍然明显好于AMF，而在非高斯杂波下，AMF 的检测性能好于矩阵信息几何检测器. 这说明，在高斯杂波下，矩阵信息几何检测器的性能明显优于AMF，而在非高斯杂波下，只有当K＜2n时，矩阵信息几何检测器的性能才具有优势.

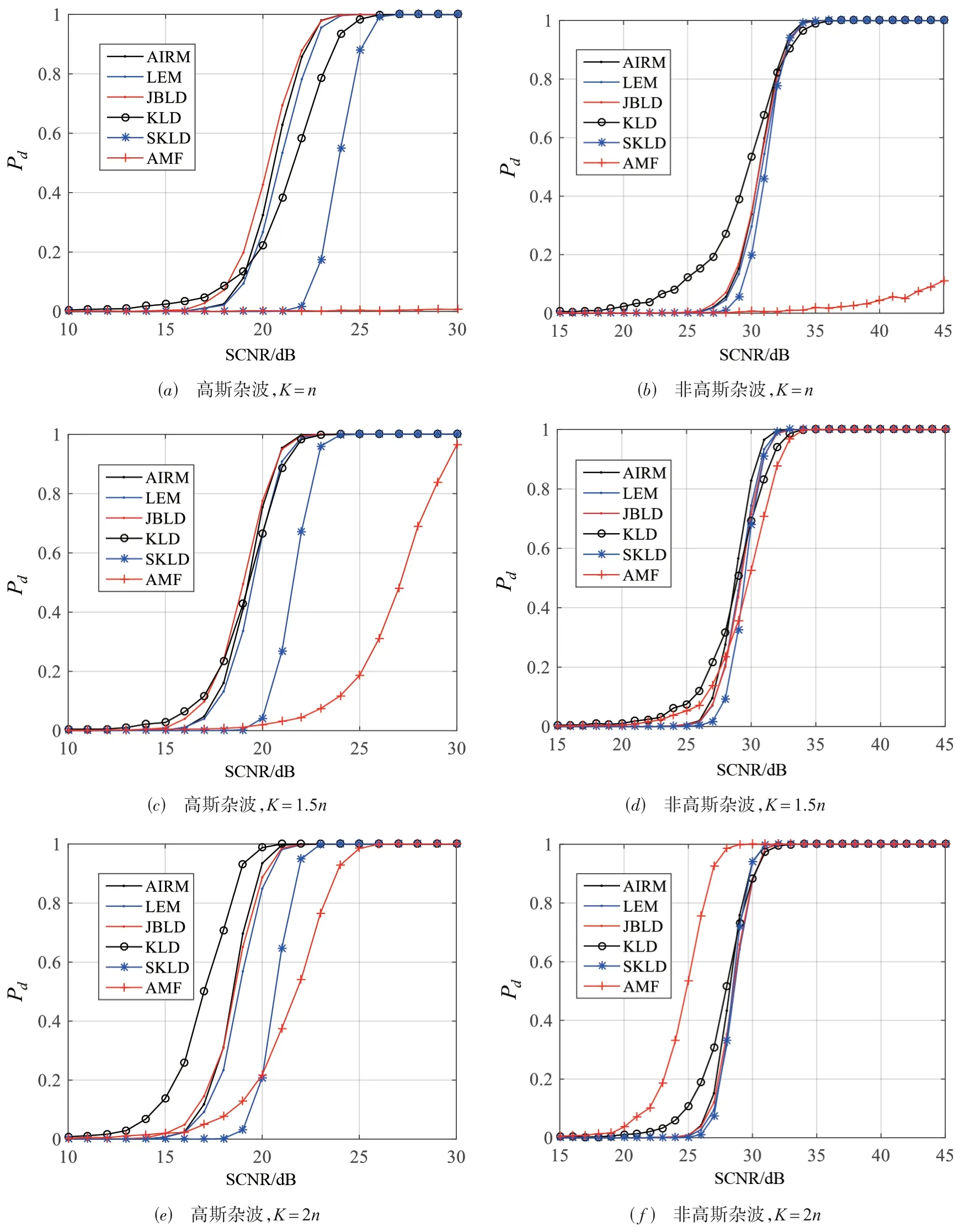
图6 高斯与非高斯杂波下不同信杂比下的检测性能

在5 种矩阵信息几何检测器中，SKLD 检测性能在高斯和非高斯杂波下均最差. 在高斯杂波下，KLD的检测性能随着样本数的增加变化最大，AIRM、LEM 和JBLD的检测性能较为接近；而在非高斯杂波下，几种检测器的性能均比较接近，KLD 的检测性能在低信杂比下有优势，SKLD 稍差于AIRM、LEM 和JBLD 的检测性能.

5.4 不同特征和矩阵结构下检测性能的差异分析

为了分析不同特征和矩阵结构对检测性能的影响，考虑到算法的效率，选择KLD 检测器作为研究对象，其他几何度量可利用类似的方法进行对比. 实验中考虑到2 种特征，分别是自相关特征和AR 谱的相关系数特征，2 种特征均表征了信号的相关特性，但自相关特征是从时域出发的信号相关性，而AR 谱系数特性表示了信号频域对应的相关特性，不同的特征对目标信号和杂波的区分性不同. 不同的矩阵结构描述了矩阵流形不同的局部几何结构，使得流形上两点之间的可分性也不一样. 基于2种相关性特征，比较KLD 检测器的性能差异，同时，针对AR 谱相关性，分别用式（8）和式（9）建立正定矩阵模型，比较KLD 检测器的性能差异.

图7 给出了不同特征和矩阵结构下KLD 检测器性能的对比结果. 从图7 的结果可以看出，不同特征和矩阵结构下KLD 检测器的性能有差异，对于ARCorrToplitz和ARCorrDialog 方法，两者均采用AR谱相关特征，但矩阵结构不同，ARCorrToplitz 采用的是式（8）矩阵结构，而ARCorrDialog 采用的是式（9）矩阵结构. 从实验结果可以看出，式（9）的矩阵结构对应KLD 的检测性能好于式（8）的矩阵结构，这说明，不同矩阵对应的检测器性能有差异，对于CorrDialog和ARCorrDialog方法，两者矩阵结构相同，均采用式（9）的矩阵结构，但相关特征不同，CorrDialog 利用的是时域相关特性，ARCorrDialog 利用的是AR 谱相关特性. 从实验结果可以看出，信号的时域相关性特征对应的KLD 检测器性能好于频域相关性特征，这说明，不同的特征对应的检测器性能有差异. 针对不同的检测背景，提取出合适的信号特征，探索合适的矩阵结构，对提升矩阵信息几何检测器的性能具有重要意义.

图7 不同特征和矩阵结构下KLD的检测性能

6 总结与展望

本文提出了一种新的信号检测器框架，即矩阵信息几何中值检测器，该检测器将信号检测问题转化为矩阵流形上的几何问题，将从样本数据中提取出的特征建模为一个正定矩阵，在矩阵流形上可采用不同的几何度量来区分目标信号与杂波之间的差异性，从而实现信号检测，实验证明，该检测器在小样本、非均匀杂波下具有明显的性能优势，此外，系统分析了检测器对干扰以及样本数的鲁棒性和不同特征与矩阵结构下检测性能的差异.

基于矩阵信息几何理论与检测器原理，结合矩阵分析理论，本文指出了该检测器在以下几方面值得进一步深入研究：

（1）不同检测背景下杂波特性不同，提取出合适的特征，可有效提升目标与杂波间的区分性，深入研究杂波的形成机理，从各层面分析杂波特性，提取出合适的特征是一个重要的研究内容；

（2）矩阵结构对特征的表征能力不同，同时，矩阵结构决定了矩阵流形的局部几何结构，不同的矩阵结构对目标和杂波的区分能力不同，研究合适的矩阵结构来表征特征是一个重要的问题；

（3）流形上不同的几何度量反映了不同的几何结构，对两点间的区分能力也不同，研究探索新的几何度量并提升目标与杂波在流形上的可分性是需要深入研究的一个关键问题.