基于符号定时偏差补偿的过零点采样自干扰消除

荆 楠，班容键，田立勤，王 林，刘 丰

（1. 燕山大学信息科学与工程学院，河北秦皇岛 066004；2. 华北科技学院河北省物联网监控工程技术研究中心，河北廊坊 065201；3. 河北省信息传输与信号处理重点实验室，河北秦皇岛 066004）

1 引言

带内全双工（Full Duplex，FD）是第五代移动通信技术（5G）实现频谱利用率倍增的关键技术之一. 与现有的频分双工、时分双工相比，FD使无线终端能够在同一频带上同时发送和接收信号来提高频谱效率. 而全双工的实施则必须要克服本地发射链路的发射信号对接收链路所造成的干扰，这个干扰被称为自干扰（Self-Interference，SI）信号. 由于发射链路与接收链路的距离要远小于接收链路与远端节点的距离，因此SI 功率比接收链路接收到来自远端节点的期望信号（Desired Signal，DS）功率高出接近100 dB，这使得接收链路接收到的DS 淹没在强大的SI 信号中，从而无法被正确解调［1，2］. 此外，SI 信号未经抑制直接送入接收链路数模转换器（Analog to Digital Converter，ADC），其功率超出ADC 的动态范围将造成ADC 过饱和. 因此，只有在接收链路进行SI消除才能真正实现全双工通信.

现有的方法通过三个步骤来完成SI消除：天线域，模拟域和数字域. 天线域通常采用特殊的天线设计实现SI消除，如天线间物理隔离［3］、天线极化［4］、单天线循环器［5］等方法，这些方法可实现25～40 dB 的SI 消除水平. 然而，经天线域消除后的SI 功率水平仍远大于DS接收功率，还需要在模拟域进一步消除. 常用的模拟域方法采用多抽头延迟线结构模拟多径信道，通过固定或者自适应方法调整每个抽头的增益和时延重构无线多径信道，进而获得SI 的估计值，然后，在接收信号中减去重构的SI 实现SI 消除. SI 在模拟域可实现30～60 dB 消除水平［6～8］. 经天线域和模拟域联合消除之后，SI 功率水平可降至接收链路ADC 动态范围之内，并与DS 功率水平相当. 随后，残余的SI随DS 一起通过ADC进入数字域进行解码解调. 为了实现DS 正确解调，还需要在数字域进一步消除残余SI. 现有的数字域消除方法有重构SI［9］、盲源分离［10］、独立分量分析［11］等方法，至少可以实现30 dB的自干扰消除性能.

天线域联合模拟域方法可提供高达100 dB 的自干扰消除，但这些方法需要复杂的硬件电路设计［6］. 即使简化硬件电路设计［12］或者采用多抽头参数的自适应算法［13］，硬件设备的非线性将会带来额外SI 残留，造成DS 无法正确解调［14，15］. 针对上述问题，研究人员提出［16］是否可以跳过模拟的硬件开销，仅使用数字域方法完全消除接收信号中的SI. 欲实现该目标所面临的挑战是如何解决SI功率过高导致ADC动态范围存在过饱和问题.

文献［16］是第一个尝试使用数字域信号采样方法来消除SI 的工作. 该方法设计一个辅助信号加入到接收信号中，然后在辅助信号与SI 两者之和信号的振幅电平为零的时刻对接收信号进行采样，这使得采样后的信号里只含有DS 而不再携带SI，从而实现自干扰消除. 该方法的关键是准确计算辅助信号与SI 之和信号的过零点，其准确计算的前提是系统完全同步. 然而，在实际通信系统中却存在收发不同步问题，其中包括符号定时偏差（Symbol Timing Offset，STO），其中STO 将导致SI 发生相位旋转，造成辅助信号与SI 之和的信号过零点计算不再准确.

针对系统存在STO 时文献［16］方法性能恶化问题，本文提出一种基于STO 补偿的信号过零点采样方法（Zero Crossing Sampling with STO Compensation，ZCSSTOC）. 首先，使用最小二乘（Least Squares，LS）信道估计方法重构一个理想的不包含系统STO 的SI 信号. 其次，利用该估计的SI 信号计算系统同步情况下的过零点集合. 然后，使用相关函数法和差值法估计系统当前的STO. 最后，根据该STO 的估计值对系统同步情况下的过零点集合进行补偿. 这样就得到系统存在STO 时的过零点集合.

2 信号模型

本文提出的基于过零点补偿的自干扰消除系统模型如图1 所示. 发射链路由正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）调制模块、数模转换器（Digital to Analog Converter，DAC）、功率放大器（Power Amplifier，PA）和发射天线组成. 接收链路由低噪声放大器（Low Noise Amplifier，LNA）、过零点补偿模块和过零点采样模块组成. 其中过零点补偿模块由信道估计模块、STO估计模块、SI重构模块、过零点计算模块和过零点修正模块组成. 过零点采样模块由ADC 与Nus-OFDM解调模块［17］组成.

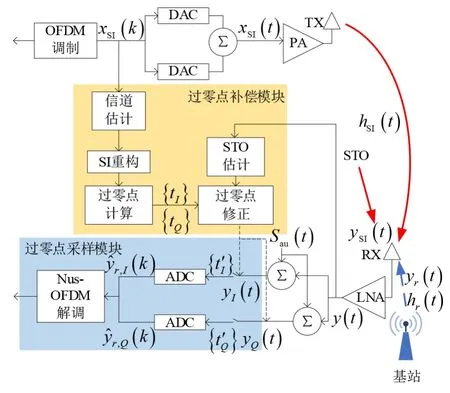
图1 基于ZCS-STOC双天线全双工自干扰消除系统模型

在发射链路，复基带信号xSI(k)经DAC 后转换为模拟信号xSI(t)，再经PA 放大后发射. 接收链路所接收到的信号y(t)由自干扰信号ySI(t)，期望信号yr(t)和噪声n(t)组成，其关系如式（1）所示：

其中，xr(t)为远端基站或移动台发射的期望信号，xSI(t)与xr(t)均为OFDM 信号，由2N个子载波组成，频率均匀分布在f-N+1=( -N+1) /T′与fN-1=(N-1) /T′之间，T′为一个OFDM 符号时间，其中T′=TCP+T，TCP表示循环前缀的长度，T表示OFDM 符号内数据长度.hSI(t)和hr(t)分别表示SI和DS多径传播信道的冲激响应. 过零点采样的核心思想是接收端在ySI(t)幅值为零的位置对y(t)进行采样，这使得采样后的结果中将不再含有ySI(t). 然而，在ySI(t)过零点位置对y(t)进行采样所得到的采样点数将小于2N，根据奈奎斯特采样定律可知，采样点数不足2N将造成yr(t)解调失真. 为了解决上述问题，需设计一个辅助信号以使ySI(t)过零点数量增加至2N，标记辅助信号为Sau(t).

在接收天线处，y(t)被分为同相分量（In-phase，I）和正交分量（Quadrature，Q）两路，分别用{y(t)}和ℑ{y(t)}来表示.ℜ{y(t)}和{y(t)}分别加入辅助信号Sau(t)后［16］，其相应的同相信号yI(t)和正交信号yQ(t)可表示为

其中，辅助信号数学表达式由文献［16］给出

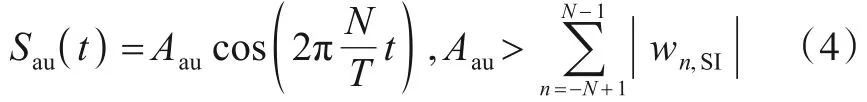
其中，Aau为幅值，wn，SI为ySI(t) =傅立叶级数展开系数. 将式（1）代入式（2）和（3），得到：

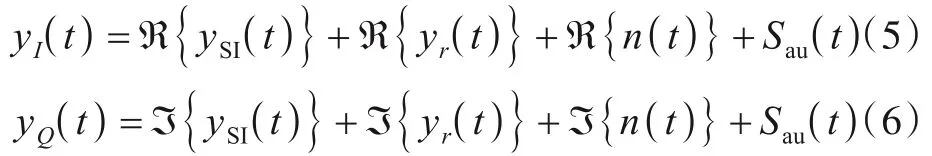
令ySI(t) +Sau(t)过零点采样时刻集合为：

其中，tI，i和tQ，i，i=1，…，2N表示集合内的过零点采样时刻.采用tI与tQ对yI(t)和yQ(t)进行采样，得到：

其中，(t)和(t)是yI(t)和yQ(t)经tI与tQ采样后的离散信号，tI与tQ可由方程式（11）和式（12）求出：

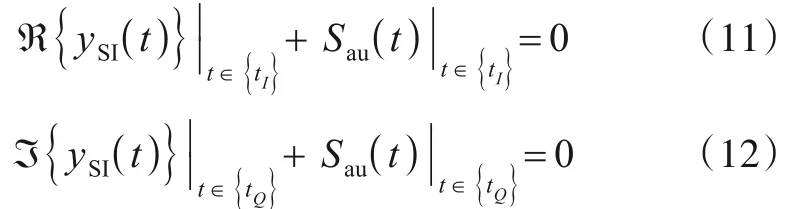
通过式（9）～（12）可以看出，只要能准确计算tI与tQ，就可以完全消除ySI对yr(t)的影响. 然而，式（9）～（12）成立的前提是假设系统完全同步. 事实上，实际通信系统存在同步偏差，其中包括符号定时偏差. 符号定时偏差的存在使原本采样时刻超前或滞后一段时间，此时若仍按照tI与tQ对yI和yQ进行采样，式（9）～（12）将不再成立，采样后的信号yI(t)和yQ(t)将包含SI以及额外引入的Sau(t)，进而无法实现SI消除.

定义系统的符号定时偏差为tSTO，图2 直观地说明tSTO对ySI(t) +Sau(t)过零点计算的影响. 令ySI(t) +Sau(t) =y′SI(t)，y′SI(t)与DS 的幅值与采样点分布如图2所示. 为了方便问题讨论，SI 与DS 均为功率相等且没有信道和噪声失真影响的OFDM 信号，子载波数为8，调制方式均为正交相移键控（Quadrature Phase Shift Keying，QPSK）. 图2（a）为无tSTO影响的情况，以采样点集合tI与tQ对yI(t)和yQ(t)进行采样，由式（11）和（12）可知y′SI(t) =0，采样结果中仅包含DS 而不存在SI 进而实现了SI 消除. 然而，SI 在传播过程中经历tSTO后，y′SI(t)过零点位置将发生变化. 如果仍按照tI与tQ对yI(t)和yQ(t)进行采样，采样结果中y′SI(t) ≠0，式（11）和（12）将不再成立，如图2（b）所示.

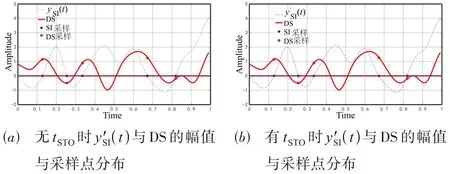
图2y′SI(t)与DS的幅值与采样点分布

因此，本文设计一种基于tSTO补偿的过零点采样时刻计算方法，如图1 中过零点补偿模块所示. 首先从发送链路引出一个OFDM 调制信号送入信道估计模块得到自干扰信道的估计值SI(t)，其次，通过SI(t)得到SI的重构信号SI(t). 此时得到的SI(t)是未通过多径传播的SI 估计值，不包含系统符号定时偏差，因此，将SI(t)代入式（11）和（12）便可得到系统同步情况下的采样时刻集合tI与tQ. 然后，接收链路从y(t)中耦合一路信号送入STO 估计模块得到系统当前的符号定时偏差STO. 最后，利用STO对集合tI，tQ中的每个采样时刻进行纠正，得到新的采样时刻集合. 新的采样时刻集合，其定义如下：

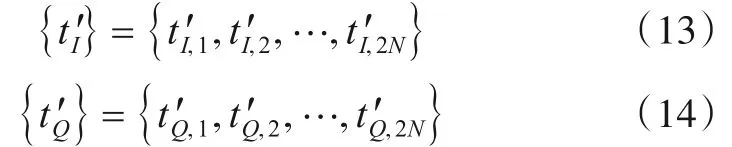
其中，t′I，i=tI，i-tSTO，t′Q，i=tQ，i-tSTO，i=1，…，2N.

利用式（13）和（14）给出的过零点采样时刻集合对yI(t)和yQ(t)进行采样，则系统即使存在tSTO情况下式（9）～（12）仍然成立，即

3 非均匀采样时刻计算

3.1 STO引起的采样偏差

令s(t)是一个周期为T的连续基带信号，其傅里叶级数可表示为

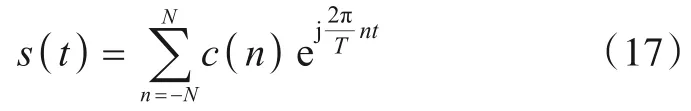
其中，c(n)表示傅里叶级数系数，2N表示与子载波个数相同的谐波. 按照式（17）可以得到SI 同相分量ℜ{y(t)}与正交分量ℑ{y(t)}的傅里叶级数展开分别为

根据OFDM 符号有效数据起始点位置的不同，存在两种符号定时偏差，如图3 所示，分别指的是接收OFDM 符号有效数据部分的起始点相对于定时准确时刻分别为超前和滞后两种情况. 令CP 为截取OFDM 符号尾部的四分之一，δ为估计OFDM 符号的起始点与准确的定时相差的子载波宽度，其与tSTO的关系可表示为

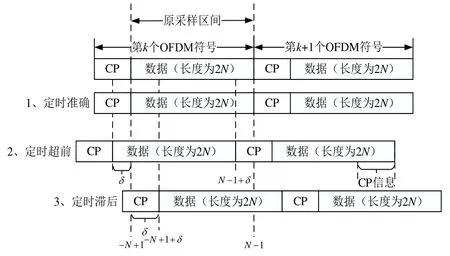
图3 两种符号定时偏差

其中，δ=0 表示定时准确，δ＜0 表示定时超前，符号与定时准确相比向左移δ，δ＞0 表示定时滞后，即符号与定时准确相比向右移δ.

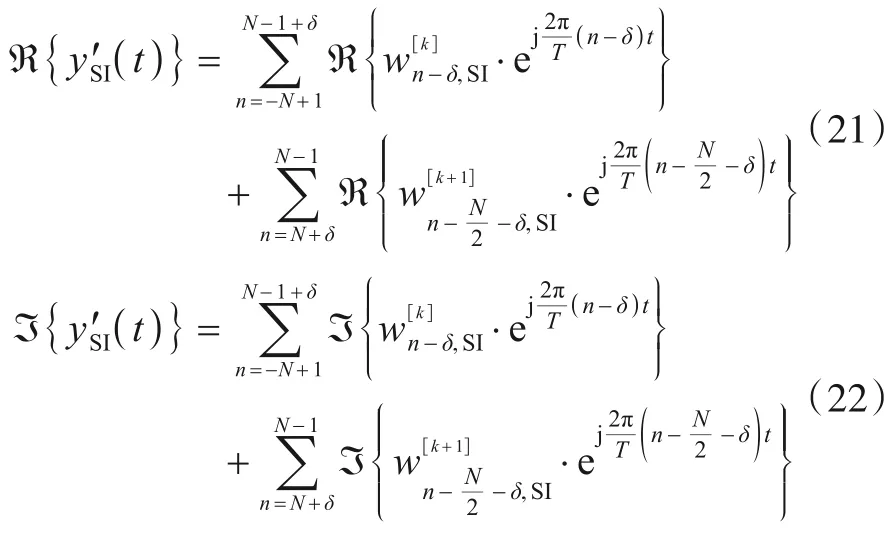
定时超前为OFDM 符号有效数据起始点位于同步定时时刻之前的情况. 若系统存在定时超前符号定时偏差，若不进行STO 补偿对接收信号进行过零点采样，此时SI 同相分量ℜ{y′SI(t)}与正交分量ℑ{y′SI(t)}分别为其中，分别为图3中第k+1个OFDM 符号离散傅里叶级数展开系数. 由式（21）和（22）可以看出，公式右侧第一部分为留在采样区间内的原OFDM 符号的部分数据，第二部分为由于tSTO引起的第k+1 个OFDM 符号的部分CP 数据，可由第k+1 个OFDM 符号数据尾部相对应部分获得. 因此，由式（21）与式（22）可知，tSTO引起的循环移位造成原采样区间内，第k个OFDM 符号丢失部分数据，同时混入第k+1 个OFDM 符号数据，进而破坏掉原采样区间内SI信号的过零点位置.

图3 中定时滞后为OFDM 符号的有效数据起始点位于定时同步时刻之后的情况. 受定时滞后影响，SI的同相分量ℜ{y″SI(t)}与正交分量ℑ{y″SI(t)}分别可写为

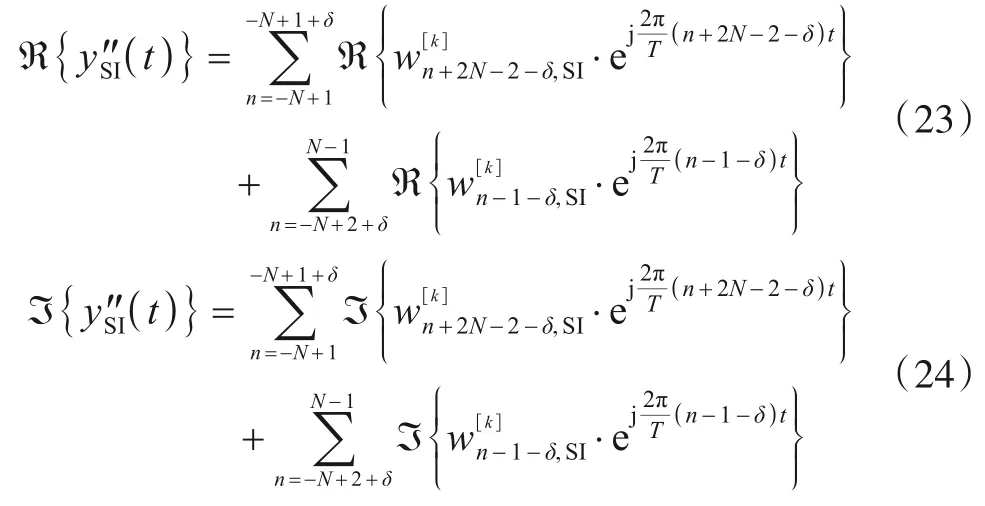
由式（23）和（24）可以看出，公式右侧的第一部分为tSTO造成的第k个OFDM 符号部分CP进入采样区间.由于CP 是重复OFDM 符号尾部四分之一数据，因此定时滞后的情况也可以看作为OFDM 符号发生循环移位，即第k个OFDM 符号尾部长度为δ的数据部分移位到起始位置，这使得整个OFDM 符号的起始位置发生变化. 公式右侧第二部分为原第k个OFDM 符号留在采样区间内的部分数据. 由于tSTO的存在，虽然未发生循环移位数据部分的傅立叶级数系数没有改变，但是级数的起始位置与式（18）和式（19）相比发生移位.

由式（21）～（24）讨论可知，若对系统存在的符号定时偏差不予补偿，SI 信号将发生相位旋转，同时其频谱系数也将发生改变. 若仍然按照tI与tQ对接收信号进行采样，将产生采样偏差进而无法消除SI信号.

3.2 STO估计

CP 是OFDM 符号尾部四分之一的副本，文献［18］利用CP与OFDM尾部数据部分相同这一特征提出采用差值法［19］和相关函数法［20］对tSTO进行估计. 插值法和相关函数法均设定两个滑动窗口W1 和W2，如图4 所示，两者间隔2N个子载波宽度. W1 与W2 均以δ为单位同时向左或者向右滑动，W1 与W2 每滑动一个δ，插值法和相关函数法均计算一次两个窗内信号采样点的相似度，相似度最高的δ即为系统当前的tSTO.

图4 基于CP的STO估计技术

具体来讲，ySI表示W1 窗中的采样点，表示W2 窗中相同位置的采样点. 差值法通过求W1 与W2 中ySI的差来计算相似度，然后将所有差值求和，可见差值越小代表W1 与W2 的相似度越大. 这个最小值所对应的δ即为系统当前的tSTO，其计算公式如下：

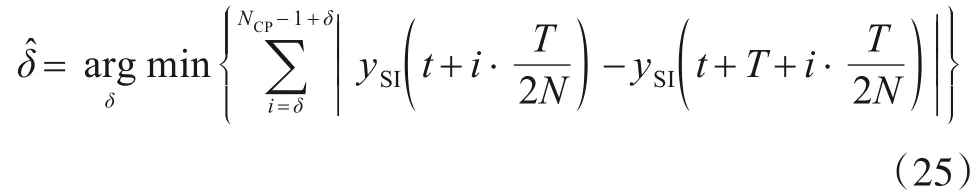
相关函数法则是通过计算W1 与W2 中ySI的相关度，然后将所有相关度求和，这个和越大W1 与W2 相似度越大. 因此，这个W1 与W2 相似度达到最大值所对应的δ即为系统当前的tSTO，其计算公式如下：

差值法和相关函数法对STO 进行估算也存在STO补偿误差. 首先，ADC电路对y(t)进行采样时将存在少量数据丢失. 其次，δ不能过度偏移，其偏移量具体受限于无线信道脉冲响应的最大时延扩展，如图5 所示. 假设信道最大时延扩展为τmax，若δ位于区域A，此时第k个OFDM 符号的FFT 窗未进入第k－1 个OFDM 符号多径扩展区域，即不存在符号间干扰，则差值法和相关函数法具有较好的估计性能. 若δ位于区域B，则第k个OFDM 符号的FFT 窗与第k－1 个OFDM 符号或第k＋1个OFDM 符号发生混叠，发生符号间干扰，此时采用差值法和相关函数法对系统STO 的补偿效果将严重下降.

图5 STO补偿误差产生原因

3.3 过零点采样时刻计算

由图1中过零点补偿模块可知，本文首先利用发送链路产生的基带信号，采用LS信道估计方法得到不存在tSTO情况下的SI 信道估计值SI[k]［21］，然后根据SI[k]计算SI信号估计值SI[k]. 由于不考虑tSTO并且收发天线相距较近，有理由认为SI 传播为直视传播（Light of Sight，LOS），因此，本文认为SI[k]就是理想SI 信道，SI[k]就是理想的SI，即SI[k] ≈HSI[k] ，SI[k] ≈YSI[k]，其中SI[k]和SI[k]分别为SI(t)和SI(t)的离散傅里叶变换.

其次，将SI 重构模块得到的SI(t)代入式（11）和（12），根据求根算法［22］计算得出系统完全同步情况下过零点集合tI和tQ.

最后，根据STO 估计模块得到的STO对tI和tQ中的每一个过零点进行补偿，进而得到当前系统存在符号定时偏差情况下的非均匀采样时刻集合t′I和t′Q，即t′I和t′Q满足如下等式：

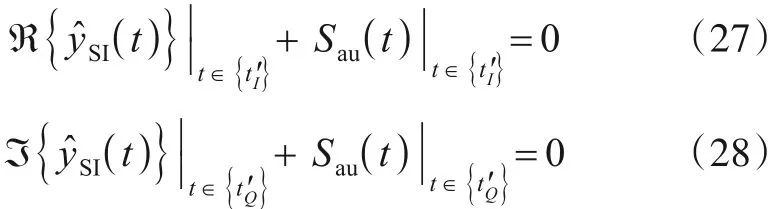
将式（27）和式（28）中ℜ{SI(t)}和ℑ{SI(t)}展开成傅里叶级数：

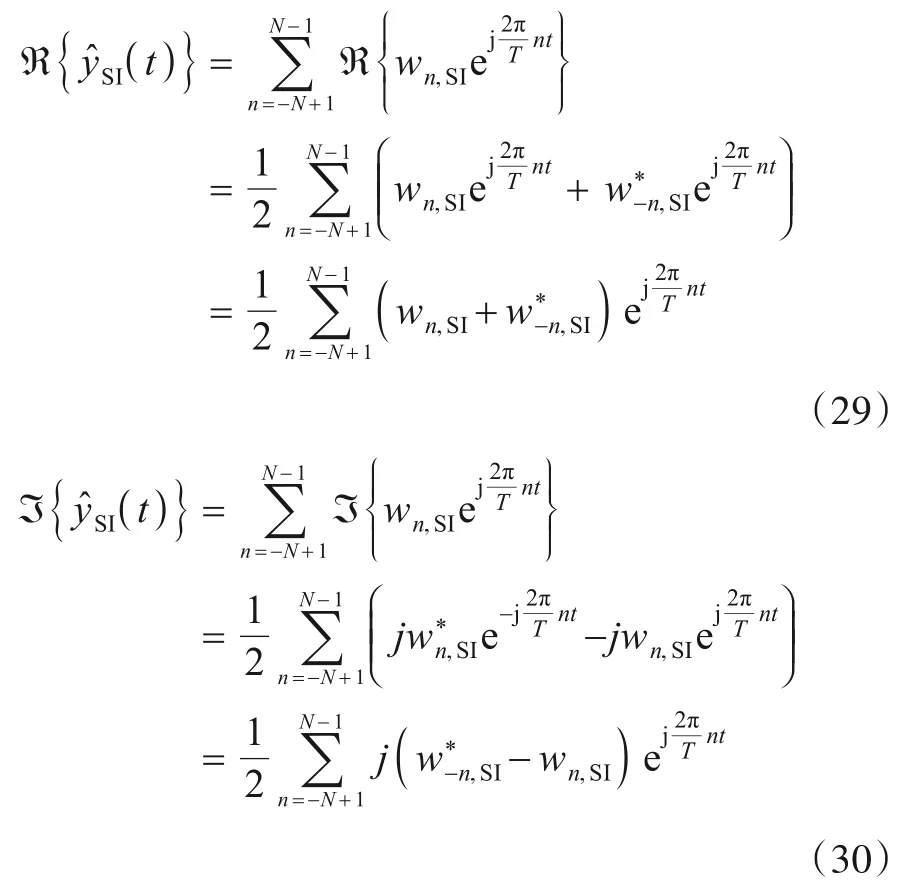
文献［16］指出式（29），式（30）是自逆多项式，存在过零点. 但是，其过零点不能保证一定分布在单位圆上，且数量也不足2N个. 因此，需在SI(t)基础上增加辅助信号，以使式（29）（30）满足自逆多项式有2N个零点位于单位圆上的条件：

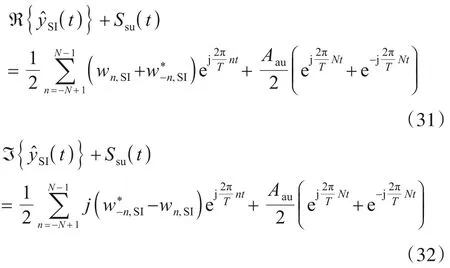
根据式（27）和（28）对（31）和（32）进行采样：

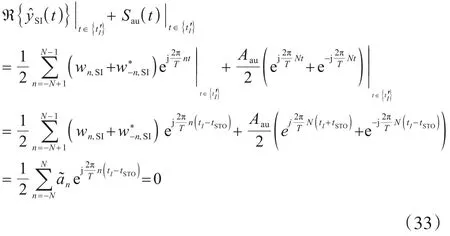
综上，系数和为

4 性能测试与分析

4.1 仿真参数设置

影响本文所提出方法ZCS-STOC 性能的因素就是计算t′I和t′Q的准确性，其与SI(t)估计的准确性有关，同时也受tSTO估计准确性的影响. 因此，本文将从信道估计的自干扰抑制性能，导频数量，的不同计算方法三个方面对ZCS-STOC性能进行评价.

自干扰消除能力（Self-Interference Cancellation Capability，SICC）是全双工自干扰消除性能测试中最直观的评价标准，直接以消除SI的能力作为评价标准，可以定义为

信号干扰比（Signal to Interference Ratio，SIR）代表着DS 与SI 的接收功率的差异，可以更加直观地说明不同SI接收功率对于系统性能的影响，可以表示为

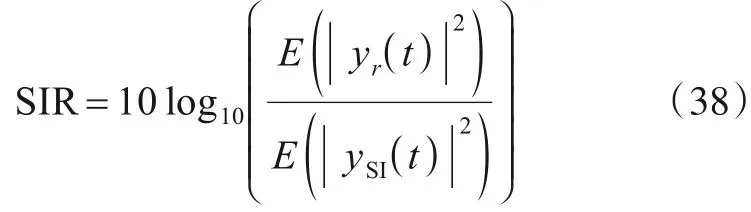
本文采用的仿真参数如表1所示.

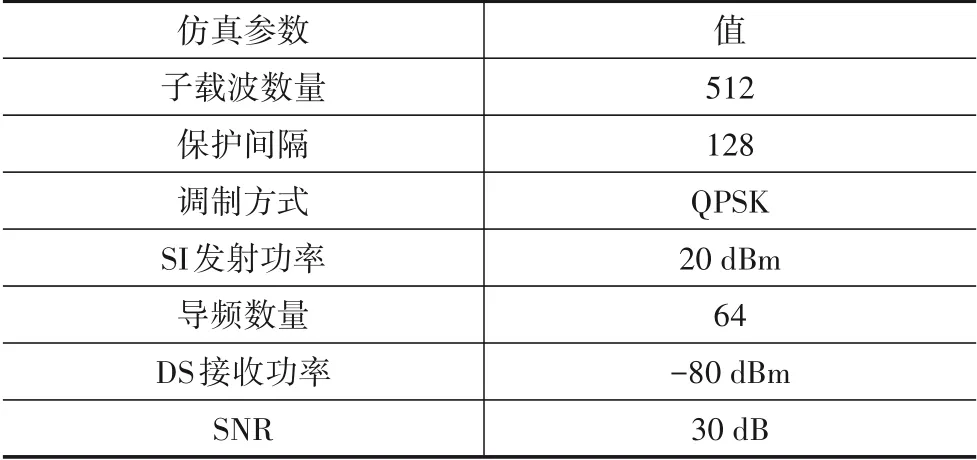
表1 OFDM仿真系统参数

此外，为进一步验证所提出方法的有效性，本文的实验结果将与文献［16］所提出方法进行对比.

4.2 ZCS-STOC性能测试

图6 给出本文提出ZCS-STOC 方法与文献［16］的AS（Advanced Sampling）方法在不同tSTO情况下的SICC对比. 图6 中tSTO的影响采用δ来评价，并使用差值法对δ估计，令δ=-1，δ=2 分别表示起始点超前1 个子载波宽度与滞后2 个子载波宽度，分别对应图3 中的情况2与情况3.

如图6所示，AS方法在tSTO与定时时刻相差一个子载波时，其SI 消除水平为55 dB，然而tSTO仅增加1 个子载波宽度，其SI消除性能急剧下降，仅为25 dB，不再能有效消除SI. 这说明AS方法在系统存在tSTO时，将无法再实现SI 消除. 与之相比，本文提出的ZCS-STOC 方法，在δ=-1 与δ=2 两种情况下的SICC 均可以达到80 dB 以上，这说明通过对tSTO进行补偿，ZCS-STOC 方法在系统存在tSTO时仍然可以有效消除SI. 由图6 还可以看出，虽然SI信号功率值不断减小，SIR 由小变大，但是ZCS-STOC 方法的SI 消除性能仍稳定在80 dB，并未发生剧烈变化，这说明SI信号功率水平对ZCS-STOC 方法影响较小.

图6 ZCS-STOC方法与AS方法SICC对比曲线图

图7 说明ZCS-STOC 方法性能受不同tSTO估计方法的影响. 本文采用差值法（Difference Method，DM）与相关函数法（Correlation Function Method，CFM）两种不同tSTO估计方法评价ZCS-STOC方法的SI消除性能. 当δ=2 时，采用相关函数法的ZCS-STOC 能实现77 dB 的SICC，其性能比采用差值法的ZCS-STOC 小6 dB. 然而，相比于AS方法仍然有约55 dB的性能提升.

图7 两种不同STO估计方法对比曲线图

然而，若tSTO的值大幅增加，tSTO无法得到充分补偿，这将造成本文所提方法性能下降，如图8所示. 图8给出δ在（-100，100）范围内变化时，本文所提方法与AS方法性能对比曲线.AS方法的性能从δ≠0开始便急剧下降，而本文所提方法虽然在δ大幅增加后其性能有所下降，但是在-45 ＜δ＜45 范围内，仍可以达到70 dB以上SI消除性能.

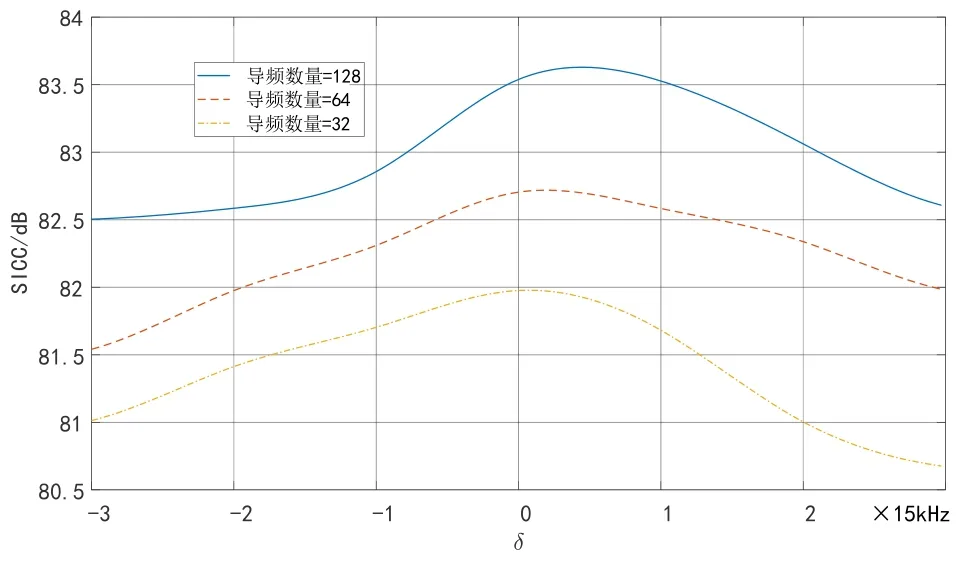
图8 不同tSTO下的SICC曲线

本文采用LS算法重构SI信道，而LS信道估计的准确性与导频数量密切相关. 图9 分别给出导频数量分别为128，64，32 三种情况下的ZCS-STOC 方法SICC 性能曲线. 从图中可以看出，随着导频数量的增加，SICC逐渐提升，这是因为导频数量越多，重构SI越准确，t′I和t′Q也将更加精准.

图9 不同导频数量对SICC影响曲线

图10 评价接收信号中的噪声对ZCS-STOC 方法性能的影响. 本文使用SNR 作为衡量噪声大小指标. 如图10所示，随着SNR增加，噪声功率降低，ZCS-STOC曲线非常稳定，没有随着SNR 的变化而变化，这说明ZCSSTOC方法具有较好的抗噪性能.

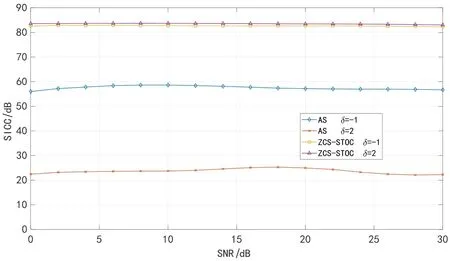
图10 不同SNR下的SICC曲线

5 结论

OFDM 系统收发链路之间存在的符号定时偏差严重影响自干扰过零点采样方法的自干扰消除性能. 针对上述问题，本文提出一种STO 补偿的过零点采样时刻计算方法. 该方法首先估计STO，并根据该STO 估计值对SI 过零点时刻就行校正，然后基于校正后的过零点集合对接收信号进行采样，从而完成SI信号消除. 仿真结果表明，本文提出方法在系统存在STO 时仍然可实现83 dB自干扰消除水平.