两类构造阿基米德Copula 生成元的方法
余 欣,吕王勇,杨和柳,张琼文
(四川师范大学数学科学学院, 四川 成都 610068)
1 引言
熟知,Copula 是将多维的联合分布函数和一维的边缘分布函数连接在一起的一个二元函数.1999 年Nelsen[1]对Copula 函数的含义和性质做了全面详细的介绍,后来,随着理论的逐渐完善,Copula 函数在金融市场股市之间的信息流动、相依性分析以及金融风险管理等方面得到了广泛应用[2-5].迄今为止,国内外学者对Copula 理论做了大量的研究工作并且取得了较好的研究成果.
在众多的Copula 函数族中,阿基米德Copula 函数族由于构造方便、计算简单,具有一般Copula 函数所不具有的较好的性质而在金融领域得到广泛应用.目前国内外对阿基米德Copula 的研究已有一定成果,最早关于阿基米德Copula 模型的相依结构和序关系的文章源于Nelsen 的研究[6],随后,利用阿基米德Copula 对投资分配组合及其风险进行了研究[7-10].阿基米德Copula 是由一些单调递减的凸函数所生成的一类Copula,这类单调递减的凸函数称为“生成元”,只要找到所谓的“生成元”,就能实现这一类Copula 的构造.该文的主要工作是讨论阿基米德Copula 生成元的构造,到目前为止,构造生成元主要是从函数和变换两个角度讨论.阿基米德Copula生成元常见的构造方法有:Laplace 变换法[11],生成元与一般函数复合构造[12],2007 年,提出了一种利用连续可导的实值函数构造生成元的方法[13],同时,基于已有的对阿基米德Copula 生成元的研究,讨论了一类半参数阿基米德Copula 生成元的构造[14],对阿基米德Copula 函数的研究愈发完善[15].该文基于变换的思想,提出了基于拉普拉斯变换和z 变换的两类构造阿基米德Copula 生成元的新方法.
2 阿基米德Copula 函数定义
定义[1]设φ 是[0,1]→[0,∞]的连续的、严格单减的凸函数,满足φ(1) =0,φ[-1]:[0,∞]→[0,1]是函数φ的广义逆函数,其定义为
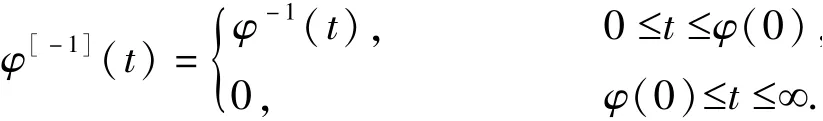
则具有C(u,v) =φ[-1](φ(u) +φ(v))形式的C 称为阿基米德Copula,其中函数φ 称为阿基米德Copula 函数C 的生成元.
如果φ(0) =∞,此时,φ[-1]=φ-1,C(u,v) =φ-1(φ(u) +φ(v))称为严格的阿基米德Copula.
3 阿基米德Copula 生成元的性质
近年来,阿基米德Copula 被广泛应用于相关性和相关结构的研究[2-6],应用于金融领域的各个领域[7-10].金融资产间的相关结构比较复杂,给出多种阿基米德Copula,选择何种Copula 模型描述相关结构是金融相关性建模的关键.由于阿基米德Copula 的性质完全取决于其生成元,因此对生成元的探究尤为重要,本文的目的是研究阿基米德Copula 生成元的构造,基于生成元已有的一些性质,本文将讨论生成元的另外两个性质,并给出具体证明,为后文研究生成元的构造做铺垫,同时进一步地扩大了生成元的范围.
性质3.1 阿基米德Copula 生成元的正的伸缩变换仍是生成元.即
设φ(s)是阿基米德Copula 的生成元,则λφ(s)也是阿基米德Copula 的生成元,其中λ 为参数且λ >0.
证明: 设h(s) =λφ(s),因为φ(s)是阿基米德Copula 生成元,所以φ(s)满足生成元的所有条件,则
①h(1) =λφ(1) =0;
②显然h(s)是连续的;
③由h'(s) =λφ'(s) <0,所以h(s)是严格单减的;
④由φ(s)是凸函数,对任意实数μ∈(0,1),s1,s2∈[0,1],有
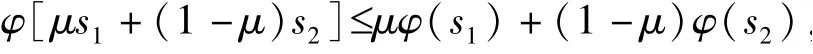
所以

即h(s)为凸函数.又由φ(s):[0,1]→[0,∞],得h(s):[0,1]→[0,∞],所以λφ(s)也是阿基米德Copula 的生成元,其中λ 为参数且λ >0.
性质3.2 阿基米德Copula 生成元的正的线性组合仍是生成元.即
设φi(s)是阿基米德Copula 的生成元,i =1,2,…,n,则也是阿基米德Copula 的生成元,其中λi为参数且λi>0.
②显然φi(s)是连续的;
④由φi(s)是凸函数,对任意实数μ∈(0,1),s1,s2∈[0,1],有φi[μs1+(1 -μ)s2]≤μφi(s1) +(1 -μ)φi(s2),所以
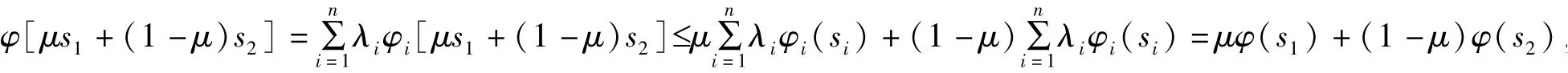
即φ(s)为凸函数.又由φi(s):[0,1]→[0,∞],得φ(s):[0,1]→[0,∞],所以也是阿基米德Copula 的生成元,其中λi为参数且λi>0.
4 构造阿基米德Copula 生成元
目前构造阿基米德Copula 生成元主要是从变换和函数两个角度考虑,同样地,本文从变换的角度出发,分别基于拉普拉斯变换和z 变换来构造生成元.下面首先讨论基于拉普拉斯变换来构造阿基米德Copula 生成元.
4.1 基于拉普拉斯变换构造阿基米德Copula 生成元
考虑到拉普拉斯变换有单边和双边之分,我们分别从单边Laplace 变换和双边Laplace 变换讨论对阿基米德Copula 生成元的构造.下面将讨论基于单边拉普拉斯变换构造阿基米德Copula 生成元.
4.1.1 基于单边拉普拉斯变换构造阿基米德Copula 生成元
在给出该构造方法之前,先提出已有的构造阿基米德Copula 生成元的方法——Laplace 变换法[11].
引理4.1[11]设F(θ)是非负随机变量θ 的分布函数且为连续函数,f(θ)是对应的概率密度函数,φ(s) =则φ-1(s)是一个严格的阿基米德Copula 的生成元,其中φ(s)表示对f(θ)的单边拉普拉斯变换.
从引理4.1 可以看出,Laplace 变换法构造阿基米德Copula 生成元中,f(θ)必须是一种特殊的函数——密度函数,当f(θ)不再只是密度函数,而是定义在R+上的一个非负连续函数时,本文有如下结论:
定理4.1 设f(θ)是定义在R+上的非负函数(即f(θ)≥0, θ∈R+)则φ-1(s)是一个严格的阿基米德Copula 的生成元,其中表示对f(θ)的单边拉普拉斯变换.
证明: 若验证φ-1(s)为阿基米德Copula 生成元,首先需验证φ-1(s)满足生成元的几个条件,即φ-1(1) =0,且是连续、严格递减、凸函数.记有
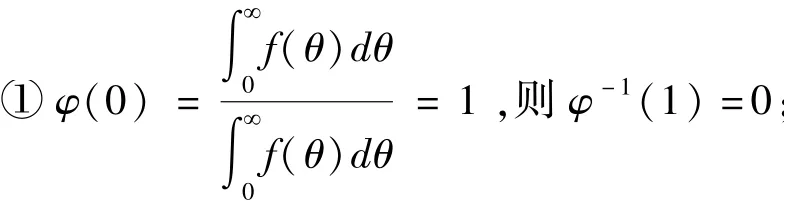
②由φ(s)的表达式易知φ(s)连续,则φ-1(s)显然也是连续函数;

由(3)知φ'(s) <0,所以φ''(s)≥0 当且仅当[φ-1(y)]''≥0,即φ 为凸函数当且仅当φ-1为凸函数.故只需证φ(s)为凸函数.

则
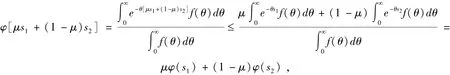
即φ 为凸函数,则φ-1也为凸函数.又φ(∞) =0,则φ-1(0) =∞,则φ-1(s)是一个严格的阿基米德Copula 的生成元.
在除法模式下,给出阿基米德Copula 的生成元的一种构造方法.不难发现,Laplace 变换法[11]是定理4.1 的特殊形式,当定理4.1 中的f(θ)是某个非负随机变量θ 的密度函数时,即可得到引理4.1,从特殊推广到一般,f(θ)的取值范围不再局限于密度函数.事实上,凡是满足R+上的非负连续函数,都可由定理4.1 构造阿基米德Copula 生成元,进一步扩大了f(θ)的范围,从而扩大了生成元的范围.
例4.1.1.1 设f(θ) =λe-θ, θ≥0,其中λ 为参数且λ >0,其拉普拉斯变换为
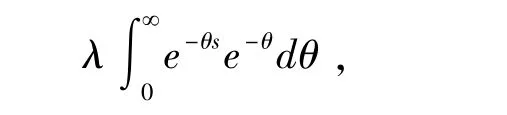
于是
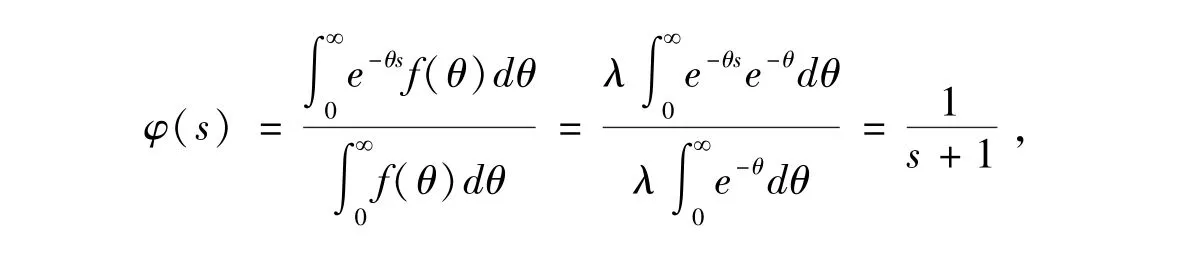
则
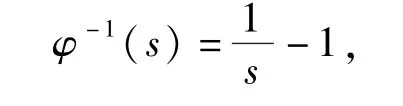
即为一个阿基米德Copula 生成元.
此时,由生成元φ-1(s)生成的阿基米德Copula 为文献[1]把该Copula 记为,在列出的常见22 族阿基米德Copula 中,该Copula 是其中某一族Cθ[11]的一员1],其中当θ =1 时
基于单边拉普拉斯变换,下面给出阿基米德Copula 生成元的另一构造方法.
定理4.2 设f(θ)是定义在R+上的非负函数(即f(θ) ≥0,θ ∈R+)s ∈[0,1],则φ(s)是一个阿基米德Copula 生成元,其中∫∞0 e-θsf(θ)dθ 表示对f(θ)的单边拉普拉斯变换.
证明: 若验证φ(s)为阿基米德Copula 生成元,首先需验证φ(s)满足生成元的几个条件,即φ(1) =0,且是连续、严格递减、凸函数.记有
②由φ(s)的表达式可知φ(s)是连续的;
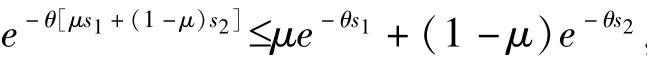
则

在减法模式下,给出阿基米德Copula 生成元的另一构造方法.生成元的形式范围不再局限于除法模式下的单边拉普拉斯变换,丰富了阿基米德Copula 生成元的构造方法,有利于我们在实际生活中选取最为恰当的生成元.

于是
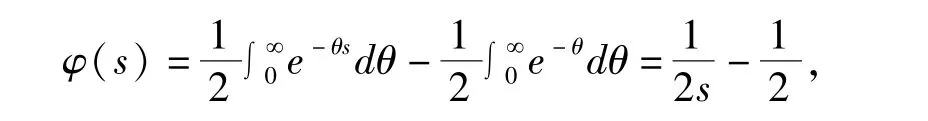
为一个阿基米德Copula 的生成元.
此时,φ-1(s) =,由生成元φ(s)生成的阿基米德Copula 为C(u,v) =,此Copula 为常见的22族阿基米德Copula 函数中的某一族的一员[11].
4.1.2 基于双边拉普拉斯变换构造阿基米德Copula 生成元
基于单边拉普拉斯变换已经提出两种阿基米德Copula 生成元的构造方法,同样地,结合单边拉普拉斯变换的思想,基于双边拉普拉斯变换,运用相关理论知识,下面提出阿基米德Copula 生成元的另外两种构造方法.
定理4.3 设f(θ)是定义在R 上的非负函数且为偶函数[0,∞],则φ-1(s)是一个严格的阿基米德Copula 的生成元,其中∫∞-∞e-θsf(θ)dθ 表示对f(θ)的双边拉普拉斯变换.
例4.1.2.1 若随机变量θ 服从区间( -1,1)的均匀分布,即分布函数为

概率密度函数为
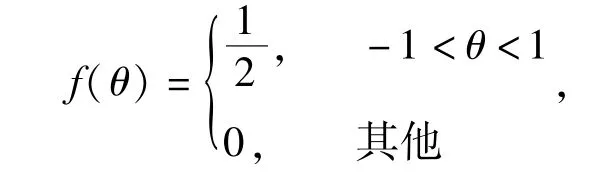
则
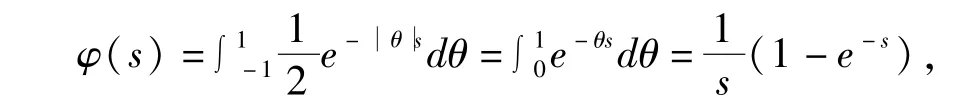
(注: 函数W(x)称为Lambert 函数,它是超越方程y =xex的解)
定理4.4 设f(θ)是定义在R 上的非负函数且为偶函数,则φ(s)是一个阿基米德Copula 生成元,其中表示对f(θ)的双边拉普拉斯变换.
本节讨论了定义在整个实数空间R 上的一类特殊函数,针对此类函数提出了两种基于双边拉普拉斯变换来构造生成元的方法,扩大了阿基米德Copula 生成元的范围,有利于实际中对阿基米德Copula 生成元的应用讨论.
4.2 基于z 变换构造阿基米德Copula 生成元
目前构造阿基米德Copula 生成元的方法主要基于变换[11]和函数构造[12-14],从变换的角度考虑,本文提出了一种新的基于z 变换的构造阿基米德Copula 生成元的方法.
定理4.5 设f(θ)是定义在N 上的非负函数(即f(θ)≥0, θ∈N),则φ(z)是一个阿基米德Copula 生成元,其中表示对f(θ)的z 变换.
证明: 若要验证φ(z)为阿基米德Copula 生成元,需验证φ(z)满足生成元的几个条件,即φ(1) =0,且是连续、严格递减、凸函数.记有
则
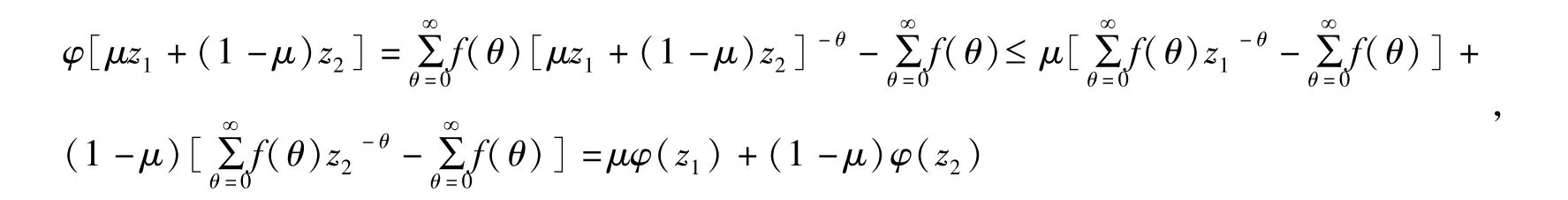
该方法从形式上看十分简便,构造生成元不再只局限于拉普拉斯变换,本文采用了一种全新的z 变换,立意新颖,丰富了构造阿基米德Copula 生成元的方法.
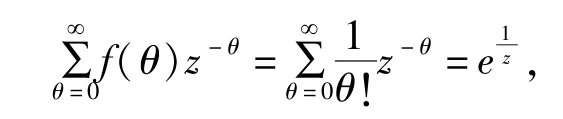
于是
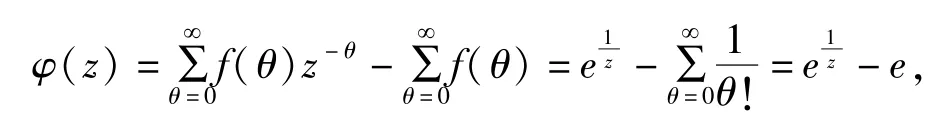
为一个阿基米德Copula 生成元.
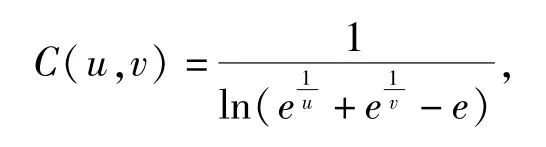
在常见的22 族阿基米德Copula 中,该Copula 是其中某一族Cθ[15]的一员(0,∞),其中当θ =1 时,
例4.2.2 若随机变量θ 服从参数为λ(λ >0)的泊松分布,即分布函数为,概率分布列为
其z 变换为


于是
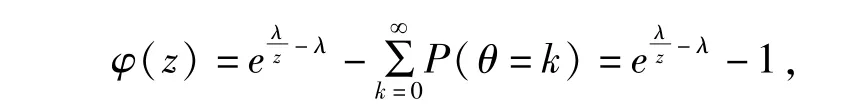
即为一个阿基米德Copula 生成元.
该Copula 是常见的22 族阿基米德Copula[15]中的某一族.
5 小结
阿基米德Copula 在统计决策、数值模拟中有广泛的应用.本文提出了基于拉普拉斯变换和基于z 变换的两类构造阿基米德Copula 生成元的新方法,证明了这两类新的构造方法确实满足生成元的相关性质,并给出了具体的例子,避免了从严格单减的凸函数中构造阿基米德Copula 函数的生成元,丰富了构造阿基米德Copula 函数生成元的方法,有利于实际生活中对阿基米德Copula 函数的研究.

