构造多维阿基米德Copula生成元的方法

(兰州交通大学数理学院 甘肃 兰州 730000)

一、引言

阿基米德Copula作为Copula函数类的一种特殊Copula，阿基米德Copula由于构造方便、计算简单，且有很多良好的性质在许多领域尤其是金融领域得到了广泛应用.目前对于阿基米德Copula的研究已经有了很多成果，阿基米德Copula是由生成元构成的copula，生成元是一种单调递减的凸函数.有了生成元就可以构造出阿基米德Copula.文献[3]中提出了构造阿基米德Copula生成元的常见方法：拉普拉斯变换法.之后在文献[6]中提出了利用可导的条件构造生成元的方法，在文献[7]中对于阿基米德Copula的生成方法也从加法推广到乘法，文献[4]则将构造方法不再局限于概率密度函数而是拓展到实数范围.李霞将这些对于阿基米德Copula的研究成果都编绘进文献[5]中，基于以上研究，本文由单一参数推广到多参数构造生成元的方法进行了研究，提出了多维阿基米德Copula生成元的构造方法.

二、预备知识

(一)阿基米德Copula函数定义

定义1[2]：设φ是[0,1]→[0,∞]上的连续的、严格降的凸函数，且φ(1)=0，则φ的伪逆φ[-1]是[0,∞]→[0,1]上的函数，且

则具有C(u,v)=φ[-1](φ(u)+φ(v))形式的Copula称为阿基米德Copula，φ称为Copula函数的生成元.如果φ(0)=∞，则称φ为严格的生成元.此时，φ[-1]=φ-1，C(u,v)=φ-1(φ(u)+φ(v))称为严格的阿基米德Copula函数.

(二)阿基米德Copula生成元的常用构造方法

三、二维阿基米德Copula生成元的构造方法

目前对于构造阿基米德Copula生成元主要从变换和函数角度进行研究，本文将从维数角度去考虑构造生成元，首先讨论在二维的条件下构造阿基米德Copula生成元.

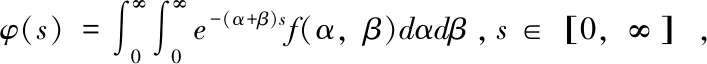
证明：若要验证φ-1(s)为阿基米德Copula生成元，需要φ-1(s)满足阿基米德Copula生成元的几个条件，其中需要φ-1(1)=0，φ-1(s)是连续的、严格递减、凸函数.

(2)φ(s)由表达式显然连续，则φ-1(s)也连续；

(4)已知φ-1为凸函数当且仅当φ为凸函数，所以只需证明φ为凸函数.

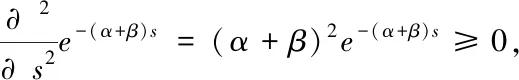
由上可知φ(s)是凸函数，则φ-1(s)为凸函数，又因为φ(∞)=0，则φ-1(0)=∞，即可证明φ-1(s)是一个严格的阿基米德Copula的生成元.

例1：设二维独立随机变量(α,β)具有密度函数f(α,β)=e-(α+β)，其中α,β≥0，则对密度函数进行拉普拉斯变换

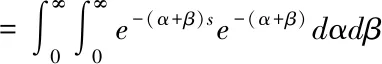
以上被积函数中的f(α,β)是密度函数，比较特殊，当f(α,β)不再是密度函数而是定义在R+×R+上非负连续函数时，以下定理能被得出.

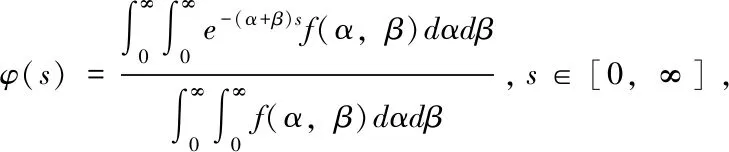
证明：此定理的证明和定理1的证明步骤相同，则着重证明φ-1为凸函数.

由上已知φ-1为凸函数当且仅当φ为凸函数，所以只需证明φ为凸函数.

所以φ(s)是凸函数，则φ-1(s)为凸函数，又因为φ(∞)=0，则φ-1(0)=∞，即可证明φ-1(s)是一个严格的阿基米德Copula的生成元.

四、多维阿基米德Copula生成元的构造方法

通过讨论二维阿基米德Copula生成元的构造方法，我们可以推广到多维上来构造生成元，这样扩大了阿基米德Copula生成元的生成条件，有利于阿基米德Copula函数的应用在实际中.下面给出了多维非负连续函数构造生成元的方法.

证明：

(2)φ(s)由表达式显然连续，则φ-1(s)也连续；

(3)φ′(s)=

e-(θ1+θ2+…+θn)[λs1+(1-λ)s2]≤λe-(θ1+θ2+…+θn)s1+(1-λ)e-(θ1+θ2+…+θn)s2

则

所以φ(s)是凸函数，则φ-1(s)为凸函数，又因为φ(∞)=0，则φ-1(0)=∞，即可证明φ-1(s)是一个严格的阿基米德Copula的生成元.

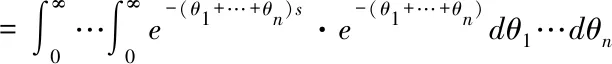
这样可以和例1结合得到如下多维阿基米德Copula函数

五、小结

阿基米德Copula函数在模型选择，建立数据之间的简单联系有着重要的作用.本文基于前人研究基础上扩大了求取生成元的条件，不再局限于严格单减的凸函数和一维函数，但是还有待研究对于随机变量是不独立的情况下构造生成元这一难题.