码长为2nps的重根自对偶负循环码
常星星, 孔 琼, 郭膑化
(山东理工大学 理学院, 山东 淄博 255091)
负循环码是一类重要的线性码.它们具有很好的代数结构、循环性,其编码和译码可以利用线性移位寄存器来实现.寻找有限域上自对偶负循环码是学者们研究的热点之一.文献[1]中研究了下列码类:(1)有限域Fq上码长为2n的单根常循环码;(2)Fq上码长为2n的单根自对偶负循环码;(3)Fq上码长为2nps的重根常循环码.目前Fq上码长为2nps的重根自对偶负循环码尚未给出.本文将给出Fq上码长为2nps的重根自对偶负循环码.
1 预备知识
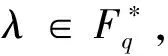
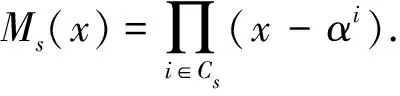
引理1(文献[1]中引理4和引理5)设n≥1,d≥2,c是奇数.
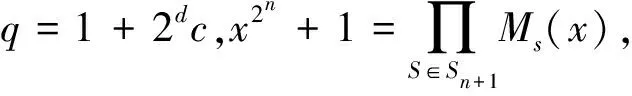
当n≤d-1时,Sn+1={±1,±3,…,±3(2n-1-1)}.

2 主要结果
下面给出Fq上码长为2nps的所有重根自对偶负循环码.
定理1设n≥1,s≥1,q=1+2dc,d≥2,c为奇数.
1)如果n≥d,那么Fq上码长为2nps的自对偶负循环码有(ps+1)2d-2个:
2)如果n≤d-1,那么Fq上码长为2nps的自对偶负循环码有(ps+1)2n-1个:



又因为当s取遍集合Sn+1,-s也取遍集合Sn+1,所以,
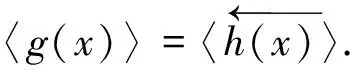
2)类似可以证明当n≤d-1的情况成立.
定理2设n≥1,s≥1,q=-1+2dc,d≥2,k=1,c为奇数.
1)如果d=2,那么Fq上码长为2nps的自对偶负循环码有(ps+1)2d-2个:
2)如果n≥d≥3,那么Fq上码长为2nps的自对偶负循环码有(ps+1)2d-2个:
3) 如果n≤d-1,d≥3,那么不存在Fq上码长为2nps自对偶负循环码.
证明1)和 2)同定理1中的证明类似.
3)如果n≤d-1,d≥3,设C=〈g(x)〉为Fq上码长为2nps的自对偶负循环码,由引理1得
其中0≤j3i≤ps,那么
当q=5时,M1(x)=x2n-1-2,M-1(x)=x2n-1+2;当q=3时,M1(x)=x2n-1-x2n-2-1,M-1(x)=x2n-1+x2n-2-1.根据定理1和定理2得到下面推论.
推论11)设q=5,对任何n≥1,s≥1,F5上码长为2n5s的自对偶负循环码有5s+1个:〈(x2n-1-2)v0(x2n-1+2)5s-v0〉,0≤v0≤5s.
2)设q=3,对任何n≥2,s≥1,F3上码长为2n3s的自对偶负循环码有3s+1个:
〈(x2n-1-x2n-2-1)v0(x2n-1+x2n-2-1)3s-v0〉,0≤v0≤3s.
例 当n=1,s=1,那么F5上码长为10的自对偶负循环码有6个,详情见表1.
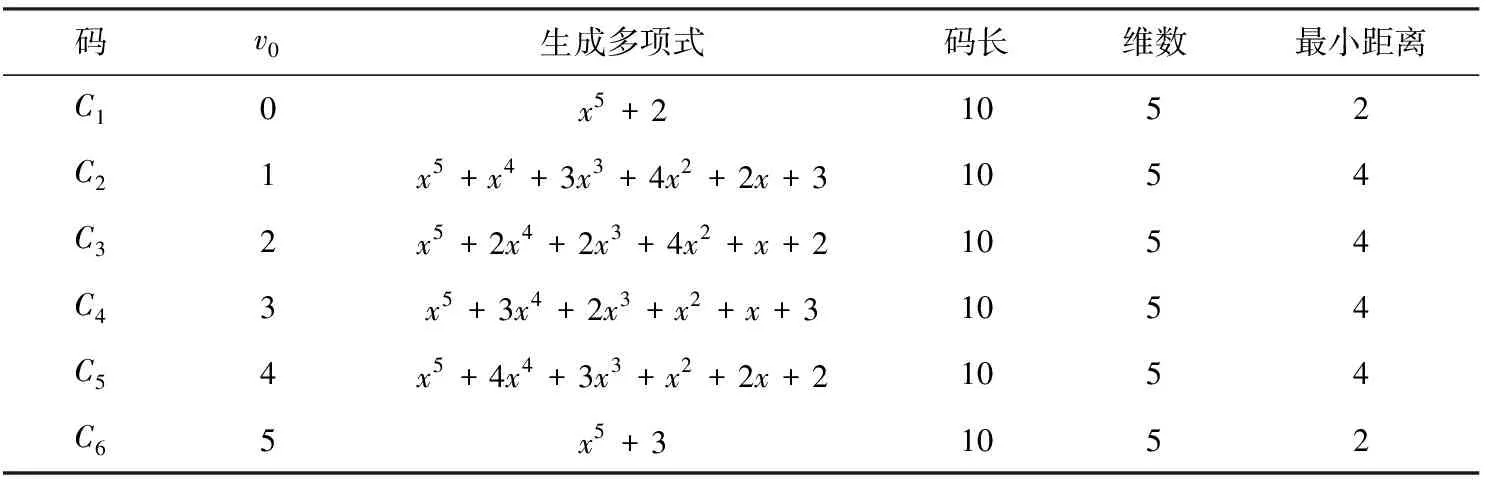
表1 F5上码长为10的自对偶负循环码
[1]Gurmeet K.Bakshi, Madhu Raka.A class of constacyclic codes over a finite field[J].Finite Fields Appl.2012,18: 362-377.
[2]王开洪.关于常循环码[J].渝西学院学报,2003,1(2):10-12.
[3]冯克勤.纠错码的代数理论[M].北京:清华大学出版社,2005:56-57.
[4]陈鲁生,沈世镒.编码理论基础[M].北京:高等教育出版社,2005:157-158.

