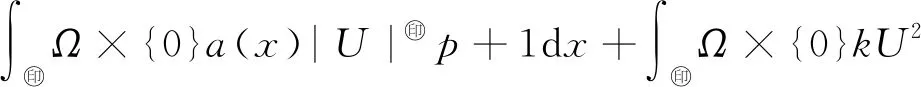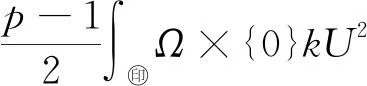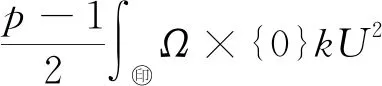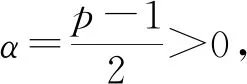一类半线性分数阶反应扩散方程解的性质
彭红玲, 樊明书
(西南交通大学 数学学院, 四川 成都 610031)
1 简介
主要研究如下一类半线性分数阶反应扩散方程

(1)

分数阶Laplacian算子的定义有多种,常用的有如下3种定义.

定义 1.2[2-4]假设g:RN→R的速降函数,(-Δ)sg的定义如下:
(-Δ)sg(x)=CN,sP.V.
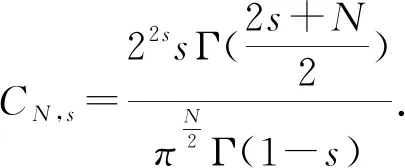
从定义1.2可以看出,(-Δ)s是以积分形式定义的一个非局部算子,Caffarelli等在文献[5]中用延拓的方法将非局部的Laplacian算子化为局部可变分的算子,并给出等价定义.
定义 1.3[5]u:RN→R速降函数,U:RN×[0,∞)→R是u的延拓,函数U满足



用定义1.3来定义分数阶Laplacian算子.
Cortazar等[6]发表半线性抛物方程
的爆破问题,其中Ω是RN中的光滑有界凸区域,M≥0,V是Lipschitz连续的,φ(x)>0且满足相容性条件.
Winkler等[7]研究了抛物方程
其中v是∂Ω的外法向量.文章指出λ>0时有整体解,也存在爆破正解.
Vázquez等[8]发表对分数阶多孔介质方程(FPME)
在RN空间中Cauchy问题解的存在性和唯一性,其中0<σ<2,m>0.
Tan等[9]研究了如下半线性分数阶反应扩散方程


近年研究分数次p-Laplacian算子问题的还有文献[10-12]等.
下面对方程(1)用Caffarelli-Silvestre的延拓法.令U:Ω×(0,∞)→R是函数u:Ω→R的延拓函数,记D={(x,y)|(x,y)∈Ω×(0,∞)},D的横向边界为∂LD=∂Ω×[0,∞),可将(1)式化为

(2)
记(-Δ)s=As,(-Δ)s/2=As/2,0 u∈Hs0(Ω). (4) 受文献[9,13-16]的启发,定义 H(U)=h(U)-f(U)-g(U). 对E(U(t))关于t求导,可得 ∇U·∇Utdxdy- (5) 所以E(U(t))关于t单调递减,且有 即 势阱的深度:d=infU≠0}. 本文的主要结果如下. 定理 1.3若U=U(x,y,t;U0)是(2)式的解,且存在t0≥0使得E(U(t0))≤0,则当k<0时,U在有限时间内爆破. 为证明解的整体存在性,先引入4个引理. H(U)=h(U)-f(U)-g(U)>0}. 令 故 即 (λ-λp)(h(U)-f(U))≥0, 则 而p>1,故 E(λU)> 引理2.2的证明可参见文献[17-19],此处省去证明. 证明因为 所以 若设 由于a(x)∈[m,M],则 故 ρn(x)=min{|x|2s,n}, γn(u)=min{ku,n}, βn(u)=min{a(x)|u|p-1u,n}, (7) 引理2.4的证明过程用到了Gal⊇rkin方法,此处省去证明,引理2.4和2.5的证明过程具体可参照文献[9].接下来给出定理1.1的证明. I(u0)+ε0 (8) 第一种情况与(8)式矛盾,将第二种情况代入I(un)有 I(udx- (9) (10) 由(10)式可得 (12) 对(12)式的左边,由分数阶Sobolev不等式,当p=2时,有 (13) 其中c>0.结合(11)~(13)式可得 所以方程(2)的解整体存在. 下面给出定理1.2的证明. 定理1.2证明对任意序列tn→∞,令Un=U(x,y,tn;U0).由于自反巴拿赫空间的有界列都是弱紧的,结合引理2.5,存在序列{Un}和函数U使得: U UnUinLp+1(Ω×{0}), U 令测试函数 φ(x,y,t)= 其中 ψ∈Hs 由弱解的定义,有 将φ代入上面的式子,可得 对第二项,用分部积分法,结合ρ(0)=ρ(1)=0,有 则 a(x)|U|p-1Uρ(t-tn)ψ+ kUρ(t-tn)ψ)dx]dt=0. 令δ=t-tn,则 a(x)|U(tn+δ)|p-1U(tn+δ)ρ(δ)ψ+ kU(tn+δ)ρ(δ)ψ)dx]dδ=0. (14) ‖U(tn+δ)-ωδ‖Lp+1(Ω×{0})→0, ‖U(tn)-ω‖Lp+1(Ω×{0})→0. 下证在Ω×{0}中几乎处处有ωδ=ω.结合能量等式和Hölder不等式,有 因为0≤δ≤1,当tn→∞时‖U(tn+δ)-U(tn)‖L2(Ω×{0})→0,即在Ω×{0}中几乎处处有ωδ=ω.重新整理(14)式可得 a(x)|U|p-1U(tn)ρ(δ)ψ+ kUρ(δ)ψ)dx]dδ- ∇U(tn))ρ(δ)·∇ψdxdydδ+ U(tn))kρ(δ)ψdxdδ=0. 由勒贝格控制收敛定理,当tn→∞时,上式等号左端后四项趋近于0,对等号左端第二项有 即U(tn)在弱意义上趋近于(2)式的稳态解. 给出定理1.3的证明. 定理1.3证明(反证法) 若t=∞,令 对t求导,可得 在(2)式的两边同乘以U,再在D上积分,有 (15) 在能量等式(6)两边同乘p+1 ,再加上(15)式有 (p+1)E(U(t0)), 因为E(U(t0))≤0,k<0,所以对∀t≥t0,有 所以 (16) 由Hölder不等式,有 r′(t1)(t-t1)→∞, 由此,当t>t1,可得 两边同时积分,可得 r′(t0))2lnr(t)|tt1→∞, r(t)r″(t)>(1+α)(r′(t))2. 0 J(t3)+J′(t3)(t-t3)→-∞,t→∞, 显然矛盾,故U在有限时间内爆破.

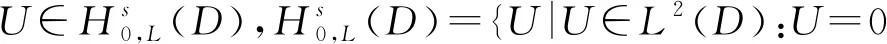



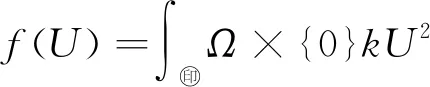
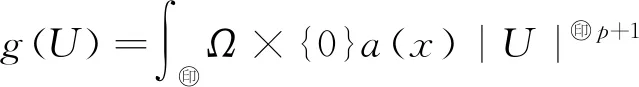

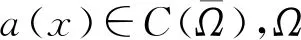


2 整体解和渐进行为



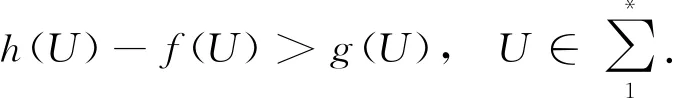

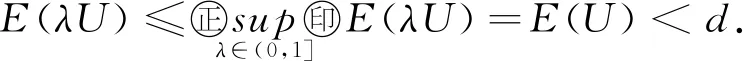



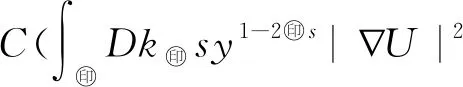


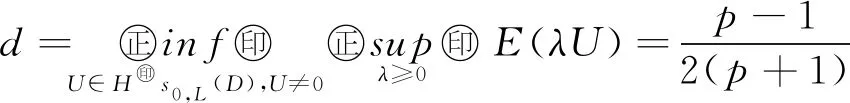




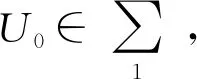
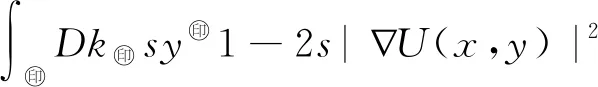

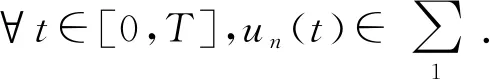













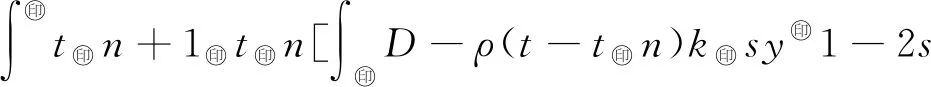


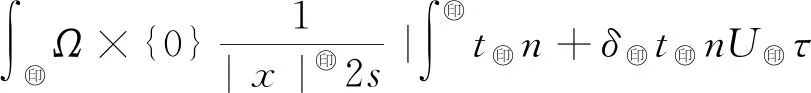




3 爆破