一类次线性Hill型方程的无穷小周期解
王梓欢, 王 超
(盐城师范学院 数学与统计学院, 江苏 盐城 224002)
本文考虑二阶Hill型微分方程
x″+q(t)g(x)=0,
(1)

(g0)g(x)·x>0,
(g1)
非线性Hill型方程是一类重要的时变位势方程,它因具有实际的应用背景而广受关注.针对方程
x″+a(t)|x|γ-1x=0,γ>0,
(2)
在a(t)允许变号的前提下,Waltman[1]首先研究了方程
x″+a(t)x2n+1=0,n∈N
解的振动性.针对方程(1)的周期解问题,当g(x)在无穷远处满足超线性条件
(3)
时(例如,在方程(2)中γ>1),Butler[2]证明了无穷多个大范数的周期解的存在性;在原点处满足超线性条件
(4)
时(例如,在方程(2)中γ<1),Butler[3]证明了在原点附近存在无穷多个周期解.
在超线性条件(3)下,Papini[4]运用Butler的证明方法证明了方程(1)的Floquet-type边值问题无穷多个解的存在性,这个结果也包含了Butler的结果.同时,Papini运用这个边值问题的结果也证明了方程
x″+cx′+q(t)g(x)=0
有无穷多个周期解的存在性.在条件(g0)、g∈C1(0,+∞)、g(0)=0以及在原点处满足超线性条件
的情况下,关于小范数周期解的存在性,Bandle等[5]推广了Butler的结果.另外,在一些超线性条件下,有关方程(1)周期解和其他动力行为研究的一些结果可见文献[6-11].
最近,针对权函数q(t)为正函数的情形,文献[12]在一类关于时间映射的超线性条件下,证明了带强迫项的对称非线性Hill型方程
x″+q(t)g(x)=p(t)
有无穷多个对称调和解,同时,证明了对称次调和解具有稠密性分布.当周期解的最小正周期T0等于系统的最小正周期T时称为调和解,当T0=mT(m>1为正整数)时称为次调和解,相关的定义可见文献[13]的定义1.文献[14]在g(x)是有界函数的条件下,证明了方程(1)无穷多个次调和解的存在性,且当q(t)是偶函数时,证明了无穷多个偶次调和解的存在性和偶次调和解的稠密性分布结果.
在上述结果中,绝大多数都是大振幅的周期解.文献[3]和[5]的小振幅的周期解的存在性结果是在原点附近满足超线性条件下得到的,而且在文献[5]中要求g∈C1(0,+∞).一个有趣的问题是,当g(x)仅仅是连续函数且在原点附近满足次线性条件(g1)时,方程(1)是否有无穷多个周期解?
本文在第1节首先运用相平面分析的方法对等价系统解的动力行为进行分析,得到了在充分小的圆盘内系统解的动力行为.第2节在充分小的区域内构造了一系列的圆盘使得系统的Poincaré映射在圆盘的边界具有扭转性,从而运用推广的Poincaré-Birkhoff扭转定理[15]证明无穷多个小振幅的次调和解的存在性.
本文的主要结论是:
定理 A假设(g0)、(g1)成立,则方程(1)至少存在一个调和解和无穷多个次调和解.
1 引理
令x′=y,则y′=-q(t)g(x),方程(1)等价于
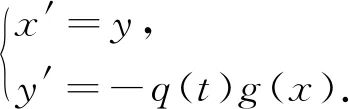
(5)
设连续截断函数η:R2→R为
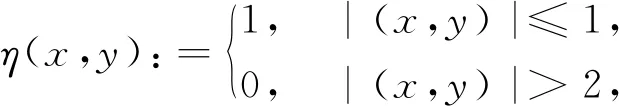
且满足0≤η(x,y)≤1.


(6)
的解(x(t),y(t))满足
|(x(t),y(t)|≤1, ∀t∈I,
则(x(t),y(t))就是(5)定义在区间I上的解.
下面首先研究方程(6)的周期解的存在性和重性问题.
由g(0)=0知原点为系统(6)的平衡点,由解的唯一性可知从原点外任一点出发的解都不会经过原点.在半径为2的圆域之外系统(6)为
x′=y,y′=0,
易见系统(6)的解在有限时间内不会跑到无穷远处.
下面总假设(x(t;x0,y0),y(t;x0,y0))为方程(6)满足初值(x(0),y(0))=(x0,y0)的解.
引理 1.1∀(x0,y0)∈R2,解(x(t;x0,v0),y(t;y0,v0))在(-∞,+∞)上有定义.
引进极坐标.假设(x0,y0)∈R2,则解(x(t;x0,y0),y(t;x0,y0))可以用极坐标表示

(7)
其中r(t),θ(t)是连续函数.易证,在坐标变换(7)下,(r(t;r0,θ0),θ(t;r0,θ0))满足方程
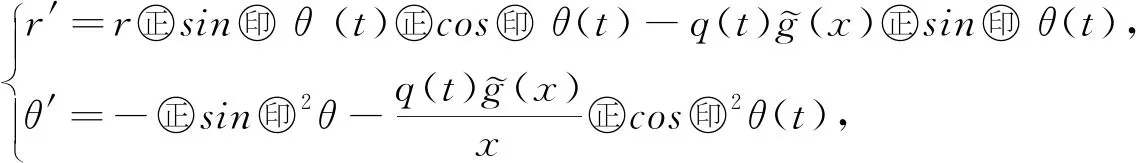
其中x0=r0cosθ0,y0=r0sinθ0.
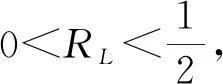
1) 若r1≤r0≤RL,则
r(t;r0,θ0)≥r2, ∀|t|≤L;
2) 若0 则由(8)式知 其中q0=从而 r0ee 从而,有 r0ee 取RL>0使得RL则 对∀0 引理 1.3对方程(8)的任意解(r(t),θ(t)),若0 引理 1.4设(g0)和(g1)成立.若(r(t),θ(t))是方程(8)的解且满足 0 和 θ(t2)-θ(t1)=-2π, 则 由条件(g1),对上述的ε,存在δ>0使得当0 从而 得证. 引理 1.4指出,在条件(g1)下,方程(8)的解的范数越小,则解在相平面上经过区域I:={(x,y):-ε≤θ≤0}就越慢,从而绕原点转一圈所需要的时间就越长.下面,类似于文献[16-17]中的证明方法,可以证明下面的引理. L(R)≤r(t)≤R, ∀t∈[t1,t2], 则 θ(t2)-θ(t1)<-π. 证明只证明r(t1)=R,r(t2)=L(R)的情况,r(t1)=L(R),r(t2)=R的情况可以类似证明. 由(g0),对任意的x≠0有g(x)·sgn(x)>0.定义连续函数g1:[-1,1]→R如下: 由构造知,g1是单调非减函数.易见,当0 g2(x) 对所有的x∈(0,1]有 g2(x) 其中,q0:=类似地,定义一个[-1,1]上的连续的单调非减函数h(x),使得h(0)=0且对所有的x∈[-1,0)有 h(x)>q1g1(x), 对所有的x∈(0,1]有 h(x)>q0g1(x). 定义上凹函数 显然, 0 G(x)>H(x)>0,x<0. 易见, 对任意的r∈(0,1],记 B(r):={(x,y):x2+y2 且取k>0使得对任意的 有 取-R 易见,曲线Γ1与Γ2均在圆B(R)内. 因为H是上凹的,对每一个y∈R,最多有两个数x1,x2使得(x1,y)∈Γ1,(x2,y)∈Γ1.对Γ2也有相同的结论.显然,存在0 这意味着在Γ1上的每一点处,方程(6)的向量场都是从内指向外的.对Γ2也有相同的结论.同时,易证,在线段{(x,0):γ≤x≤1}上,向量场指向下方. 因此,若(x(t),y(t)):[t1,t2]→R2是方程(6)的以 (x(t1),y(t1))∈{(x,y):y≤0,|(x,y)|=R} 为初始条件的解,满足|(x(t2),y(t2))|=L(R)以及|(x(t),y(t))|≤R,∀t∈[t1,t2],则一定存在t1<ω (i)β≤x(ω)≤γ,y(ω)=0; (ii) ∀t∈[t1,ω),(x(t),y(t))与Γ1与Γ2均不相交; (iii)u′(t)在[t1,ω]内至少有两个零点. 这意味着曲线t(x(t),y(t))在穿过线段{(x,0):β≤x≤γ}之前绕原点至少旋转了π,即θ(ω)-θ(t1)≤-π.由引理1.3知θ(t2)-θ(t1)<-π. 对于满足 (x(t1),y(t1))∈{(x,y):y≥0,|(x,y)|=R} 的解也有类似的构造及相应的讨论.因此,可以选择一个适当小的正数L(R) R≤r(t)≤L(R,j), ∀t∈[t1,t2], 则 θ(t2)-θ(t1)<-2jπ. 证明由引理1.5,令R1:=L(R) θ(t2)-θ(t1)=(θ(t2)-θ(s2))+ (θ(s2)-θ(s1))+(θ(s1)-θ(t1))< -π-π=-2π. 令L(R,1):=R2,则结论对j=1成立. 令R3:=L(R2)及R4:=L(R3),类似可证,如果(r(t),θ(t))是方程(8)的满足r(t1)=R,r(t2)=R4(或者r(t1)=R4,r(t1)=R)及 R4≤r(t)≤R, ∀t∈[t1,t2] 的解,则 θ(t2)-θ(t1)<-2·2π=-4π. 令L(R,2):=R4,则结论对j=2成立.反复进行上述讨论,则对每一个j>0,可以找到一个正数L(R,j) R2≤r(t)≤R1, ∀t∈[t1,t2], 则 证明将圆环分成两个区域: 当(x,y)∈Ⅰ时, |x|≥R2 其中q1:=当(x,y)∈Ⅱ时, θ′<- 因此,存在b>0使得θ′≤-b.从而θ(t2)-θ(t1)≤-b(t2-t1).得证. 证明下面,先证明方程(1)存在无穷多个次调和解. θ(mT)-θ(0)<-2jπ. 设(r(t),θ(t))是方程(8)的解,r(0)=R2,满足: 情况1或者(x(t),y(t))∈A,∀t∈[0,mT],其中(x(t),y(t))由(7)给出; 对前一种情况,已知θ(mT)-θ(0)<-2jπ. 对后一种情况,可以选择一个区间[t1,t2]⊂[0,mT]使得: 情况3或者r(t1)=R2,r(t2)=R1且对∀t∈[t1,t2]有R2≤r(t)≤R1; 情况4或者r(t1)=R2,r(t2)=R3且对∀t∈[t1,t2]有R3≤r(t)≤R2. 由R1、R2和R3的选取,无论哪种情况都有θ(t2)-θ(t1)<-2jπ.由引理1.3得θ(mT)-θ(0)<-2jπ.综上所述,若(r(t),θ(t))是方程(8)的解,则 r(0)=R2⟹θ(mT)-θ(0)<-2jπ. r(t)≤S1, ∀t∈[0,mT]. 所以 r(0)=S2⟹θ(mT)-θ(0)>-2π. 考虑mT-Poincaré映射: [S2,R2]×R(r0,θ0)(r(mT;0,r0,θ0), θ(mT;0,r0,θ0)), 则由推广的Poincaré-Birkhoff扭转不动点定理知,至少存在两个点(ri,θi)∈(S2,R2)×R(i=1,2),使得方程(8)的解(r(t;ri,θi)、θ(t;ri,θi))满足 r(mT;ri,θi)=ri 并且 θ(mT;ri,θi)-θi=-2jπ,i=1,2. 它们对应系统(6)的两个mT-周期解(x(t;xi,yi),y(t;xi,yi))(i=1,2),其中 xi=ricosθi,yi=risinθi, 并且x(t;xi,yi)在[0,mT)内恰好有2j个零点. 由R2的选取可知,对∀t∈[0,mT],r(t;0,ri,θi) θ(mT)-θ(0)<-2jπ, 这与θ(mT)-θi=-2jπ矛盾.因此,(x(t;xi,yi),y(t;xi,yi))(i=1,2)是方程(5)的两个mT-周期解,即x(t;xi,yi)是方程(1)的两个mT-周期解. 显然,当j和m互素时,mT恰好就是x(t)的最小周期,从而x(t)是方程(1)的次调和解. 调和解的存在性由上述结论与Massera定理[18]即得. 注 1.1由解的弹性性质(引理1.2)知,在定理1.1的证明中,当R1→0时所得到的周期解x(t)满足






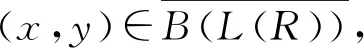


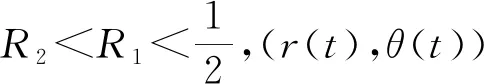

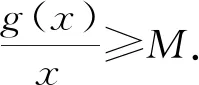
2 定理A的证明