基于参数自适应回归的电梯楼层智能识别模型
高文滨, 赵联文, 任芮彬*, 廖群英
(1. 西南交通大学 系统可信性自动验证国家地方联合工程实验室, 四川 成都 610031; 2. 四川师范大学 数学科学学院, 四川 成都 610066)
随着社会经济和城市现代化的快速发展,高层建筑在城市建筑中占比越来越大,电梯作为高层建筑必备运输工具也越来越多.当今社会出现了各种电梯的安全问题,促使电梯的第三方检测快速发展.由于不同品牌电梯的系统、硬件的不同以及电梯应用的环境不同,目前还没有通用的电梯楼层检测方法,故急需一种泛化能力强、与机械硬件不相关的电梯楼层智能识别方法.
由于大气压数据具有时效性,且采集简单,现有的电梯智能识别算法大多是基于大气压数据.首先建立气压值与海拔高度之间的函数关系,再通过海拔高度对电梯停靠楼层进行识别.文献[1]提出了基于JY901姿态角度传感器的气压测量的语音报站系统,将目标运行状态下的电梯气压差转换成海拔高度的变化,从而换算出楼层高度.文献[2]提出一种基于JY901B姿态传感器的电梯智能语音提示系统,在气压变化差值转变为海拔高度测算楼层高度的基础上,改进标准气压海拔关系式,推算出误差小且速度快的优化算法模型.上述方法具有所需装备体积小、功耗低、测量精度高的优点,但需要提前测定楼层高度以及电梯1楼的初始气压值等数据,实际使用时较为麻烦,针对外部环境的变化泛化性能较差.文献[3]提出了一种基于Wi-Fi、气压计组合的楼层定位方法,使用密度聚类区分不同区域的信号特征,在线接收信号与指纹库从而进行匹配,以此识别楼层.该方法需要Wi-Fi数据的配合,实施较为复杂,且电梯中可能存在Wi-Fi数据无法传输的情况,不利于实际电梯楼层识别工程的实施.文献[4]提出了部署纵向定位设备,再建立室内各层楼梯口的LoRa信号指纹库,划定对应不同楼层信号强度特征的判定阈值,最后结合LoRa-RSSI(received signal strength indication,接收信号强度指示)动态识别和楼层判定方法,捕捉室内动态下无线信号强度的实时变化,进行楼层识别,该方法的识别准确率是97.9%.文献[5-6]是基于指纹的室内定位方法,需要较多在设备硬件上的花费.文献[7]提出了通过传感器采集本地的气压和温度信息,利用附近基站广播信号中的基站气象信息和高程信息进行解算结合差分气压测高方法.该方法考虑到了温度这个外部因素对气压值的影响,但是没有考虑其他因素对气压值的影响,也没有直接运用到电梯楼层识别的实例.文献[8]提出了基于无线指纹和气压混合楼层识别的算法,利用无线AP(access point)分布和气压信息进行计算,通过离线训练指纹提取不同楼层的AP分布规律并采用贝叶斯分类法进行识别.该方法是从无线AP分布中获得楼层信息进行初始化和校准气压的楼层识别技术,在实验中,该方法的识别准确率超过96.1%,但尚未达到100%.文献[9]提出使用智能手机的内置气压传感器来研究移动设备的高度,并将该高度与建筑物的楼层高度进行比较从而获得楼层的数量.为了解决不同性能手机气压计带来的误判问题,还提出了邻域的压力传感器相对标定方法.该方法需测量楼层高度,在工程应用问题上相对复杂.文献[10]提出一种结合水平仪和气压计的多层建筑物室内环境中行人楼层高度识别算法,识别准确率可达93%,其需要的设备更多,且准确率未达到100%.
现有的方法为保证电梯楼层识别精度需要较高维度的数据,或需要较为复杂、昂贵的设备,不利于实际工程项目的应用.
本文将大气压数据与电梯停靠楼层之间建立直接联系.通过半监督学习的方法,初次采集带标签数据,后续数据均为无标签数据,建立参数自适应的回归模型.通过考虑机器学习中的半监督模型,更加注重目标识别的泛化能力,提出首先利用带标签训练数据拟合电梯停靠楼层与气压值的回归方程,再通过上个时间段的数据对当前时间的回归模型的参数进行调整,得到新的回归模型,从而进行精准判别.该方法数据简单易于采集,在不同情景下,可以根据实际情况,自适应地调整参数,具有较高的识别精度.而且该方法的模型复杂度不高,使用设备功耗低、数量少、成本低廉,便于在工程项目中实际运用.
1 问题分析与研究思路
在电梯楼层识别模型中,自变量为大气压值,因变量为电梯停靠楼层.经查阅文献[1-2,11-12]及对回归方程做F检验与拟合优度检验证明,在较短的时段内,大气压值与电梯停靠楼层之间,存在明显的线性关系(分析见4.2小节的显著性检验).但是随着时间的推移,普通的线性回归模型无法对电梯的停靠楼层进行准确的识别.因此,本文将基于实地采集的实验数据,建立改进的回归模型,以实现电梯所在楼层的智能识别.
但模型的建立有以下困难:
1) 实际工程应用中用于建模的带标识的数据极少,实时收集的数据为无标识数据;
2) 用于识别电梯停靠楼层的特征较少,数据维度较低;
3) 自变量大气压值与温度呈正相关,还与天气、楼梯间的通风情况等因素有一定的关系.在实际工程应用中缺少描述大气压值变化的特征,无法考虑到所有导致大气压变化的影响因素.
针对以上问题,本文提出了基于参数自适应的电梯楼层自动识别模型.该模型可以使用较少的数据,实现对电梯停靠楼层的智能识别,且算法具有较强的泛化能力.
由于线性回归模型无法对长时段的目标进行识别,本文通过模型参数的自适应调整,根据t时段数据蕴含的信息特性,对t+1时段的模型进行修正,使模型准确识别楼层的时效性在参数的持续更新下得以保证.
2 半监督学习下的目标智能识别模型
2.1 模型数据实际情况中,可能存在采集数据量较小且带标签数据不易收集的问题.该半监督学习模型只需少量初始数据带有标签信息,后续数据均不含标签.本方法将训练数据分为两个部分.第一部分为n对带标签训练数据,记为(x1,y1),(x2,y2),…,(xn,yn),用以学习模型的参数.第二部分数据需现场定时采集,每tmin时段内采集一组容量为k的无标签数据(假设tmin时段内数据的变化很小,模型可以对目标进行准确识别)用于在训练中调整模型参数,共采集T个时段(t=1,2,…,T),其中训练数据记为
Xt=(xt1,xt2,…,xtk),
t=1,2,…,T,k≪n.
2.2 模型假设针对半监督学习的参数自适应回归模型有下述3个假设:
1) 各因变量间距保持一致;
2) 自变量与因变量之间的变化关系不受外部环境影响;
3) 外部条件的改变过程缓慢,在某种意义上,短时间内认为模型可以进行准确判断,即t时刻的模型可以对[t,t+tmin]内的数据进行准确识别.
假设1)保证了自变量与因变量间的线性关系;假设2)在回归模型中自变量与因变量间的相对变化规律是固定的,即回归系数不变;假设3)保证了参数迭代的可行性.在电梯停靠楼层自动识别实际问题中,满足以上3条假设(详细情况请见第3节).
2.3 线性回归模型回归模型的输入是n组带标签数据(x1,y1),(x2,y2),…,(xn,yn).
一元线性回归模型是考虑两个变量间的相关关系[13-17],自变量x与因变量y之间的关系可解释为两个部分:y的变化一部分是由x的变化导致的,另一部分是由其他一切随机因素产生,记为ε.在实际问题中,更关注y由于x的改变产生的变化,而不是其他一切随机因素所产生的变化,即
y=β0+β1x+ε.
(1)
(1) 式称为y对x的一元线性理论回归模型.式中β0与β1是待估参数,称β0为回归常数,β1为回归系数.
在电梯停靠楼层识别问题中,对于获得的训练数据(x1,y1),(x2,y2),…,(xn,yn),xi表示停靠楼层对应的大气压值,yi表示停靠的楼层,则得到模型
yi=β0+β1xi+εi,i=1,2,…,n.
(2)

(3)
2.4 回归模型参数β0和β1的估计利用最小二乘估计对β0,β1进行估计,定义
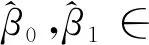
(4)
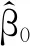
(5)
对(5)式进行求解得
(6)
2.5 参数自适应回归模型的参数β0和β1调整预测模型中,是回归系数,代表的是大气压与楼层之间的相对关系;是外部扰动,代表的是其他一切随机因素的变化,对回归方程造成的统一影响.所以需要调整预测模型的和来更精确地拟合实时数据,提升电梯楼层智能识别的精确度.
(Xt,Yt)={(xt1,yt1),(xt2,yt2),…,(xtk,ytk)},
t=1,2,…,T.
(Xt,Yt)={(xt1,yt1),(xt2,yt2),…,(xtk,ytk)},
t=1,2,…,T,
可以通过最小二乘法得
(7)
上式中
(8)
(9)
3 基于电梯停靠楼层识别问题的算法
3.1 回归模型参数学习算法在电梯停靠楼层识别中,面临着训练模型的带标签数据量不够的问题,为了解决该问题,本文提出了基于回归分析的参数调整方法.
本文将训练模型的数据分为两个部分:一部分为大气压值与其对应的楼层的带标签的训练数据;另一部分为定时采集、数据量较少、用于参数调整的不带标签的大气压训练数据.
在实际工程中,由于用于训练的数据量较少且存在温差不定、相对海拔不同等问题,使得一般的回归模型泛化能力较差.如果关注临时采集的数据所蕴含的信息,会造成模型参数的偏差,不易通过假设检验,无法准确预测电梯停靠楼层.本文通过事先采集到的大气压值及其对应的楼层数据训练模型的初始参数,在假设条件1)和2)下,可以通过实验验证,回归系数β1不会产生改变,只需要调整外部扰动β0,以此适应外部环境的变化,显示未知变量造成的影响.
下面给出建立回归模型的算法:

输入:n组训练集数据(x1,y1),(x2,y2),…,(xn,yn).输出:回归模型参数^β0和^β1.㊣Step㊞ 1 进行数据预处理,去除异常数据.㊣Step㊞ 2 建立线性回归模型,进行拟合优度检验,判断Y与X间是否存在线性关系.yi表示停靠楼层,xi表示停靠楼层对应的大气压值.㊣Step㊞ 3 线性回归模型y=β0+β1x+ε,外部扰动ε需满足零均值性、方差齐次性、互不相关性、同期外生性的假设.㊣Step㊞ 4 对模型的参数进行估计,^β0= y-^β1 x,^β1=∑㊞n㊞i=1(x㊞i- x)(y㊞i- y)∑㊞n㊞i=1(x㊞i- x)2, 其中, y=1n∑㊞n㊞i=1yi, x=1n∑㊞n㊞i=1xi.㊣Step㊞ 5 输出β0和β1的估计值^β0和^β1.
3.2 参数自适应算法针对参数调整的3个假设:
1) 楼层间的距离是一样的;
2) 外部环境的改变不会影响大气压与楼层间的相对变化;
3) 大气压相对外部一切随机因素间的变化过程缓慢,在某种意义上说,短时间内认为回归模型可以针对楼层进行准确的识别,长时间会导致回归模型无法进行精准地识别,即t时间的模型可以对t+tmin时间的数据进行准确判断.
参数迭代后的回归模型通过n组事先准备的训练集数据(xi,yi)(i=1,2,…,n)与t时刻的数据(Xt,Yt)={(xt1,yt1),(xt2,yt2),…,(xtk,ytk)}(t=1,2,…,T),对β0和β1进行估计.下面给出参数调整模型的算法:

输入:t时刻的数据Xt=(xt1,xt2,…,xtk).输出:调整后的参数^β'0和^β'1与回归方程.㊣Step㊞ 1 利用t-1时刻的回归模型对输入数据Xt=(xt1,xt2,…,xtk)进行识别得到(X㊞t,Y㊞t)={(x㊞t1,y㊞t1),(x㊞t2,y㊞t2),…,(x㊞tk,y㊞tk)},t=1,2,…,T.㊣Step㊞ 2 计算 yt=1n∑k㊞i=1yti, xt=1n∑k㊞i=1xti.㊣Step㊞ 3 令^β't1=^β1,^β't0= yt-^β'1 xt.㊣Step㊞ 4 得到β0和β1的估计值^β't1和^β't0.㊣Step㊞ 5 输出t时段回归方程:^yt=^β't0+^β't1x.
实际工程项目实施时需要注意该方法收集的数据均为在楼层停靠时收集,在电梯运行过程中,收集数据会导致模型识别失效.
具体的模型参数自适应方法如图1所示.
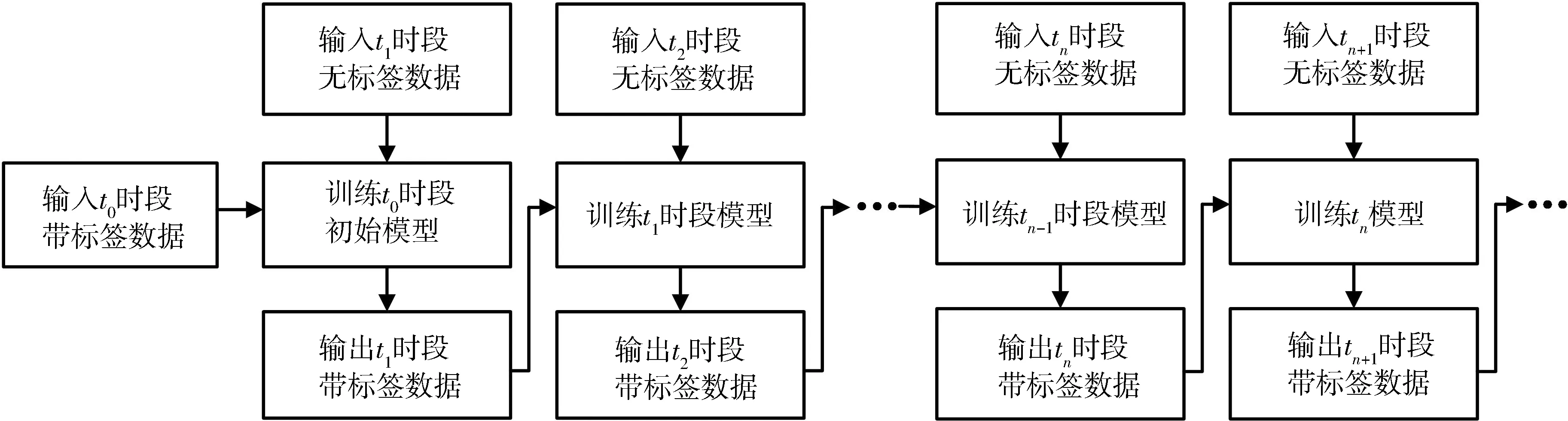
图1 参数自适应模型
3.3 不严格满足假设的情况在实际情况中,存在部分楼层的底层间距较大的情况,假设1)不是严格满足的.在这种情况下,本文的方法稍加修改即可满足,即将二楼作为参与迭代最低楼层,并设置气压最低阈值,当气压小于该阈值时,因变量目标楼层显示为1楼,阈值记为α.
下面给出此情况下的算法:

输入:n组训练集数据(x1,y1),(x2,y2),…,(xn,yn)、t时刻的数据Xt=(xt1,xt2,…,xtk).输出:t时刻的数据Xt对应的Yt=(yt1,…,ytk).㊣Step㊞ 1 在在所有数据中删除y=1的所有数据,令其他所有y=y-1.㊣Step㊞ 2 建立回归模型.㊣Step㊞ 3 计算t时刻调整后的参数^β'0、^β'1和回归方程^yt=^β't0+^β't1x.㊣Step㊞ 4 计算阈值α=^β't0+^β't1(1-1)=^β't0.㊣Step㊞ 5 计算yt=1, xt<α;^β't0+^β't1x+1, xt≥α.
4 结果验证与分析
本文使用的数据均来自于四川省成都市西南交通大学内部教学楼、宿舍楼实时采集的气压值数据,数据采集的时间间隔为每秒1次.为验证该方法,在西南交通大学犀浦校区3号教学楼以及鸿哲斋9栋,共进行50次实验.本节展示在西南交通大学犀浦校区3号教学楼进行的部分实验.
4.1 确定初始回归参数随机选择n个楼层的大气压值数据进行采集,以拟合初始参数,采集到的部分大气压数据如表1所示.
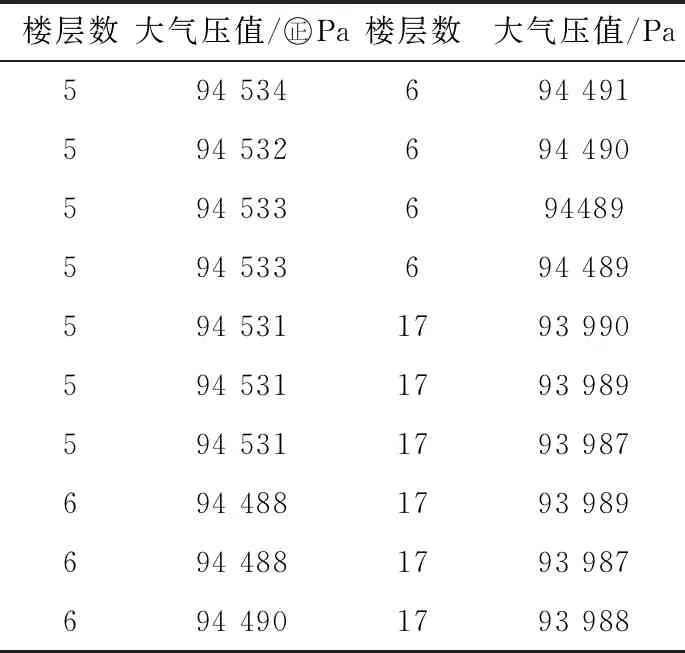
表1 初始数据
为了方便计算与分析,对采集到的大气压数值进行变换:x=x-90 000,对数据进行拟合,得到回归方程
y1=-0.022 661x1+107.456 655.
4.2 模型显著性检验对模型进行F检验和拟合优度检验,得到结果如表2所示.

表2 模型的检验
4.3 参数迭代若参数迭代时间间隔较短,则计算量过大,不易于实际工程实施;若迭代时间间隔较长,则t时段模型无法准确识别t+1时段电梯停靠楼层,经实地实验验证,时间间隔为4min为在保证模型识别准确率的情况下的最大时间间隔.

表3 参数迭代过程
4.4 结果分析对第50个时段的数据进行分析,部分结果如表4所示.

表4 模型判别结果

图2 楼层识别结果

图3 楼层识别结果
图4是不同监督模型对楼层识别的准确率对比图.在图4中可以发现在短时间40min内,线性回归、多分类Logistic回归和多分类SVM(support vector machines,支持向量机)[21-22]的识别准确率也达到了100%.但是由于监督学习模型的特点,模型由训练集数据训练完毕,对目标识别判断的规则不会进行改变,即无法感知外部环境的变化并做出相应的调整.这导致上述的模型进过一段时间后,识别准确率急速下降,最后完全无法对楼层进行正确的识别.
5 结论
本文直接建立大气压与电梯停靠楼层之间的关系,利用短时间内模型对楼层正确识别的能力,将短时间内无标签的大气压值,识别出其对应的楼层,从而获得带标签数据.再利用最小二乘法思想,使用识别后的带标签数据对模型的参数进行自适应迭代调整,保证了模型长时间也可以进行正确的目标识别.
在实验验证中,通过基于参数自适应的回归模型与线性回归模型进行对照实验,发现普通的线性回归模型在20min左右开始出现错误,在30min时无法对目标进行准确的识别;而基于参数自适应的回归模型可以长时间对目标进行准确识别,识别的正确率为100%.特别地,在测试时间增加的情况下,普通的回归模型会出现无规律错误,无法通过数值的增减简单改进.当昼夜温差较大时,普通的监督学习模型由于没有对外部环境的感知能力,导致楼层识别出现错误.本模型的特性是根据外部环境进行参数自适应迭代,充分考虑外部环境变化产生的影响.虽然昼夜温差较大,但是温度短时间内不会急剧变化,依照模型假设条件,本模型可以有效地针对外部环境的变化,进行参数的自适应调整,保持识别的正确率.实验结果表明,基于参数自适应的回归模型具有较好的泛化能力,对温度、湿度、楼梯间通风情况等因素不敏感,能够较好地适用于工程项目.
6 研究展望
当楼层高度不是一致时,可以使用分段式回归模型,用同样的方法考虑外部扰动造成的影响,针对更普适的情况进行楼层识别.
本文实验的数据仅采集了大气压数据,为一维数据,在数据维数变高时,怎样解决更一般的问题.本文的思想是通过t时刻的数据对t+1时刻的模型进行调整,运用这种思想是否可以应用到更一般的模型.对上述两个方面进行深入研究可以作为下一步的研究计划.

