剩余格的模糊滤子理论
刘春辉(赤峰学院数学与统计学院,内蒙古赤峰024001)
剩余格的模糊滤子理论
刘春辉
(赤峰学院数学与统计学院,内蒙古赤峰024001)
运用模糊集的方法和原理进一步深入研究剩余格的滤子问题.在剩余格中引入了模糊预线性滤子,模糊可除滤子和模糊G livenko滤子三类新的模糊滤子概念,给出了它们的若干性质和等价刻画.系统讨论了这三类模糊滤子以及模糊正关联滤子,模糊Boolean滤子,模糊MV滤子和模糊正则滤子间的相互关系,证明了一个模糊滤子为模糊MV滤子当且仅当它既是模糊正则滤子又是模糊可除滤子的结论.
剩余格;模糊滤子;模糊预线性滤子;模糊可除滤子;模糊G livenko滤子
1 引言
非经典数理逻辑理论是人工智能领域处理不确定信息的重要工具,其主要研究方向之一是对与各种逻辑系统相匹配的逻辑代数系统的研究,相关的研究成果既促进了非经典数理逻辑理论的发展,又丰富了代数学的内容[1].在为数众多的非经典逻辑代数系统中,由Ward和Dilworth于上个世纪30年代在文献[2]中首次提出的剩余格是一类重要且应用广泛的代数系统,它是Heyting代数的合理推广.Pavelka以Lukasiew icz公理系统为背景,将剩余理论引入到非经典数理逻辑的研究中,建立了一类相当宽泛的逻辑结构,并以此为基础,成功地解决了Lukasiew icz公理系统的语义完备性问题[3].目前,剩余格已经被学者们公认为一类重要的非经典数理逻辑代数结构,是模糊逻辑中相当理想的代数框架,诸如M TL代数,BL代数,MV代数,Rℓ模和G livenko代数等著名的逻辑代数系统都是其特殊子类,因此对剩余格结构的深入研究具有广泛而基本的重要意义,相关研究成果也颇为丰富[4-10].
众所周知,滤子是非经典逻辑代数研究领域的一个重要的概念,它们对各种逻辑系统及与之匹配的逻辑代数的完备性问题的研究发挥着极其重要的作用.因此,这方面的研究工作一直深受学者们的广泛关注[11-18].其中,文献[14]在剩余格中引入了布尔滤子和正关联滤子的概念并研究了它们的性质.文献[15]又在剩余格中引入了MV-滤子和正则滤子等概念,较为深入地研究了它们的特性和模糊化问题,并讨论了各类滤子概念间的相互关系.文献[16-18]对剩余格的滤子及其模糊化问题作了更进一步的研究和探讨.在上述工作的基础上,本文进一步深入系统地研究剩余格的模糊滤子问题,给出了剩余格的模糊正关联滤子,模糊Boolean滤子,模糊MV-滤子和模糊正则滤子的若干新的等价刻画.引入模糊预线性滤子,模糊可除滤子和模糊Glivenko滤子几类新的概念,考察了它们的性质和等价刻画,并利用它们的性质获得了几类特殊剩余格的特征定理.最后,系统梳理了各类模糊滤子概念间的相互关系.获得了一些有意义的结果.进一步丰富和完善了剩余格的滤子问题的理论体系.
2 预备知识
定义2.1[2,4,10,15](i)称(2,2,2,2,0,0)型代数(L,≤,∧,∨,⊗,→,0,1)为一个剩余格,简称L为一个剩余格,如果下列各条件成立:
(RL1)(L,∧,∨,0,1)是分别以0和1为最小元和最大元的有界格;
(RL2)(L,⊗,1)是一个以1为单位元的交换半群;
(RL3)(⊗,→)是L上的伴随对,即(∀x,y,z∈L)(x⊗y≤z⇔x≤y→z).
(ii)称剩余格L为一个预线性剩余格,如果L满足:(∀x,y∈L)((x→y)∨(y→x)=1).
(iii)称剩余格L为一个可除剩余格,如果L满足:(∀x,y∈L)(x∧y=x⊗(x→y)).
(iv)称剩余格L为一个正则剩余格,如果L满足:(∀x∈L)(x′′=x).其中x′=x→0.
(v)称剩余格L为一个G livenko代数,如果L满足:(∀x∈L)((x′′→x)′′=1).
(vi)称剩余格L为一个BL代数,如果L为可除的预线性剩余格.
(vii)称剩余格L为一个MV代数,如果L为可除的正则剩余格[15].
引理2.1[2-10,14-18]设L是剩余格,则下列各条件成立:
(RL4)(∀x,y∈L)(x≤y⇔x→y=1);
(RL5)(∀x∈L)(x→x=1,x→1=1,1→x=x);
(RL6)(∀x,y∈L)(y≤x→y,x∨y≤(x→y)→y);
(RL7)(∀x,y∈L)(x⊗y≤x⊗(x→y)≤x∧y≤x∧(x→y)≤x);
(RL8)(∀x,y,z∈L)((x→y)→z≤x→(y→z));
(RL9)(∀x,y∈L)(x⊗(x→y)≤y≤x→(x⊗y));
(RL10)(∀x,y,z∈L)((x→y)⊗(y→z)≤x→z);
(RL11)(∀x,y,z∈L)((x≤y)⇒(x⊗z≤y⊗z,z→x≤z→y,y→z≤x→z));
(RL12)(∀x,y,z∈L)(x→(y→z)=(x⊗y)→z=y→(x→z));
(RL13)(∀x,y,z∈L)((y∨z)⊗x=(y⊗x)∨(z⊗x),x∨(y⊗z)≥(x∨y)⊗(x∨z));
(RL14)(∀x,y,z∈L)((y∨z)→x=(y→x)∧(z→x),特别地:(y∨z)→y=z→y);
(RL15)(∀x,y,z∈L)(x→(y∧z)=(x→y)∧(x→z),特别地:y→(y∧z)=y→z);
(RL16)(∀x,y,z∈L)(x→(y∨z)≥(x→y)∨(x→z),(y∧z)→x≥(y→x)∨(z→x));
(RL17)(∀x,y,z∈L)(y→z≤(x→y)→(x→z)≤x→(y→z));
(RL18)(∀x,y,z∈L)(x→y≤(y→z)→(x→z));
(RL19)(∀x,y∈L)(((x→y)→y)→y=x→y);
(RL20)(∀x,y,z∈L)(x⊗(y→z)≤y→(x⊗z)≤(x⊗y)→(x⊗z));
(RL21)(∀x,y,z∈L)((y→x)⊗((x∧y)→z)≤(y→(x∧y))∧(y⊗z));
(RL22)(∀x,y,z,w∈L)((x→y)⊗(z→w)≤(x∨z)→(y∨w));
(RL23)(∀x,y,z,w∈L)((x→y)⊗(z→w)≤(x∧z)→(y∧w));

定义2.2[16-17]设L是剩余格,∅/=F⊆L.称F为L的滤子,若F满足
(F1)(∀x,y∈L)((x∈F且x≤y)⇒y∈F);
(F2)(∀x,y∈L)((x∈F且y∈F)⇒x⊗y∈F).
引理2.2[16-17]设L是剩余格,∅/=F⊆L.则F为L的滤子当且仅当F满足
(F3)1∈F;
(F4)(∀x,y∈L)((x∈F且x→y∈F)⇒y∈F).
定义2.2[16,18]设L是剩余格,f:L→[0,1]为L上的模糊集.称f为L的模糊滤子,若f满足
(FF1)(∀x,y∈L)(x≤y⇒f(y)≥f(x));
(FF2)(∀x,y∈L)(f(x⊗y)≥f(x)∧f(y)).
注2.1设L是剩余格,f为L的模糊滤子,则对任意的x,y∈L有f(x)=f(y)=f(1)⇔f(x∧y)=f(1)⇔f(x⊗y)=f(1)⇔f(x⊗(x→y))=f(1).
引理2.3[16]设L是剩余格,f为L上的模糊集.则f为L的模糊滤子当且仅当f满足
(FF3)(∀x∈L)(f(1)≥f(x));
(FF4)(∀x,y∈L)(f(y)≥f(x)∧f(x→y)).
引理2.4[16]设L是剩余格,f为L上的模糊集.则f为L的模糊滤子当且仅当f满足
(FF5)(∀x,y,z∈L)(x⊗y≤z⇒f(z)≥f(x)∧f(y)).
3 剩余格的几类特殊模糊滤子的新刻画
定义3.1[12,15]设L是剩余格,f为L的模糊滤子.称f为L的模糊正关联滤子,若f满足
(FP)(∀x,y,z∈L)(f(x→z)≥f(x→(y→z))∧f(x→y)).
注3.1在文献[15]和众多相关文献中,模糊正关联滤子也称为模糊G-滤子.关于模糊正关联滤子的等价刻画请参阅文献[12]定理2.5和文献[15]定理4.21.
定理3.1设L是剩余格,f为L的模糊滤子.则下列各条件等价:
(1)f是L的模糊正关联滤子;
(2)(∀x,y∈L)(f((x∧(x→y))→y)=f(1));
(3)(∀x,y∈L)(f((x∧y)→(x⊗y))=f(1));
(4)(∀x,y∈L)(f((x∧(x→y))→(x⊗y))=f(1));
(5)(∀x,y∈L)(f((x⊗(x→y))→(x⊗y))=f(1));
(6)(∀x,y∈L)(f((x∧(x→y))→(x∧y))=f(1));
(7)(∀x,y∈L)(f((x∧(x→y))→(x⊗(x→y)))=f(1));
(8)(∀x,y∈L)(f((x∧(x→y))→(y∧(y→x)))=f(1)).
证(1)⇒(2):设f是L的模糊正关联滤子.任取x,y∈L,因为x∧(x→y)≤x→y且x∧(x→y)≤x,所以由(RL4)得(x∧(x→y))→(x→y)=1且(x∧(x→y))→x=1.故由(FP)得f((x∧(x→y))→y)≥f((x∧(x→y))→(x→y))∧f((x∧(x→y))→x)= f(1)∧f(1)=f(1),因此结合(FF3)便得f((x∧(x→y))→y)=f(1),即(2)成立.
(2)⇒(3):设(2)成立,则∀x,y∈L,f((x∧(x→(x⊗y)))→(x⊗y))=f(1).又因为由(RL9)得y≤x→(x⊗y),所以x∧y≤x∧(x→(x⊗y)),从而由(RL11)得(x∧y)→(x⊗y)≥(x∧(x→(x⊗y)))→(x⊗y).故由(FF1)得f((x∧y)→(x⊗y))≥f((x∧(x→(x⊗y)))→(x⊗y))=f(1),因此结合(FF3)便得f((x∧y)→(x⊗y))=f(1),即(3)成立.
(3)⇒(4):设(3)成立,则∀x,y∈L,f((x∧(x→y))→(x⊗(x→y)))=f(1).因为由(RL7)得x⊗(x→y)≤x∧y,所以由(RL11)得(x∧(x→y))→(x⊗(x→y))≤(x∧(x→y))→(x∧y),故由(FF1)得f((x∧(x→y))→(x∧y))≥f((x∧(x→y))→(x⊗(x→y)))=f(1).又因为由(RL10)得((x∧(x→y))→(x∧y))⊗((x∧y)→(x⊗y))≤(x∧(x∧y))→(x⊗y),所以由(FF1),(FF2)和(3)便得f((x∧(x∧y))→(x⊗y))≥f(((x∧(x→y))→(x∧y))⊗((x∧y)→(x⊗y)))≥f((x∧(x→y))→(x∧y))∧f((x∧y)→(x⊗y))=f(1)∧f(1)=f(1),因此结合(FF3)便得f((x∧(x∧y))→(x⊗y))=f(1),即(4)成立.
(4)⇒(5):设(4)成立.任取x,y∈L,因为由(RL7)得x⊗(x→y)≤x∧(x→y),所以由(RL11)得(x⊗(x→y))→(x⊗y)≥(x∧(x→y))→(x⊗y).故由(FF1)和(4)得f((x⊗(x→y))→(x⊗y))≥f((x∧(x→y))→(x⊗y))=f(1),因此结合(FF3)便得f((x⊗(x→y))→(x⊗y))=f(1),即(5)成立.
(5)⇒(1):设(5)成立.则在(5)中取y=x并利用(RL12)和(RL5)便得f(1)=f((x⊗(x→x))→(x⊗x))=f((x⊗1)→(x⊗x))=f(x→(1→(x⊗x)))=f(x→(x⊗x)).因此由文献[15]定理4.21便得f是L的模糊正关联滤子,即(1)成立.
(4)⇒(6)⇒(7)⇒(8):设(4)成立.任取x,y∈L,因为由(RL7)得x⊗y≤x⊗(x→y)≤x∧y≤y∧(y→x),所以由(RL11)得(x∧(x→y))→(x⊗y)≤(x∧(x→y))→(x⊗(x→y))≤(x∧(x→y))→(x∧y)≤(x∧(x→y))→(y∧(y→x)).故由(FF1)和(4)得f((x∧(x→y))→(y∧(y→x)))≥f((x∧(x→y))→(x∧y))≥f((x∧(x→y))→(x⊗(x→y)))≥f((x∧(x→y))→(x⊗y))=f(1).因此结合(FF3)得f((x∧(x→y))→(x∧y))=f(1)且f((x∧(x→y))→(x⊗(x→y)))=f(1)且f((x∧(x→y))→(y∧(y→x)))=f(1),即(4)⇒(6)⇒(7)⇒(8)成立.
(8)⇒(3):设(8)成立.任取x,y,z∈L,因为由(RL7)得(x⊗z)∧((x⊗z)→x)≤x⊗z,所以由(RL11)得(x∧(x→(x⊗z)))→((x⊗z)∧((x⊗z)→x))≤(x∧(x→(x⊗z)))→(x⊗z).故由(FF1)和(8)得f((x∧(x→(x⊗z)))→(x⊗z))≥f((x∧(x→(x⊗z)))→((x⊗z)∧((x⊗z)→x)))=f(1).又因为由(RL9)得z≤x→(x⊗z),所以x∧z≤x∧(x→(x⊗z)),从而由(RL11)得(x∧z)→(x⊗z)≥(x∧(x→(x⊗z)))→(x⊗z).故再由(FF1)得f((x∧z)→(x⊗z))≥f((x∧(x→(x⊗z)))→(x⊗z))≥f(1),因此结合(FF3)便得f((x∧z)→(x⊗z))=f(1),即(3)成立.综上,定理得证.
定义3.2[12,15]设L是剩余格,f为L的模糊滤子.称f为L的模糊Boolean滤子,若f满足
(FB)(∀x∈L)(f(x∨x′)=f(1)).
注3.2在文献[15]和众多相关文献中,模糊Boolean滤子也称为模糊关联滤子.关于模糊Boolean滤子的等价刻画请参阅文献[12]定理2.4及文献[15]定理4.12和推论4.13.
定理3.2设L是剩余格,f为L的模糊滤子.则下列各条件等价:
(1)f是L的模糊Boolean滤子;
(2)(∀x∈L)(f(x∨(x→y))=f(1));
(3)(∀x,y∈L)(f(((x→y)→x)→x)=f(1));
(4)(∀x∈L)(f((x′→x)→x)=f(1));
(5)(∀x,y,z∈L)(f((((x∨y)→z)→y)→(x∨y))=f(1));
(6)(∀x,y∈L)(f(((x∨y)′→y)→(x∨y))=f(1)).
证(1)⇒(2):设f是L的模糊Boolean滤子.任取x,y∈L,因为0≤y,所以由(RL11)得x′= x→0≤x→y,从而x∨x′≤x∨(x→y).故由(FF1)和(FB)得f(x∨(x→y))≥f(x∨x′)=f(1).因此结合(FF3)便得f(x∨(x→y))=f(1),即(2)成立.
(2)⇒(3):设(2)成立.任取x,y∈L,因为由(RL6)得x∨(x→y)≤((x→y)→x)→x,所以由(FF1)和(2)得f(((x→y)→x)→x)≥f(x∨(x→y))=f(1).因此结合(FF3)便得f(((x→y)→x)→x)=f(1),即(3)成立.
(3)⇒(4):设(3)成立.则在(3)中取y=0便得f(1)=f(((x→0)→x)→x)=f((x′→x)→x),即(4)成立.
(4)⇒(1):设(4)成立.任取x∈L,一方面,由(FF4),(4)和(FF3)得f(x)≥f((x′→x)→x)∧f(x′→x)=f(1)∧f(x′→x)=f(x′→x).另一方面,因为由(RL6)得x≤x′→x,所以由(FF1)又得f(x′→x)≥f(x).故综合两方面便得f(x)=f(x′→x).因此由文献[15]定理4.12(2)得f是L的模糊Boolean滤子.
(3)⇒(5):设(3)成立.任取x,y,z∈L,因为由(RL5)和(RL4)得x∨y=1→(x∨y)=(y→(x∨y))→(x∨y)且由(RL10)得(((x∨y)→z)→y)⊗(y→(x∨y))≤((x∨y)→z)→(x∨y),所以由(RL12)和(RL11)得故由(FF1)和(3)得f((((x∨y)→z)→y)→(x∨y))≥f((((x∨y)→z)→(x∨y))→(x∨y))= f(1),因此结合(FF3)便得f((((x∨y)→z)→y)→(x∨y))=f(1),即(5)成立.

(5)⇒(6):设(5)成立.在(5)中取z=0便得f(1)=f((((x∨y)→0)→y)→(x∨y))= f(((x∨y)′→y)→(x∨y)),即(6)成立.
(6)⇒(4):设(6)成立.在(6)中取y=x便得f(1)=f(((x∨x)′→x)→(x∨x))=f((x′→x)→x),即(4)成立.综上,定理得证.
定义3.3[12,15]设L是剩余格,f为L的模糊滤子.称f为L的模糊MV滤子,若f满足
(FMV)(∀x,y∈L)(f(((x→y)→y)→x)≥f(y→x)).
注3.3在文献[15]和相关文献中,模糊MV滤子也称为模糊fantastic滤子或模糊交换滤子.关于模糊MV滤子的等价刻画请参阅文献[15]中注4.23,定理4.24和定理4.25.
定理3.3设L是剩余格,f为L的模糊滤子.则下列各条件等价:
(1)f是L的模糊MV滤子;
(2)(∀x,y∈L)(f(((x→y)→y)→(x∨y))=f(1)).

(2)⇒(1):设(2)成立.任取x,y∈L,因为由(RL6)得x∨y≤(y→x)→x,所以由(RL11)可得((x→y)→y)→(x∨y)≤((x→y)→y)→((y→x)→x),故由(FF1)和(2)便得f(((x→y)→y)→((y→x)→x))≥f(((x→y)→y)→(x∨y))=f(1),再结合(FF3)得f(((x→y)→y)→((y→x)→x))=f(1).因此由文献[15]中定理4.25便得f是L的模糊MV滤子.定理得证.
定义3.4[15]设L是剩余格,f为L的模糊滤子.称f为L的模糊正则滤子,若f满足
(FR)(∀x∈L)(f(x′′→x)=f(1)).
注3.4模糊正则滤子的等价刻画请参阅文献[15]定理5.14,注5.15,定理5.17和定理5.18.
定理3.4设L是剩余格,f为L的模糊滤子.则下列各条件等价:
(1)f是L的模糊正则滤子;
(2)(∀x,y∈L)(f((y′→x′)→(x→y)))=f(1));
(3)(∀x,y∈L)(f((y′→x)→(x′→y)))=f(1)).
证(1)⇒(2):设f是L的模糊正则滤子.任取x,y∈L,因为由(RL29),(RL28)和(RL11)可得y′→x′≤x′′→y′′≤x→y′′,所以由(RL11)和(RL17)得(y′→x′)→(x→y)≥(x→y′)→(x→y)≥y′′→y.故由(FF1)和(FR)得f((y′→x′)→(x→y))≥f(y′′→y)=f(1),因此结合(FF3)便得f((y′→x′)→(x→y))=f(1),即(2)成立.
(2)⇒(1):设(2)成立.任取x,y∈L,由引理2.3和(2)得f(x→y)≥f((y′→x′)→(x→y))∧f(y′→x′)=f(1)∧f(y′→x′)=f(y′→x′),故由文献[15]定理5.14得f是模糊正则滤子.
(1)⇒(3):设f是L的模糊正则滤子.任取x,y∈L,因为由(RL29)可得y′→x≤x′→y′′,所以由(RL11)和(RL17)得(y′→x)→(x′→y)≥(x′→y′′)→(x′→y)≥y′′→y.故由(FF1)和(FR)得f((y′→x)→(x′→y))≥f(y′′→y)=f(1),因此结合(FF3)便得f((y′→x)→(x′→y))=f(1),即(3)成立.
(3)⇒(1):设(3)成立.任取x,y∈L,由引理2.3和(2)得f(x′→y)≥f((y′→x)→(x′→y))∧f(y′→x)=f(1)∧f(y′→x)=f(y′→x),故由文献[15]定理5.14得f是L的模糊正则滤子.
4 剩余格的几类新型模糊滤子及其特征
本节我们将在剩余格中引入三类新型的模糊滤子概念并考察它们的性质特征.
定义4.1设L是剩余格,f为L的模糊滤子.称f为L的模糊预线性滤子,若f满足
(FPL)(∀x,y∈L)(f((x→y)∨(y→x))=f(1)).
定理4.1设L是剩余格,f为L的模糊滤子.则下列各条件等价:
(1)f是L的模糊预线性滤子;
(2)(∀x,y,z∈L)(f((x→y)∨(x→z))≥f(x→(y∨z)));
(3)(∀x,y,z∈L)(f((x→(y∨z))→((x→y)∨(x→z)))=f(1));
(4)(∀x,y,z∈L)(f((y→x)∨(z→x))≥f((y∧z)→x));
(5)(∀x,y,z∈L)(f(((y∧z)→x)→((y→x)∨(z→x)))=f(1));
(6)(∀x,y,z∈L)(f((x→y)∨(y→z))≥f(x→z));
(7)(∀x,y,z∈L)(f((x→z)→((x→y)∨(y→z)))=f(1));
(8)(∀x,y,z∈L)(f(((y→x)→z)→z)≥f((x→y)→z));
(9)(∀x,y,z∈L)(f(((x→y)→z)→(((y→x)→z)→z))=f(1)).
证(1)⇒(2):设f是L的模糊预线性滤子.∀x,y,z∈L,因为由(RL13),(RL14)和(RL10)可得(x→(y∨z))⊗((y→z)∨(z→y))=((x→(y∨z))⊗(y→z))∨((x→(y∨z))⊗(z→y))=((x→(y∨z))⊗((y∨z)→z))∨((x→(y∨z))⊗((y∨z)→y))≤(x→z)∨(x→y).故由定义2.3,(FPL)和(FF3)得f((x→z)∨(x→y))≥f((x→(y∨z))⊗((y→z)∨(z→y)))≥f(x→(y∨z))∧f((y→z)∨(z→y))=f(x→(y∨z))∧f(1)=f(x→(y∨z)).即(2)成立.
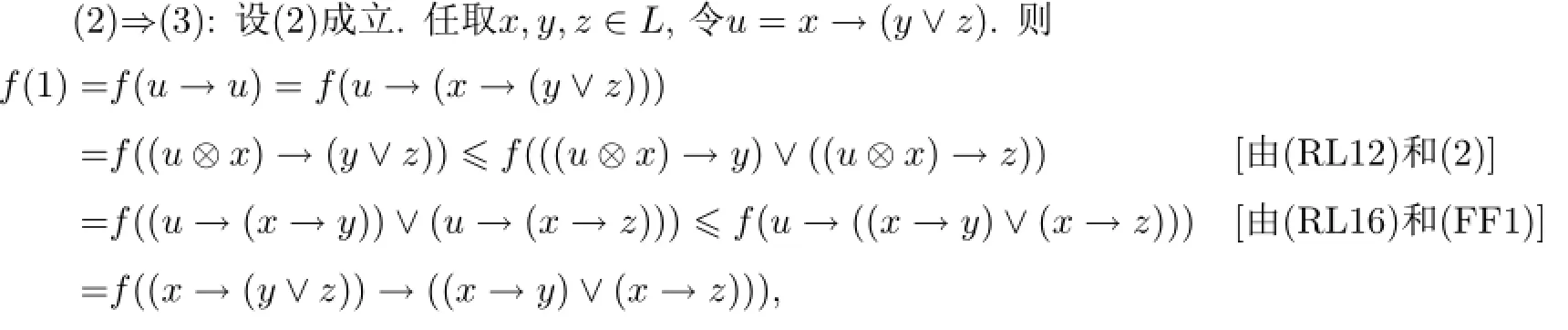
因此结合(FF3)便得f((x→(y∨z))→((x→y)∨(x→z)))=f(1),即(3)成立.
(3)⇒(1):设(3)成立.任取y,z∈L,在(3)中取x=y∨z,则由(RL14)和(RL5)得f(1)= f(((y∨z)→(y∨z))→(((y∨z)→y)∨((y∨z)→z)))=f(1→((z→y)∨(y→z)))= f((z→y)∨(y→z)),即(FPL)成立,因此由定义4.1得f是L的模糊预线性滤子.
(1)⇒(4):设f是L的模糊预线性滤子.∀x,y,z∈L,因为由(RL13),(RL14)和(RL10)可得((y∧z)→x)⊗((y→z)∨(z→y))=(((y∧z)→x)⊗(y→z))∨(((y∧z)→x)⊗(z→y))=(((y∧z)→x)⊗(y→(y∧z)))∨(((y∧z)→x)⊗(z→(y∧z)))≤(y→x)∨(z→x).故由定义2.3,(FPL)和(FF3)得f((y→x)∨(z→x))≥f(((y∧z)→x)⊗((y→z)∨(z→y)))≥f((y∧z)→x)∧f((y→z)∨(z→y))=f((y∧z)→x)∧f(1)=f((y∧z)→x).即(4)成立.
(4)⇒(5):设(4)成立.任取x,y,z∈L,令u=(y∧z)→x.则

因此结合(FF3)便得f(((y∧z)→x)→((y→x)∨(z→x)))=f(1),即(5)成立.
(5)⇒(1):设(5)成立.任取y,z∈L,在(3)中取x=y∧z,则由(RL15)和(RL5)得f(1)= f(((y∧z)→(y∧z))→((y→(y∧z))∨(z→(y∧z))))=f(1→((y→z)∨(z→y)))= f((y→z)∨(z→y)),即(FPL)成立,因此由定义4.1得f是L的模糊预线性滤子.
(1)⇒(6):设f是L的模糊预线性滤子.∀x,y,z∈L,因为由(RL13),(RL7)和(RL10)得(x→z)⊗((x→y)∨(y→x))=((x→z)⊗(x→y))∨((x→z)⊗(y→x))≤(x→y)∨(y→z),故由定义2.3,(FPL)和(FF3)得f((x→y)∨(y→z))≥f((x→z)⊗((x→y)∨(y→x)))≥f(x→z)∧f((x→y)∨(y→x))=f(x→z)∧f(1)=f(x→z),即(6)成立.
因此结合(FF3)便得f((x→z)→((x→y)∨(y→z)))=f(1),即(7)成立.
(7)⇒(1):设(7)成立.任取x,y∈L,在(3)中取z=x,则由(RL5)得f(1)=f((x→x)→((x→y)∨(y→x)))=f(1→((x→y)∨(y→x)))=f((x→y)∨(y→x)),即(FPL)成立,因此由定义4.1得f是L的模糊预线性滤子.
(1)⇒(8):设f是L的模糊预线性滤子.∀x,y,z∈L,因为由(RL12),(RL11)和(RL14)得((x→y)→z)→(((y→x)→z)→z)=(((x→y)→z)⊗((y→x)→z))→z≥(((x→y)→z)∧((y→x)→z))→z=(((x→y)∨(y→x))→z)→z≥(x→y)∨(y→x),所以定义2.3,(FPL)和(FF3)得f(((y→x)→z)→z)≥f(((x→y)→z)→(((y→x)→z)→z))∧f((x→y)→z)≥f((x→y)∨(y→x))∧f((x→y)→z)=f(1)∧f((x→y)→z)=f((x→y)→z).因此(8)成立.
因此结合(FF3)便得f(((x→y)→z)→(((y→x)→z)→z))=f(1),即(9)成立.
(9)⇒(1):设(9)成立.任取x,y∈L,在(3)中取z=(x→y)∨(y→x),则由(RL5)得f(1)= f(((x→y)→((x→y)∨(y→x)))→(((y→x)→((x→y)∨(y→x)))→((x→y)∨(y→x))))=f(1→(1→((x→y)∨(y→x))))=f((x→y)∨(y→x)),即(FPL)成立,因此由定义4.1得f是L的模糊预线性滤子.综上,定理得证.
定理4.2设L是剩余格.则下列各条件等价:
(1)L是预线性剩余格;
(2)L的任一模糊滤子都是L的模糊预线性滤子;
(3)χ{1}是L的模糊预线性滤子.
证(1)⇒(2)⇒(3):由定义2.1和定义4.1显然成立.
(3)⇒(1):设χ{1}是L的模糊预线性滤子,则对任意的x,y∈L,χ{1}((x→y)∨(y→x))= χ{1}(1)=1,故(x→y)∨(y→x)=1.因此L是预线性剩余格.定理得证.
定义4.2设L是剩余格,f为L的模糊滤子.称f为L的模糊可除滤子,若f满足
(FD)(∀x,y∈L)(f((x∧y)→(x⊗(x→y)))=f(1)).
定理4.3设L是剩余格,f为L的模糊滤子.则下列各条件等价:
(1)f是L的模糊可除滤子;
(2)(∀x,y,z∈L)(f((x→(y∧z))→((x→y)⊗((x∧y)→z)))=f(1));
(3)(∀x,y,z∈L)(f((y⊗(y→x))→(x⊗(x→y)))=f(1)).
证(1)⇒(2):设f是L的模糊可除滤子.任取x,y,z∈L,则由(RL15)和(FD)得f((x→(y∧z))→((x→y)⊗((x→y)→(x→z))))=f(((x→y)∧(x→z))→((x→y)⊗((x→y)→(x→z))))=f(1).又因为由(RL18)和(R l26)得(x∧y)→(x⊗(x→y))≤((x⊗(x→y))→z)→((x∧y)→z)≤((x→y)⊗((x⊗(x→y))→z))→((x→y)⊗((x∧y)→z)),所以由(FF1)和(FD)又得f(((x→y)⊗((x⊗(x→y))→z))→((x→y)⊗((x∧y)→z)))≥f((x∧y)→(x⊗(x→y)))=f(1).故由(RL10)和(FF2)便得f((x→(y∧z))→((x→y)⊗((x∧y)→z)))≥f(((x→(y∧z))→((x→y)⊗((x→y)→(x→z))))⊗(((x→y)⊗((x⊗(x→y))→z))→((x→y)⊗((x∧y)→z))))≥f((x→(y∧z))→((x→y)⊗((x→y)→(x→z))))∧f(((x→y)⊗((x⊗(x→y))→z))→((x→y)⊗((x∧y)→z)))≥f(1)∧f(1)=f(1).因此结合(FF3)便得f((x→(y∧z))→((x→y)⊗((x∧y)→z)))=f(1),即(2)成立.
(2)⇒(1):设(2)成立.在(2)中取x=1,则对任意的y,z∈L,f(1)=f((1→(y∧z))→((1→y)⊗((1∧y)→z)))=f((y∧z)→(y⊗(y→z))),即(FD)成立,因此由定义4.2得f是L的模糊可除滤子.
(1)⇒(3):设f是L的模糊可除滤子.任取x,y∈L,因为由(RL17)得y⊗(y→x)≤y∧x,所以由(RL11)得(y∧x)→(x⊗(x→y))≤(y⊗(y→x))→(x⊗(x→y)).故由(FF1)和(FD)得f((y⊗(y→x))→(x⊗(x→y)))≥f((y∧x)→(x⊗(x→y)))=f(1).因此结合(FF3)便得f((y⊗(y→x))→(x⊗(x→y)))=f(1),即(3)成立.
(3)⇒(1):设(3)成立.任取x,y,z∈L,因为由(3)和(RL15)得f(1)=f((y⊗(y→x))→(x⊗(x→y)))=f((y⊗(y→(x∧y)))→(x⊗(x→(x∧y)))).所以在上式中取y=x∧z便得f(1)=f(((x∧z)⊗((x∧z)→(x∧(x∧z))))→(x⊗(x→(x∧(x∧z)))))=f((x∧z)→(x⊗(x→(x∧z))))=f((x∧z)→(x⊗(x→z))),即(FD)成立,因此由定义4.2得f是L的模糊可除滤子.综上,定理得证.
定理4.4设L是剩余格.则下列各条件等价:
(1)L是可除剩余格;
(2)L的任一模糊滤子都是L的模糊可除滤子;
(3)χ{1}是L的模糊可除滤子.
证(1)⇒(2)⇒(3):由定义2.1和定义4.2显然成立.
(3)⇒(1):设χ{1}是L的模糊可除滤子,则对任意的x,y∈L,χ{1}((x∧y)→(x⊗(x→y)))=χ{1}(1)=1,故(x∧y)→(x⊗(x→y))=1,从而x∧y≤x⊗(x→y).又因为由(RL7)得x⊗(x→y)≤x∧y,所以x∧y=x⊗(x→y).因此L是可除剩余格.定理得证.
定义4.3设L是剩余格,f为L的模糊滤子.称f为L的模糊Glivenko滤子,若f满足
(FGL)(∀x∈L)(f((x′′→x)′′)=f(1)).
定理4.5设L是剩余格,f为L的模糊滤子.则下列各条件等价:
(1)f是L的模糊Glivenko滤子;
(2)(∀x,y∈L)(f((y→x′′)→(y→x)′′)=f(1));
(3)(∀x,y∈L)(f((x→y)→(x′′→y)′′)=f(1));
(4)(∀x,y∈L)(f((x′→y)→(y′→x)′)=f(1)).
证(1)⇒(2):设f是L的模糊G livenko滤子.任取x,y∈L,则

因此结合(FF3)便得f((y→x′′)→(y→x)′′)=f(1),即(2)成立.
(2)⇒(1):设(2)成立.任取x∈L,在(2)中取y=x′′,则由(RL5)可得f(1)=f((x′→x′′)→(x′′→x)′′)=f((x′′→x)′′),即(FGL)成立.因此由定义4.2得f是L的模糊Glivenko滤子.

因此结合(FF3)便得f((x→y)→(x′′→y)′′)=f(1),即(3)成立.
(3)⇒(1):设(3)成立.任取x∈L,在(3)中取y=x,则由(RL5)得f(1)=f((x→x)→(x′′→x)′′)=f((x′′→x)′′),即(FGL)成立.因此由定义4.2得f是L的模糊Glivenko滤子.

因此结合(FF3)便得f((x′→y)→(y′→x)′′)=f(1),即(4)成立.
(4)⇒(1):设(4)成立.任取x∈L,在(3)中取y=x′,则由(RL5)得f(1)=f((x′→x′)→(x′′→x)′′)=f((x′′→x)′′),即(FGL)成立.因此由定义4.2得f是L的模糊Glivenko滤子.
定理4.6设L是剩余格.则下列各条件等价:
(1)L是G livenko代数;
(2)L的任一模糊滤子都是L的模糊Glivenko滤子;
(3)χ{1}是L的模糊G livenko滤子.
证(1)⇒(2)⇒(3):由定义2.1和定义4.3显然成立.

5 剩余格的多种特殊类型模糊滤子间的关系
引理5.1[15]设L是剩余格.则下列各条成立:
(1)L的任一模糊Boolean滤子都是模糊正关联滤子(模糊MV滤子),但反之不真;
(2)L的任一模糊MV滤子都是模糊正则滤子,但反之不真;
(3)L的模糊滤子f是模糊Boolean滤子⇐⇒f既是模糊正关联滤子又是模糊MV(正则)滤子.
例5.1设格L={0,a,b,1}且0≤a≤b≤1,L上二元运算→和⊗的定义如下:

则(L,≤,∧,∨,⊗,→,0,1)是一个剩余格.在L上定义模糊集f:[0,1]→L使f(0)=f(a)=f(b)= β,f(1)=α,其中0≤β<α≤1,可以验证f是L的一个模糊MV滤子,进而为模糊正则滤子,但非L的模糊正关联滤子,这是因为f(b→a)=f(b)=β<α=f(1)=f(b→(b→a)).由此可见,在剩余格上模糊正则滤子和模糊MV滤子不必为模糊正关联滤子.
例5.2设格L={0,a,b,1}且0≤a≤b≤1,L上二元运算→和⊗的定义如下:

则(L,≤,∧,∨,⊗,→,0,1)是一个剩余格.在L上定义模糊集f:[0,1]→L使f(0)=f(a)= β,f(b)=f(1)=α,其中0≤β<α≤1,可以验证f是L的一个模糊正关联滤子,但非L的模糊正则滤子,进而非模糊MV滤子.这是因为f(a′′→a)=f(a)=β<α=f(1).由此可见,在剩余格上模糊正关联滤子既不必为模糊正则滤子也不必为模糊MV滤子.
定理5.1设L是剩余格.则L的任一模糊正关联滤子都是模糊可除滤子,但反之不真.
证设f是L的模糊正关联滤子.任取x,y∈L,因为由(RL7)得x⊗y≤x⊗(x→y),所以由(RL11)得(x∧y)→(x⊗y)≤(x∧y)→(x⊗(x→y)),故由(FF1)和定理3.1(3)得f((x∧y)→(x⊗(x→y)))≥f((x∧y)→(x⊗y))=f(1),再结合(FF3)便得f((x∧y)→(x⊗(x→y)))=f(1),即(FD)成立.因此由定义4.2便得f是L的模糊可除滤子.下面的例5.3说明反之不真.定理得证.
例5.3设格L={0,a,b,1}且0≤a≤b≤1,L上二元运算→和⊗的定义如下:

则(L,≤,∧,∨,⊗,→,0,1)是一个剩余格.在L上定义模糊集f:[0,1]→L使f(0)=f(a)=f(b)= β,f(1)=α,其中0≤β<α≤1,可以验证f是L的一个模糊可除滤子,但非L的模糊正关联滤子.这是因为f(a→(a⊗a))=f(a)=β<α=f(1).
定理5.2设L是剩余格.则L的任一模糊可除滤子都是模糊G livenko滤子,但反之不真.
证设f是L的模糊可除滤子.任取x∈L,因为由(RL26)和(RL29)得(x′′∧x)→(x′′⊗(x′′→x))≤(x′′⊗(x′′→x))′→(x′′∧x)′≤(x′′⊗(x′′⊗(x′′→x))′)→(x′′⊗(x′′∧x)′)≤(x′′⊗(x′′∧x)′)′→(x′′⊗(x′′⊗(x′′→x))′)′,所以由(FF1)和(FD)得f((x′′⊗(x′′∧x)′)′→(x′′⊗(x′′⊗(x′′→x))′)′)≥f((x′′∧x)→(x′′⊗(x′′→x)))=f(1),故结合(FF3)得f((x′′⊗(x′′∧x)′)′→(x′′⊗(x′⊗(x′→x))′)′)=f(1).因为由(RL28)得x≤x′,所以由(RL29)得(x′′⊗(x′′∧x)′)′=(x′′⊗x′)′=x′→x′′=1,从而又得f((x′′⊗(x′′∧x)′)′)=f(1).进而由(RL28)和(FF4)又得
f((x′′⊗(x′′→(x′′→x)′))′)=f((x′⊗(x′⊗(x′′→x))′)′)
≥f((x′′⊗(x′′∧x)′)′)∧f((x′′⊗(x′′∧x)′)′→(x′′⊗(x′′⊗(x′′→x))′)′)=f(1)∧f(1)=f(1),又由(RL10)和(RL17)得x′→(x′′→x)=x′→(x′→x)=(x′→0)→(x′→x)≥0→x=1,所以x′→(x′′→x)=1,从而由(RL4)得x′≤x′′→x,进而由(RL27)得(x′′→x)′≤x′′.

于是再结合(FF3)便得f((x′′→x)′′)=f(1),即(FGL)成立.因此由定义4.3得f是L的模糊G livenko滤子.下面的例5.4说明反之不真,定理得证.
例5.4设格L={0,a,b,c,1}且0≤a≤b≤c≤1,L上二元运算→和⊗的定义如下:
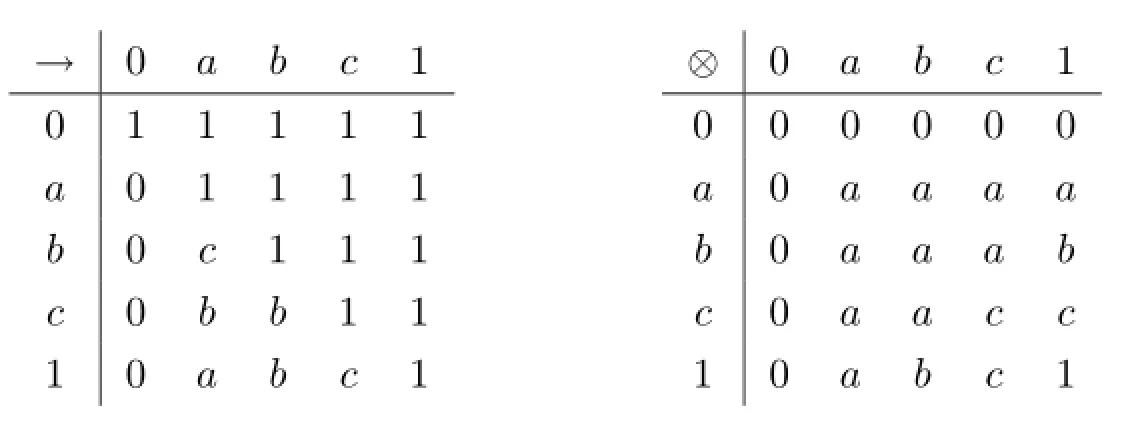
则(L,≤,∧,∨,⊗,→,0,1)是一个剩余格.在L上定义模糊集f:[0,1]→L使f(0)=f(a)=f(b)= f(c)=β,f(1)=α,其中0≤β<α≤1,可以验证f是L的一个模糊Glivenko滤子,但非L的模糊可除滤子.这是因为f((c∧b)→(c⊗(c→b)))=f(c)=β<α=f(1).此外,f也非L的模糊正则滤子,这是因为f(a′′→a)=f(a)=β<α=f(1).这表明:在剩余格中模糊G livenko滤子不必为模糊正则滤子,但由定义3.4和定义4.3易知任一模糊正则滤子必为模糊Glivenko滤子.
定理5.3设L是剩余格.则L的任一模糊MV滤子都是模糊可除滤子,但反之不真.
证设f是L的模糊MV滤子.任取x,y∈L,因为由(RL32),(RL11),(RL33)和(RL29)可得((x′→y′)→y′)→(x′∨y′)≤((x′→y′)→y′)→(x∧y)′=((y→x′′)⊗y)′→(x∧y)′≤(x∧y)′′→((y→x′′)⊗y)′≤(x∧y)→((y→x′′)⊗y)′′,所以由(FF1)和定理3.3得f((x∧y)→((y→x′′)⊗y)′′)≥f(((x′→y′)→y′)→(x′∨y′))=f(1).又模糊MV滤子必为模糊正则滤子,所以由(FR)得f(((y→x′′)⊗y)′′→((y→x′′)⊗y))=f(1).故由(RL10)得f((x∧y)→((y→x′′)⊗y))≥f(((x∧y)→((y→x′′)⊗y)′′)⊗(((y→x′′)⊗y)′′→((y→x′′)⊗y)))≥f((x∧y)→((y→x′′)⊗y)′′)∧f(((y→x′′)⊗y)′′→((y→x′′)⊗y))≥

故结合(FF3)得f((x∧y)→(y⊗(y→x)))=f(1),即(FD)成立.因此由定义4.2便得f是L的模糊可除滤子.反之,考虑例5.3中所给模糊可除滤子f,因为f(((b→a)→a)→(b∨a))=f(b)= β<α=f(1),所以由定理3.3知f非模糊MV滤子.定理得证.
定理5.4设L是剩余格,f是L的模糊滤子.则f是L的模糊MV滤子当且仅当f既是L的模糊正则滤子又是L的模糊可除滤子.
证必要性:由引理5.1(3)和定理5.3可得.
充分性:设f既是L的模糊正则滤子又是L的模糊可除滤子.任取x,y∈L,令u=x∨y,则
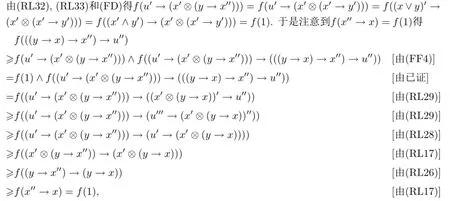
进而再由(RL10)和(FR)得f(((y→x)→x′′)→u)≥f((((y→x)→x′′)→u′′)⊗(u′′→u))≥f(((y→x)→x′′)→u′′)∧f(u′′→u)≥f(1)∧f(1)=f(1).又因为x≤x′′,所以由(RL11)得(y→x)→x≤(y→x)→x′′,进而((y→x)→x′′)→u≤((y→x)→x)→u,故由(FF1)又得f(((y→x)→x)→(x∨y))=f(((y→x)→x)→u)≥f(((y→x)→x′′)→u)≥f(1).再结合(FF3)便得f(((y→x)→x)→(x∨y))=f(1).因此由定理3.3得f是L的模糊MV滤子.定理得证.
定理5.5设L是剩余格.则L的任一模糊MV滤子都是模糊预线性滤子,但反之不真.
证设f是L的模糊MV滤子.任取x,y∈L,因为由(RL15),吸收律,(RL17)和(RL12)可得((x→(x∧y))→(x∧y))→(x∨(x∧y))=((x→y)→(x∧y))→x≤(y→((x→y)→(x∧y)))→(y→x)=((x→y)→(y→(x∧y)))→(y→x)=((x→y)→(y→x))→(y→x),所以由(FF1)和定理3.3得f(((x→y)→(y→x))→(y→x))≥f(((x→(x∧y))→(x∧y))→(x∨(x∧y)))=f(1).故再由(FF4)和定理3.3得f((x→y)∨(y→x))≥f(((x→y)→(y→x))→(y→x))∧f((((x→y)→(y→x))→(y→x))→((x→y)∨(y→x)))≥f(1)∧f(1)=f(1).进而再结合(FF3)便得f((x→y)∨(y→x))=f(1),即(FPL)成立.因此由定理4.1得f是L的模糊预线性滤子.反之,例5.2中所定义的模糊集f为L的模糊预线性滤子,但非模糊MV滤子.定理得证.
下面两个实例揭示了模糊可除滤子和模糊Glivenko滤子与模糊预线性滤子的关系:
例5.5设格L={0,a,b,c,1},L上二元运算→和⊗的定义如下,格L的Hasse图如图1:


图1 L的Hasse图
则(L,≤,∧,∨,⊗,→,0,1)是一个剩余格.在L上定义模糊集f:[0,1]→L使f(0)=f(a)=f(b)= f(c)=β,f(1)=α,其中0≤β<α≤1,可以验证f是L的一个模糊可除滤子,从而为模糊G livenko滤子,但非模糊预线性滤子.这是因为f((a→b)∨(b→a)=f(c)=β<α=f(1).
例5.6设格L=[0,1],L上二元运算→和⊗的定义如下:
则(L,≤,∧,∨,⊗,→,0,1)是剩余格.在L上定义模糊集f:[0,1]→L使f(1)=α,f(x)=β,x∈[0,1),其中0≤β<α≤1,可以验证f是L的一个模糊预线性滤子,但非模糊G livenko滤子,从而非模糊可除滤子.这是因为当取x=0.1时,f(x′′→x)=f(x)=β<α=f(1).
最后,为直观起见,我们将剩余格中各类模糊滤子概念间的关系图示如下:

图2 剩余格中各类特殊模糊滤子间的相互关系
6 结束语
众所周知,在考察逻辑代数的结构时,各类具有不同形式和特殊性质的滤子概念扮演着重要的角色.本文在剩余格这一重要的逻辑代数框架下对模糊滤子理论作了进一步深入研究,引入了剩余格的模糊预线性滤子,模糊可除滤子和模糊G livenko滤子三类全新的模糊滤子概念,获得了它们的若干等价刻画.同时,系统分析了这三类模糊滤子以及剩余格的模糊正关联滤子,模糊Boolean滤子,模糊MV滤子和模糊正则滤子间的相互关系.这些工作不但使剩余格的模糊滤子理论之研究内容得到进一步充实和丰富,概念间的层次关系得到进一步清晰和完善,而且也能为揭示基于剩余格的模糊逻辑系统的结构特征提供理论基础上的支持和保障.
[1]王国俊.非经典数理逻辑与近似推理[M].北京:科学出版社,2005.
[2]W ard M,D ilworth R P.Residuated Lattices[J].Trans Am er M ath Soc,1939,45:335-354.
[3]Pavelka J.On fuzzy logic I,II,III[J].Zeitschr F M ath Logic and Grund lagend M ath,1979,25:45-52,119-134,447-464.
[4]张小红.模糊逻辑及其代数分析[M].北京:科学出版社,2008.
[5]裴道武.基于三角模的模糊逻辑理论及其应用[M].北京:科学出版社,2013.
[6]裴道武.剩余格与正则剩余格的特征[J].数学学报,2002,45(2):271-278.
[7]梁聪,张小红.预线性与对合非结合剩余格[J].模糊系统与数学,2012,26(3):17-23.
[8]朱怡权,曹喜望.关于PFI代数与剩余格[J].数学进展,2006,35(2):223-231.
[9]任兰,张小红.幂等剩余格[J].模糊系统与数学,2011,25(3):21-29.
[10]方进明.剩余格与模糊集[M].北京:科学出版社,2012.
[11]M ichiro K,W ieslaw A D.Filter theory of BL-algebras[J].Soft Com put,2008,12:419-423.
[12]张小红,Jun Y B,Doh M I.关于BL代数的模糊滤子与模糊理想[J].模糊系统与数学,2006,20(3):8-20.
[13]Luo Qingjun.The filter lattices on R0-algebras[J].JMath Res Expos,2009,29(1):169-176.
[14]Liu Lianzhen,Li Kaitai.Boolean filters and positive im p licative filters of residuated lattices[J].In form Sci,2007(177):5725-5738.
[15]Zhu Y iquan,Xu Yang.On filter theory of residuated lattices[J].In form Sci,2010,180: 3614-3632.
[16]Van Gasse B,Deschrijver G,Cornelis C,et al.Filters of residuated lattices and triangle algebras[J].In form Sci,2010,180(16):3006-3020.
[17]Dum itru B,Dana P.Some types of filters on residuated lattices[J].Soft Com put,2014,18: 825-837.
[18]Zhang Xiaohong,Zhou Huijie,M ao Xiaoyan.IM TL(MV)-filters and fuzzy IMTL(MV)-filters of residuated lattices[J].J Intelligent Fuzzy System s,2014,26:589-596.
M R Sub ject C lassification:03G10;06D 35
Fuzzy filters theory of residuated lattices
LIU Chun-hui
(Departm ent of M athem atics and Statistics,Chifeng University,Chifeng 024001,China)
The prob lem of fuzzy filters in residuated lattices is deep ly studied by using the princip le and m ethod of fuzzy sets.Three new notions of fuzzy prelinear,divisib le and G livenko filters are introduced in residuated lattices.Some of their p roperties and characterizations are given. Relations am ong these new fuzzy filters,fuzzy positive im p licative filter,fuzzy Boolean filter,fuzzy MV filter,and fuzzy regu lar filter are discussed systematically.It is p roved that a fuzzy filter is a fuzzy MV filter if and on ly if it is both a fuzzy regu lar filter and a fuzzy d ivisib le filter.
residuated lattice;fuzzy filter;fuzzy prelinear filter;fuzzy divisib le filter;fuzzy G livenko filter
O141.1;O 153.1
A
1000-4424(2016)02-0233-15
2015-05-18
2016-05-04
内蒙古自治区高等学校科学研究项目(NJSY 14283)

