带有类p-Laplacian算子的Kirchhoff型方程的多重解

张申贵，刘　华（西北民族大学数学与计算机科学学院，甘肃兰州730030）

带有类p-Laplacian算子的Kirchhoff型方程的多重解

张申贵，刘华
（西北民族大学数学与计算机科学学院，甘肃兰州730030）

研究一类带有类p-Laplacian算子的K irchhoff型方程.利用对称山路定理，得到了多重解存在的充分条件，推广和改进了已有结果.

Kirchhoff型方程；类p-Lap lacian算子；Dirich let边值问题；临界点

1　引言

考虑D irichlet边值问题

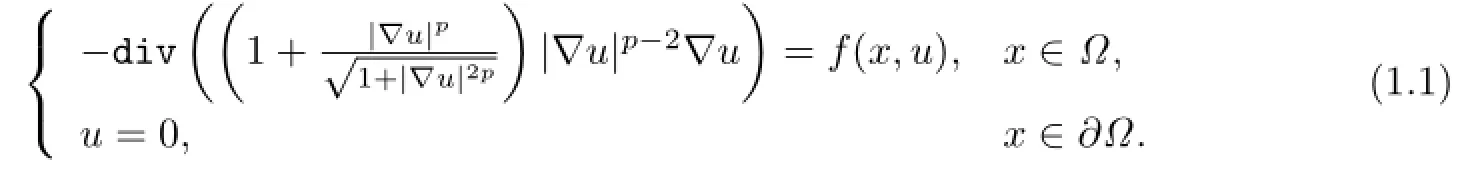
问题（1.1）中带有类p-Lap lacian算子，许多量子力学和流体力学中的数学模型都可以归结为该问题，例如“毛细现象”中广义Cap iliarity方程为

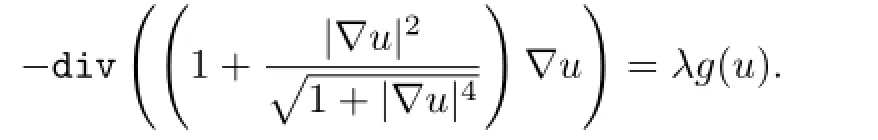
近年来，学者们开始利用临界点理论对带有类p-Lap lacian算子和类p（x）-Lap lacian算子的方程进行了研究，如文［1-9］.当p=2时，P.H.Rabinow itz给出著名的条件：（AR）存R 在µ＞2，L＞0，使得0＜µF（x，u）≤f（x，u）u，对所有x∈Ω和|u|≥L成立，其中F（x，s）=f（x，t）d t.特别地，文献［1］和［2］在条件（AR）成立时，研究了问题（1.1）解的存在性.条件（AR）可以保证非线性项f（x，u）关于变量u在无穷远处是超线性的.（AR）条件被广泛的用于椭圆型偏微分方程边值问题、狄拉克方程、波方程、薛定谔方程和Ham ilton系统解存在性的研究中，但是很多超线性函数并不满足条件（AR）.文［3-5］将条件（AR）推广为更广泛的超线性条件对x∈Ω一致成立，并在此条件下研究了问题（1.1）解的存在性.

在研究古典D’Alembert波方程的弹性弦自由振动的过程中，德国物理学家G.Kirchhoff建立了Kirchhoff方程.高维Kirchhoff模?型可以Z表达为¶

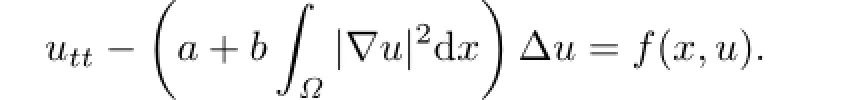
该模型可用于描述生物的种群密度等平均量，其对应的稳态方程为

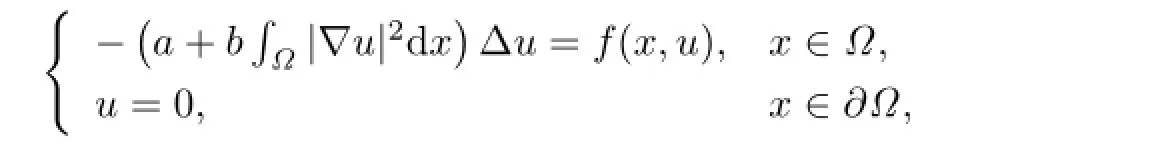
其中a，b为正常数.近年来，变分原理和临界点理论已用于研究K irchhoff稳态方程的可解性.本文中，研究Kirchhoff型方程Dirichlet边值问题

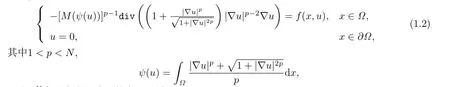
Ω是RN中具有光滑边界的有界区域.

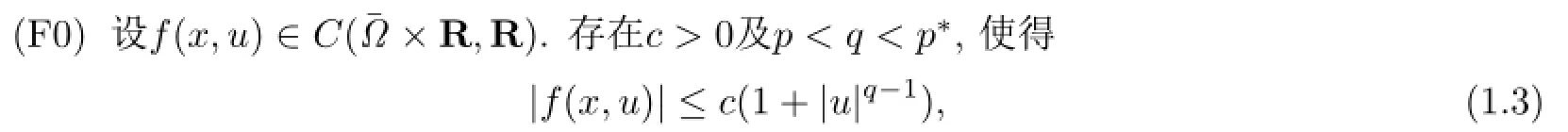
对所有x∈Ω和s∈R成立.其中p∗表示Sobolev临界指数

（M 0）设M（s）∈CR（R+，R+），存在m0＞0，有M（s）≥m0.

易见，问题（1.1）对应于问题（1.2）中M（s）≡1的特殊情形.另外，本文假设非线性项满足局部超线性条件：

（F1）设Ω0为Ω的一个正测度子集，使得一致成立，存在h∈ L1（Ω），有F（x，s）≥-h（x），对所有x∈Ω和s∈R成立.

在局部超线性条件下，将利用临界点理论中的对称山路定理得到问题（1.1）多重解存在性的充分条件.

2　预备知识

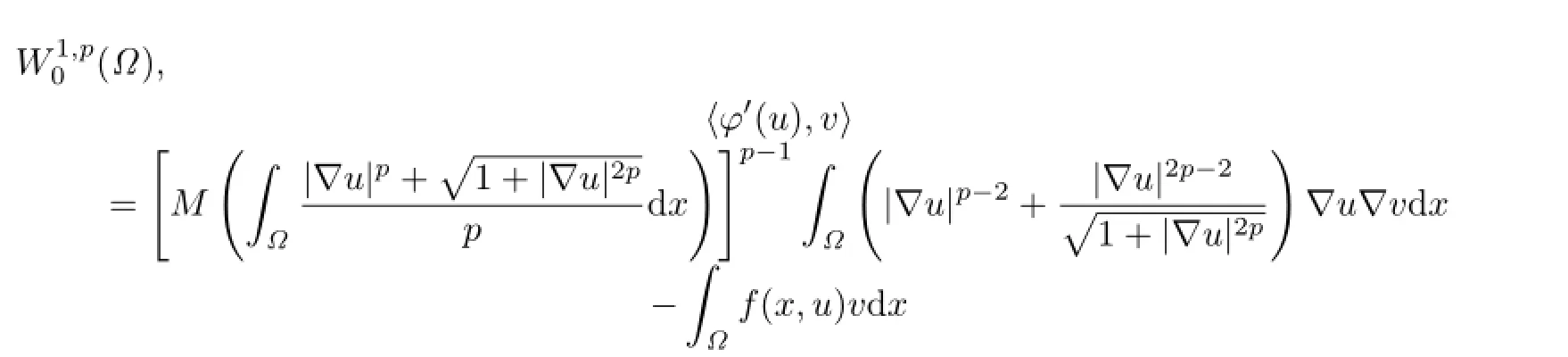
定义2.1［9］设E为Banach空间，若泛函φ∈C1（E，R）满足：对任何｛un｝⊂E，由｛φ（un）｝有有收敛子列，则称泛函φ满足（C）条件.

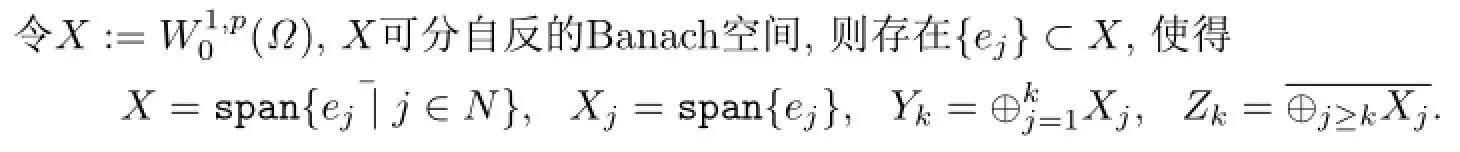
引理2.1［9］（对称山路定理）设E为实Banach空间，E=V⊕X，其中dim V＜+∞.若泛

（i）存在常数ρ，α＞0，使得φ|∂Bρ∩X≥α.

3　主要结果

假设以下条件成立：

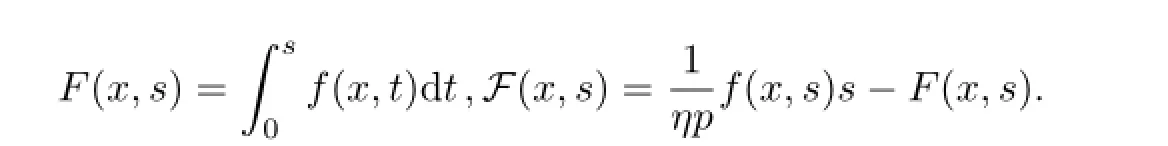
（F2）存在常数L＞0，C1＞0，当|s|≥L时，有F（x，s）≥C1|s|.

（F3）存在常数L＞0，C2＞0，当|s|≥L时，有

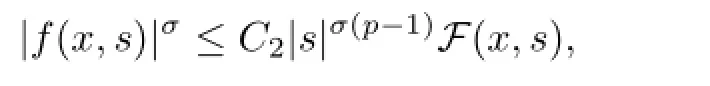
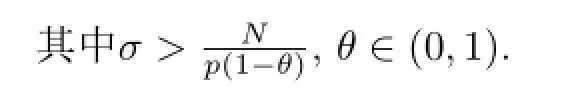
（F4）f（x，-s）=-f（x，s），对所有x∈Ω和s∈R成立.

本文的主要结果如下：

定理3.1设条件（M 0）-（M 1），（F0）-（F4）成立，则对任意的自然数n，问题（1.2）至少有2n个非平凡解.

证利用引理2.1（对称山路定理）证明定理3.1.

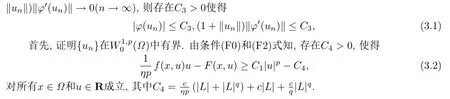
由条件（M 0），（M 1），式（3.2），有

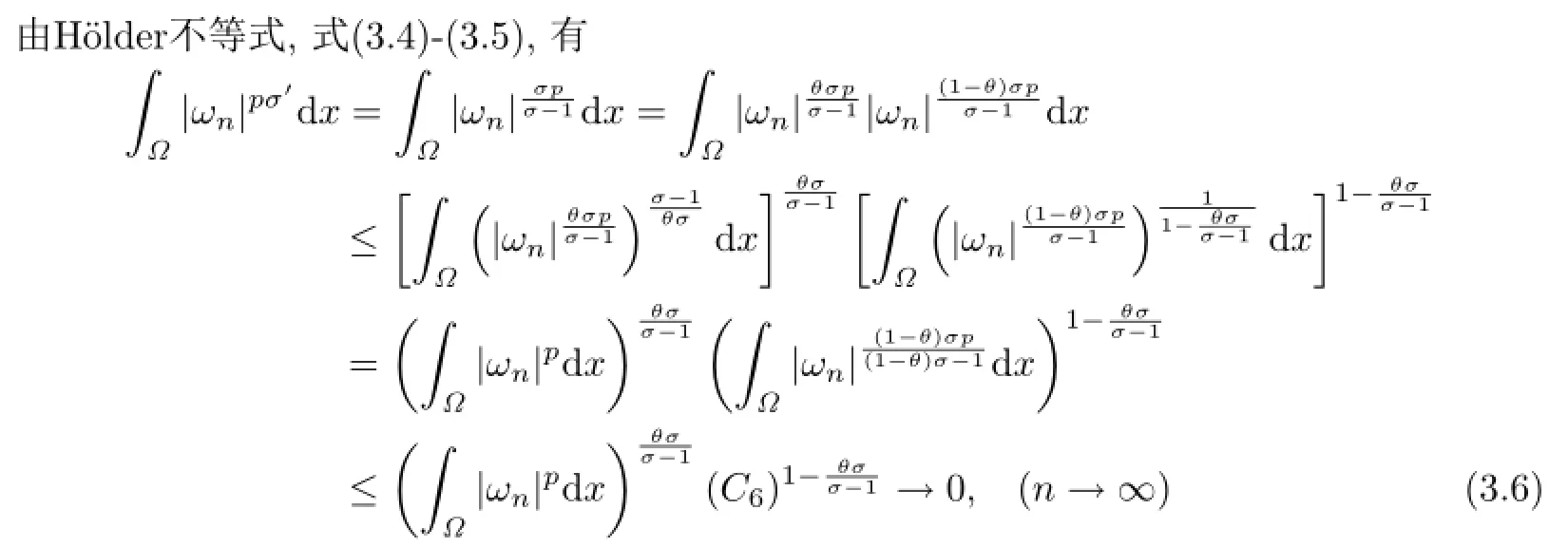
当n充分大时，根据条件（F3）和式（3.1），有

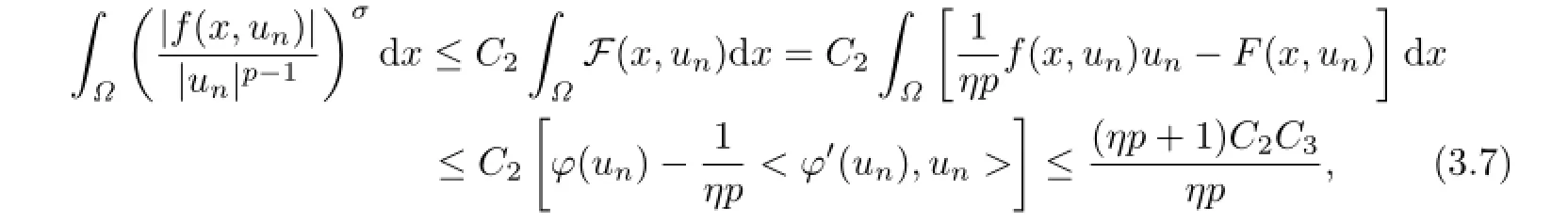
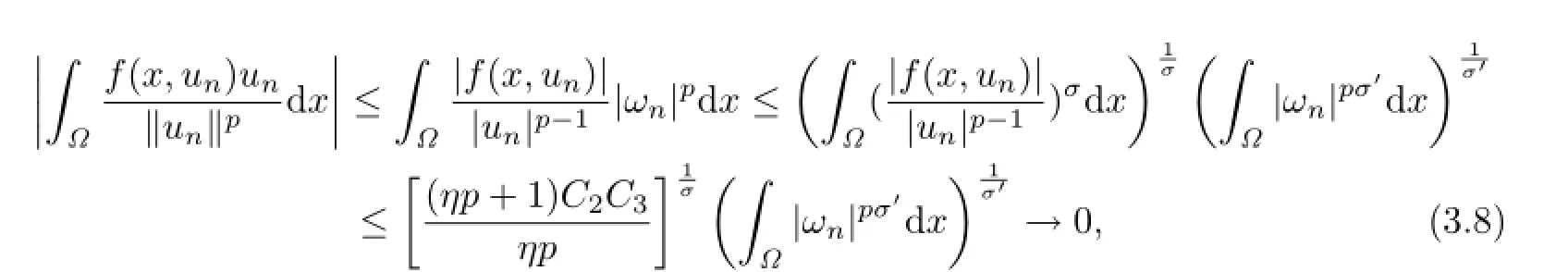
由条件（M 0）及式（2.1），有

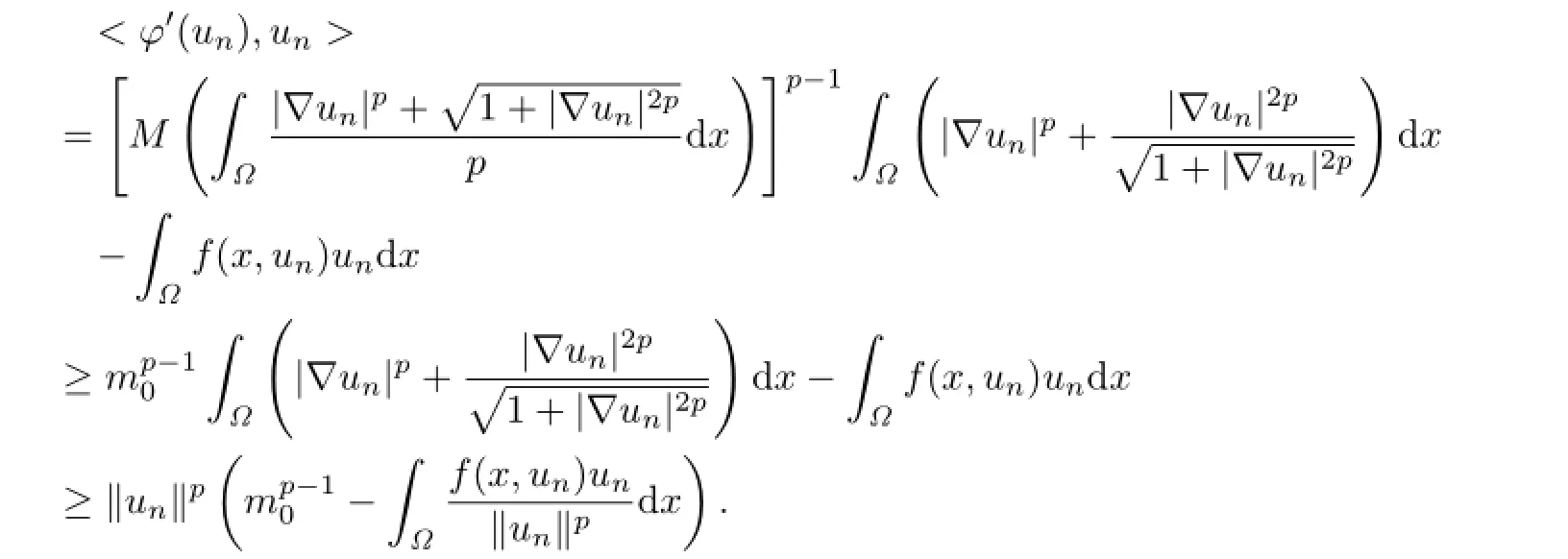
注意到当n→∞时，有‖un‖→∞.由式（3.1），当n充分大时，有

对所有x∈Ω和s∈R成立.

对u∈Zk，利用条件（M 0），（M 1），式（3.10），有

注3.1当M（s）=1，Ω=Ω0，p=2时，则η=1.条件（AR）可以推出条件（F1）-（F3）成立［10］，另一方面，令f（x，u）=a（x）u ln（1+|u|），a（x）＞0，则f满足定理3.1中条件，但不满足条件（AR）.令M（s）=a+bs，p=2，其中a，b为正常数.则M满足（M 0），（M 1）.事实上，令p

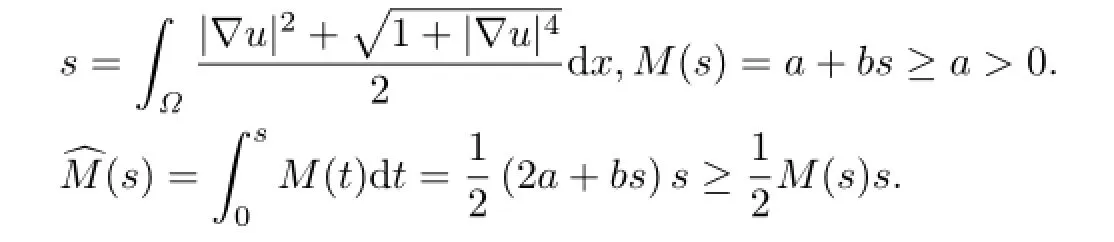
此时，η=2，m0=a，则问题（1.1）可以退化为方程

注3.2文献［2］中研究的问题为

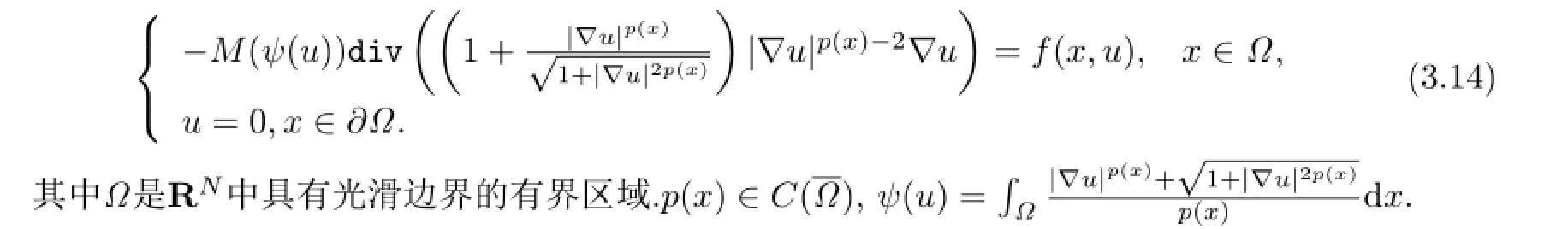
易见，问题（3.14）是更为一般的方程.对比文献［2］中主要结果（Theorem 9），本文中的可解性条件更弱.另外，利用本文中类似讨论，也可以得到问题（3.14）多重解的存在性结果.

［1］Rod rigues M M.Mu ltip licity of solutions on a non linear eigenvalue prob lem for p（x）-Lap lacian-like operators［J］.M editerranean Journal of Mathematics，2012，9（1）:211-223.

［2］Avci M.Ni-Serrin type equations arising from capillarity phenomena w ith non-standard grow th［J］.Boundary Value Prob lem s，2013，55（1）:1-13.

［3］Li Gongbao，Yang Caiyun.The existence of a nontrivial solution to a non linear ellip tic boundary value prob lem of p-Laplacian type w ithout the Ambrosetti-Rabinow itz condition［J］.Non linear Analysis，2010，72（12）:4602-4613.

［4］Ge Bin.On Superlinear p（x）-Lap lacian-like prob lem w ithout Ambrosetti and Rabinow itz condition［J］.Bu lletin of the Korean M athematical Society，2014，51（2）:409-421.

［5］Zhou，Q ingm ei.On the superlinear p roblem s involving p（x）-Lap lacian-like operatorsw ithou t AR-condition［J］.Nonlinear Analysis RealWorld App lications，2015，21:161-169.

［6］陈祖墀，罗涛.类p-Lap lacian方程的特征值问题［J］.数学学报，2003，46（4）:631-638.

［7］Li Zhouxin，Shen Yaotian.Existence of Nontrivial Solutions for p-Lap lacian-Like Equations［J］.Acta M athem aticae A pp licatae Sinica（English Series），2011，27（3）:393-406.

［8］Papageorgiou N S，Papageorgiou E H.Nonlinear boundary value prob lem s involving the p-Lap lacian and p-Lap lacian-like operators［J］.Zeitschrift Analysis und ihre Anwendungen，2005，24（4）:691-707.

［9］W illem M.M inim ax Theorem s［M］.Boston:B irkhauser，1996.

［10］Ding Yanheng，Luan Shixia.M ultiple solutions for a class of nonlinear Schr¨odinger equations［J］.Journal Differential Equations，2004，207:423-457.

M R Su b jec t C lassifica tion:34B 15

M u ltip licity of solu tions for K irchhoff type equation involv ing the p-Lap lacian-like op erator

ZHANG Shen-gui，LIU Hua
（College of M athematics and Com puter Science，Northwest University for Nationalities，Lanzhou 730030，China）

This paper dealsw ith a class of K irchhoff type equation involving the p-Lap lacian-like operator.Base on sysmm etric m ountain pass theorem，som e su fficient cond itions for the ex istence of mu ltiplicity of solutions are obtained，which generalize and im p rove the existing ones.

K irchhoff type equation；p-Lap lacian-like operator；D irichlet boundary value p roblem；critical point

O 175.14

A

1000-4424（2016）02-0153-08

2015-11-27

2016-03-25

国家自然科学基金（31260098）；天元数学基金（11326100）