Sobolev方程一个新的H1-Galerkin混合有限元分析

刁　群，石东洋，张　芳（.平顶山学院数学与统计学院，河南平顶山467000；.郑州大学数学与统计学院，河南郑州45000）

Sobolev方程一个新的H1-Galerkin混合有限元分析

刁群1，石东洋2，张芳2
（1.平顶山学院数学与统计学院，河南平顶山467000；2.郑州大学数学与统计学院，河南郑州450001）

研究了Sobolev方程的H1-Galerkin混合有限元方法.利用不完全双二次元和一阶BDFM元，建立了一个新的混合元模式，通过Bramble-Hilbert引理，证明了单元对应的插值算子具有的高精度结果.进一步，对于半离散和向后欧拉全离散格式，分别导出了原始变量u在H1-模和中间变量p→在H（div）-模意义下的超逼近性质.

Sobolev方程；H1-Galerkin混合有限元方法；Bramble-Hilbert引理；半离散和全离散格式；超逼近

1　引言

考虑如下的Sobolev方程

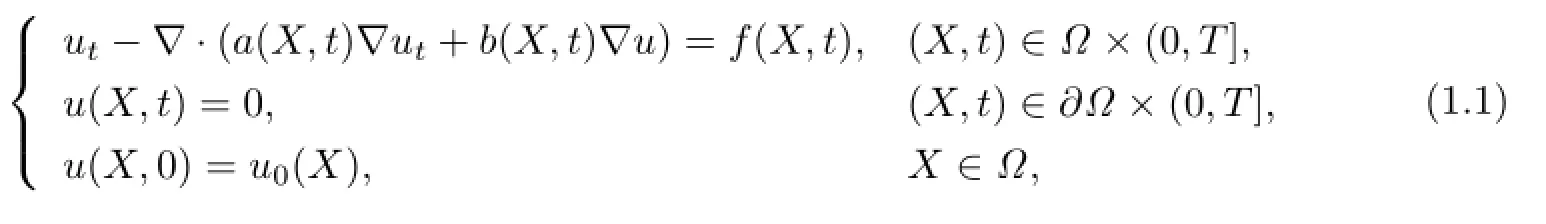
其中Ω为R2上的一个凸多边形区域，∂Ω为其光滑边界，X=（x，y），u0（X）和f（X，t）是已知函数，a（X，t）和b（X，t）为给定的具有有界导数的连续函数，满足

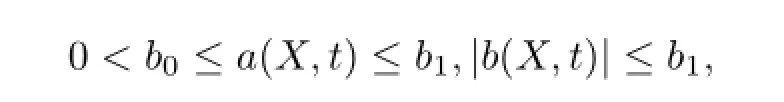
这里b0，b1为常数.

Sobolev方程在流体穿过裂缝岩石的渗透理论，土壤中的湿气迁移问题，不同介质中的热传导问题，黏土的加固理论等许多数学物理问题中有着广泛的应用.关于其数值方法的研究已有很多.对于线性情形，如［1］和［2］分别利用R-T混合元方法和一阶广义差分格式，并借助L2投影或Ritz-Volterra投影，给出了误差分析；［3］和［4］分别研究了各向异性网格下非协调Carey元和W ilson元解的高精度分析，得到了超逼近性质和整体超收敛结果.进一步，借助分裂外推技术，导出了H1-模意义下比通常误差估计提高两阶的收敛速度；［5］提出了时间间断Galerkin有限元方法，得到了最优收敛阶；［6］和［7］分别建立了非协调混合元）和协调混合元（Q11+Q01×Q10）格式，得到了半离散和全离散格式下的超逼近性质和整体超收敛结果.对于非线性情形，如［8］给出了非协调元方法的半离散和向后欧拉全离散格式，证明了最优收敛阶，超逼近和整体超收敛结果；［9］讨论了类W ilson元的超收敛分析及外推；［10］研究了经济型差分-流线扩散非协调有限元方法，分别给出了Euler-EFDSD和Crank-Nicolson-EFDSD格式的最优误差估计.

众所周知，混合有限元方法是求偏微分方程数值解的有效方法之一，但它需要所涉及的两个有限元逼近空间满足所谓的inf-sup条件或B-B相容性条件，这通常不是一件很容易的事.为了克服这一要求，降低空间匹配的难度，Pani在［11］中提出了H1-Galerkin混合有限元方法.后来，被广泛应用于很多有实际背景的问题［12-16］.但就作者所知，该方法对Sobolev方程的应用，目前还仅局限于收敛性的研究，并且大多数需要借助于不同形式的投影算子进行误差分析［17-20］.

本文的主要目的是利用不完全双二次元Q-2和一阶BDFM元，对Sobolev方程构造一个新的H1-Galerkin混合元模式.首先，通过Bramb le-Hilbert引理，证明了单元对应的插值算子具有的新的高精度结果.其次，在不需要借助传统有限元分析中必不可少的投影算子的前提下，对于半离散和全离散格式，分别导出了原始变量u在H1-模和中间变量→p在H（div）-模意义下的超逼近性质.且对全离散格式来说，该性质还是无条件的，即不需要网格比就能得到.

2　混合元的构造及性质

设Ω是一个矩形区域，其边界∂Ω分别平行于x轴和y轴，Th是Ω的矩形单元剖分族，满足正则性假设.对e∈Th，设其四个顶点分别为a1（xe-he，ye-ke），a2（xe+he，ye-ke），a3（xe+ he，ye+ke），a4（xe-he，ye+ke）.四条边分别为记平面上的参考单元为四个顶点为四条边.

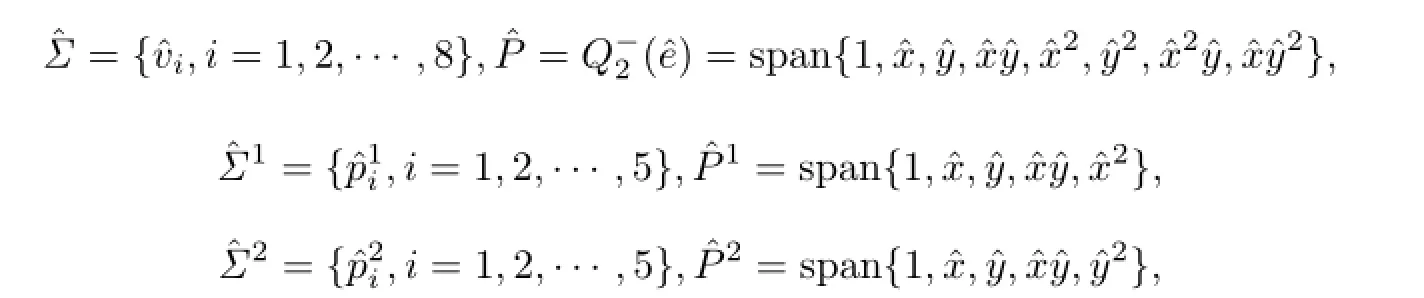
其中

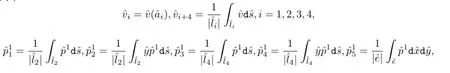
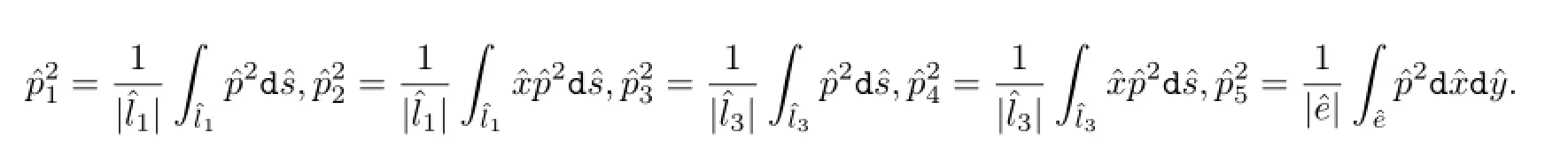
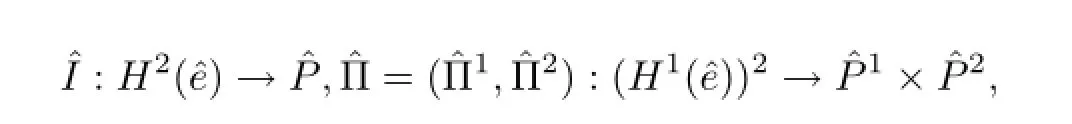
满足

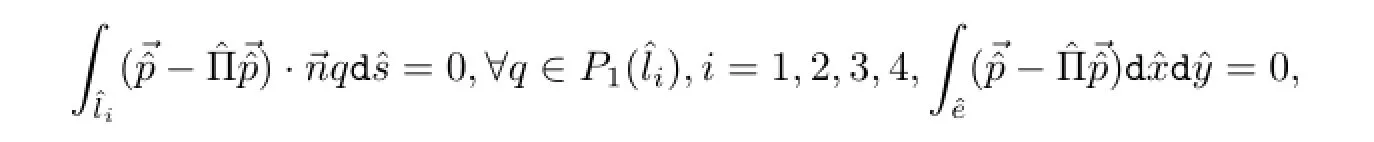
可以验证，以上定义的插值算子是适定的，插值函数表达式分别为

其中

定义可逆仿射变换Fe

那么相应的有限元空间以及所诱导的插值算子分别为

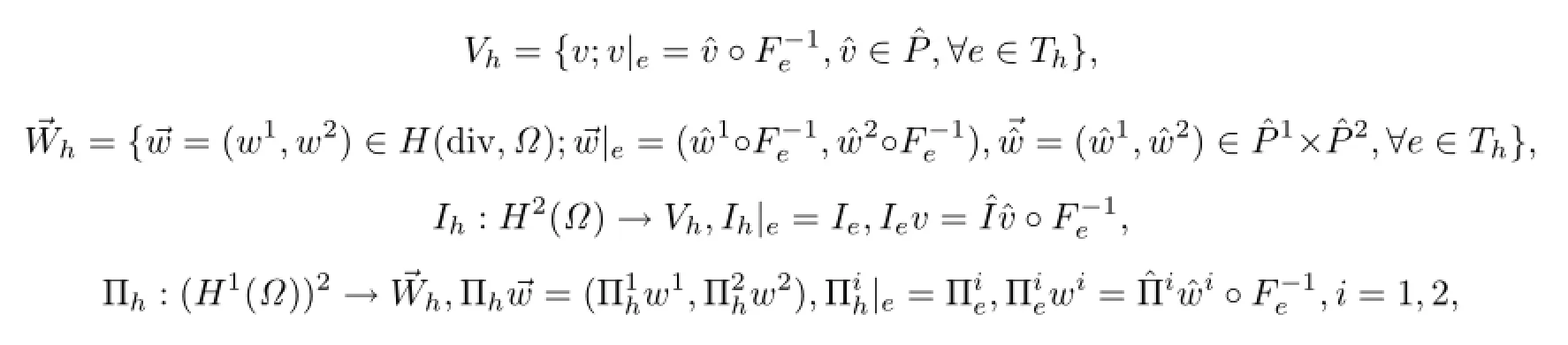
引理2.1［21］若u∈H4（Ω），则有

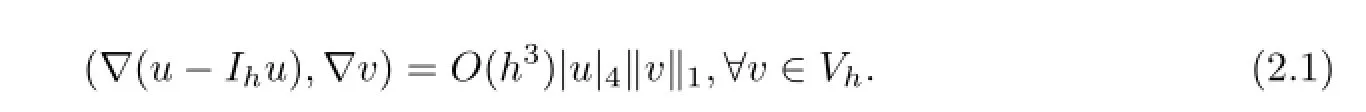
引理2.2若→p=（p1，p2）∈（H3（Ω））2，则有

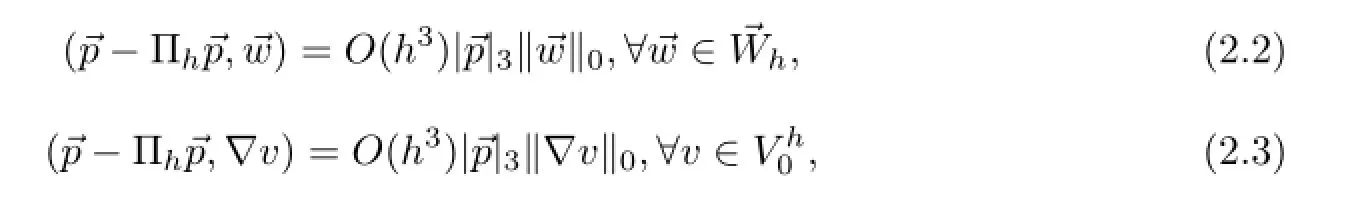
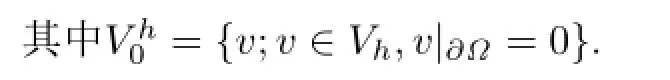
证［22］中已给出（2.2）式的证明.下面证明（2.3）式.

由Sobolev嵌入定理和逆不等式，有

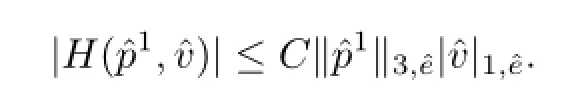
这里P2）为单元eˆ上的二次多项式空间.由Bramble-Hilbert引理，知

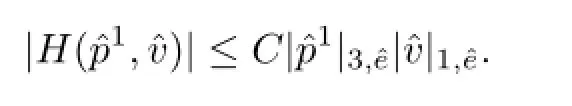
于是

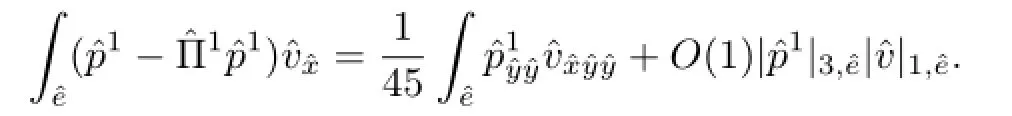
通过仿射变换，可得

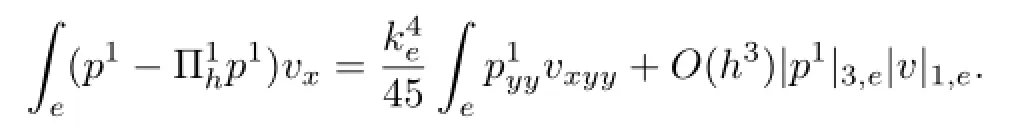
注意到利用格林公式，有

喉口面积明确之后，由经验公式可知文丘里管喷嘴长度L1、混合段长度Lt和扩压器长度L2。为让文丘里管收缩角度及扩张角度在合适锥角范围以内，由试验台架的位置布置，分别计算得到文丘里管收缩段、喉口混合段和扩压段长度。具体结构参数见表1,实物见图3。

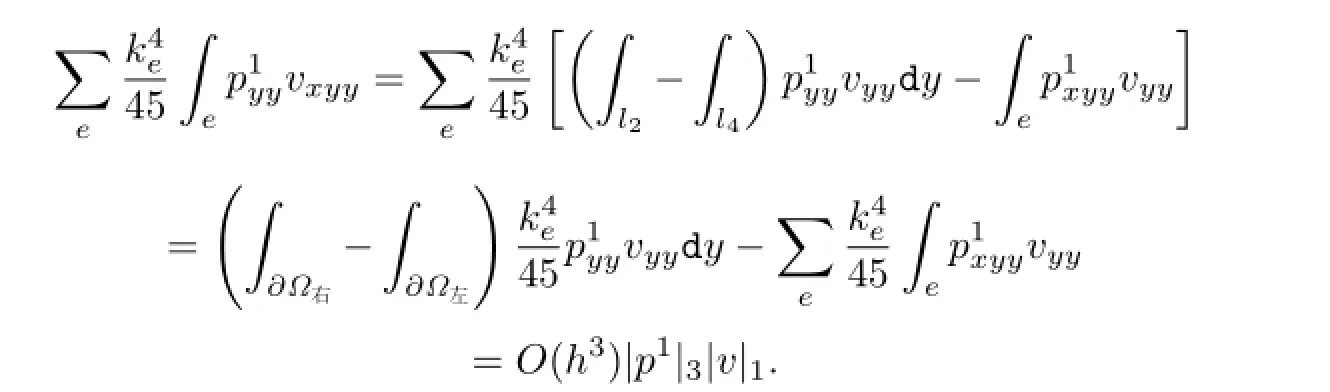
综合以上两式，即得（2.3）式.

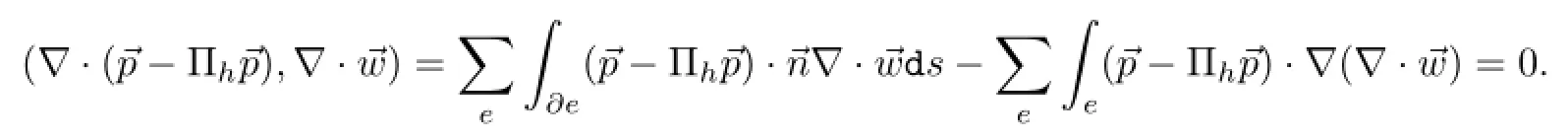
3　半离散格式下的超逼近分析

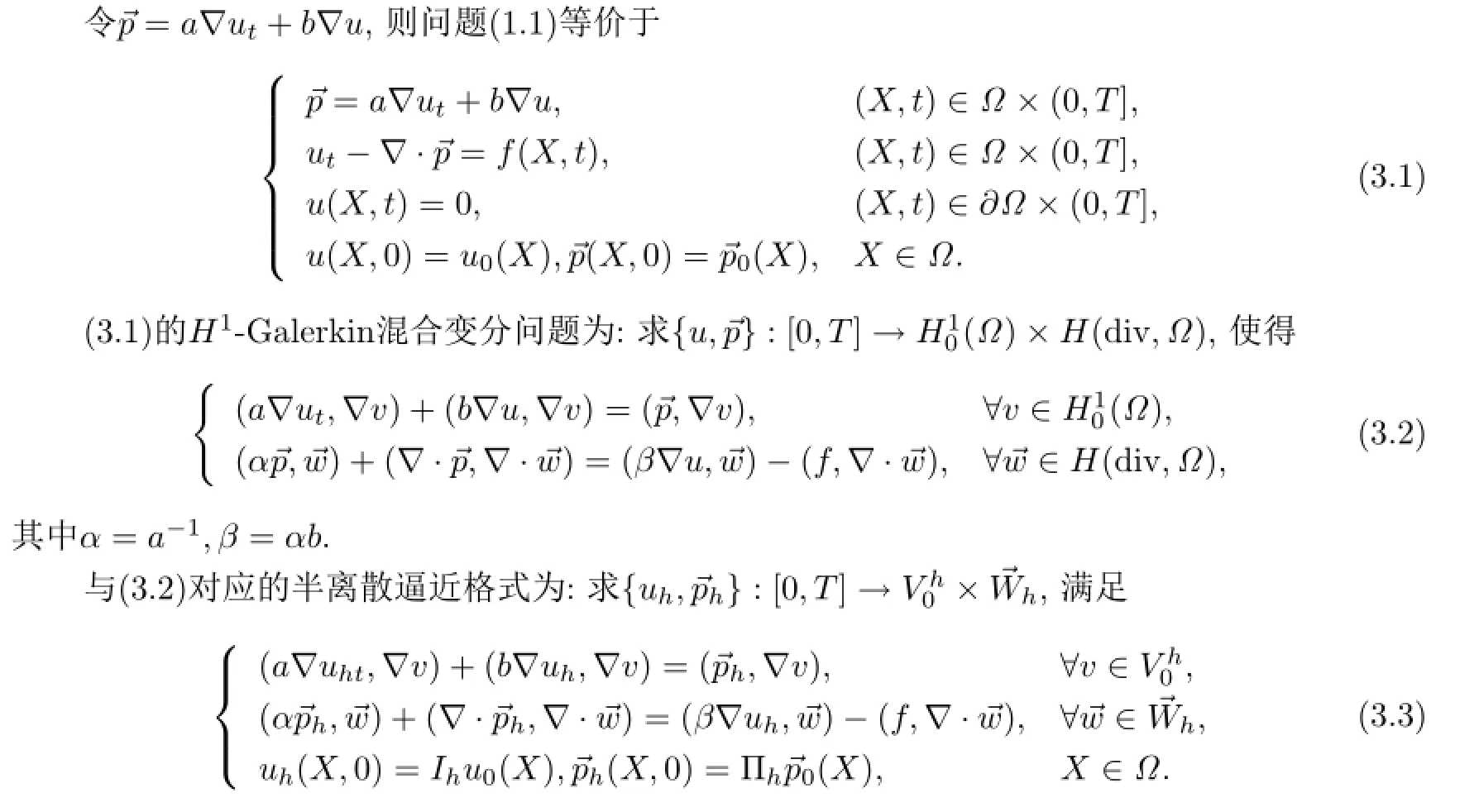
类似于［17］可以证明问题（3.3）存在唯一解.

一方面，在（3.6）的第一式中令v=ξ，可得

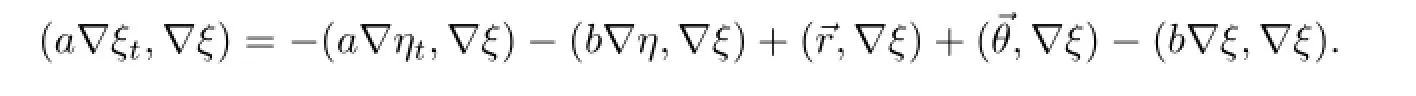
即

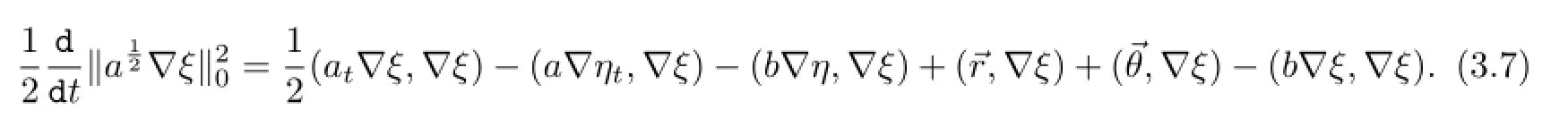
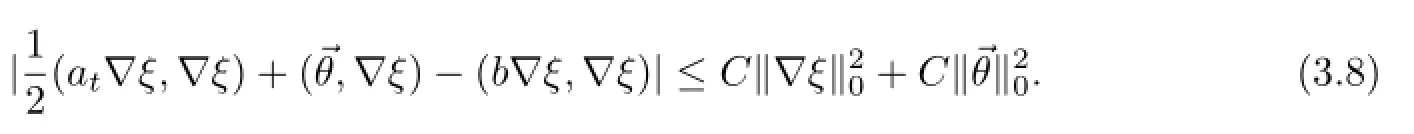
对任意的φ∈W1，∞（Ω），定义其在单元e上的平均值则有

利用平均值技巧、插值理论和引理2.1，可得

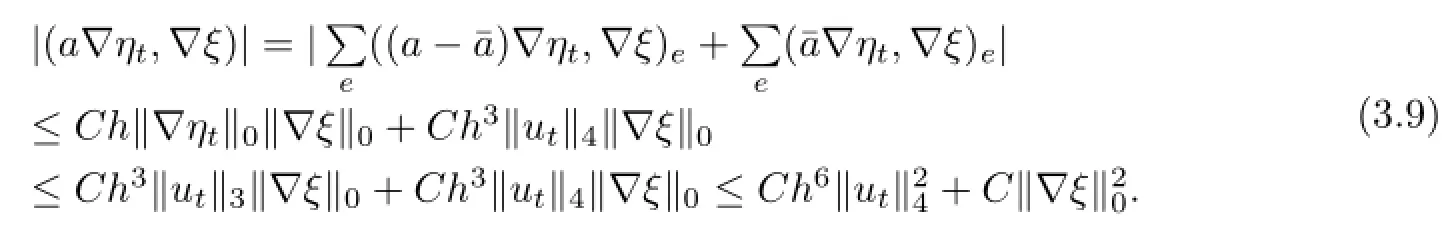
类似的，有

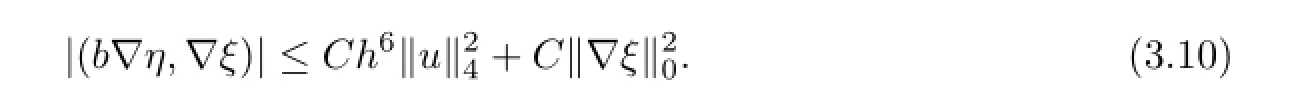
再由引理2.2，可得

把（3.8）-（3.11）与（3.7）结合，有

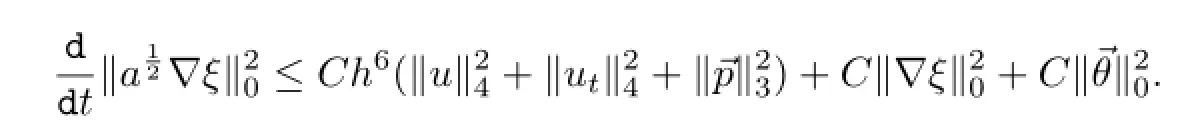
对上式两边从0到t积分，由∇ξ（X，0）=0及G ronwall引理，得

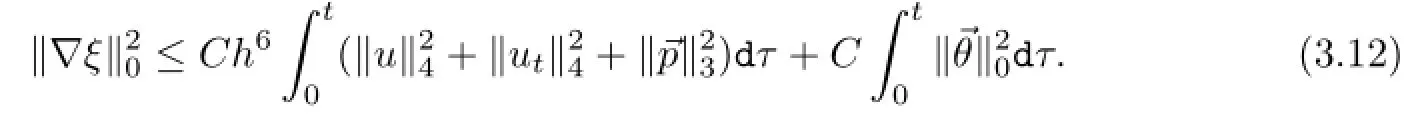
另一方面，在（3.6）的第二式中令→w=→θ，有

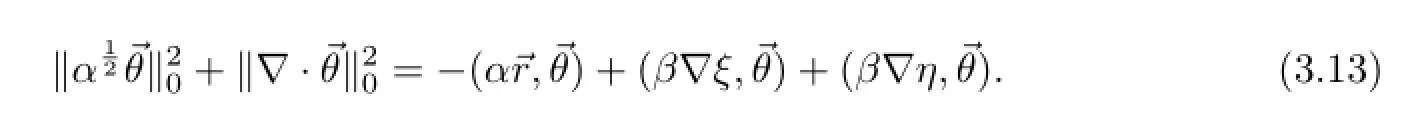
利用平均值技巧和引理2.2，可得

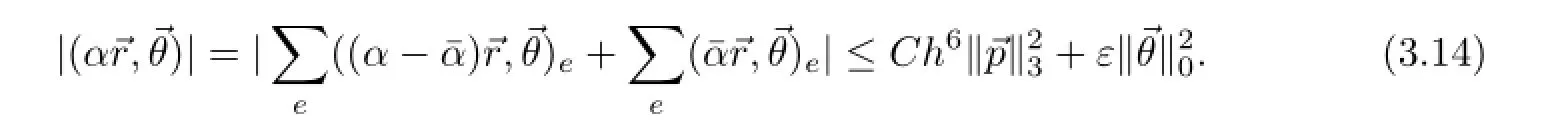
根据函数β的有界性，有

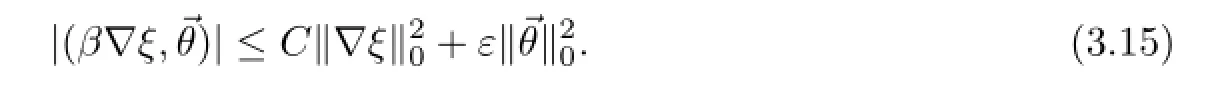
由于u|∂Ω=0，从而可得η|∂Ω=0，所以由格林公式，知

把（3.14）-（3.16）与（3.13）结合，并取适当小的ε，有

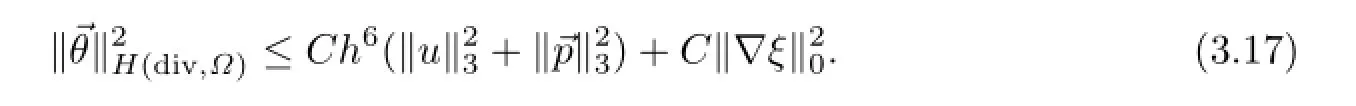
将（3.17）代入到（3.12），由Gronwall引理可得（3.4）.再把（3.4）代入到（3.17）即得（3.5）.证毕.

注2定理3.1证明过程中关键的地方在于对（β∇η，→θ）的估计，这里需要应用单元特有的插值条件，才能由格林公式得到（3.16）的结果，从而得出本定理的结论.

4　全离散格式下的超逼近分析

设0=t0＜t1＜···＜tN=T为［0，T］的等距剖分对任意的光滑函数

类似于［17］可以证明问题（4.1）存在唯一解.

在（3.2）中令t=tn，可得

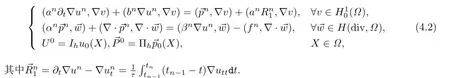
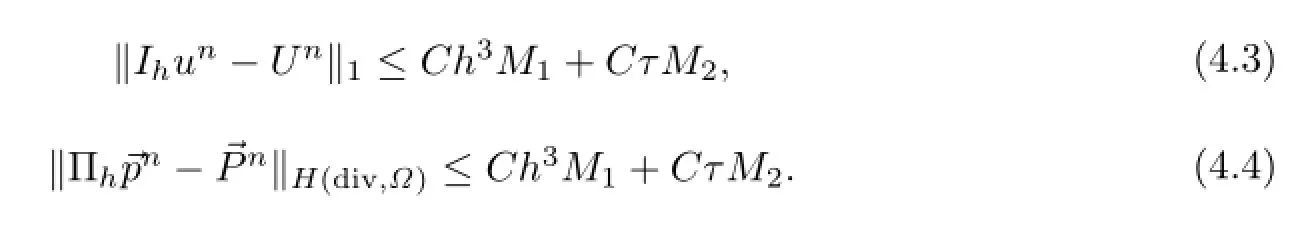
其中

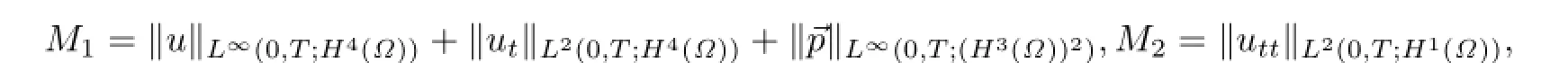
这里

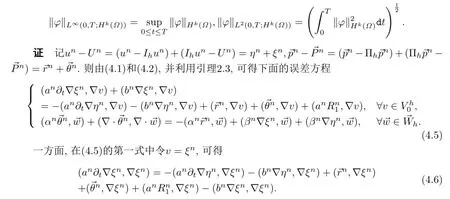
由于

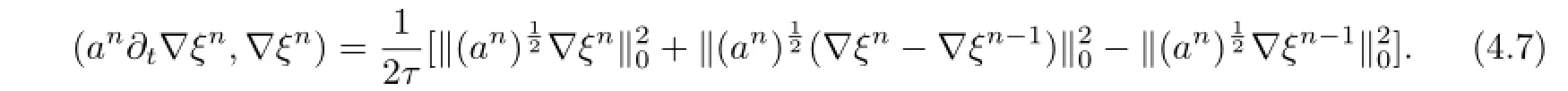
而（4.6）的右端项可依次估计为

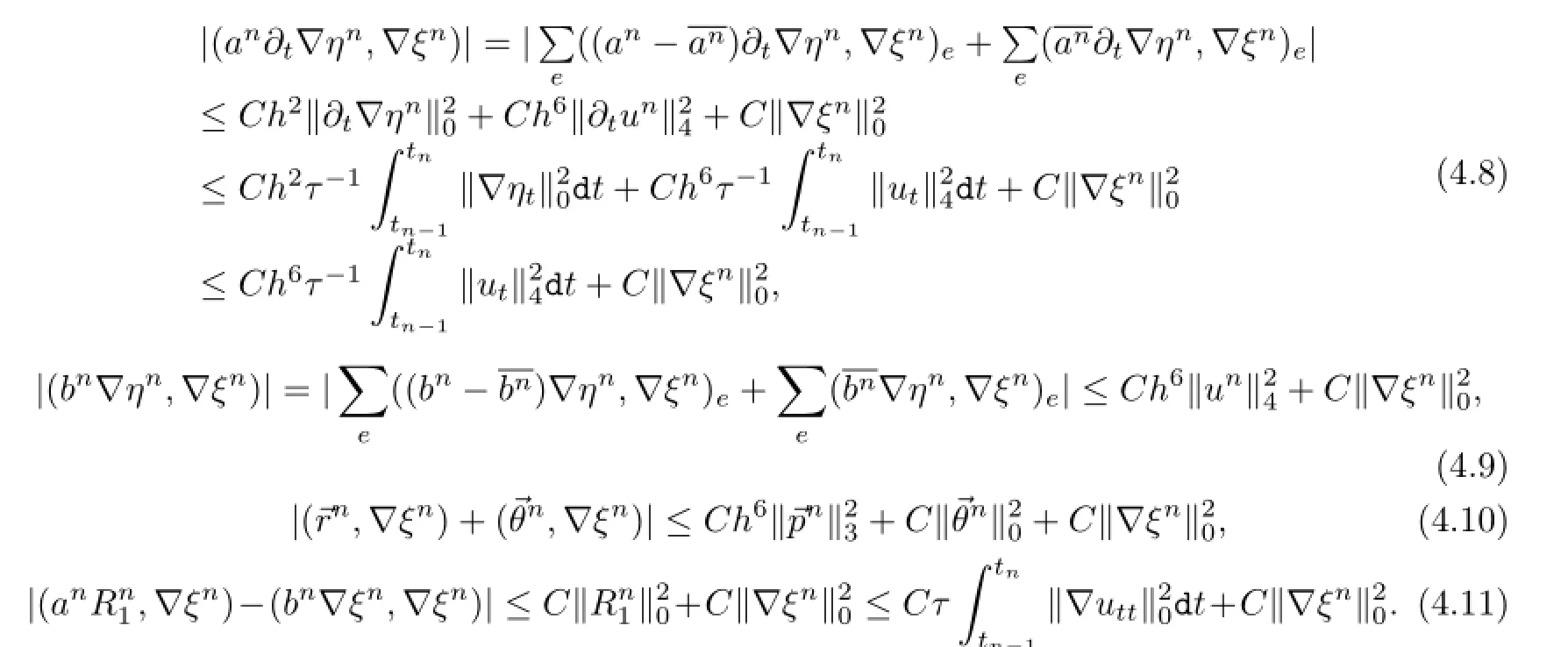
把（4.7）-（4.11）代入到（4.6），可得

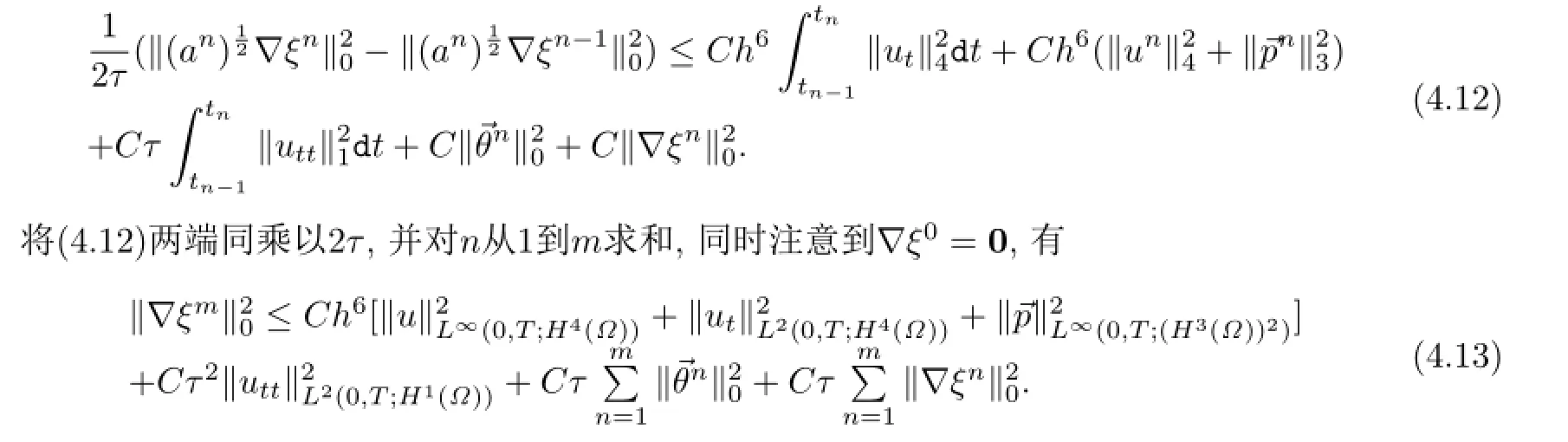
在（4.13）中取充分小的τ，使得1-Cτ＞0，由离散的Gronwall引理，可得

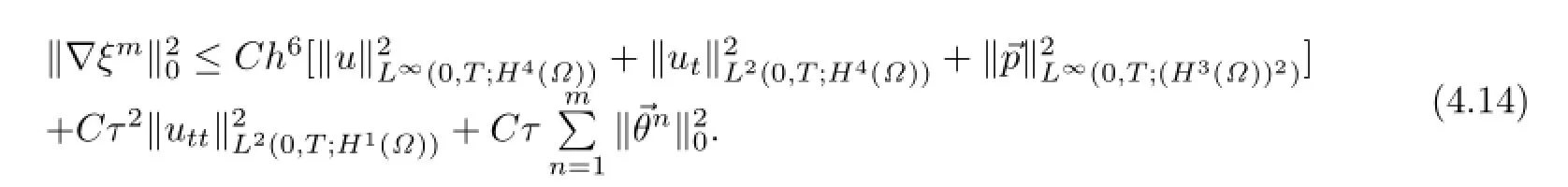
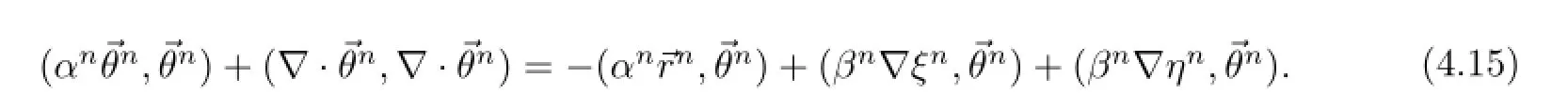
（4.15）的右端项可依次估计为

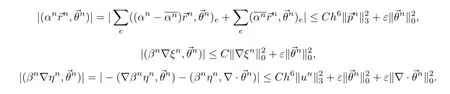
把以上估计代入（4.15），并取适当小的ε，有

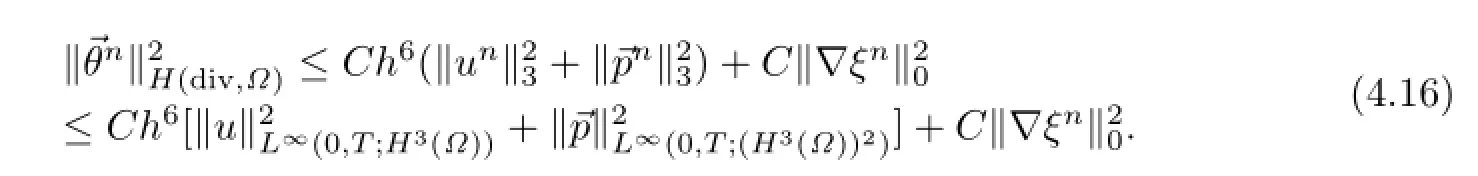
结合（4.14）与（4.16），由离散的G ronwall引理，即得定理结论.

［1］Jiang Ziwen，Chen Huanzhen.Error estimates ofm ixed finite elementmethods for Sobolev equation［J］.Northeast M ath J，2001，17（3）:301-314.

［2］曹艳华.二维线性Sobolev方程广义差分法［J］.计算数学，2005，27（3）:243-256.

［3］石东洋，郝晓斌.Sobolev型方程各向异性Carey解的高精度分析［J］.工程数学学报，2009，26（6）: 1021-1026.

［4］石东洋，任金城，郝晓斌.Sobolev型方程各向异性网格下W ilson元的高精度分析［J］.高等学校计算数学学报，2009，31（2）:169-180.

［5］何斯日古楞，李宏.Sobolev方程的时间间断Galerkin有限元方法［J］.高校应用数学学报，2011，26（4）:467-473.

［6］Shi Dongyang，Zhang Yadong.High accuracy analysis of a new noncon form ingm ixed finite element scheme for Sobolev equations［J］.App lM ath Com put，2011，218（7）:3176-3186.

［7］史艳华，石东洋.Sobolev方程新混合元方法的高精度分析［J］.系统科学与数学，2014，34（4）: 452-463.

［8］Shi Dongyang，Wang Haihong，Du Yuepeng.An anisotropic noncon form ing finite element m ethod for app roxim ating a class of non linear Sobolev equations［J］.J Com pu t M ath，2009，27（2-3）:299-314.

［9］ShiDongyang，Wang Fen ling，Zhao Yanm in.Superconvergenceanalysisand ex trapolation of quasi-W ilson nonconform ing finite elementmethod for non linear Sobolev equations［J］.Acta Math Appl Sin（English Ser），2013，29（2）:403-414.

［10］石东洋，王海红.非线性Sobolev方程的经济型差分-流线扩散非协调有限元法［J］.数学物理学报，2013，33A（6）:1148-1161.

［11］Pani A K.An H1-Galerkin m ixed finite element methods for parabolic partial differential equations［J］.SIAM J Numer Anal，1998，35（2）:721-727.

［12］王瑞文.双曲型积分微分方程H1-Galerkin混合元法的误差估计［J］.计算数学，2006，28（1）: 19-30.

［13］刘洋，李宏，何斯日古楞.伪双曲型积分-微分方程H1-Galerkin混合元法误差估计［J］.高等学校计算数学学报，2010，32（1）:1-20.

［14］陈红斌，刘晓奇，徐大.粘弹性双曲型方程的H1-Galerkin混合有限元方法［J］.高等学校计算数学学报，2011，33（3）:279-288.

［15］石东洋，唐启立，董晓靖.强阻尼波动方程的H1-Galerkin混合有限元超收敛分析［J］.计算数学，2012，34（3）:317-328.

［16］石东洋，史艳华，王芬玲.四阶抛物方程H1-Galerkin混合有限元方法的超逼近及最优误差估计［J］.计算数学，2014，36（4）:363-380.

［17］郭玲，陈焕贞.Sobolev方程的H1-Galerkin混合有限元方法［J］.系统科学与数学，2006，26（3）: 301-314.

［18］Shi Dongyang，Wang Haihong.Nonconform ing H1-Galerkin m ixed FEM for Sobolev equ tions on anisotropic m eshes［J］.A cta M ath A pp l Sin（English Ser），2009，25（2）:335-344.

［19］李宏，季兆义，刘洋等.Sobolev方程的一类新型H1-Galerkin混合元法［J］.高等学校计算数学学报，2013，35（3）:206-221.

［20］王金凤，刘洋，李宏等.Sobolev方程的基于H1-Galerkin混合方法的新分裂格式［J］.高等学校计算数学学报，2014，36（1）:32-48.

［21］郝晓斌.非协调有限元的构造及其应用［D］.郑州:郑州大学博士学位论文，2008.

［22］林群，严宁宁.高效有限元构造与分析［M］.保定:河北大学出版社，1996.

M R Sub ject C lassification:65N 15；65N30

A new H1-Galerk in m ixed finite elem ent analysis for Sobo lev equation

DIAO Qun1，SHIDong-yang2，ZHANG Fang2
（1.School of M ath.Statis.，Pingdingshan Univ.，Pingdingshan 467000，China；2.School of M ath.Statis.，Zhengzhou Univ.，Zhengzhou 450001，China）

In this paper，H1-Galerkinm ixed finite elementmethod for Sobolev equation is studied.A new m ixed finite elem ent pattern is constructed using incom p lete biquad ratic elem ent Q-2and first order BDFM element.Through Bramble-Hilbert lemma，high p recision resu lts of interpolation operators correspond ing to unit are p roved.Further，the superclose p roperties for the prim itive variables u in H1-norm and the intermediate variable→p in H（div）-norm are obtained respectively in sem i-discrete and the backw ard Eu ler fu lly d iscrete schem es.

Sobolev equation；H1-Galerkinm ixed finiteelementmethod；Bramble-Hilbert lemma；sem i-discrete and fu lly discrete schemes；superclose

O 242.21

A

1000-4424（2016）02-0215-10

2015-04-10

2016-04-25

国家自然科学基金（11271340）；河南省科技计划项目（162300410082）