Majorana zero modes induced by skyrmion lattice

Dong-Yang Jing(靖东洋), Huan-Yu Wang(王寰宇), Wen-Xiang Guo(郭文祥), and Wu-Ming Liu(刘伍明),3,†

1Beijing National Laboratory for Condensed Matter Physics,and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

3Songshan Lake Materials Laboratory,Dongguan 523808,China

4TIPC-LNE Joint Laboratory on Cryogenic Metrology Science and Technology,Technical Institute of Physics and Chemistry,Chinese Academy of Sciences,Beijing 100190,China

5CAS Key Laboratory of Cryogenics,Technical Institute of Physics and Chemistry,Chinese Academy of Sciences,Beijing 100190,China

Keywords: topological superconductor,Majorana zero mode,spin–orbit coupling

1. Introduction

Majorana fermions are localized edge modes in modern condensed matter physics, rather than a hypothetical basic particle, which is a real solution of the Dirac equation,in high energy physics.[1,2]More precisely, in second quantized formulation, the creation and annihilation operators for Majorana fermions coincide with each other, and they are non-abelian anyons.[3,4]In recent years, more and more research are focused on the realization of Majorana zero modes as they have a wide variety of potential applications, such as fault tolerent quantum computation, quantum information and communication.[5–10]Majorana zero modes have been observed in both 1D and 2D s-wave superconductor systems with strong spin–orbit interaction or cold atomic systems. One of the mostly studied model supporting Majorana zero modes was proposed by Kitaev, which has brought physicists to intuitively understand these attractive modes.

Skyrmion lattice is a great topic in both condensed matter physics and cold atomic physics.[11–17]Especially in Bose–Einstein condensates (BECs), skyrmion is a topological soliton. There are a lot of kinds of skyrmions in BECs and a lot of theoretical and numerical results are obtained. In another perspective, skyrmion is a spin (or psuedo-spin, magnetic) configuration, with which the spin exchange would lead to some topological non-trivial phases. There are also some experimental progress in observing and manipulating skyrmions in condensed matter physics.[18]

Though there are lots of theoretical results about the constant spin–orbit coupling s-wave superconductor system,[19–22]there is little work about the spin-exchange effect between s-wave superconductor and skyrmions,which effectively induces non-constant spin–orbit coupling and leads to a rich topological phase diagram. Experimentally, achieving the topological superconductor through proximity effect decouples the realization of spin–orbit coupling and s-wave superconductor,and it takes the advantage of the fact that there are lots of spin configurations, including skyrmions, which have been achieved in cold atomic physics. The only step to go is to implement the spin-exchange effect between these two systems. Compared with the Raman assisted hopping, which induces the constant spin–orbit coupling, this spin-exchange effect is accompanied by a more fruitful phenomenon. In contrast to directly realizing the non-constant spin–orbit coupling in an s-wave superconductor by a more complicated setup,the effect of this spin exchange is more practical and can serve as another important platform of realization of topological superconductor. Our work makes a foundation of this possibility and gives a good intuition about this novel spin-exchange effect.

Our paper is organized as follows. In Section 2, we present the lattice model describing the s-wave superconductor in proximity to magnetic skyrmions which effectively introduces a Rashba spin–orbit interaction. Also, we analyze the symmetry of the system, and obtain the formulation of topological invariants in the framework of AZ 10-fold classification. In Section 3, we show the numerical results, including topological phase diagrams, spectrum structures, and density distribution of Majorana zero modes(MZMs).Finally,we give a conclusion.

2. The model and calculation

We start with a one-dimensional s-wave superconductor system in proximity to magnetic skyrmions, which is equivalent to a Rashba spin–orbit coupling superconductor. It is described by the following Hamiltonian:

wherecx,αannihilates an electron at lattice sitexwith spinα,andσ=(σ(1),σ(2),σ(3))is the vector of spin Pauli matrices. We consider spatial spin configurationSxwith radiusR,as depicted in Fig.1(R=6),and exchange coupling between skyrmions and electron spinsJ,hopping amplitude-txx′=-tbetween nearest-neighbor sites only.Δis the s-wave pairing amplitude,Bxis the magnitude of transverse magnetic field.

We also assume that the radius of skyrmion is commensurate with the length of system. The spin configuration of skyrmionSxis

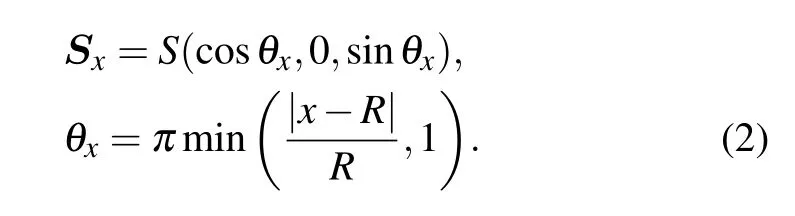
In the following calculations,we set the hopping amplitude between nearest neighbor to be the unit of energy,i.e.,t=1. To illustrate that such an exchange coupling can induce a Rashba spin–orbit interaction,we make a local unitary transformation ˆUxthat rotates the local spinSxof skyrmion to thexdirection:

where the representation of transformation could be

It is an unitary operator. The spinful annihilation operators of fermions of latticexunder this transformation are (dx↑,dx↓),satisfying

The Hamiltonian in rotating frame is given by

whereTxx′ =. ParameterJSdenotes the product of the spin exchange amplitude and the spin of skyrmion. By Eq. (4), we could go a step further in the hopping terms in Eq. (6). By defining the angle difference between nearest neighbors asdθx=θx′/2-θx/2, we could get a formulation ofTxx′:

So far, we have shown that an s-wave superconductor in proximity to magnetic skyrmions is equivalent to a Rahsba spin–orbit coupling s-wave superconductor system. The spin–orbit coupling strength is negatively correlated with skyrmion radius. The spin exchange coupling would induce an effective transverse magnetic field. Later, we will show the numerical results of the topological transition induced by such a spin–orbit coupling.

As the transverse magnetic field and skyrmions both would break the time reversal symmetry, the system belongs to class D according to AZ ten fold way topological classification. The topological phases are characterized byZ2topological invariants.[23]

As we assume that the radius of skymion is commensurate to the lattice constant,we can make a Fourier transformation to represent Eq. (1) in Brillioun zone. The unit cell of the system contains 2Rsites. The Hamiltonian in the Brillioun zone reads

whereck=(c1k↑,c1k↓,...,c2Rk↑,c2Rk↓). The first subscript denotes the sublattice site. The matrix form of the hopping can be written as

3. Topological invariants and phase diagram

We could obtain the topological phase diagram by evaluating the topological invariant for each phase. In this 1D class superconductor system, the topological properties of each phase is characterized by winding numberWdefined by Chern–Simons(CS)integralCS[A]as[24]

and it is quantized to be±1. From the particle hole symmetry of the system,we could obtain the relation between the Berry connections defined by negative and positive energy bands:

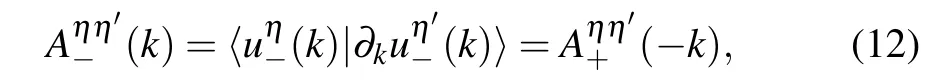
in which the band indicesηandη′are over negative energy bands. Thus,the 1D CS integral can be written as

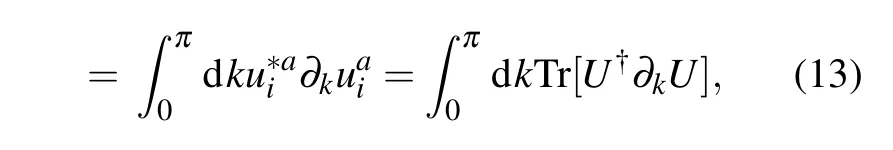
where the band indexatakes over all energy bands. In the last equality, we set the matrix elements as(k)=(k). The topological non-trivial phase is accompanied with a negative winding number.

The topological phases and corresponding topological invariants of the system described by Eq. (1) are depicted in Fig.2(a),and we set the parameters asBx=0.5 andΔ=0.3.

Figures 2(a1),2(a2),and 2(a3)present the result with the radii of skyrmion lattice beingR=7,R=9, andR=12, respectively. The vertical axis represents the parameterμ, and the horizontal axis denotes the parameterJS. The blue lines in these figures are topological phase boundaries. We also mark the region with winding numberW=-1, i.e., the topological non-trivial regions. We could see that with the increasing radius,the phase diagram would be more complicated.

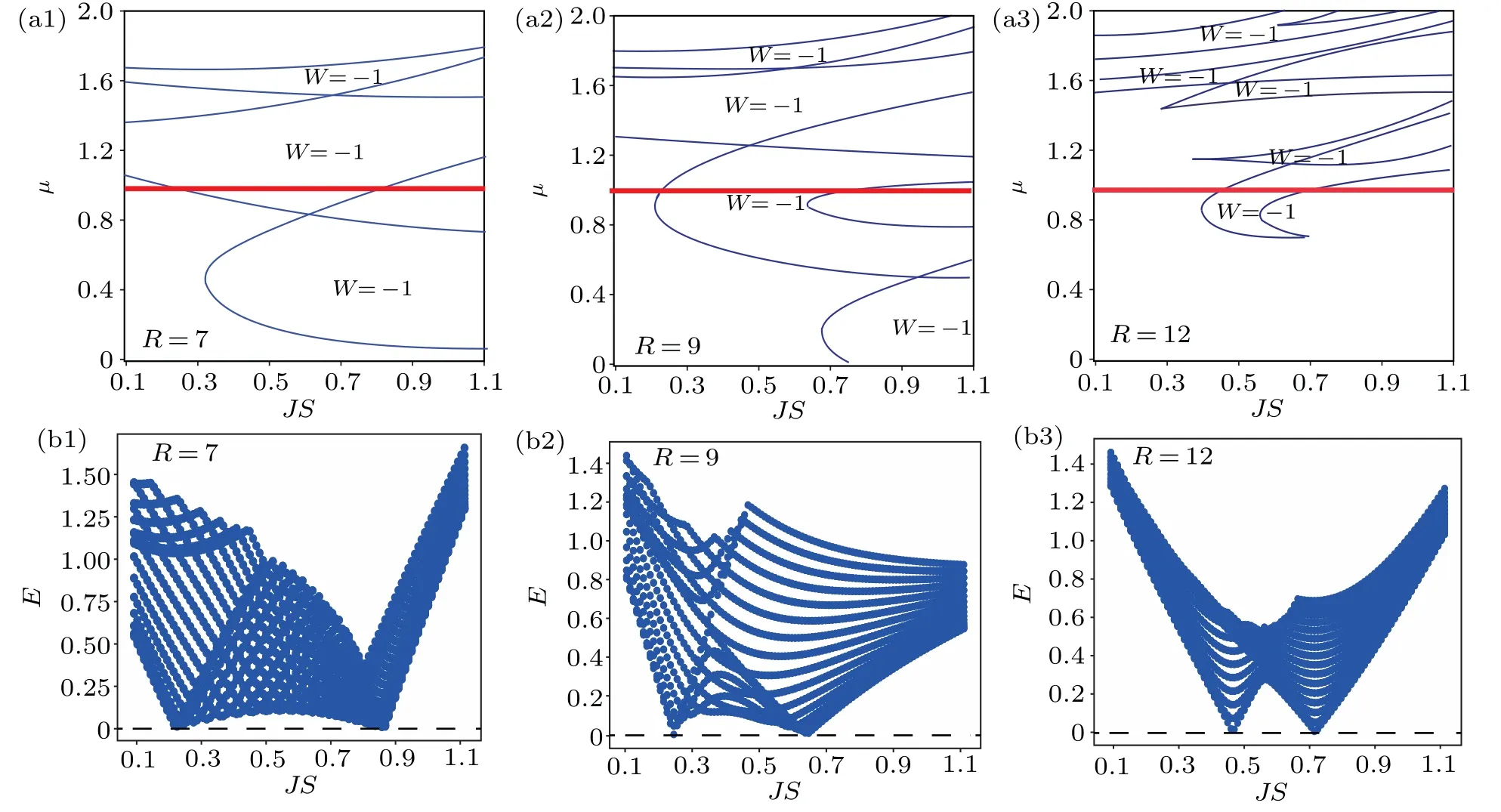
Fig.2.(a)The topological phase diagram of the system.Blue lines are phase boundaries,and the red lines are for μ=1.Topological non-trivial regions with winding number W =-1 are marked in each figure. (b)The lowest 30 positive eigenvalues for each JS with fixed μ =1,i.e.,the red lines in the corresponding upper panels. The eigenvalues would touch zero in the crossing points of red lines and blue lines in(a).

We also examine the structure of spectra with fixedμ=1,i.e.,the red lines in Fig.2(a). The numerical results are shown in Fig. 2(b). There are only 30 smallest positive eigenvalues shown for eachJS.The dotted line in the bottom of each figure isE=0. We could observe that there would be a gap reopening process accompanied with the topological phase transition,which is consistent with the property of Hermitian topological phase transition.

There is also physical interpretation of the winding number.[25,26]We evaluate the spectral gap of the system under open boundary conditions, and depict it in Fig.3(a). The results are consistent with the topological phase diagram obtained before,and in the region where the spectral gap closes,there would be Majorana zero modes and the system is in the topological non-trivial phase. We also achieve the density distribution of these zero modes as shown in Fig. 3(b). Figures 3(b1), 3(b2), and 3(b3) present the results with parameters(μ=1,JS=0.6),(μ=1,JS=0.4),and(μ=1,JS=0.5),respectively. These parameters are located in the topological non-trivial region. The topological zero modes are sharply localized at the boundary of the system. The oscillation pattern of these zero modes near the boundary is consistent with the theoretical result obtained in Ref.[27]. This bulk–edge correspondence is a strong evidence of the topological property of the system.

Fig.3. (a)The spectral gap amplitude in parameter space. The result is consistent with Fig.2(a). (b)The density distribution of Majorana zero modes. They are localized at the boundary and have oscillation patterns near the boundary.

These results can give some illuminations about the achievement of topological superconductor in cold atomic systems. Also,the strength of induced spin–orbit coupling can be changed by varying the radius of the skyrmion, which is different from the current method of manipulating.

4. Conclusion

We have evaluated the spectrum of the one-dimensional s-wave superconductivity in poximity to a skyrmion lattice,whose radius is commensurate with the lattice constant. The spin–orbit coupling induced by this proximity effect is different from a constant one and lead to a rich topological phase diagram. We also examine the topological invariant of each phase,the corresponding edge states,i.e.,Majorana zero mode, and obtain the bulk edge correspondence. These results could give experimental physicists a new method of manipulating spin–orbit coupling in the realization of topological non-trivial systems.

Acknowledgements

We are grateful to Xiao-Ming Zhao and Fa-Di Sun for fruitful discussions.

Project supported by the National Key R＆D Program of China(Grant Nos.2021YFA1400900,2021YFA0718300,and 2021YFA1400243)and the National Natural Science Foundation of China(Grant No.61835013).