A novel lattice model integrating the cooperative deviation of density and optimal flux under V2X environment

Guang-Han Peng(彭光含), Chun-Li Luo(罗春莉), Hong-Zhuan Zhao(赵红专), and Hui-Li Tan(谭惠丽)

1College of Physical Science and Technology,Guangxi Normal University,Guilin 541004,China

2College of Architecture and Transportation Engineering,Guilin University of Electronic Technology,Guilin 541004,China

Keywords: traffic flow,lattice hydrodynamic model,cooperative deviation

1. Introduction

Currently, the exhaust pollution caused by traffic congestion has become the focus of scholarly attention. Hence,various traffic models, including microscopic models[1–5]and macroscopic traffic models,[6–10]were established by researchers to settle traffic problems. In order to intuitively describe the traffic congestion, Nagatani[11]took the lead in proposing a single lane lattice hydrodynamic model. Since then, some models reflected the essence of the traffic congestions by considering backward looking effects,[12,13]delay effects,[14–21]traffic interruptions,[22–24]prediction effects,[25–28]and drivers’ individual behavior effects.[29–33]For reproducing the real environment, a twolane lattice model of traffic flow with lane change was designed by Nagatani.[34]After that, a growing number of extended two-lane lattice models[35–40]have been provided to describe the traffic dynamics.

In recent years,Tianet al.[41]come up with a new model accounting for the density difference (DD) effect. Subsequently,Guptaet al.[42]developed a two-lane lattice hydrodynamic model with the DD effect. Jianget al.[43]discussed the influence of the DD effect when traffic interruption occured.In addition, Sunet al.[44]and Yanget al.[45]put forward a lattice hydrodynamic model by taking the optimal flux difference effect into account. Changet al.[46]designed a model by considering the anticipation flux difference effect.

The optimal flux is a significant factor to describe the traffic evolution. Under the normal circumstances, the driver always expects to get the uniform optimal flux. But in the actual traffic environment, there is a deviation between the uniform optimal flux and the road actual optimal flux.Similarly,it is an ideal traffic state that the traffic flow is in equilibrium to reach the average density.But in the actual traffic environment,there is a deviation between the actual density and the average density. However, it has not involved the cooperative deviation effect of density and optimal flux in the existing lattice models. With the help of the vehicle to X (V2X) communication technology,it is easier to achieve cooperative deviation effect of density and optimal flux. Therefore, we establish a novel lattice model by integrating cooperative deviation of density and optimal flux,which has great practical significance.

Motivated by the above mentioned views,a novel model with the traffic information deviation is provided in Section 2.The theoretical analysis including linear stability analysis and nonlinear analysis for the new model is discussed in Section 3 and Section 4,respectively. Numerical simulation verifies the theoretical analysis in Section 5. Finally, Section 6 gives the conclusion.

2. The novel lattice hydrodynamic model

At the end of the 20th century,Nagatani firstly suggested the single-lane lattice hydrodynamic model,and the equations were given as follows:

whereρ0andρjrespectively show the average and local density,vjrepresents the instantaneous velocity,andadenotes the sensitivity of the driver.V（ρj+1）expresses the optimal velocity function assumed as

whereρcandvmaxexpress the critical density and maximal velocity,respectively.

Applying the V2X communication technology, we can achieve cooperative deviation information of density and optimal flux. Therefore,we add the cooperative deviation of density and optimal flux (CDDOF) effect to raise a new type of evolution equation

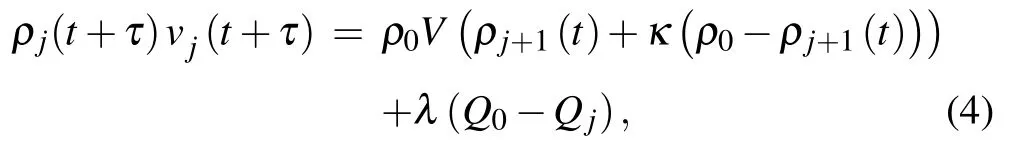
whereκ（ρ0-ρj+1(t)）represents the density deviation effect andκmeans a coefficient that reflects the influence of density deviation.Q0=ρ0V(ρ0)andQj=ρjV(ρj).λ(Q0-Qj)expresses the optimal flux deviation effect andλis a coefficient corresponding to the optimal flux deviation. By eliminating the speedvin Eqs.(1)and(4),the density equation of the new model is gained as

3. Linear stability analysis

The road condition is supposed as uniform traffic flow forρ0andV(ρ0). Then, the solution of the steady-state of uniform traffic flow can be expressed as

Theyj(t) is assumed to be a small disturbance on latticej.Then the instantaneous density can be described as

Substituting Eq.(7)into Eq.(5)and linearizing it,we get

Supposingyj(t) = exp(jik+zt) and substituting it into Eq.(8),we get the expression aboutz

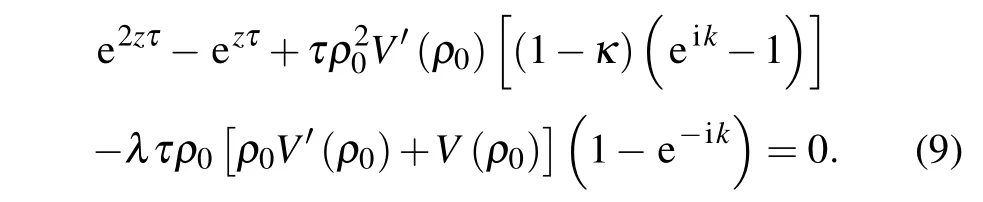
Insertingz=z1(ik)+z2(ik)2+···and substituting it into Eq.(9),we obtain the coefficient of ikas

Whenz2＜0,the uniformly distributed steady-state traffic flow becomes unstable under the interference of small disturbances.On the contrary,whenz2＞0,the uniformly distributed steadystate traffic flow is in a stable state. Therefore,the neutral stability state with the CDDOF effect is acquired

Consequently,the stability condition of the traffic flow can be obtained as

According to the different parametersκandλin Eq.(12),we can describe the density-sensitive phase diagram of the new model. And every solid line has vertices (ρc,ac), which is called the critical point. In Fig. 1(a), whenκ=0 andλ=0 corresponding to the Nagatani’s model, it indicates that the CDDOF effect is not involved. From Fig.1,with the increase of parametersκandλ, the critical point keeps moving down and the stability area gradually expands.It is indicated that the CDDOF effect can effectively promote the traffic flow falling into stable state.

Fig.1. Neutral stability curve.

4. Nonlinear analysis

In this part,we gain the mKdV equation around the critical point(ρc,ac)via nonlinear analysis.First of all,we need to assume a small scaleε(0＜ε ≪1)forjandt. Subsequently,the slow variablesXandTare defined as follows:

wherebis a constant. Then,we can express the densityρj(t)as below:

whercs the critical density near the critical point. By substituting Eqs.(14)and(15)into Eq.(5),the following equation of theεis gained:

The coefficientsgi(i=1,2,...,5)are listed in Table 1. In addition, the following variable transformations are introduced to infer the standard mKdV equation

By ignoring the correction termO(ε),the kink–antikink soliton solution is obtained as below:

Table 1. The coefficients gi (i=1,2,...,5).

wherecis the propagation velocity of the kink–antikink soliton solution,which is deduced from the following condition:

Then,the corresponding solution is given by

Consequently,the amplitudeAis

5. Numerical simulation

Subsequently, the initial conditions are adopted for numerical simulation scene under periodic boundary conditions as follows:

whereρ0is the average density and other parameters are chosen asN=100,ρc=ρ0=0.25,Vmax=2,anda=2.5.

5.1. Spatiotemporal evolution of density

Figures 2 and 3 show the three-dimensional spatial evolution of density aftert=10000 time steps. Figure 2(a) corresponds to the Nagatani’s model. Obviously, asλandκincrease,the density wave amplitudes in the two sets of pictures show a downward trend. In addition, the kink–antikink density waves appear and the density wave propagates to the back of the road in both Figs.2 and 3. In a word,the CDDOF effect can well improve the stability of traffic flow.

Figure 4 describes the density distribution at time stepst=10300.The amplitude of the density wave decreases as the coefficientsλandκincrease. Whenλ=0.04 andκ=0.12,the traffic system presents a uniform flow state. From Fig.4,the CDDOF effect can restrain the traffic congestion.

5.2. Hysteresis loop

Moreover,the hysteresis loop is composed of the density and flux as shown in Fig.5.The stability of the traffic flow can be judged according to its area. As the area increases,the stability of the traffic flow gradually weakens. In Fig.5(a),withλ-value ascending, the area of the hysteresis loop becomes smaller. Figure 5(b)demonstrates the hysteresis loop whenκincreases atλ=0.03. According to Fig.5(b),whenλ=0.03 andκ=0.15, the hysteresis loop converges to a point. It is shown that the CDDOF effect promotes the traffic stability.

5.3. Energy consumption and pollution emission

At present, people still choose fuel vehicles as a means of transportation. Then,the problem of excessive energy consumption cannot be underestimated. Under the extremely severe environmental situation, researchers begin to study how to effectively control the energy consumption and pollutants emission. Therefore, Rakhaet al.[47]offer a model to study vehicle’s fuel consumption and emission as below:

where MOEeis the instantaneous fuel consumption or emission rate(L/s or mg/s),andis the regression coefficient in Table 2,which is applied by Tanget al.[48]

Figures 6–9 show the fuel consumption rate and CO,HC,and NOxemission rate during a period of time for the 25th lattice. Whenλincreases atκ=0 in Figs.6(a)–9(a),the fuel consumption rate and pollutant emission appear a downward trend.Besides,it can be seen from Figs.6(b)–9(b),by increasing the coefficientκ-value, the curve also decreases significantly. In conclusion, by considering the CDDOF effect, not only can the new model effectively reduce fuel consumption,but also cut down vehicle pollutant emission rate.

Table 2. The coefficient .

Table 2. The coefficient .

Fuel CO HC NOx Ke 0,0 -0.679439 0.887447 -0.728042 -1.067682 Ke 0,1 0.135273 0.148841 0.012211 0.254363 Ke 0,2 0.015946 0.030550 0.023371 0.008866 Ke 0,3 -0.001189 -0.001348 -0.000093243 -0.000951 Ke 1,0 0.029665 0.070994 0.024950 0.046423 Ke 2,0 -0.000276 -0.000786 -0.000205 -0.000173 Ke 3,0 0.000001487 0.000004616 0.000001949 0.000000569 Ke 1,1 0.004808 0.003870 0.010145 0.015482 Ke 1,2 -0.000020535 0.000093228 -0.000205 -0.000131 Ke 1,3 5.5409285×10-8 -0.000000706 0.000000618 0.000000328 Ke 2,1 0.000083329 -0.000926 -0.000549 0.002876 Ke 2,2 0.000000937 0.000049181 0.000037592 -0.00005866 Ke 2,3 -2.479644×10-8 -0.000000314 -0.000000213 0.00000024 Ke 3,1 -0.000061321 0.000046144 -0.000113 -0.000321 Ke 3,2 0.000000304 -0.000001410 0.000003310 0.000001943 Ke 3,3 -4.467234×10-9 8.1724008×10-9 -1.739372×10-8 -1.257413×10-8

Fig.2. The space–time evolution of density after t=10000 time steps.

Fig.3. The space–time evolution of density after t=10000 time steps.

Fig.4. The density distribution diagram at t=10300 time steps.

Fig.6. Fuel rate of the 25th lattice.

Fig.7. The CO emission rate of the 25th lattice.

Fig.8. The HC emission rate of the 25th lattice.

Fig.9. The NOx emission rate of the 25th lattice.

6. Conclusion

In this article, the orresponding lattice model is established by considering th CDDOF effect under the V2X environment. According to the theoretical analysis, we find that the CDDOF effect has an excellently positive effect on the stability of traffic flow. On the one hand, by observing the changes of density waves and hysteresis loops,the new model has the effect of enhancing the stability of traffic flow.Furthermore,by analyzing the changes of the energy consumption and exhaust emission,it is found that the CDDOF effect can reduce fuel consumption and exhaust emission.The results of the theoretical analysis and numerical simulation show that the new model can effectively solve the problems of traffic congestion and exhaust emission in the current traffic environment.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No. 61963008), Guangxi Natural Science Foundation (Grant No. 2022GXNSFDA035080),Guangxi Innovation-Driven Development Special Fund Project (Grant No. GUIKEAA19254034-3), and Doctor Scientific Research Startup Project Foundation of Guangxi Normal University,China(Grant No.2018BQ007).