Chiral lateral optical force near plasmonic ring induced by Laguerre–Gaussian beam

Ying-Dong Nie(聂英东), Zhi-Guang Sun(孙智广), and Yu-Rui Fang(方蔚瑞)

School of Physics;DUT-BSU Joint Institute,Dalian University of Technology,Dalian 116024,China

Keywords: lateral optical force,chiral force,chiral sorting,surface plasmon

1. Introduction

Single-beam gradient force trap which is commonly known as optical tweezers has been widely used in the capture of micron-scale particles due to its contactless and nonintrusive characteristics.[1–3]Traditional optical tweezers rely on lens with a large numerical aperture focusing to produce a large light field gradient. However, the capture of nanoscale particles and metal particles still faces challenges[4,5]because of the minimum level of the focused spot size limited by the diffraction limit and the strong scattering in the visible range by noble metal particles.[6–10]As the surface plasmon can be tuned effectively by the size and shape of nanostructure,plasmonic nano tweezers such as waveguides,[11–13]photonic crystal resonators,[14]and other kinds of plasmon optical tweezers,[15,16]have been developed. It has greatly enriched the connotation of optical tweezers.

Chiral objects are also called enantiomers,[17]referring to the property that an object and its mirror cannot coincide in space. At the microscopic level, the molecular configuration affects its dipole moment, leading to active response.[18,19]Separation of chiral molecule is an extremely important process in the pharmaceutical and chemical industries. Recently,optical lateral force and optical enantiomer separation have attracted much attention due to the emergence of abundant abnormal optical force phenomenon.[20,21]Chan and Wang theoretically proved that the electromagnetic near-field coupling caused by dielectric or metal interface can cause transverse optical force perpendicular to the wave vector to act on chiral particles.[22]In addition, the direction of optical lateral force is related to the sign of particle chirality. Many researches have shown that linearly polarized light,[23]circularly polarized light,[24]or vector hollow light beams[25]can be used to separate chiral particles, which confirms the feasibility of the full optical sorting of enantiomers. However, in their researches,the metal and dielectric interfaces each were usually considered as an infinite plane, and the sorting effect that is produced by a finite-size metal structure was ignored. Additionally,the energy density of the plane wave is uniform in the vertical direction of the wave vector, so it is necessary to use an oblique incidence on the substrate to generate exogenous chirality. This brings another problem that the radiant optical force in the direction of light propagation is difficult to eliminate.

Spin angular momentum (SAM) and orbit angular momentum(OAM)have been known to possess important characteristics caused by light polarization and energy flow since the vector beam was established by Allenet al.[26]The socalled vector beam is actually a structured light field with a non-uniform distribution of light polarization on the beam section with quite flexible and customizable characteristics producing a richer light–matter interaction phenomenon.[27]From the perspective of momentum transfer,[28]the SAM and OAM contained in the vector beams provide a route for the multidimensional manipulation of particles. In this consideration,we propose the combination of the vector beam and the plasmonic structures. On the one hand, the interaction between vector beam and noble metal can excite different modes by adjusting the wavelength of incident wave and the size of the micro-nano structure. On the other hand, the near-field enhancement effect can increase the gradient of the light field.The spatial light field control of the micro-nano structure and the electromagnetic field enhancement caused by local surface plasmons can produce the equivalent effect acting as the lens.Thus,the problem of difficulty in obtaining a large sorting area by using lens can be solved. The new interaction generated by the vector beam and the micro–nano structure can provide a larger sorting area than the traditional optical tweezer relying on the focused beam, which helps to achieve the capture and sorting of chiral particles at the same time.

2. Simulation model

A typical vortex Laguerre–Gaussian (LG) beam in the cylindrical coordinate system in the paraxial approximation is used. The complex scalar function describing the distribution of the field amplitude can be expressed as follows:

andZR=/2 is the Rayleigh range, in whichk=nk0=n(2π/λ0). TheR(z)=z[1+(zR/z)2]is the radius of curvature of the beam’s wavefronts atz,and(2p+|l|+1)tan-1(z/zR)is the Gouy phase atz.

The representation of a radially polarized LG laser mode is achieved by using the vector potential

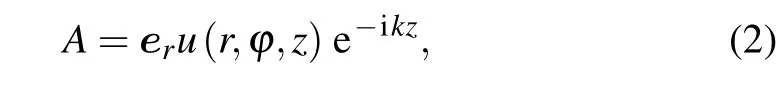
with the transformation relationship between the rectangular coordinate system and the polar coordinate system:

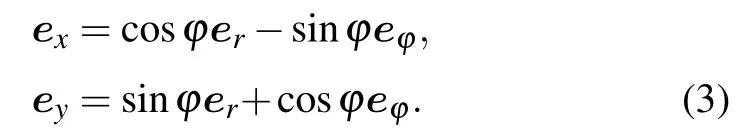
The definition in Cartesian coordinate system can be obtained as follows:

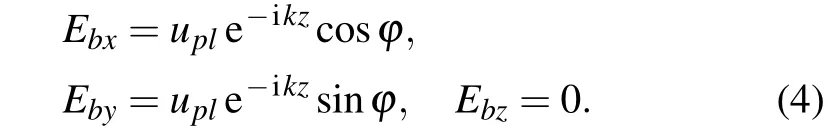
In Fig.1(a),the energy and polarization distribution of the radially polarizedu01LG beam consists of a ring shape light field with zero field amplitude in the center of the beam. The electric field has only radial component. Figure 1(b) shows the distribution of the isophase surface of the radial electric field with a shape of vortex, and the energy propagates along thezdirection. Figure 1(c) represents the schematic diagram of the simulation system. In order to satisfy the paraxial condition in the entire system, the beam center is set to be(x,y,z)=(0,0,0). The media are a glass cover atz ＞0 and water atz ＜0, respectively. The height of the gold ring is h and its diameter isd=1 μm. The thickness of the ring sidewall is initialized to 80 nm. A chiral medium sphere with a radius of 20 nm is attached near the outer side of the gold ring,with the refractive indexn=2.The advantage of the nano ring lies in the centrosymmetry of its structure,especially when it is illuminated by vector beams. It can avoid mismatching the electrical field gradient with other kind of structures. When the LG beam that propagates in thezdirection is irradiated on the ring,the chirality of particles breaks the mirror symmetry of the space and thus generates optical force perpendicular to the direction of light propagation, which is called the optical lateral force. In our system, we define that the optical lateral force has an azimuthal orientation ofφin the polar coordinate system.

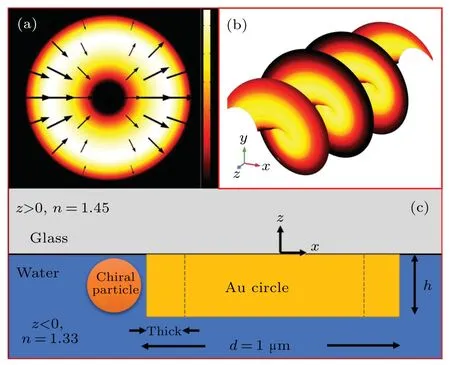
Fig.1. (a) Polarization and energy distribution of radially polarized Laguerre–Gaussian beam at the beam waist. (b) Isophase distribution map of Eρ component of LG beampropagating along the z direction. (c)Overall schematic diagram of simulation structure,with media being dielectric layer at z ＞0 and water at z ＜0 and a gold ring circle with radius of d/2 and height of h attached to the dielectric layer. The position of the particle is near the outer side of the gold ring.Considering that the system has central symmetry,the position of the chiral ball is set to be(x,y,z)=(xposi,0 nm,-30 nm).

Numerical simulations are performed with full-wave calculation by using a commercial finite element method software package(COMSOL MULTIPHYSICS 5.5). By solving the electromagnetic field around the particle and according to the Maxwell stress tensor(MST)theory,the force that acts on the particle can be calculated from

3. Results

In the visible range, the illumination causes the electric field to be strongly enhanced, which can be artificially customized by adjusting the geometric parameters of the gold ring structure. According to the MST theory,the force directly relates to the electromagnetic field distribution on the surface of the particle. Therefore, the size of gold ring and the background field distribution around the particle should be adjusted firstly. Figure 2(a) shows the scattering cross section of the gold ring with height in a range from 20 nm to 90 nm as a function of wavelength under LG beam (withu01) illumination. As the height of the ring increases, the main resonant peaks are blueshifted from 650 nm to 575 nm and the intensity decreases. Figure 2(b) presents the normalized electric modulus spectrum where the particle exists. It can be seen that as the height increases, the enhancement peak of the electric field modulus shifts to the short wavelength side with its amplitude increasing. Figure 2(c) shows the optical force in the radial direction of the particles as a function of incident wavelengthλ. The particle is placed on the outside of the gold ring, so when the radial optical force is negative, the particle will be trapped near the wall of the gold ring. The maximum radial optical force appears at 650 nm at a ring height of 20 nm. Similarly, the peak of radial optical force tends to be blueshifted as the ring height increases. A comprehensive comparison among Figs. 2(a)–2(c) reveals that the resonance frequency of the gold ring scattering, the normalized electric field modulus peak,and the maximum radial optical force that characterize the capture capability have consistent wavelength movement with the ring height.

Fig.2.(a)Scattering cross sections versus incident wavelength.(b)Normalized electric field modulus versus incident wavelength,with particle trapped near the sidewall of gold ring.(c)Radial optical force acting on the achiral particle(solid lines)and chiral particle(dash for κ=0.4,dot for κ=-0.4)as a function of incident wavelength. (d)Lateral optical force acting on achiral particle as a function of the incident wavelength.All the above results are obtained for gold rings with heights of 20 nm,30 nm,40 nm,60 nm,and 90 nm.

Owing to the fact that the background electromagnetic field and the structure of gold are both centrosymmetric, the radial and lateral optical forces have no correlation with theφcoordinate. Therefore,if the radial optical force is positive,the chiral particle will be pushed away from the focus area.On the contrary,if the radial optical force is negative,the particle will be trapped near the sidewall of the gold ring. It should be noted that the chirality of the particle almost has no effect on the redial optical force (Fig. 2(c)). The sign of the angular optical force represents the direction that the chiral particle rotates around. From the top view,the positive angular optical force indicates that the particle will rotate counterclockwise around the gold ring and vice versa.The solid lines in Fig.2(d)represent the angular optical force of the achiral particle as a function of incident wavelengthλ. Because the achiral particle is very close to the gold interface, the optical force is produced by the combined effects of the lateral radiation that is generated by the gold ring scattering and the strong electric field modulus gradient from the plasmon resonance. The angular component is affected by the gold ring excitation mode and shows different signs. Therefore, there will be non-zero lateral optical force acting on achiral particles when the gold ring is excited by its resonance frequency.

In the background electromagnetic field, because of the paraxial approximation and the dismissing of the electric field component in thezdirection, the common light field has no projection component of the Poynting vector in thex–yplane.However, owing to the interaction between the OAM carried by vortex-shaped wavefront of the LG beam and the gold ring,the radial and angular wave vector components which are perpendicular to the propagation direction of the background field will come into being.Figures 3(a)–3(d)show the projection of the relative time-averaged Poynting vector in thex–yplane for the 40-nm-high gold ring with incident wavelength of 500 nm,530 nm,600 nm,and 650 nm,respectively. The coordinate of this plane isz=-30 nm corresponding to the center location of the particle. The color in the figure represents the electric field modulus, and the black arrows in the outer space of the gold ring indicate the relative time-averaged Poynting vector distribution. The direction of energy flow near the interface is clockwise under the conditions of 500-, 530-nm incident wavelengths, while the energy near the interface flows counterclockwise under the conditions of 600-, 650-nm incident wavelengths.

In order to illustrate the influence of light scattering and field gradient on the optical force,Maxwell stress tensoris decomposed intoand[15]and then gradient force and scattering force can be calculated by integrating the tensors

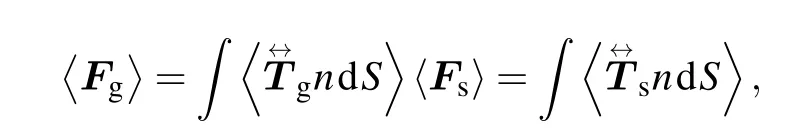
respectively. As shown in Fig.3(e), the blue dash dotted line represents the angular scattering light force acting on achiral particle as a function ofλ. When the wavelength is 500 nm and 530 nm, the angular scattering forces without chiral are both negative, corresponding to the clockwise flow of energy flow in Figs. 3(a) and 3(b). When the wavelength is 600 nm and 650 nm, the angular scattering forces without chiral are both positive, corresponding to the counterclockwise flow of energy flow in Figs. 3(c) and 3(d). The gradient force has two prime peaks (positive and negative) atλ=580 nm andλ=620 nm as the short dotted line shown in Fig. 3(e), in which region the lateral force also becomes largest. The combined effect of scattering force and gradient force leads to the non-trivial and wavelength-dependent lateral total force. Unlike the radial optical force, the chirality of the particle gives a significant offset to the intensity of the angular optical force,especially for the gradient angular force.

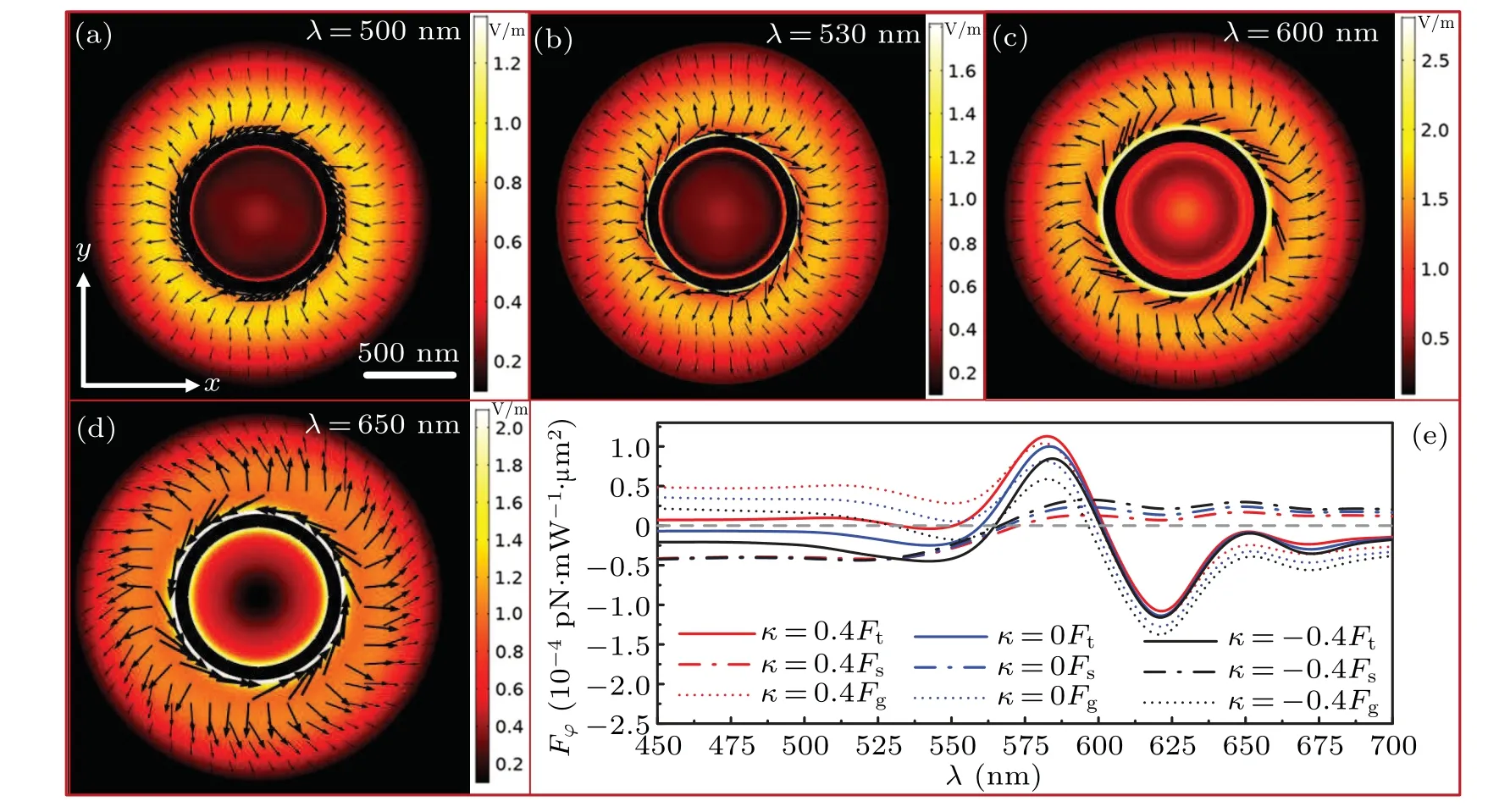
Fig.3. Distributions of electric field modulus and relative time-averaged energy flow vector supported by gold ring with incident wavelength of(a)500 nm,(b)530 nm,(c)600 nm,(d)650 nm. Height of gold ring in each panel[(a)–(d)]is 40 nm. (e)Spectra of optical angular forces of the chiral particle near the side of the gold ring. Solid lines, dashed–dotted lines, and short dotted lines represent the total angular force,scattering angular force,and gradient angular force,respectively.

Fig.4. Numerical results of scattered field of chiral particles near gold ring,The white arrowrepresents relative time-average Poynting vector around chiral particle for(a)κ =-0.4, (b)κ =0 and(c)κ =0.4. The blue arrow indicates the time-averaged electric SAM density for(d)κ =-0.4,(e)κ =0 and(f)κ =0.4. Gold ring height is 40 nm. The center of particle is in the plane at z=-30 nm. Incident wavelength is set to be at λ =500 nm. The color scale is logarithmic modulus of total electric field.

Fig.5. Angular optical forces versus incident wavelength for gold ring height of(a)20 nm,(b)30 nm,(c)60 nm,and(d)90 nm.

Figure 4 shows the near-field numerical results of chiral particles near the gold ring with a height of 40 nm. The white arrow is the relative time-averaged Poynting vector around the particle forκ=-0.4 (Fig. 4(a)),κ=0 (Fig. 4(b)) andκ=0.4 (Fig. 4(c)), which indicates that the relative Poynting vector is distributed around the chiral particle, and the coupling between the chiral particle and the interface results in the asymmetric distribution. The relative Poynting vector around the isolated particle with opposite chirality is mirrorsymmetric.[22]However,the gold interface on one side of the chiral particle breaks this symmetry, resulting in the angular optical force related to the chirality.

The time-average electric SAM density〈Le〉=ε0/(4ωi)(E×E*)], which is one of the important components of the angular force (which will be shown in Eq. (8)),forκ=-0.4,κ=0, andκ=0.4 are shown in Figs. 4(d)and 4(f), respectively. The maximum relative strength appears near the gold interface and points to theydirection.But the direction of the SAM away from the gold interface points to the-ydirection, because the radially polarized LG beam does not carry SAM, and the total angular momentum should be conserved. Moreover, the SAM in the particle is significantly different from the chirality. The difference of the optical SAM from the particle chirality gives rise to the different angular optical forces on the chiral particles. However,the phenomenon of non-chiral particle seems counterintuitive.Although there is SAM in the space where the achiral particle located as shown in Fig.4(e),achiral particle is not subjected to the angular optical force.Figure 4(b)shows that the relative Poynting vector around the achiral particle does not exhibit a vortex phenomenon similar to that the chiral particles present.Therefore,it can be known that under the premise of excluding the strong angular scattering caused by the resonance excitation of the gold ring,the angular optical force on the particles arises from the optical SAM, which is caused by the interaction between the OAM carried by the LG beam and the gold ring.

In order to further discuss the influence of the interaction,figure 5 shows the angular optical forces as a function of wavelength at different gold ring heights. The gradient forceFg,scattering forceFs,and the total angular optical forceFtare all sensitive to the wavelength of incident light. For the 20-nmhigh gold ring (Fig. 5(a)), the magnitude of scattering force and the gradient force are roughly equal whenλis less than 600 nm, and the total angular force approaches to zero under these conditions. For rings with heights of 30 nm(Fig.5(b)),60 nm(Fig.5(c))and 90 nm(Fig.5(d)),the cutoff wavelengths for balancing the gradient force and the scattering force gradually decrease to 570 nm, 530 nm, and 520 nm, respectively,and their differences become larger. When the wavelength is larger than that threshold,the total angular force exhibits more than one peak. Examining all figures together, it can be seen that the scattering force is negative at the short wavelength,and the difference in the scattering force caused by the additional chirality is not obvious. The sign of scattering force is positive at long wavelength, and its zero position is blueshifted as the gold ring height increases. On the contrary,the gradient force is positive at short wavelengths,and it is greatly different for different chiral particles,so the total angular optical forces of opposite chirality at short wavelength have opposite sign. When the wavelength increases, the gradient force becomes negative and its peak comes into being,which is consistent with the scattering spectra in Fig. 2(a). This demonstrates that under an appropriate incident wavelength, the influence of achiral-related angular optical force can be reduced,thus the angular optical force caused by chirality with different sign domain and the directional motion determined by the chiral sign can be achieved. This provides an effective approach to discriminating and separating chiral enantiomers. We can release the mixture of enantiomers in one direction on the outside of the ring and then collect them on the clockwise and counterclockwise sides, respectively. In order to avoid moving chiral particles for more than half a cycle, some physical isolation measures can be used,such as setting a baffle on the other side of the nano ring. Besides we should give priority to gold rings with height greater than 30 nm, because in practical chiral enantiomer separation,both the negative trap radial optical force and large chiral angular optical force difference should be fulfilled in the wavelength range shorter than that threshold.

In the previous parts, it is found that the strong angular scattering of the gold ring and the corresponding achiralrelated angular optical force can be avoided when the incident wavelength is shorter than 500 nm, so the particles with different chirality signs will have the opposite angular optical forces. In Fig. 6(a), the effect of the chirality parameter on the radial optical force and angular optical force are illustrated. It can be inferred that when the chirality number is zero, the radial force tends to be the maximum, and there is little difference in radial force for chirality parameters with different signs. Although the polarization of radially polarized LG beam exhibits rotational symmetry,its inherent OAM leads to imperfect symmetry of the angular force acting on particles with opposite chirality. Therefore,the above mentioned opposite angular optical forces exist in a relatively large chirality parameter range. Figure 6(b)shows that the magnitudes of radial force and angular force acting on particles(κ=0.4,0,-0.4)decrease as the gap distance between the chiral particle and the side of the gold ring increases, indicating that the force is due to the coupling between the particle and the gold interface. The radial forces with different chirality are roughly the same,and point to the center of the gold ring,which shows that particles within a limited range of the gap distance will be affected by the radial optical trap.

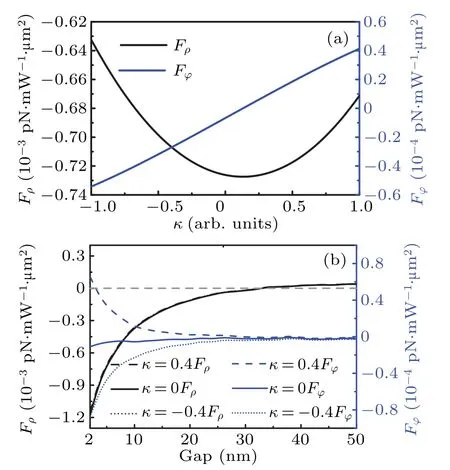
Fig.6. (a)The radial force and angular force acting on a 20-nm-radius chiral particle versus(a)chiral parameters and(b)gap distance between the particle and the ring side,with incident wavelength being 500 nm and gold ring’s height 60 nm.

The results shown up to now are full-wave simulations of chiral balls. In order to explain the origin of the chiral angular force intuitively, we consider the configuration of the dipole chiral particle on the ring side. This analytical expression can be used for evaluating the origin of angular optical force and providing an immeasurable role in optimizing the parameters.The induced dipole moments of such a chiral particle can be expressed as follows:[22,33]

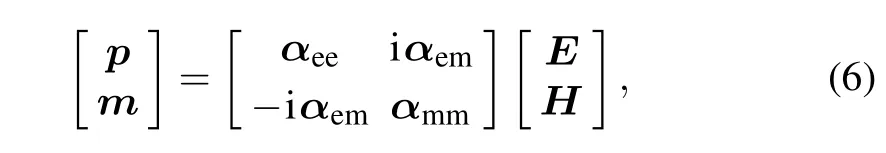
wherepandmare the electric and magnetic dipole moment,respectively,EandHare the electromagnetic fields acting on the particle.For a chiral dipole with radiusa,theαee,αmmandαemin Eq. (6) are the electric, magnetic and isotropic mixed electromagnetic dipole polarizabilities,respectively,which are composite functions of relate permittivityεp, relative permeabilityμp,and chirality parameterκ. According to the vector formula of the optical force acting on a dipole particle, the following formula is obtained:

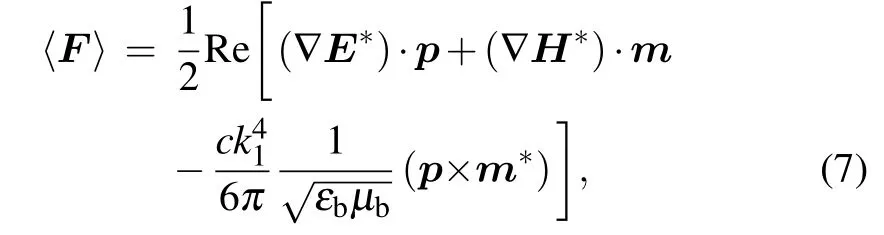
wherek1=nb2πλ/cis the wave number andnb=is the refractive index of the background material.

Substituting Eq.(7)into Eq.(8),the expression of the optical force can be written as

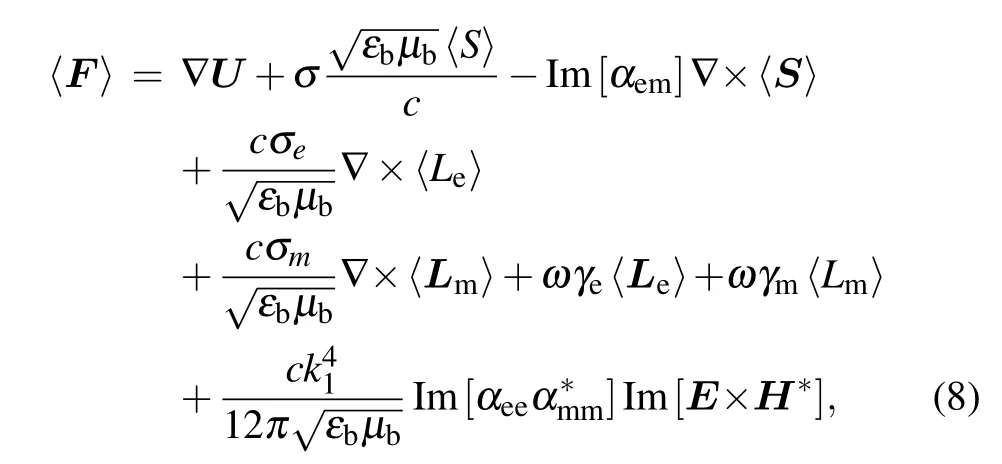
with the optical potential

The time-averaged Poynting vector〈S〉=(1/2)Re(E×H*),the electric SAM density〈Le〉=(ε0/4ωi)(E×E*) and the magnetic SAM density〈Lm〉=(μ0/4ωi)(H×H*),and the cross sectionsγe,γm,σe,σm(shown in Section 5).

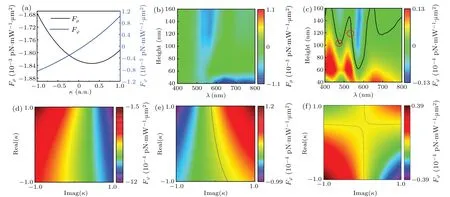
Fig.7. (a) Radial force and angular force as a function of κ at wavelength λ =500 nm. (b) Radial and (c) azimuthal force acting on achiral particle as a functions of gold ring height and incident wavelength. (d)Radial force as a functions of real part and imaginary part of κ,when gold ring height is 120 nm and λ is 530 nm. (e)Azimuthal force as a function of complex κ when gold ring height is 100 nm and λ is 500 nm. (f)Azimuthal force as a function of complex κ when gold ring height is 120 nm and λ is 530 nm.

Figure 7(a)shows the radial force and angular force as a function ofκat wavelengthλ=500 nm in the dipole approximation. It is clear that the relationship between radial force and chirality and between angular force and chirality are similar to those calculations from the full-wave simulations for the same size chiral particle as shown in Fig.6(a).More generally,κconforms to the inequalityκ2＜εrμr.[30]The real part and imaginary part of the chirality parameterκare related to optical rotation and circular dichroism,[33]respectively. In order to take advantage of the differential radial force added by the chirality,the absolute value of radial force acting on the achiral particle should be as low as possible. Figures 7(b)and 7(c)show that the radial force and angular force acting on achiral particle are both a functions of gold ring height and incident wavelength. Figure 7(b) indicates that in dipole approximation,the radial optical force is obviously enhanced when illumination wavelengthλis in a range of 520 nm–580 nm,thus it can be concluded that the ability of the gold ring to capture the particles indeed increases in the resonance excitation mode. However, the shift of the peak position is not obvious with increase of the ring height, this may be due to the fact that the particle is idealized as a point,and its coupling modes with the upper and lower boundaries of the gold ring are ignored. The black solid line in Fig.7(c)represents the contour line when the radial force is zero,and indicates the relationship between the gold ring height and the wavelength suitable for optical sorting. When the height is 120 nm andλis 530 nm,the radial force as a function of real part and imaginary part ofκis shown in Fig.7(d). The chiral parameters will affect the amplitude of the radial force,that is,the capture stiffness,but the sign of the radial force does not change. Obviously, the imaginary part of the chiral parameter has much larger influence on the radial optical force than the real part. The angular force as a function of complexκunder the condition of height 100 nm andλ500 nm,and height 120 nm andλ530 nm are shown in Figs. 7(e) and 7(f), respectively. The dashed lines represent the contour line when the radial force is zero. The difference in contour line between those two figures indicates that different gold ring scattering modes are excited.

4. Methods

4.1. Method of simulating total force, gradient force and scattering force acting on chiral particles

In our simulation, the properties of chiral nanospheres are determined byεr=4,μr=1,r=20 nm, and the chiral parameterκ. The gap distance between the edge of chiral nanosphere and the upper glass cover and between the edge of the chiral nanosphere and the side of gold ring are both 10 nm(unless otherwise mentioned). Using the integral of the timeaveraged maxwell stress tensor:

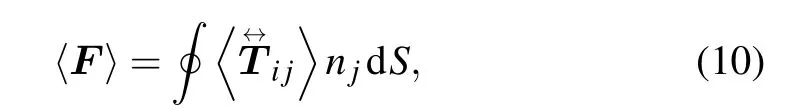
where dSis the integral surface andnjdenotes the unit normal perpendicular to it. The maxwell stress tensor is expressed as

Normally, the MST theory only gives the total force exerted on a particle. In our system, we decompose the total electromagnetic force into gradient force and scattering force based on the MST theory. The source of the optical force is the electromagnetic force and the Lorentz force,specificallyf=ρE+J×B. The gradient force related to the electric field and the scattering force related to the magnetic field are given below:[15]

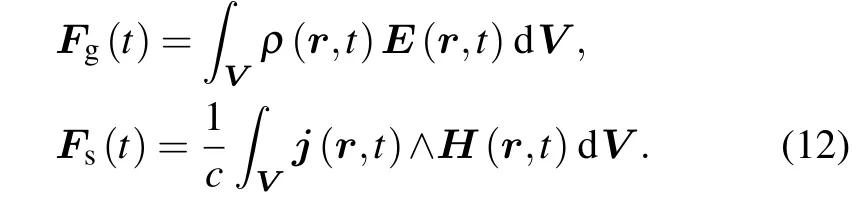
Then we can calculate the gradient force and the scattering force by integrating the tensors:

where

4.2. Numerical method of calculating polarizability of chiral dipole

4.2.1. Mie scattering coefficients

Mie scattering coefficientsan,bn,cncan be expressed as follows:[25]

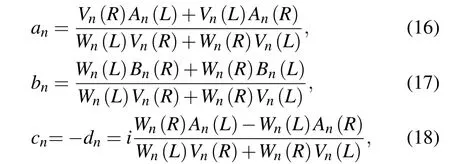
where

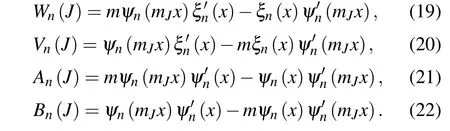
HereJ= L,R andx=k0a.ψn(ρ) =ρjn(ρ)ξn(ρ) =(ρ),with jn(ρ)being the spherical Bessel functions and(ρ)being the spherical Hankel functions of the first kind.The relative refractive indicesmLandmR, and the mean refractive indexmare expressed as

andm=(mL+mR)/2.[21]It should be pointed out that in our work, the chiral particles are small, we retain only the term ofn=1. Thus the polarizabilitiesαee,αmm, andαemfor the spherical chiral particle are obtained from its Mie scattering coefficients as follows:

Here,εrandμrdenote the dielectric properties of chiral particles.

4.2.2. Cross sections

The cross sections can be expressed as

5. Conclusions

In summary, we have numerically shown that the LG beam as a typical vector beam can induce angular optical force for the chiral particle close to the plasmonic gold ring. The radial optical force is related to the resonance excitation of the gold ring, and it is able to make the particle trapped near the vertical interface of the gold ring. The angular optical force,which is also known as optical lateral force associated with the chiral-interface interaction and arises from the optical SAM caused by the interaction between optical OAM and gold ring structure, is sensitive to the sign of the chirality parameter.However, it is necessary to note the strong angular scattering of the gold ring in a certain wavelength range. It can induce a non-chiral related angular optical force,which might be larger than the azimuthal optical force caused by optical chirality.The scattering induced angular optical force can be avoided by selecting a specific incident wavelength,and then the chiral related azimuthal optical force can induce an opposite orbital rotation of the trapped particles with chirality of different sign near the gold ring. Our work presents a potential approach to catching as well as separating chiral enantiomers.

Data availability

Some specific data not given in the results in this paper can be obtained from the authors if the reader needs them.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 12074054) and the Fundamental Research Funds for the Central Universities,China(Grant No.DUT21LK06).