具有边界反馈控制弱耦合梁-弦系统的稳定性
章春国,刘维维,张海燕(杭州电子科技大学数学系,浙江杭州310018)
具有边界反馈控制弱耦合梁-弦系统的稳定性
章春国,刘维维,张海燕
(杭州电子科技大学数学系,浙江杭州310018)
研究具有边界反馈控制的弱耦合梁-弦系统.首先在合适的假设下,应用线性算子半群理论证明了系统的适定性;进而运用线性算子半群的频域定理证明了具有边界反馈控制的弱耦合梁-弦系统的能量是一致指数衰减的.
梁-弦系统;线性算子半群;边界反馈控制;一致指数衰减
1 引言
近年来,梁-弦系统在空间科学及机器人学中有着广泛的应用,研究梁-弦系统的稳定性既有理论指导意义,又有实际工程意义.材料科学的发展为弹性结构的抑振提供了新的方法,随着应用的需要,许多数学与力学工作者研究了具有各类阻尼的Euler-Bernou lli梁,Tim oshenko梁,Ray leigh梁系统的稳定性,其中主要方法运用算子半群理论与乘子技巧.例如:文献[1]研究的是非线性耦合振动的Petrovsky系统,文献[2-9]考虑的是具有各种不同阻尼的梁与弦系统的稳定性,利用能量函数结合乘子技巧得到了系统能量的指数衰减性和多项式衰减性.本文考虑一类具有边界反馈控制的弱耦合梁-弦系统的稳定性.更具体地说,研究如下一类弱耦合系统的初边值问题:
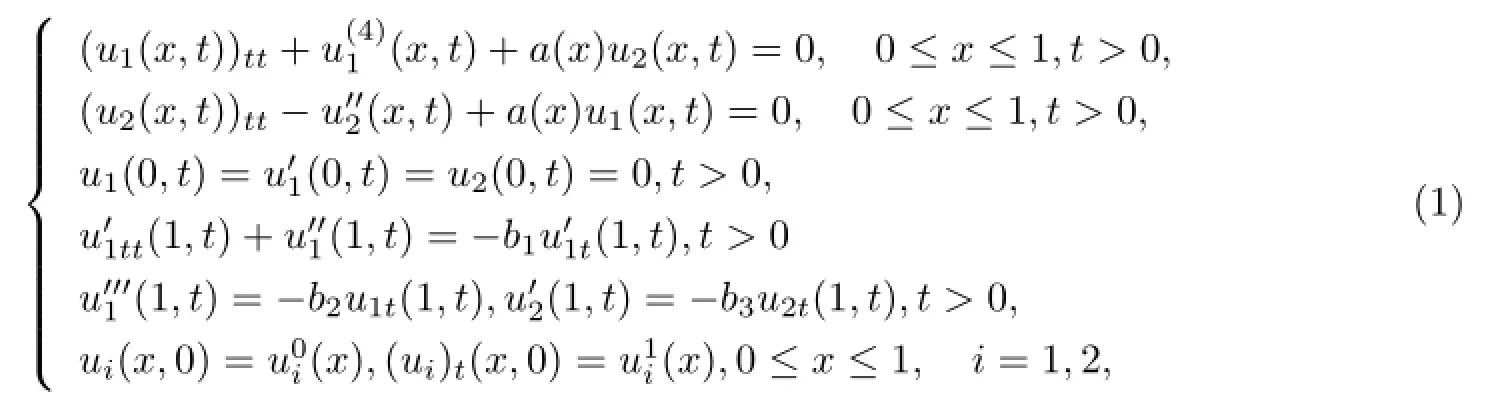
其中′表示对空间变量x的导数,反馈常数bi>0,i=1,2,3,a(x)∈L∞(0,1).
本文的主要想法源于文献[5]和[6],并根据经典结果[10]和频域结果[11-12],运用分片乘子技巧获得了系统(1)的稳定性.
2 预备知识基本假设
引入函数空间

赋予范数

因此V和H都是实(复)Hilbert空间.

则W也是实(复)Hilbert空间.
接下来,定义W上线性算子A如下:

于是将系统(1)改写成W上的抽象Cauchy问题


定义系统(1)在时刻t的能量为

其中Poincaré常数c1,c2>0,Hk(0,1)是k阶Sobolev空间(参见[13]).
为了研究系统(1)的稳定性,作如下假设:

这里‖a‖∞=‖a‖L∞(0,1)>0.

引理2.1(见[11])设A是Hilbert空间H上的压缩C0-半群eAt的无穷生成元,则eAt指数稳定的充分必要条件是:

3 主要结果
定理3.1如果假设(H)成立,那么A是W上压缩C0-半群eAt的无穷小生成元.进一步,若(u01,u02,u11,u12,(u11)′(1))∈D(A),则系统(1)存在唯一的强解;若(u01,u02,u11,u12,(u11)′(1))∈W,则系统(1)存在唯一的弱解.
证对于∀(u1,u2,v1,v2,y)∈D(A),分部积分并应用边界条件得
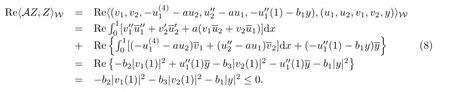
因此,A在W中是耗散的,易证KerA={0}.

于是

将(10)中的三、四两式分别乘以u1和u2,并在(0,1)上积分,分部积分得
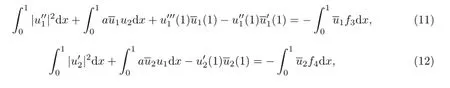
将(11)和(12)两式相加得

和

将(15)代入到(14),并由(5)得

(13)结合(16),应用带ε的Cauchy不等式得

于是

从而

再一次利用(5)得

其中,c=m ax{c1,c2}.

结合(20),(21)和(22),存在某个常数M>0,使得

因此A-1∈L(W),且0∈ρ(A)(A的预解集),于是A是闭的.再由预解式的连续性知,对于足够小的λ>0,算子λI-A的值域rg(λI-A)=W.由定理1.4.6(见[10])得D(A)=W.应用Lum er-Phillips定理,线性算子A是W上压缩C0-半群eAt的无穷生成元.
在给出定理3.2之前,先给出线性算子A的谱性质.
性质3.1如果假设(H)成立,那么ρ(A)⊃iR={iλ|λ∈R}.
证首先证明A具有紧的预解式.不妨设{Yn|n≥1}⊂W是一有界序列:即‖.由定理3.1的证明过程知0∈ρ(A).因此令,由Sobolev嵌入定理得Zn存在收敛子列,所以A-1是紧的.
接下来证明ρ(A)⊃iR.由于A-1是紧的,A只有点谱.
不妨假设λ∈R(λ/=0)使得iλ∈σP(A)(A的点谱),于是存在Z=(u1,u2,v1,v2,y)/=0使得(iλI-A)Z=0,即

由于

由(23)和(24)得
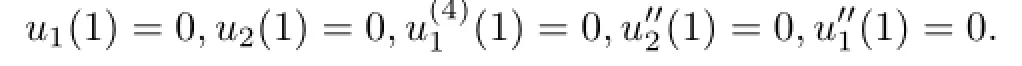
再由(2)知:由常微分方程初值问题解的唯一性定理得(u1,u2)=0,因此Z=(u1,u2,v1,v2,y)=0,这与Z/=0矛盾,性质3.1得证.
定理3.2若假设(H)成立,则压缩C0-半群eAt是指数稳定的.
证设u1=u1(x,t),u2=u2(x,t)是系统(1)的解,那么

由引理2.1和性质3.1,要证明定理3.2,只需证明
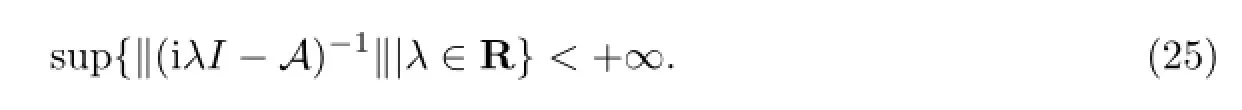
假设(25)不真.即sup{‖(iλI-A)-1‖|λ∈R}=+∞,由共鸣定理和预解式连续性知,存在{λn}⊂R和使得

用(v1n,v2n)对(28)在H中作内积,
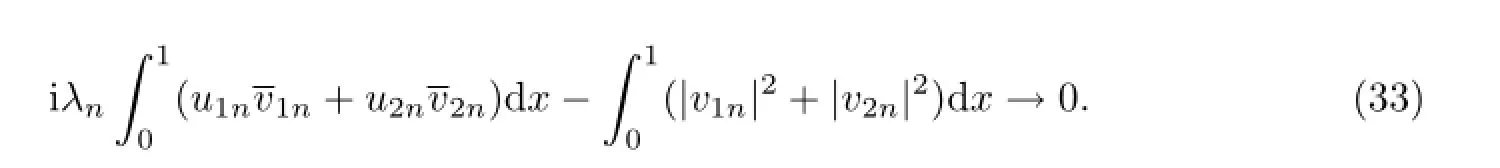
用(u1n,u2n)对(29)在H中作内积,并分部积分得
学校的作息时间与农业生产相匹配,也分为一天三节,每周上6天课。因为没有统筹,许某上一天课就算一天工,周日不出工就没有工分。生产队开始只给他评了三级工——9分,因为“我们还是后生,做不了多少,体力没有多少,一级一般要担得100多斤,我们一般是三级,四、五级一般是老人或者是妇女。如果一个月有四个星期日你没参加生产劳动,就少了36分。”(XJA170325)可见教师与社员一样,对工分都是非常重视的。

将(33)和(34)两式相加并取实部得

由(28)知:在L2(0,1)中,u1n→0,u2n→0.因此(35)改写为
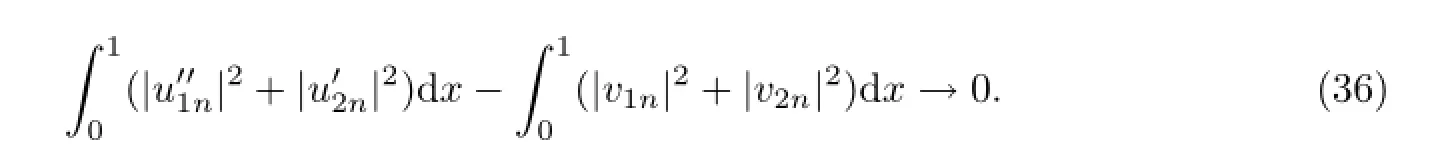
上式结合(26)得

将(28)代入(29)得

现取乘子q(x)=eηx-1,其中η>0是一个给定常数(它的取值后面给出).

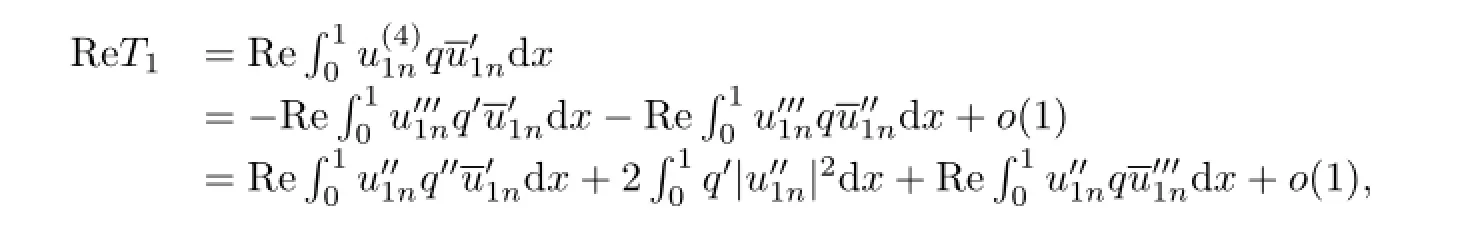
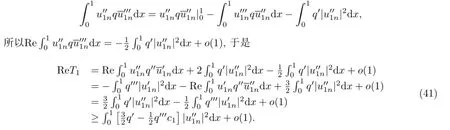
由(28)立即得到:
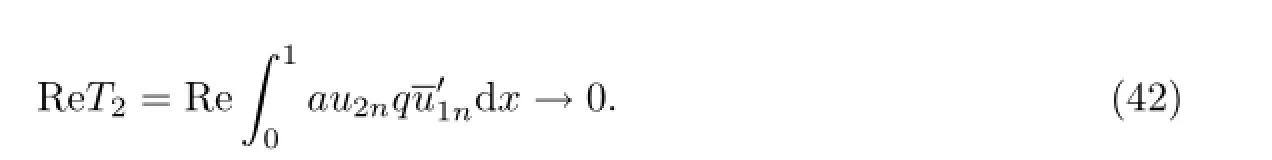
由(28)和(31)得到

上式结合(41)和(42)有


由于q(0)=0,结合假设(H),(5)和(31),分部积分并取实部得

又由(28)立即得
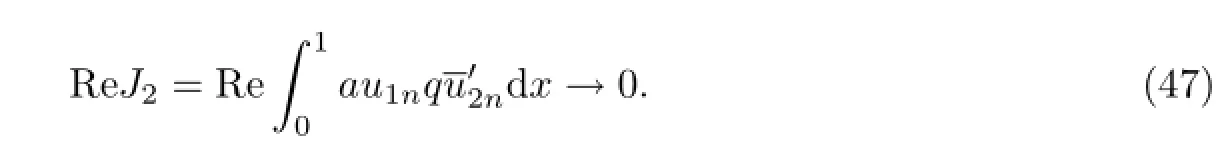
又由(28)和(31)得
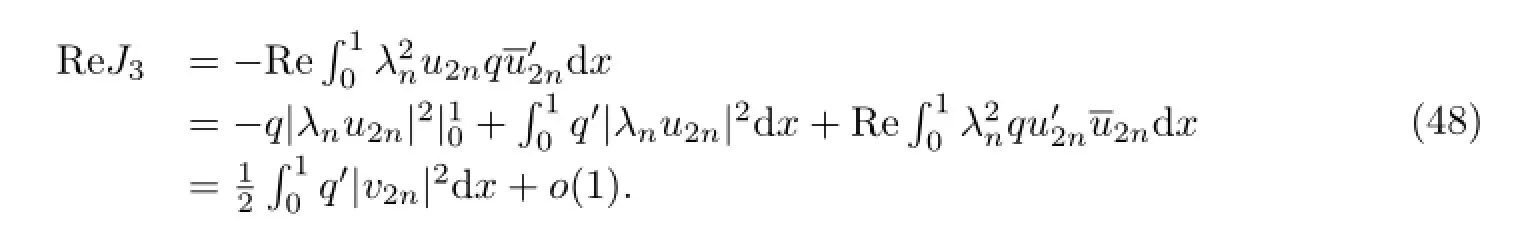
上式结合(46)和(47)有
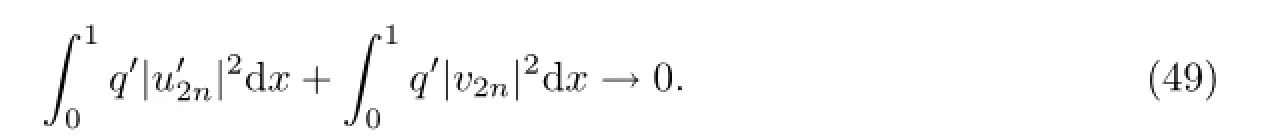
由(44)和(49)相加得

现在只要取常数η>0使得
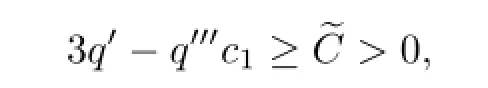

容易看出,上式与(37)矛盾.因此(25)成立,从而证明了定理3.2.
[1]Han Xiaosen,Wang M ingxin.Energy decay rate for a coup led hyperbolic system w ith non linear dam p ing[J].Nonlinear Anal,2009,70:3264-3272.
[2]A issa G,Salim A.M essaoud i.General energy decay estim ates of T im oshenko system s w ith frictional versus viscoelastic dam ping[J].M ath M eth Appl Sci,2009,32:2102-2122.
[3]Han Xiaosen,Wang M ingxin.General decay of energy for a viscoelastic equation w ith non linear dam p ing[J].M ath M eth A pp l Sci,2009,32:346-358.
[4]Liu Kangsheng,Liu Zhuangyi.On the type of C0-sem igroup associated w ith the abstract linear viscoelastic system[J].Z Angew Math Phys,1996,47(2):1-15.
[5]Liu Kangsheng,Liu Zhuangyi.Exponential decay of energy of vibrating strings w ith local viscoelasticity[J].Z Angew M ath Phys,2002,53(2):265-280.
[6]Liu Kangsheng,Liu Zhuangyi.Boundary stabilization of a nonhomogeneous beam w ith rotatory inertia at the tip[J].JCom put App lM ath,2000,114:1-10.
[7]章春国.具有局部记忆阻尼的非均质T im oshenko梁的稳定性[J].数学物理学报A辑,2012,32(1):197-206.
[8]章春国,谷尚武,姜敬华.具有Boltzmann阻尼Petrovsky系统的稳定性[J].系统科学与数学,2013,33(7):807-817.
[9]章春国,张海燕,谷尚武.一类具有局部记忆阻尼的弱耦合系统的能量衰减估计[J].数学物理学报A辑,2015,35(1):194-209.
[10]Pazy A.Sem igroups of Linear Operators and App lications to Partical D ifferential Euqations[M].New York:Sp ringer-Verlag,1983,21(1):56-78.
[11]Huang Falun.Characteristic condition for exponential stability of linear dynam ical system s in H ilbert spaces[J].Ann D iff Eqs,1985,1(1):43-56.
[12]Pruss J.On the spectrum of sem igroups[J].Trans Amer M ath Soc,1984,284(3):847-857.
[13]Adam s R A.Sobolev Spaces[M].New York:Acadam ic Press,1975.
M R Sub ject C lassification:35B40;93B05
Stab ility of the w eak ly coup led beam-string system w ith boundary feedback con trol
ZHANG Chun-guo,LIU W ei-w ei,ZHANG Hai-yan
(Dep t.of Math.,Hangzhou DianziUniv.,Hangzhou 310018,China)
This paper stud ies the w eak ly coup led beam-string system w ith boundary feedback control.First,under the app rop riate hypothesis,it is proved that the well-posedness of the system by using the theory of linear operator sem igroup.And then,it is showed that the energy of the weak ly coup led beam-string system w ith boundary feedback control is uniform exponential decay by app lying the frequence dom ain resu lt on H ilbert space.
beam-string system;linear operator sem igroup;boundary feedback control;uniform exponential decay
O231.4
A
1000-4424(2016)02-0185-09
2015-04-10
2016-01-06基金项目:国家自然科学基金(61374096;11271104)

