加权Morrey空间上分数次极大算子的双权不等式

张婷婷，刘秋菊，谢永红∗（.石家庄职业技术学院经济贸易系，河北石家庄050000；.河北师范大学数学与信息科学学院，河北石家庄05004）

加权Morrey空间上分数次极大算子的双权不等式

张婷婷1，刘秋菊2，谢永红2∗
（1.石家庄职业技术学院经济贸易系，河北石家庄050000；2.河北师范大学数学与信息科学学院，河北石家庄050024）

Ye与W ang研究了Hardy-Littlewood极大算子在加权M orrey空间的双权不等式.该文将Ye与Wang的结果拓展到分数次极大算子，此外也得到了Ap型的充分条件.

分数次极大算子；双权不等式；加权Morrey空间

1　引言

设0≤α＜n，f是Rn上的可测函数，分数次极大算子Mα定义为

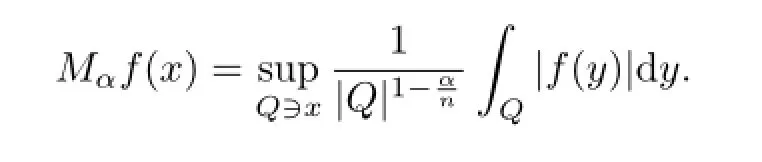
当α=0时，Mα即为Hardy-Littlewood极大算子M.

Sawyer在［1］中给出了Hardy-Littlewood极大算子以及其它正算子从Lp（ω）到Lq（u）有界的充分条件.Saw yer在［2］中得到了Mα的双权强型不等式.Cruz-U ribe在［3］中用新的方法证明了Mα的双权强型不等式.

设f是Rn上的可测函数，1＜p＜∞，0≤κ≤1，ω与u为权函数，加权Morrey空间定义为

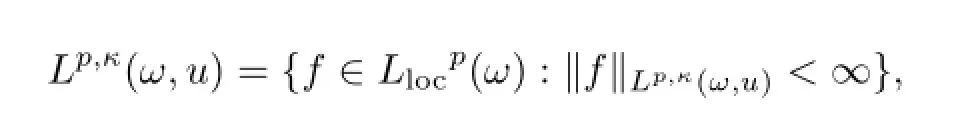
其中上确界是对于Rn上任意边平行于坐标轴的所有方体Q取的.若在上述定义中用球体B替代方体Q，得到的是同一个空间.

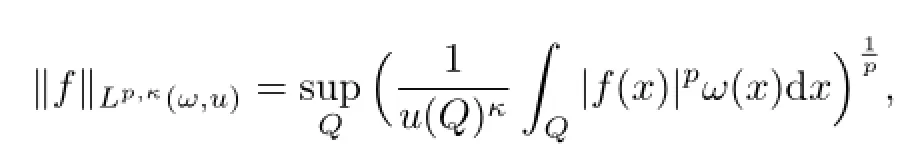
Morrey空间是由Morrey在［4］中研究二阶椭圆偏微分方程解的局部正则性时引入的函数空间，在偏微分方程解的局部正则性研究中起着重要作用.Chiarenza与Frasca在［5］中证明了Hardy-Littlewood极大算子、分数次积分算子及奇异积分算子在M orrey空间上的有界性.由于Morrey空间是Lebesgue空间的推广，因此研究各类算子在其空间上的加权有界性是自然而且有意义的.Komori与Shirai在［6］中得出了这些算子在加权Morrey空间上的有界性.关于各类积分算子在加权Morrey空间上的有界性，可参见［7-9］等文献.Ye与Wang在［10］中得到了Hardy-Littlewood极大算子在加权Morrey空间的双权不等式.

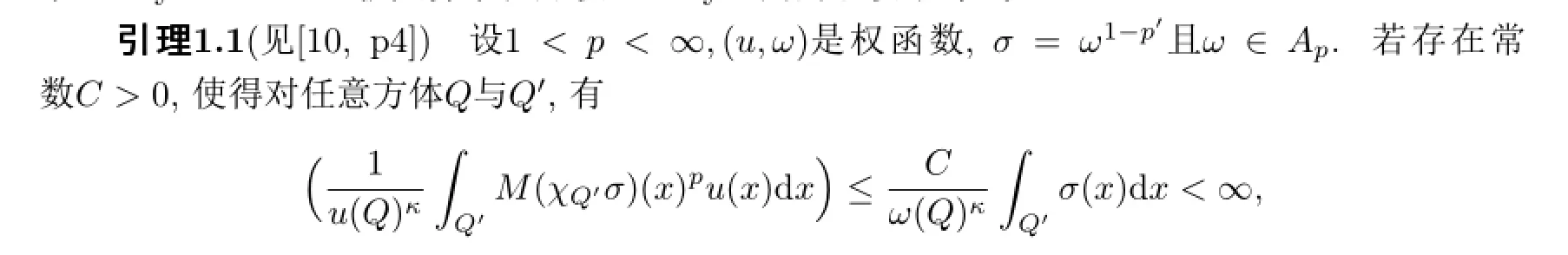
则极大算子M是从Lp，κ（ω）到Lp，κ（u）的有界算子.

本文主要讨论Morrey空间上分数次极大算子的双权不等式成立时的充分条件与必要条件，以下是本文的主要结果.

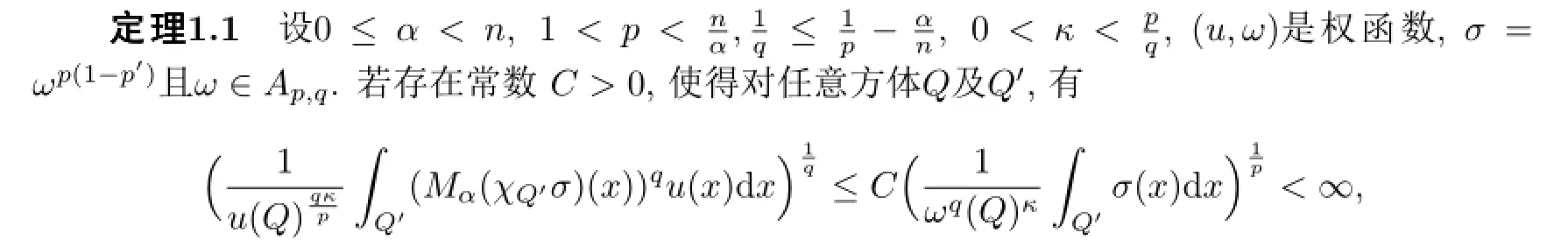
则分数次极大算子Mα是从Lp，κ（ωp，ωq）到的有界算子.

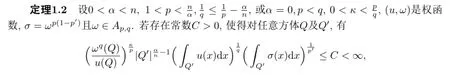
则分数次极大算子Mα是从Lp，κ（ωp，ωq）到的有界算子.

2　相关定义及引理

若ω（x）∈Lploc（R n），ω（x）≥0，a.e.x∈R n，则称ω（x）为R n上的权函数.

定义2.1（见［11，p21］）设1＜p＜∞，若

定义2.2（见［12，p261］）设1＜p，q＜∞，若

定义2.4若u是（p，q，κ）-权，ω是（p，q，κ）-特殊权，且有

则称（u，ω）∈Sp，q，κ.

引理2.1（见［11，p22］）（a）设ω∈Ap，1＜p＜∞，则ω满足二倍条件△2：对于任意方体Q，存在常数C＞0，使得ω（2Q）≤Cω（Q）；

（b）设ω∈Ap，1＜p＜∞，则ω满足拟二倍条件：对于任意ε，0＜ε＜1，存在δ，0＜δ＜1，使得对任意方体Q，有ω（εQ）≤δω（Q）.

引理2.2（见［6，p221］）若ω∈Ap，q，1＜p＜q＜∞，则

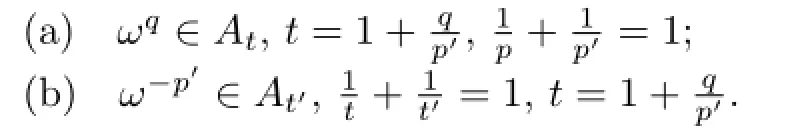
引理2.3（见［3，p36］）设0≤α＜n，f≥0是局部可积函数.若对于某个方体Q，存在t＞0，有Z

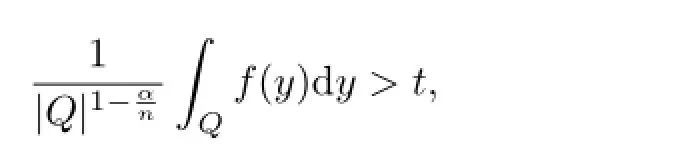
则存在二进方体P，使得Q⊂3P与

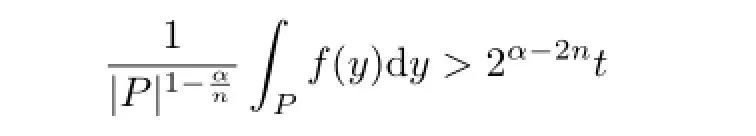
成立.

证明定理1.1，需要用到下面的引理.

可积，则下面两条等价：

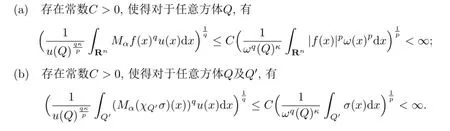
证事实上在（a）中令f=σχQ′便得到了（b）.另一方面的证明如下：首先，不失一般性，假设f∈Lp（ωp）为具有紧支集的非负有界函数，这确保了Mαf是几乎处处有限的.以下面方式分解Rn：

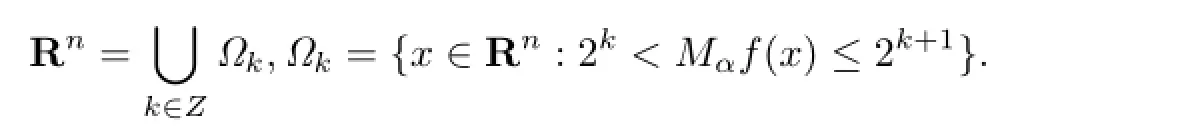
则对于每个k及任意x∈Ωk，存在包含x的方体，使得

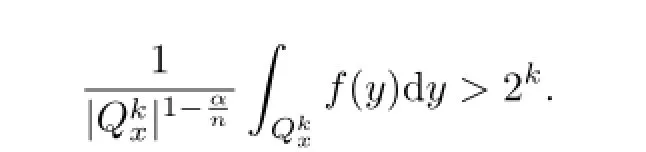
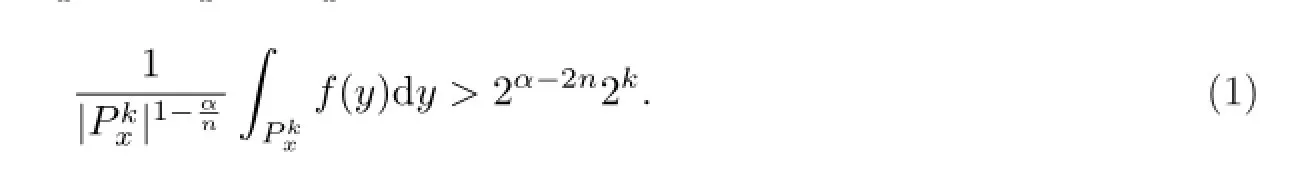
所以

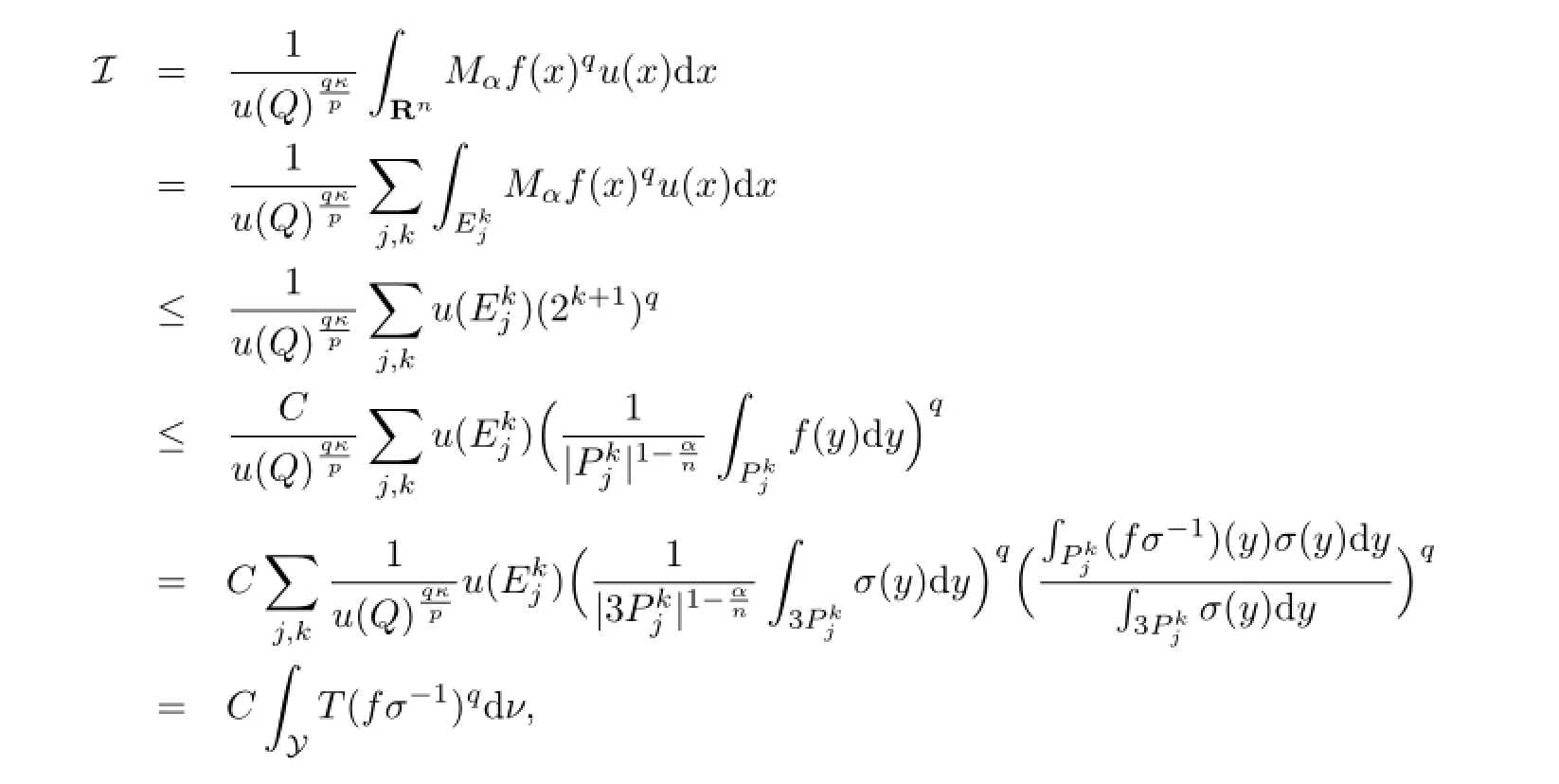
其中y=N×Z，ν是y上的测度，其定义为

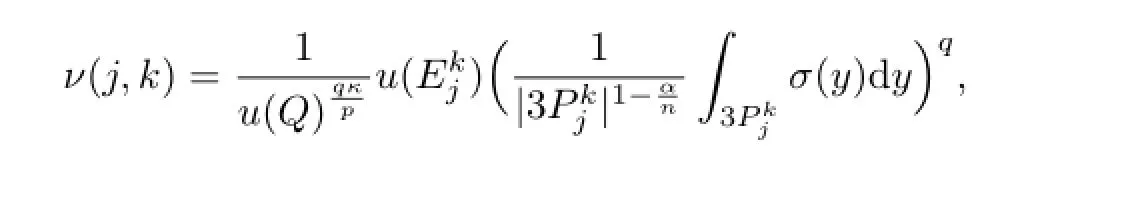
且对于每个可测函数h，算子T定义为

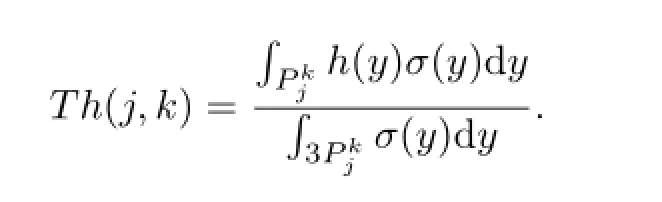
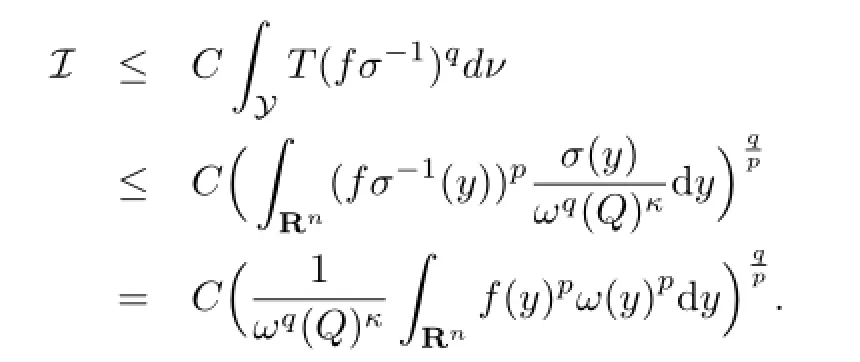
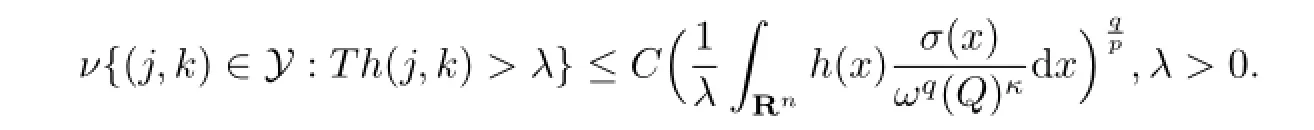
固定h≥0有界且具有紧支集，记

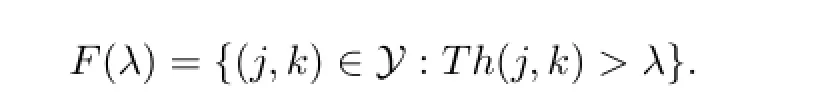
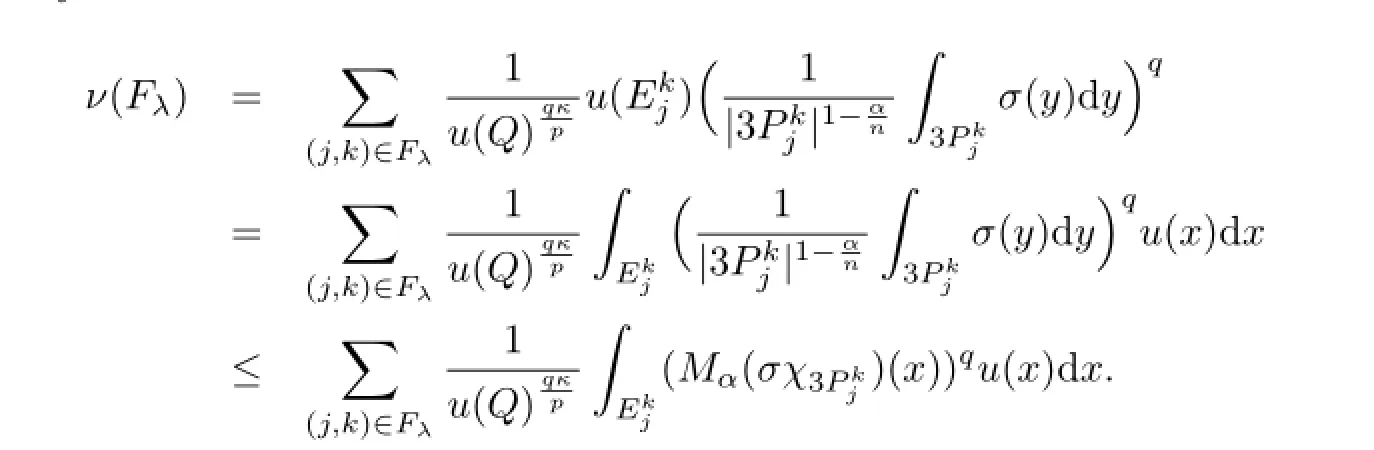
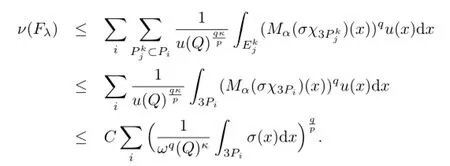
最后一个不等式应用的是条件（b）.对于每个i，由于方体Pi是从方体族中提取的，所以存在在此种情况下，有Th（j，k）＞λ，所以

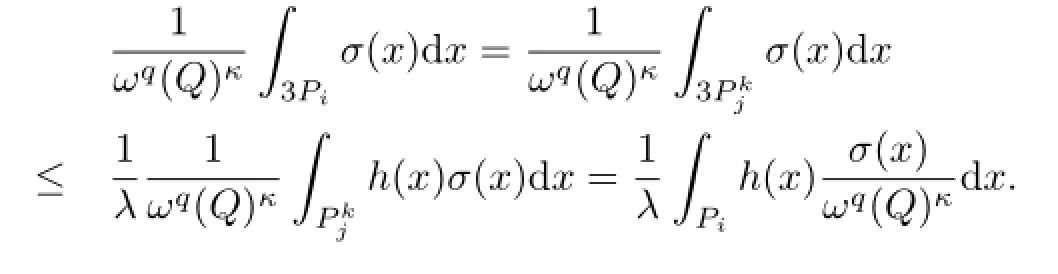
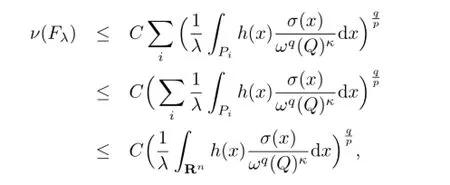
引理2.4证毕.

证明定理1.2，需要用到下面的引理.

引理2.5设0≤α＜n，1＜p＜q＜∞，0＜κ＜pq.若（u，ω）是权函数且σ=ωp（1-p′）局部可积，满足拟二倍条件，则下面两个不等式等价：

（1）存在常数C＞0，使得对于任意方体Q，有

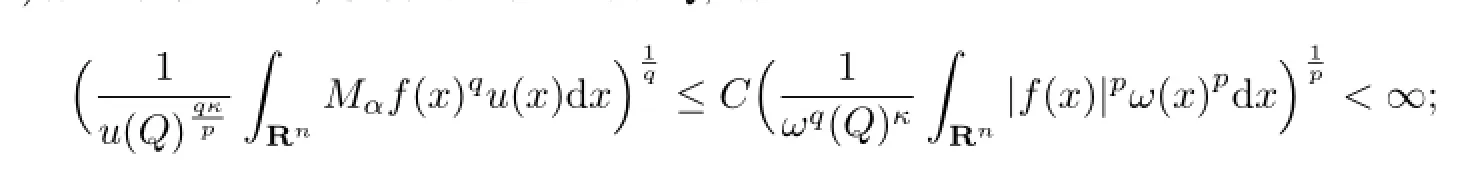
（2）存在常数C＞0，使得对于任意方体Q及Q′，有

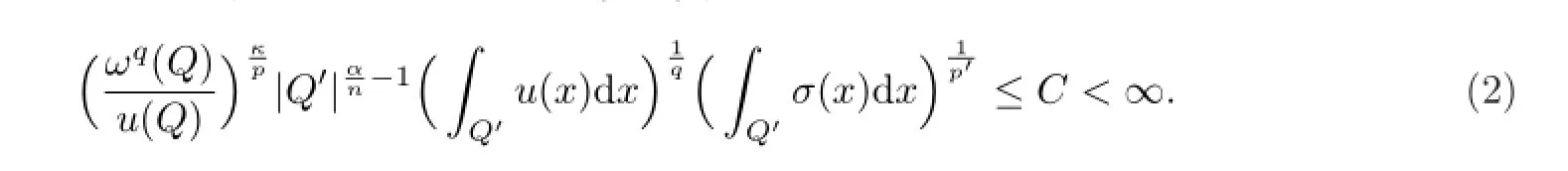
证若在（1）中取f=σχQ′，则（2）成立.（2）推出（1）的证明方法与引理2.4证明中（b）推（a）是相同的，只需要证明T是从的有界算子.利用以前相同的记号，则由不等式（2）式可得

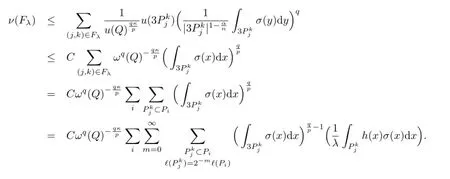
3　主要结果的证明

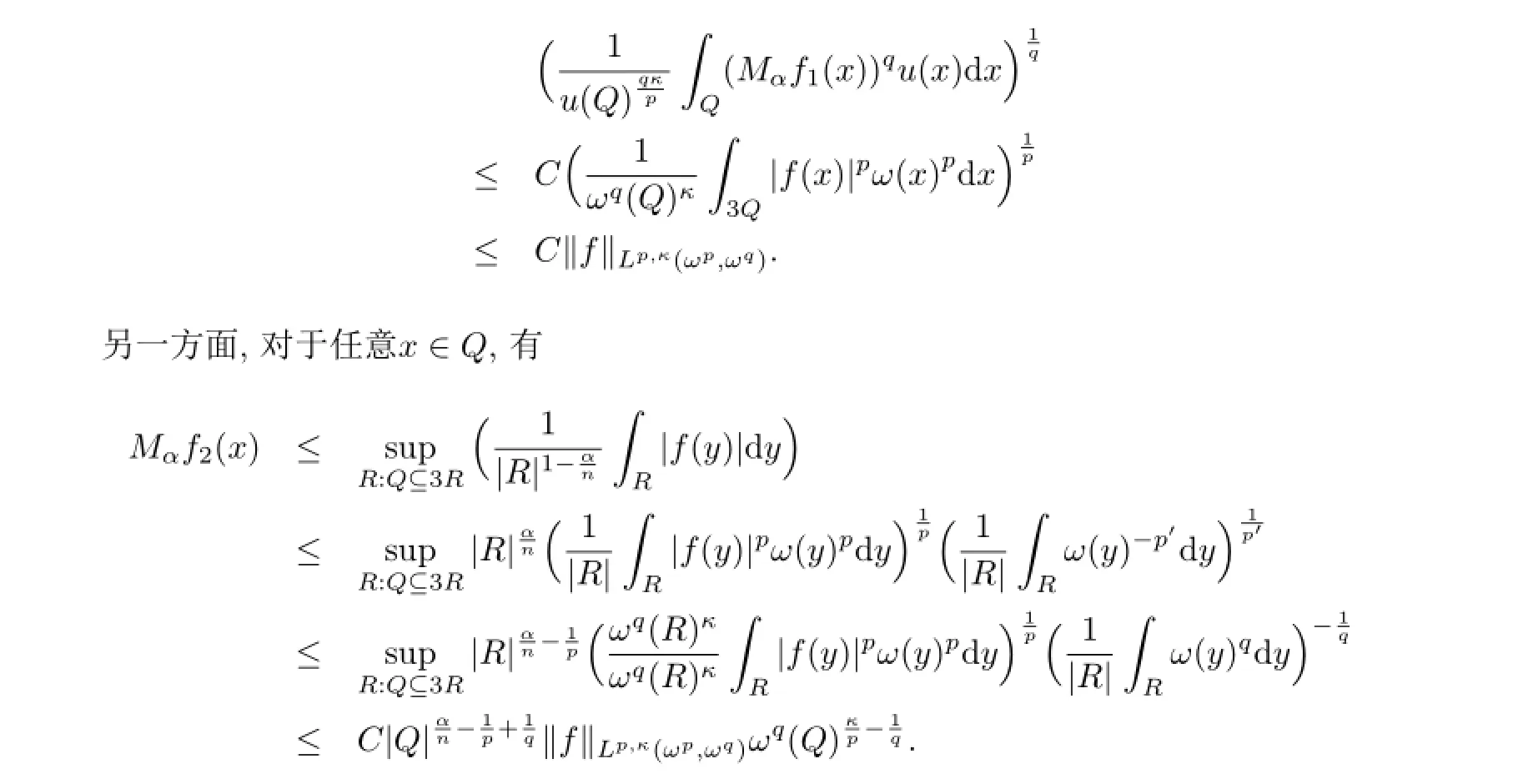
因此

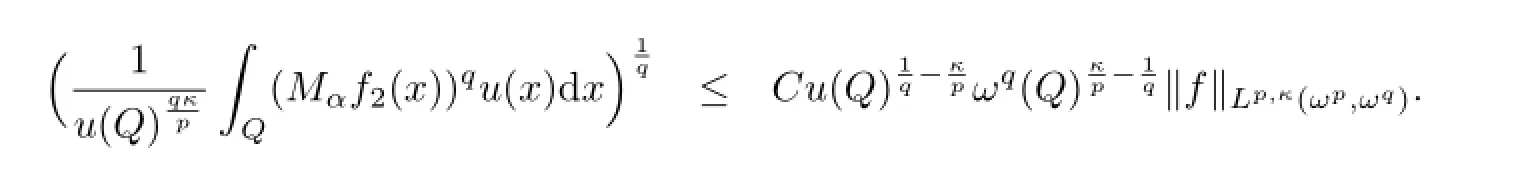
因此

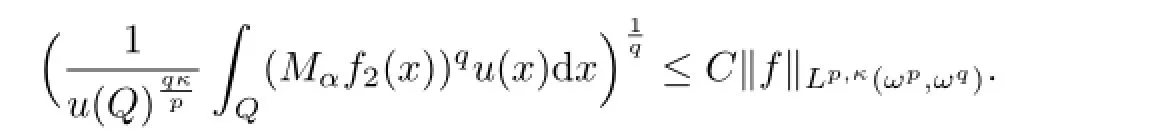
定理1.2的证明此处省略其证明，因为除了由引理2.5，引理2.1（b）与引理2.2（b）外，证明方法与定理1.1相似.

定理1.3的证明设Q1，Q2，···，Q2n是内部不相交，边长相等的相邻方体，且它们可以组成一个大的方体Q0.假设x∈Qi，i∈｛1，2，···2n｝，则对于j/=i，有

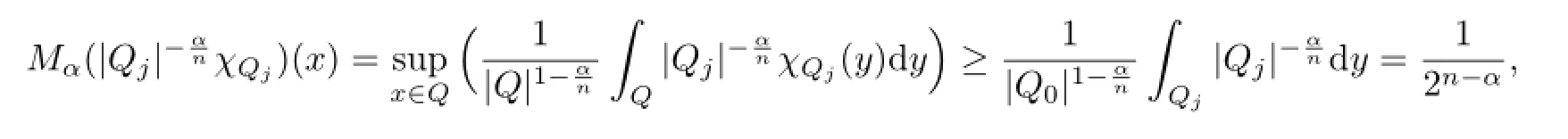
因此

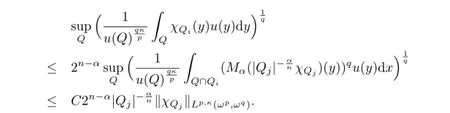
易知Qj⊆3Qi，故

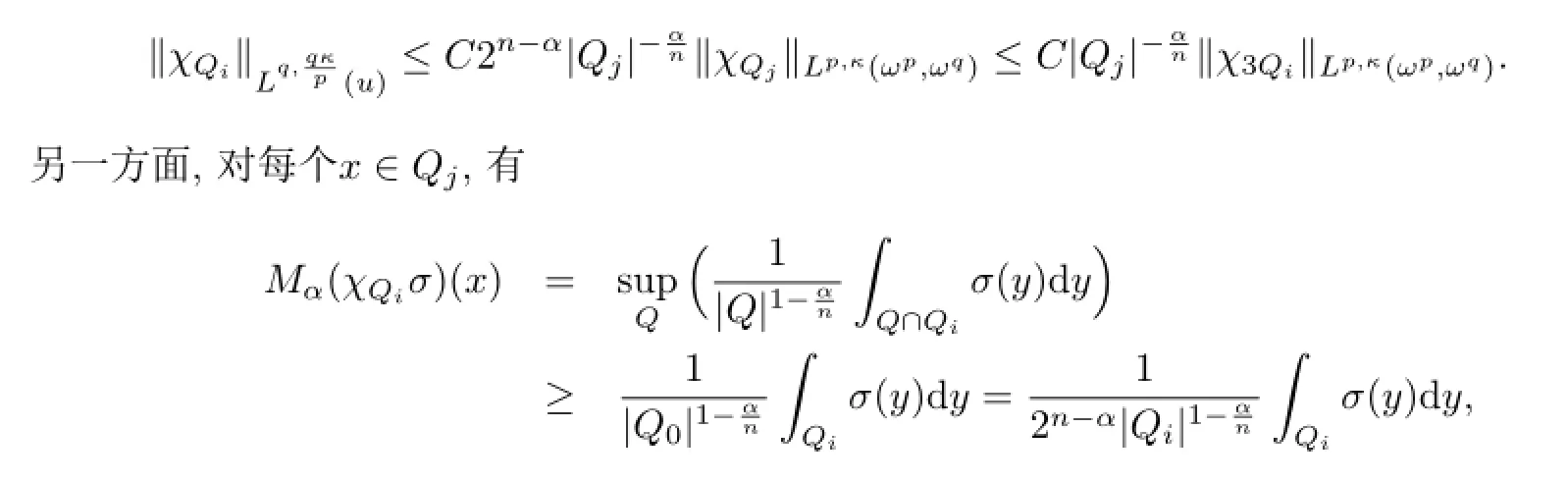
所以

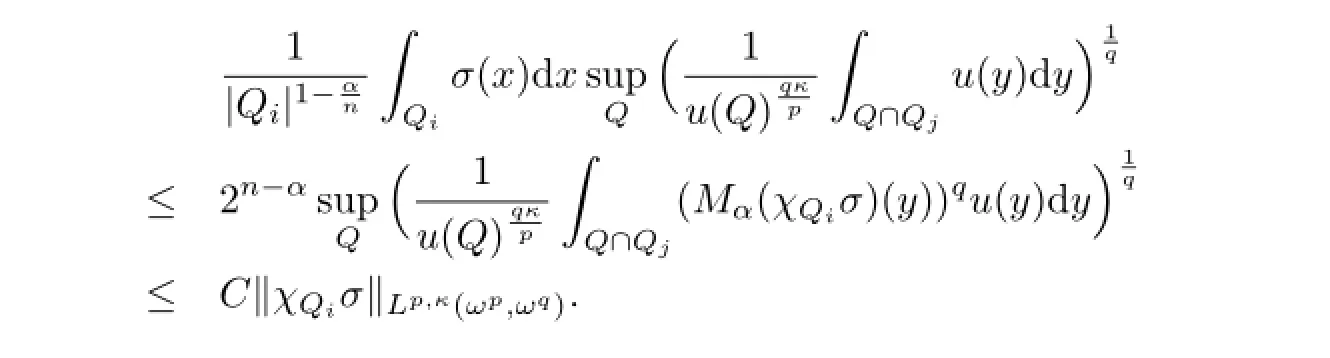
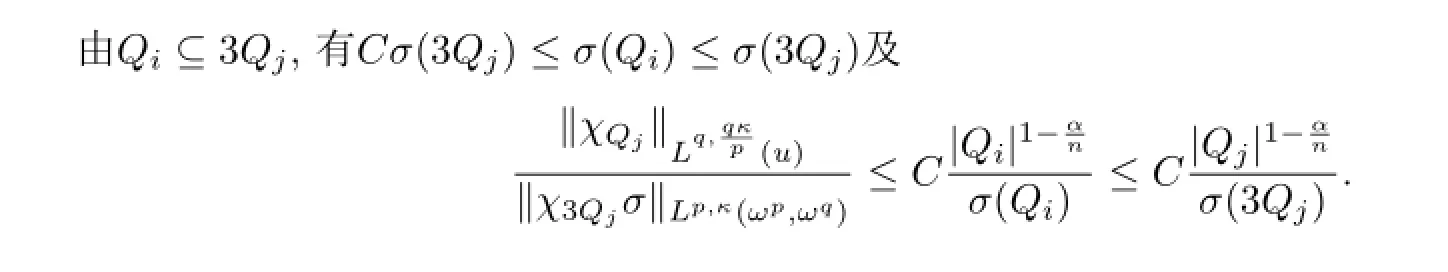
［1］Saw yer E T.Two weight norm inequalities for certain m axim al and integral operators［J］. Lect Notes Math，1982，908:102-127.

［2］Sawyer E T.A characterization of a two-weight norm inequality for maximal operators［J］. Studia M ath，1982，75（1）:1-11.

［3］Cruz-Uribe D.New p roofs of two-weight norm inequalities for the maximal operator［J］. Georgian JM ath，2000，7（1）:33-42.

［4］Morrey C B.On the solutions of quasi-linear ellip tic partial differential equations［J］.Trans Amer Math Soc，1938，43（1）:126-166.

［5］Chiarenza F，Frasca M.M orrey spaces and Hardy-Littlewood maximal function［J］.Rend Math Appl，1987，7（3）:273-279.

［6］Kom oriY，ShiraiS.W eighted M orrey spaces and a singular integraloperator［J］.M ath Nachr，2009，282（2）:219-231.

［7］Sam ko N.On a Muckenhoupt-type condition for M orrey spaces［J］.M editerr JM ath，2013，10（2）:941-951.

［8］W ang Hua.Intrinsic square functions on w eighted M orrey spaces［J］.J M ath Anal App l，2012，396（1）:302-314.

［9］Ye X iaofeng.Someestimates formultilinear commutatorson theweighted Morrey spaces［J］. M ath Sci，2012，6（1）:1-6.

［10］Ye X iaofeng，W ang Tengfei.Tw o-weighted norm inequality on weighted M orrey spaces［J］. Turk JM ath，2014，38（3）:1-10.

［11］Lu Shanzhen，Ding Yong，Yan Dunyan.Singu lar Integrals and Related Topics［M］.Hackensack，NJ，USA:W orld Scientific Pub lishing，2007.

［12］Muckenhoupt B，W heeden R L.Weighted norm inequalities for the fractional integrals［J］. Trans Amer Math Soc，1974，192:261-274.

M R Su b jec t C lassifica tion:42B 20；42B 25

Tw o-weigh t norm inequalities for fractionalm ax im al operator on weighted M orrey spaces

ZHANG Ting-ting1，LIU Qiu-ju2，XIE Yong-hong2
（1.Departm ent of Econom y and Trade，Shijiazhuang Vocational Technology Institute，Shijiazhuang 050000，China；2.College of M athem atics and In form ation Science，Hebei Norm al University，Shijiazhuang 050024，China）

The tw o-weighted norm inequalities associated w ith the Hardy-Littlewood m axim al operator on weighted Morrey spaceswere discussed by Yeand Wang.These resultsof Yeand Wangwere expanded into fractionalm axim al operator，and su fficient cond itions for Aptype were also ob tained.

fractionalmaximal operator；two-weighted inequality；weighted M orrey space

O177

A

1000-4424（2016）02-0194-09

2015-10-10

2016-04-18

国家自然科学基金（11401164；11301136；11571089；11401159）；河北省自然科学基金（A 2014205069）；浙江省自然科学基金（LY 14A 010017）；河北师范大学博士基金（L2015B04）

xyh1973@126.com