几何流方程的分离变量解

朱春蓉，储佩佩，黄守军（安徽师范大学数学计算机科学学院，安徽芜湖241000）

几何流方程的分离变量解

朱春蓉，储佩佩，黄守军
（安徽师范大学数学计算机科学学院，安徽芜湖241000）

利用不变子空间方法及拟设法，在变量变换作用下给出双曲几何流和Ricci流的各种分离变量解，包括乘法分离变量解和广义泛函分离变量解，并给出了这些解的性质分析.

几何流方程；分离变量解；不变子空间方法；拟设法

1　引言

近几十年来非线性偏微分方程出现在越来越多的领域，构造它们的精确解也变得十分重要.精确解不仅可以帮助人们理解相应问题在特殊情况下的实际意义，而且还可以辅助验证数值计算结果和相关性质分析结论，从而作为数值计算和性质分析的基础.分离变量法是构造线性偏微分方程精确解非常有效的一个方法.Fourier在研究热方程问题时发展了该方法，Sturm和Liouville在十九世纪三十年推广了这种方法.近期，这种方法无论是在概念还是在方法上都有相应的发展.

假设给定一个1+1维非线性演化方程

其中E是关于括号中变量任意光滑的函数，u是依赖于两个相互独立的自变量x和t的未知函数.如果该方程有解形如

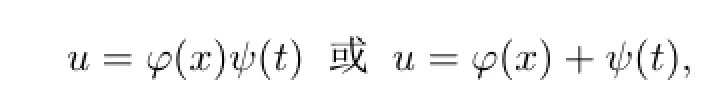
则它们被称为该方程的乘法分离变量解或加法分离变量解；如果该方程有解形如

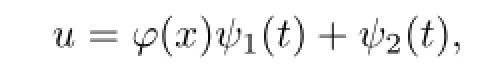
则它被称为该方程的非线性分离变量解；如果该方程有解形如

其中φi（x）（i=1，···，n）线性无关，则它称为该方程的广义分离变量解；如果该方程有解形如

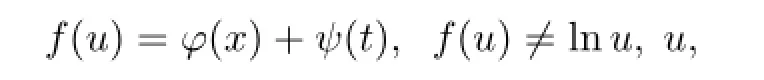
则称它为该方程的泛函分离变量解；如果该方程有解形如

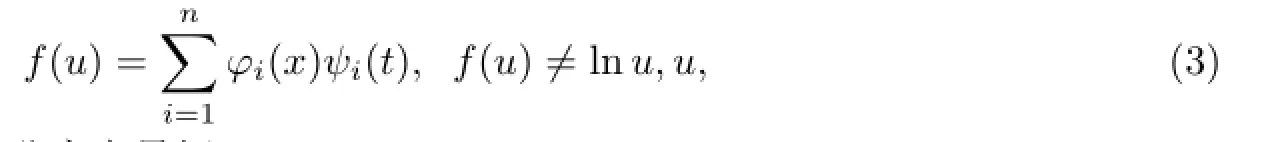
则称其为该方程的广义泛函分离变量解.

在研究偏微分方程的分离变量解时，有两个主要的问题.问题一，给定方程寻求其分离变量解；问题二，研究哪些方程具有分离变量解.围绕这两个问题的研究，上述的各种分离变量解的概念得以提出，与此同时也产生了给出这些分离变量解的方法，包括李点对称法［1］，拟设法［2-7］，广义条件对称法［8-11］，群分叶法［12-13］和不变子空间法［14-15］等.上述方法在各种不同方程及方程组中得到进一步推广和使用［16-25］.

本文讨论双曲形式几何流和Ricci流的分离变量解.为了刻画度量的波动性质，［26］提出了双曲几何流

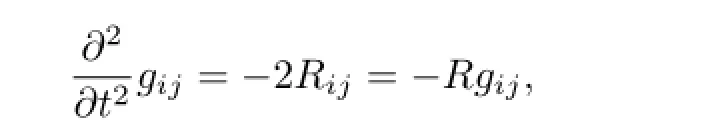
其中gij表示黎曼度量，Rij表示Ricci张量，R表示标量曲率.在黎曼曲面（M2，g）上，它可以改写为

其中u=u（x，y，t）＞0表示度量gij的共形因子，即gij=u（x，y，t）δij.Ricci流

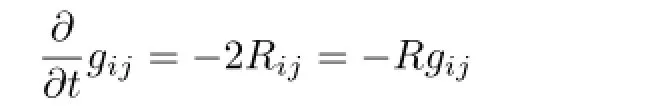
可以表示为

Ricci流是由Ham ilton于1982年在他的研究论文“Three-manifolds w ith positive Ricci curvature”中提出的［27］.众所周知，它是人们非常感兴趣的几何演化方程.在2003年左右，Perelm an应用Ricc流概念完成了Poinc´are猜想的证明［28-30］，且Ricci流和量子理论也有相关性［31］. Lie对称群是研究非线性微分方程非常有效的一种方法.Cim poiasu和Constantinescu在文献［32］中给出了二维Ricci流的对称群和群不变量.在文献［33］中，他们利用Lie对称群和优化系统的方法讨论了Ricci流的不变解.关于Ricci流的Lie对称群研究还可以参考文献［34-35］.在文献［36］中，Xu通过变量变换w=ln u给出了方程（4）和（5）的Lie对称群.在文献［37］中，Galaktionov和Svirshchevskii对这两个方程的群不变解也有研究.最近，Wang应用Xu的结果，并通过选择适当的优化系统给出了方程（4）和（5）的群不变解［38］.本文基于文献［38］，将在变量变换意义下，结合拟设法和不变子空间法考虑方程（4）和（5）的分离变量解.这里得到的解包含了文献［38］中所有的分离变量解.同时，本文还给出了很多新的分离变量解，这些解在下文中用“u∗”来表示.还对这些分离变量解的性质进行了分析，包括奇性分析和对时间的演化情况的分析.

为了便于下文的叙述，这里以非线性演化方程（1）为例，对不变子空间方法进行简单的介绍.设｛φi（x），i=1，···，n｝为一个相互线性无关的函数集合，其中n≥1.Wn表示这些函数的线性扩张，记作

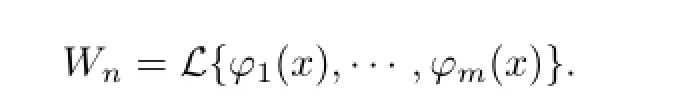
如果E［Wn］⊆Wn，那么称子空间Wn在给定算子E作用下不变，或者称算子E允许子空间Wn.在线性代数中， 这意味着

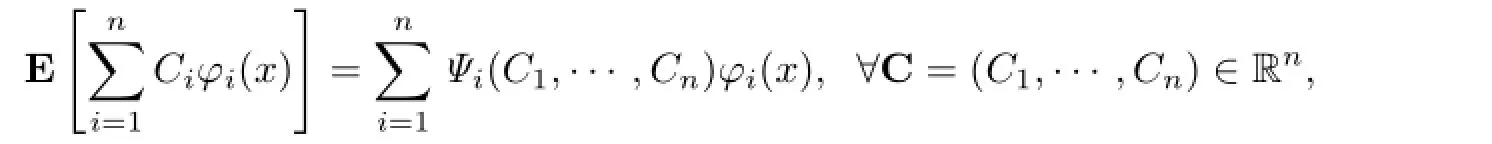
其中｛Ψi｝表示以｛φi｝作为基时E［u］在Wn中的表示系数.如果方程（1）中的非线性微分算子E允许子空间Wn，那么方程（1）具有广义分离变量解（2），其中ψi（t）（i=1，···，n）满足常微分方程组

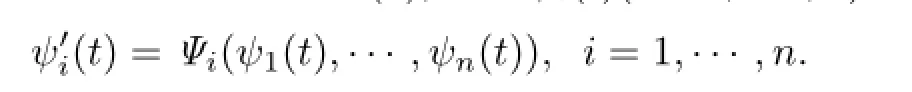
通过拟设法或者不变子空间方法理论中的不变条件可以得到非线性微分算子允许的不变子空间，具体可以参考文献［15］.

在下文中，将做如下安排：§2讨论方程（4）的分离变量解；§3讨论方程（5）的分离变量解；§4给出本文的总结和讨论.

2双曲几何流

2.1径向对称形式的解

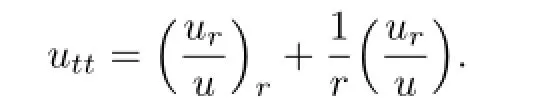
令v=ru，此方程可化为

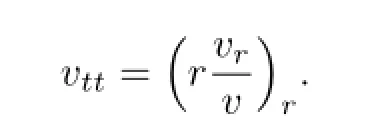
再作变换v=ωr，则有

将算子F［ω］≡ωttωr看作关于变量t的非线性微分算子，由拟设法或不变子空间理论中的不变条件可以验证它允许不变子空间代入方程（6），得到关于fi（r）（i=1，2，3）的微分方程组

由此，得到

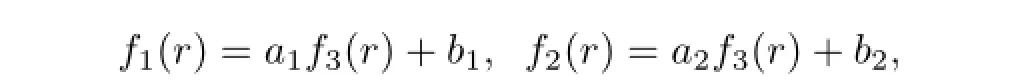
及

在这里及下文中，ai和bi均表示任意常数.求解方程（7），得到方程（4）的解

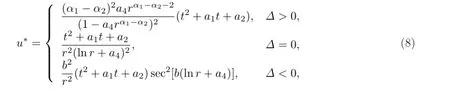
其中Δ=1-4a3.在Δ＞0情形中为代数方程0两个不相等的实根；在Δ＜0情形中

注意到，这里得到的解只会在形如｛（x，y）：x2+y2=c｝的集合上具有奇性，其中c为某个非负常数.当Δ≥0时，这样的集合至多有两个，而当Δ＜0这样的集合可能有无限多个.

2.2形如u=u（ax+by，t）的解

这里考虑方程（4）形如u=u（ax+by，t）的解，它满足方程

在此方程中，令u=ωz，则有

类似地，由拟设法或不变子空间方法知，方程（9）有解形如

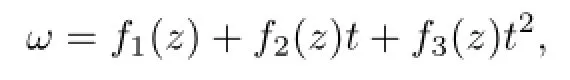
其中fi（z）满足常微分方程组

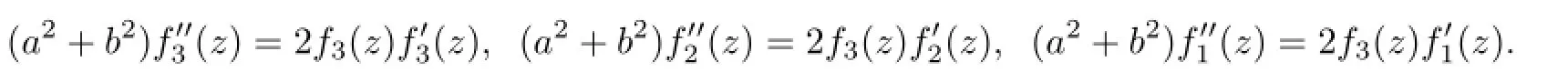
由此方程组，可以得到

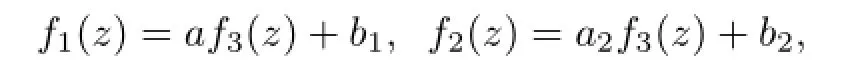
及

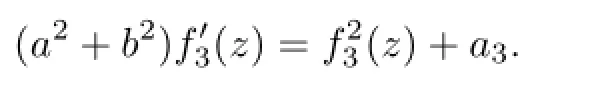
求解后，得到

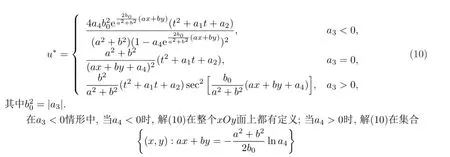
上有奇性.在a3≥0情形中，解（10）在类似的集合上也具有奇性.当a3=0时这样的集合至多只有一个，而当a3＞0时这样的集合可能有无限多个.通过2.1和2.2小节的讨论，可以看出在变量变换意义下，这两类分离变量解均依赖于关于时间t的微分算子F［ω］=ωttωr（或F［ω］=ωttωz）的不变子空间L｛1，t，t2｝给出.因此，它们具有形式

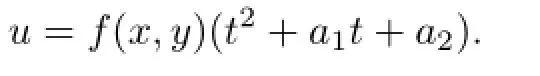
这类解为乘法分离变量解.常数ai（i=1，2）对应于u的初始状态.在解（8）中，当Δ≤0时，以及在解（10）中，当a3≥0和a3，a4＞0时，f（x，y）均是非负的，这类解每点随时间的演化如图1所示；在其它情形中，考虑到总有u＞0，解（8）和解（10）每点随时间的演化如图2所示.图中H=a21-4a2.

图1　

图2　

注1在上文中，讨论方程（4）形如u=f（ax+by，t）的解时并没有涉及方程（4）行波解的讨论，而行波解也可以看作是泛函分离变量解的一种特殊形式.因此，这里将对其进行单独讨论.在方程（4）中，令u=f（z），其中z=ax+by+ct，a2+b2/=0，c/=0.把它代入方程（4）中得到关于f（z）的二阶常微分方程

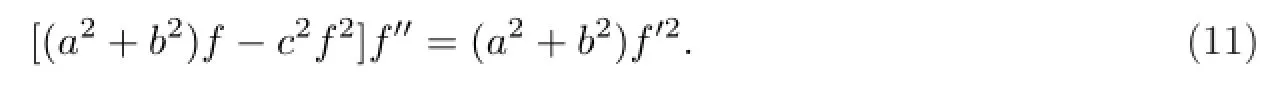
这里仅考虑方程（4）的非平凡解.在方程（11）中不显含自变量z，令f′=p，则有

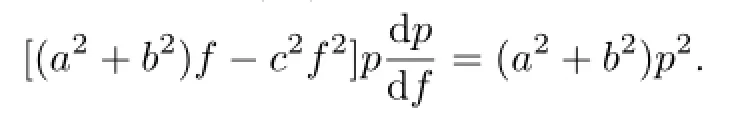
求解后，得到

其中a1为非零任意常数.由此，得到方程（4）的隐式行波解

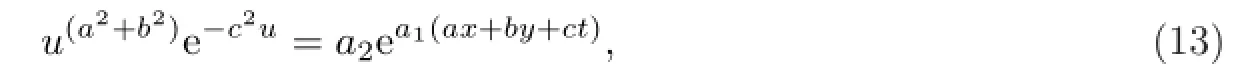
其中a2为任意正数.在文献［38］中，通过寻求群不变解也给出类似的解.本文的行波解是通过直接的方法给出，形式上更加一般.另外，利用在上述推导过程中得到的方程（11）和（12）还可以对这个隐式解的性质进行进一步分析.由方程（11）和（12）可以得到

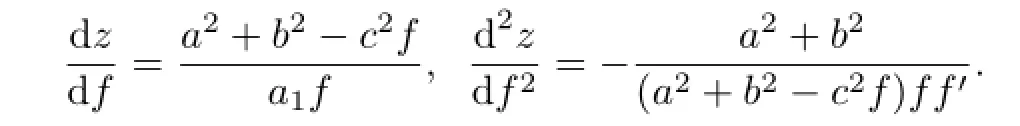
为了讨论方便，这里不妨假设a1＞0.考虑到u=f（z）＞0，通过（13）式，以及dz/d f和d2z/df2的表达式可以给出：

当a1＜0时，同理可以给出z=f-1（u）的性质分析.由上述分析，可以画出隐式解（13）两种情形下的简图，分别如图3和图4所示，其中A=（a2+b2）/c2，B=（a2+b2）［ln（（a2+b2）/c2）-1］.图3和图4中演示的为B＞0的情形，当B≤0时，也有类似的图形.

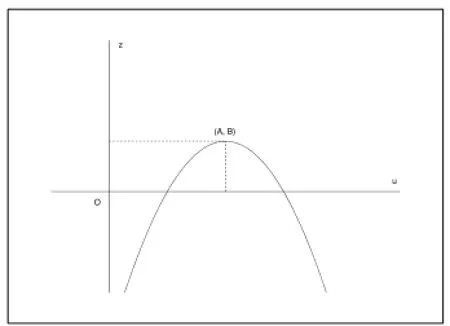
图3　（a1＞0）

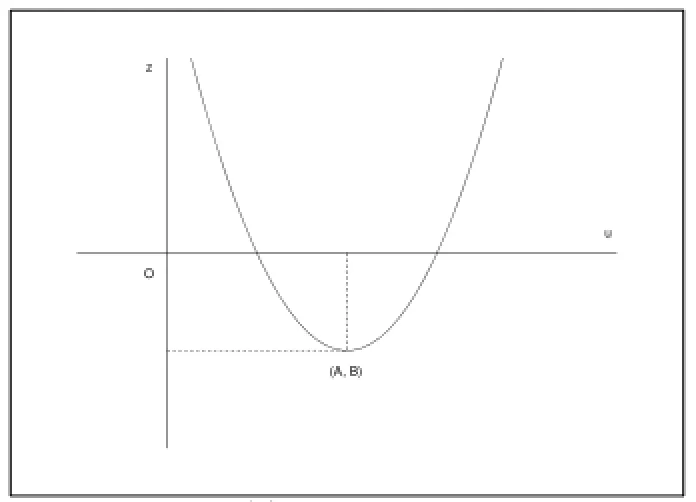
图4　（a1＜0）

3　Ricci流

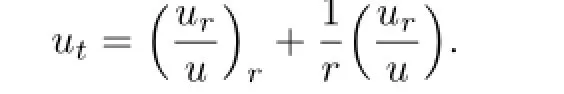
再令v=ru，则此方程转化为

在下文中，将在两种变量变换下求解此方程.

变换1 v=1/ω.

在［15］中，Galaktionov在压力变化v=un下，通过不变子空间方法给出多孔介质方程ut=（un ux）x的精确解.这里为了给出方程（14）的精确解，先作变换v=1/ω.在这种变换下，u=1/（rω），而ω满足的方程为

允许不变子空间L｛1，r，r2｝.方程（15）有解形如

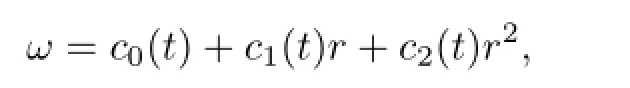
代入方程（15）后得到c0（t），c1（t），c2（t）的约束条件

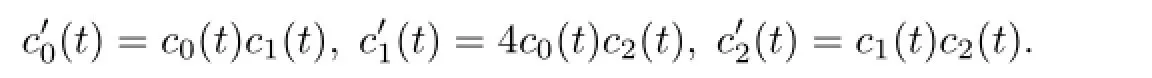
由此方程组，得到下面的关系式

求解后，得到

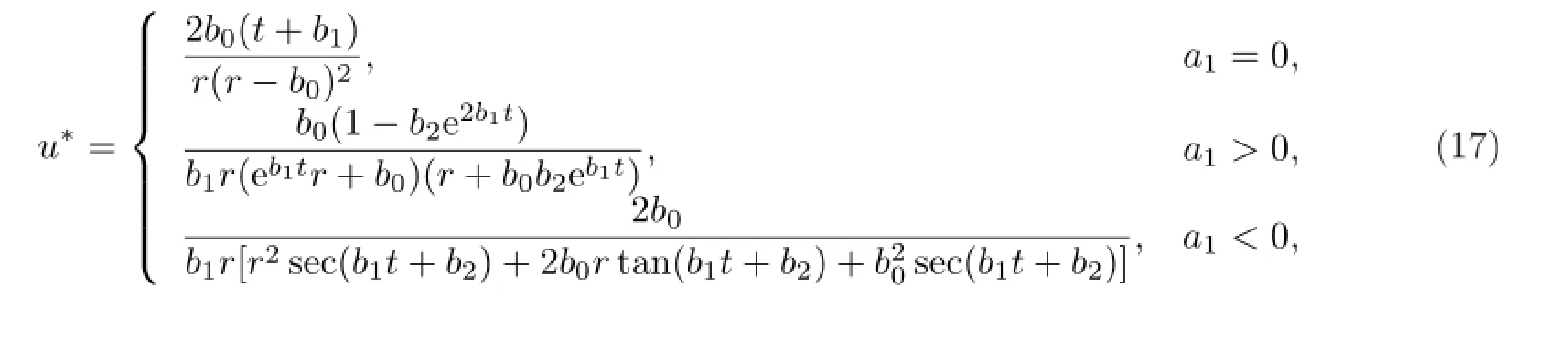
其中，在a1=0情形中解在a1=0时为乘法分离变量解；在a1/=0时，为广义泛函分离变量解.在a1=0情形中，当b0＞0时，解（17）在集合｛（x，y）：上具有奇性；在a1＜0情形中，解（17）只在（0，0）点具有奇性；在a1＞0情形中，做如下讨论.

若用（17）式构造方程（5）的解，则（17）式中常数bi（i=0，1，2）对应着解的初始状态.为了便于讨论，使用如下的记号：

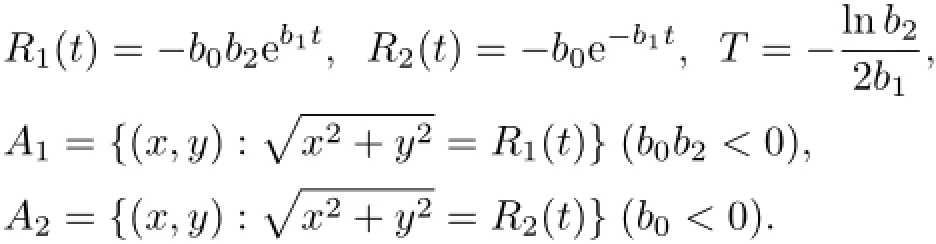
显然，当b1＞0时，

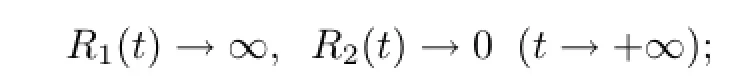
当b1＜0时，则反之.现在根据bi（i=0，1，2）的情形进行如下讨论：

（I）首先，考虑b2＜0的情形.

当b1＞0，b0＞0时，方程（5）的解在集合

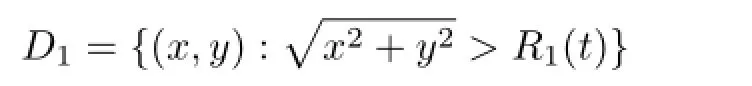
内用（17）式定义，其余点进行无穷延拓.这个解具有爆破界面A1；当b1＞0，b0＜0时，方程（5）的解在集合

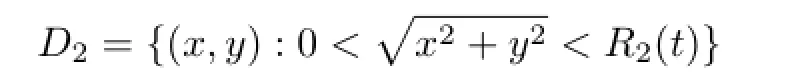
内用（17）式定义，其余点进行无穷延拓.这个解具有爆破界面A2；当b1＜0，b0＞0时，方程（5）的解在集合

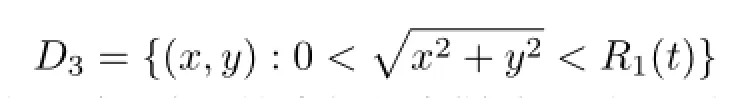
内用（17）式定义，其余点进行无穷延拓.这个解具有爆破界面A1；当b1＜0，b0＜0时，方程（5）的解在集合

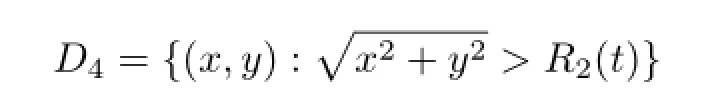
内用（17）式定义，其余点进行无穷延拓.这个解具有爆破界面A2；

（II）其次，考虑b2=0的情形.

当b1＞0，b0＞0时，用（17）式定义方程（5）的解，此解只在（0，0）具有奇性；当b1＞0，b0＜0时，方程（5）的解在集合

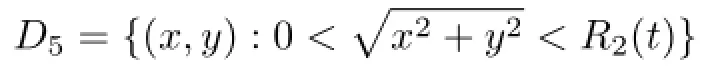
中用（17）式定义，其余点作无穷延拓.这个解具有爆破界面A2；当b1＜0时，要求b0＜0.此时，方程（5）的解在集合p

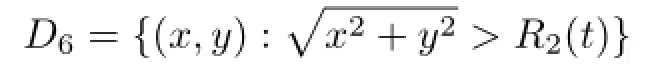
内用（14）式定义，其余点进行无穷延拓.这个解具有爆破界面A2；

（III）再次，考虑0＜b2＜1情形.若b1＞0，只在时间段［0，T）中考虑方程（5）的解.

当b1＞0，b0＞0时，用（17）式定义方程（5）的解，此解只在（0，0）具有奇性；当b1＞0，b0＜0时，方程（5）的解在集合

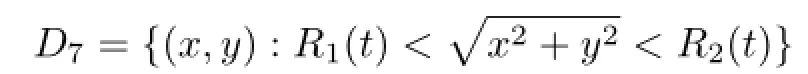
中用（17）式定义，其余点作无穷延拓.这个解具有两个爆破界面Ai（i=1，2）；当b1＜0时，要

求b0＜0.此时，方程（5）的解在集合

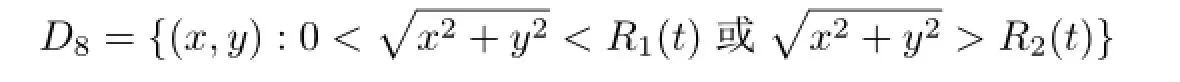
内用（17）式定义，其余点进行无穷延拓.这个解具有两个爆破界面Ai（i=1，2）；

（IV）最后，考虑b2＞1的情形.若b1＜0，只在时间段［0，T）内考虑方程（5）的解.

当b1＞0时，要求b0＜0.此时，方程（5）的解在集合

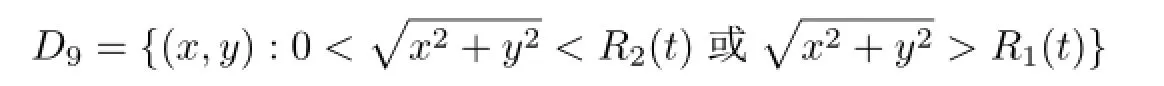
内用（17）式定义，其余点进行无穷延拓.这个解有两个爆破界面Ai（i=1，2）；当b1＜0，b0＞0时，用（17）式定义方程（5）的解，它只在（0，0）点具有奇性；当b1＜0，b0＜0时，方程（5）的解在集合

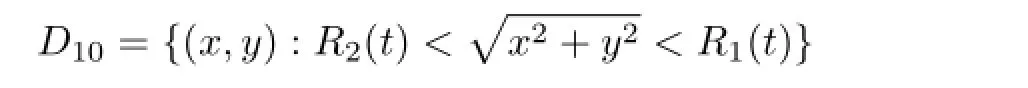
内用（17）式定义，其余点进行无穷延拓.这个解具有两个爆破界面Ai（i=1，2）.

变换2 v=ωr.

在变换v=ωr下，方程（14）变为

即

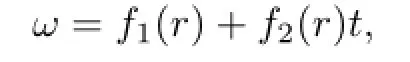
其中f1（r），f2（r）满足常微分方程组

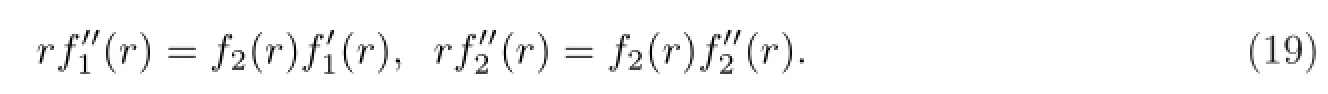
由方程组（19），有

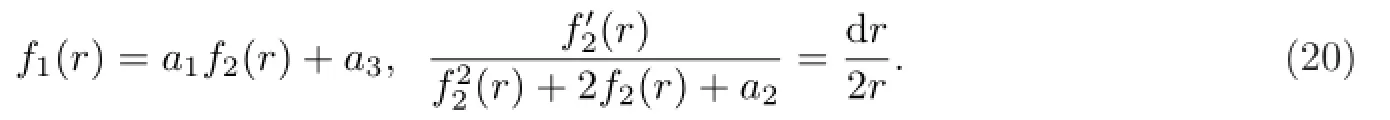
求解后，得到

其中Δ=4-4a2.在Δ＞0情形中为方程λ2+2λ+a2=0的两个根；在Δ＜0情形中，

在本小节变换2的作用下得到的解均为乘法分离变量解，且在形如｛（x，y）：的集合上具有奇性，其中c为某个非负常数.当Δ≥0时，这样的集合至多只有有限个，而当Δ＜0时这样的集合可能有无限多个.

3.4形如u=u（ax+by，t）的解

这里考虑方程（5）形如u=u（ax+by，t）的解，则方程（5）转化为

在此方程中，也采用两种变量变换进行求解.

变换1 v=1/u.

在方程（21）中，令v=1/u，有

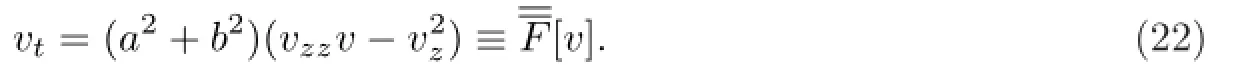
其中ci（t），（i=0，1，2）满足

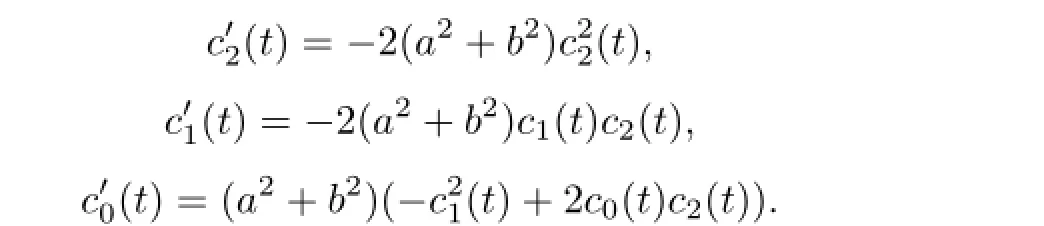
求解后，得到方程（5）的解

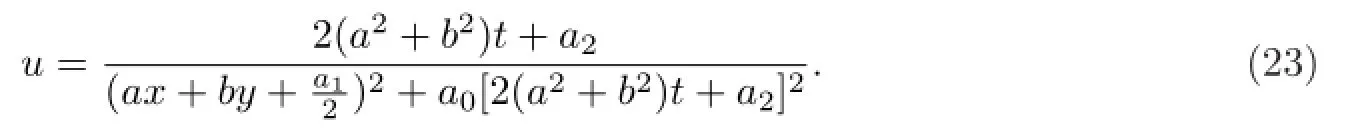
当a0/=0时，此解是广义泛函分离变量解；否则，为乘法分离变量解.

考虑到解u＞0，在（23）式中，不妨设a2＞0.当a0＞0时，由（23）式定义了方程（5）的一个整体解，且u→0（t→+∞）；当a0=0时，由（23）式定义的方程（5）的解在集合

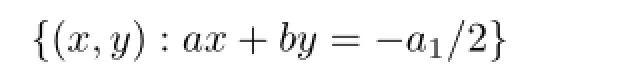
上具有奇性；当a0＜0时，不妨设a0=-c2（c＞0）.此时，在集合

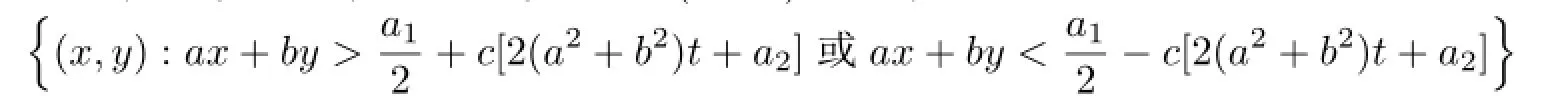
内用（20）式定义方程（5）的n解，其余点进行无穷延拓.此解有两个爆破界o面

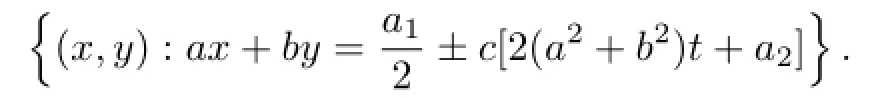
变换2 u=ωz.

在方程（21）中，令u=ωz.则它变为

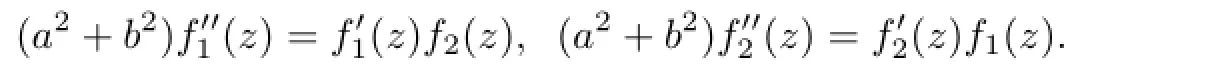
由此方程组可以给出下面的关系式f1（z）=a1f2（z）+a2，及

求解方程（24），得到方程（5）的解

在变换2作用下，得到的解均为乘法分离变量解.这些解在形如｛（x，y）：ax+by=c｝的集合上具有奇性，当a3≤0时这样的集合至多有有限个，而当a3＞0时这样的集合可能有无限多个.

注2在上文求解方程（5）形如u=f（ax+by，t）的解时，也没有涉及方程（5）行波解的讨论.这里对其行波解单独进行求解.令u=f（z），z=ax+by+ct，其中a2+b2/=0，c/=0.代入方程（5）后，有求解后，得到方程（5）的行波解

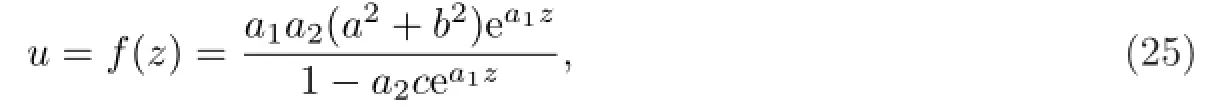
和

在（25）式中，假设c＞0.当a2＜0时，考虑到u＞0，要求a1＜0.此时，（25）式定义了方程（5）的一个整体解，且

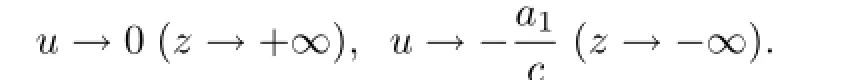
此解还是一个孤子解；当a2＞0时，在集合｛（x，y）：ax+by＜s（t）｝内可以用（25）式定义u，其余点进行无穷延拓，其中

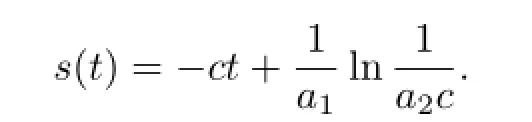
此时，解（25）具有爆破界面

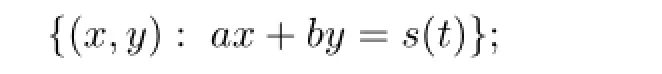
当c＜0时，可以进行类似的分析.

在（26）式中，假设c＞0.此时，在集合｛（x，y）：ax+by＜s（t）｝内用（26）式定义u，其余点进行无穷延拓，其中s（t）=-ct-（a/c）.此解具有爆破界面

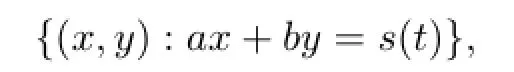
4　总结

本文从分离变量的角度，讨论了几何流方程的精确解.在求解中，这里使用了各种变量变换.在变量变换意义下，结合拟设法和不变子空间方法给出了几何流方程（4）和（5）的各种分离变量解，包括乘法分离变量解和广义泛函分离变量解.这里得到的解包含了文献［38］中应用Lie群方法给出的所有分离变量解，并给出了很多新的分离变量解.例如，方程（5）的几个广义分离变量解.还对本文得到的解在性质上进行了分析，包括奇性分析和解随时间演化情况的分析.另外，不变子空间方法是一种纯数学的方法，使用它的过程也是分析方程中涉及的非线性微分算子代数性质的过程.希望通过这种方法的使用，可以进一步明确几何流方程（4）和（5）相关的代数性质.

［1］M iller W.Symmetry and Separation of Variab les［M］.London:Cambridge University Press，1984.

［2］Galaktionov V A.On new exact blow-up solutions for nonlinear heat conduction equations［J］. Diff Int Equat，1990，3:863-874.

［3］K ing J R.Exact polynom ial solutions to some nonlinear diffusion equations［J］.Physica D，1993，64:35-65.

［4］Zhdanov R Z.Separation of variab les in the non linear wave equation［J］.J Phys A:M ath Gen，1994，27:L291-L297.

［5］Fuschych W I，Zhdanov R Z.An tireduction and exact solu tionsofnon linear heat equations［J］. JNon lin M ath Phys，1994，1:60-64.

［6］Zhdanov R Z，Revenko IV，Fushchych W I.On the new approach to variable separation in the tim e-dependent Sch r¨odinger equation w ith two space dim ensions［J］.JM ath Phys，1995，36:5506-5521.

［7］Zhdanov R Z.Separation of variab les in（1+2）-dimensional Schr¨odinger equations［J］.JM ath Phys，1997，38:1197-1217.

［8］Qu Changzheng，Zhang Shunli，Liu Ruochen.Separation of variables and exact solu tions to quasilinear diffusion equationsw ith nonlinear source［J］.Physica D，2000，144:97-123.

［9］Est´evez P G，Qu Changzheng，Zhang Shun li，et al.Separation of variables of a generalized porousm edium equation w ith non linear sou rce［J］.JM ath Anal A pp l，2002，275:44-59.

［10］Est´evez P G，Qu Changzheng，Zhang Shun li.Separation of variab les in a non linear wave equation w ith a variab le wave speed［J］.Theor M ath Phys，2002，133:1490-1497.

［11］Jia Huabing，Xu W ei，Zhao X iaoshan，et al.Separation of variables and exact solutions to non linear d iffusion equation w ith x-dependent convection and absorption［J］.J M ath Anal Appl，2008，339:982-995.

［12］Qu Changzheng，Zhang Shunli.Group foliation method and functional separation of variab les to nonlinear diffusion equations［J］.Chin Phys Lett，2005，22:1563-1566.

［13］Hu Jiayi，Qu Changzheng.Functional separab le solutions to nonlinear wave equations by group foliation method［J］.JM ath Anal App l，2007，330:298-311.

［14］Galaktionov V A.Invariant subspaces and new exp licit solutions to evolution equationsw ith quad ratic non linearities［J］.Proc Roy Soc Ed inbu rgh，1995，125:225-246.

［15］Galaktionov V A，Svirshchevskii S R.Exact solutions and invariant subspaces of nonlinear partialdifferentialequations inmechanicsand physics［M］.London:Chapman and Hall/CRC，2007.

［16］Qu Changzheng，Zhu Chun rong.C lassification of coup led system s w ith tw o-com ponent non linear diffusion equations by the invariant subspacemethod［J］.J Phys A:M ath Theor，2009，42:475201.

［17］Ji Lina.Cond itional Lie-B¨ack lund symm etries and functionally generalized separab le solutions to the generalized porusmedium equations w ith source［J］.JM ath Anal Appl，2012，389:979-988.

［18］Ji Lina.Conditional Lie-B¨acklund symmetries and invariant subspaces to nonlinear diffusion equations w ith source［J］.Physica A，2012，391:6320-6331.

［19］FengW ei，Ji Lina.Conditional Lie-B¨acklund symmetries and functional separab le solutions of generalized inhomogeneous diffusion equations［J］.Physica A，2013，392:618-627.

［20］Qu Changzheng，Ji Lina.Invariant subspaces and conditional Lie-B¨acklund symmetries of inhomogeneous non linear diffusion equations［J］.Sci China M ath，2013，56:2187-2203.

［21］Barannyk A F，Barannyk T A，Yuryk I I.Separation of variab les for non linear equations of hyperbolic and Korteweg-De Vries type［J］.Reports M ath Phys，2011，68:97-105.

［22］Barannyk A F，Barannyk T A，Yuryk I I.Generalized separation of variab les for nonlinear equation utt=F（u）uxx+aF′（u）u2x［J］.Reports Math Phys，2013，71:1-13.

［23］Ji Lina，Qu Changzheng.Conditional Lie-B¨acklund symmetries and invariant subspaces to non linear diffusion equations w ith convection and source［J］.Stud App l Math，2013，131: 266-301.

［24］Di Yanmei，Zhang Danda，Shen Shou feng，et al.Conditional Lie-B¨acklund symmetries to inhom ogeneous non linear d iffusion equations［J］.App l M ath M odel，2014，38:4409-4416.

［25］Ji Lina，Qu Changzheng，Shen Shou feng.Cond itional Lie-B¨ack lund symm etry of evolution system and app lication for reaction-diffusion system［J］.Stud App lM ath，2014，133:118-149.

［26］Kong Dexing，Liu Kefeng.Wave character ofmetrics and hyperbolic geometric flow［J］.J M ath Phys，2007，48:103508.

［27］Ham ilton R S.Th ree-m anifolds w ith positive Ricci cu rvatu re［J］.J Diff Geom，1982，17: 255-306.

［28］Perelman G.Finite extinction time for the solutions to the Ricci flow on certain threemanifolds.2003，A rxiv:0307245.

［29］Perelm an G.Ricci flow w ith su rgery on three-m anifolds.2003，A rxiv:0303109.

［30］Perelman G.The entropy formula for the Ricci flow and its geometric app lications.2002，Arxiv:0211159.

［31］Bakas I.Ricci flows and infinite dimensional algebras［J］.Fortsch Phys，2004，52:464-471.

［32］Cim poiasu R，Constantinescu R.Symmetries and invariants for the 2D-Ricci flow model［J］. JNon lin M ath Phys，2006，13:285-292.

［33］Cim poiasu R，Constantinescu R.Symmetries，integrability and exact solutions for nonlinear system s.2011，A rx iv:1111.1377.

［34］Cim poiasu R.Conservation law s and associated Lie symm etrries for the 2D Ricci flow model［J］.Rom J Phys，2013，58:519-528.

［35］Nadjafikhah M，JafariM.Symmetry reduction of the two-dimensionalRicci folw equation［J］. Geom，2013，373701.

［36］Xu Chao.Symm etries of geom etric flow s.2010，A rX iv:1001.1394.

［37］Galaktionov V A，Svirshchevskii S R.Invariant solutions of nonlinear diffusion equations w ith m axim al symm etry algebra［J］.J Nonlin M ath Phys，2011，18:107-121.

［38］W ang Jinhua.Symm etries and solu tions to geom etrical flow s［J］.Sci China M ath，2013，56: 1689-1704.

M R Su b jec t C lassifica tion:53C 44；35C 99；83C 15

Separab le solu tions of geom etric flow

ZHU Chun-rong，CHU Pei-pei，HUANG Shou-jun
（College of M athem atics and Com puter Science，Anhui Norm al University，W uhu 241000，China）

In the sense of change of variab les，separab le solutions to the geometrical flows are constructed by invariant subspacemethod and ans¨atz-based method.Product separab le solutions and generalized functional separab le solutions are included.The behavior of these solutions are described.

geometrical flows；separab le solutions；invariant subspace method；ans¨atz-based method

O175.2

A

1000-4424（2016）02-0203-12

2016-02-23

国家自然科学基金（11301007）；安徽省自然科学基金（1408085QA 05；1408085M A 01）