慢性病发病率置信区间的构造

白永昕，田茂再，2（.兰州财经大学统计学院，甘肃兰州730020；2.中国人民大学应用统计科学研究中心中国人民大学统计学院，北京00972）

慢性病发病率置信区间的构造

白永昕1，田茂再1，2
（1.兰州财经大学统计学院，甘肃兰州730020；2.中国人民大学应用统计科学研究中心中国人民大学统计学院，北京100972）

在流行病研究中，发病率是一个重要指标，该指标反映的是特定人群中某种疾病的发病程度.因此，对它的置信区间的构造在判别疾病发病程度上具有重要的医学意义.对于一些慢性疾（如癌症或心血管等），由于其发病周期长，发病率低，Poisson抽样下要比二项抽样，逆项抽样更符合事实.利用四种方法研究了泊松分布下慢性病发病率的置信区间构造，并通过Monte Carlo模拟对四种方法的表现性能进行比较.模拟结果表明：当发病率较高时，枢轴量方法无论在区间长度还是覆盖率上都表现最佳；当发病率相对较低时，枢轴量方法在区间长度上略次于Wald统计量方法和得分方法，但是在覆盖率上表现最佳.因此，枢轴量方法整体上表现的很好.

发病率；Poisson抽样；区间估计；Monte Carlo模拟

1　引言

Poisson分布是统计学中是一种常见的离散分布，用于描述单位时间内时间事件发生特定次数的概率.Poisson分布有如下的特点：（1）时间间隔很小的时，事件发生的次数很可能是0或者是1.（2）每个事件发生与否是相互独立的.（3）事件发生的概率大小与时间间隔成正比.事实上，如果潜在疾病是罕见的或者发生是随机的，则发病数在固定的一个时间间隔中服从Poisson过程.在流行病领域，一些慢性疾病（如癌症或心血管等）的发病率低，发病周期长.因此，Poisson分布被广泛使用（见［1-5］）.

在流病学中，对发病率，相对风险，风险差等参数置信区间估计的研究很多.Casella& Berger［3］基于二项，负二项，F分布之间的关系提出了逆抽样下单比例置信区间的精确估计. Lui［4］通过Wald统计量，一致最小二乘无偏估计和似然比检验三种渐近方法构造了逆抽样下风险差的置信区间.但是，在小样本的情况下，渐近方法在区间覆盖率和区间长度上存在一定的偏差.在此之下，Tang&Tian［5］提出了置信区间构造的鞍点逼近方法，并通过蒙特卡罗模拟证实：在小样本的情况下，鞍点逼近方法表现最优.2008年，田和吴［6］发表了逆抽样下发病率的渐近置信区间和逼近置信区间.随后，Tang等人对逆抽样下风险差的置信区间构造进行研究，相继发表了逆抽样下风险差的渐近置信区间和逆抽样下风险差的逼近置信区间（分别见Tang& T ian［7］和Tang&T ian［8］）.期间，吴等人［9］又提出了对逆抽样下相对差置信区间构造W ald统计量估计方法和对数Wald统计量估计方法.

同样，在二项抽样下相关参数置信区间的相关文献也很多.在Chen［10］提出了在二项抽样下风险差置信区间的两种精确估计方法.Koopman［11］和M iettinen&Nurm inen［12］先后发表了相对风险置信区间的似然比检验估计方法.之后，Gart［13］推导了得分检验估计方法，并且该方法在多数情况下表现非常好.在前人研究的基础上，钱等人［14］发表了二项抽样下相对风险置信区间估计的鞍点逼近方法.

大多数相关参数置信区间构造的研究都是基于二项抽样和逆抽样，Poisson抽样下的有关文献很少.Lui［15］中提出了Poisson抽样下发病率置信区间的Wald估计方法和基于Fisher定理的改进方法.因此，基于前人的研究，本文在Poisson抽样下分别通过Wald方法，基于Fisher定理的改进方法，枢轴量方法，得分方法，和似然比检验方法四种方法对发病率的置信区间进行估计，进而通过Monte Carlo模拟对此四种方法进行比较，以便今后进一步利用应用此结果.

本文在§2介绍了置信区间四种估计方法的原理.§3通过M onte Carlo模拟对四种方法进行比较；§4运用实例加以验证Monte Carlo的模拟结果；§5对模拟的结果进行评价.

2　置信区间

当潜在疾病是罕见时，通常假设发病人数在固定的一个时间间隔中服从Poisson过程.但是由于慢性病的发病期长，发病率低，在规定的时间间隔中观察到的发病人数很有可能为0，因此，在疾病跟进期进行n次独立重复试验.那么在整个跟进期总的发病人数X服从如下Poisson分布：

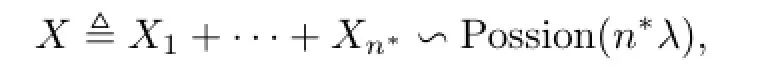
其概率密度函数为：

其中，λ表示潜在的发病率，n∗表示总的试验次数.

由矩估计方法n∗λ=X，可以得到λ和方差λ的估计值为

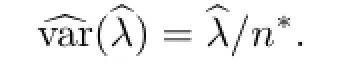
下面介绍关于发病率λ置信区间估计的四种方法.

1 Wald方法

考虑如下假设H0：λ=λ0对H1：λ/=λ0，Wald统计量为：

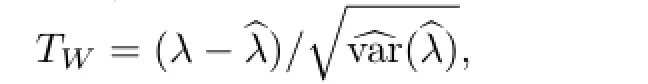
在样本量和大的情况下，Wald统计量近似的服从标准正态分布.即

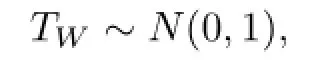
因此，可以得到λ的一个置信水平为100（1-α）%的置信区间如下

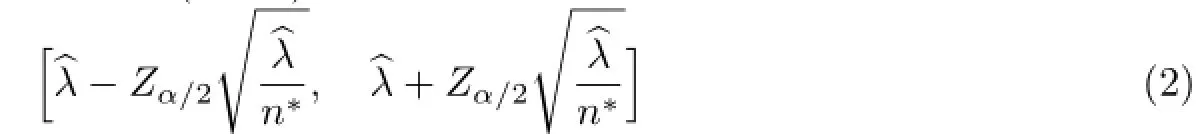
其中，Zα/2是N（0，1）分布的1-α/2分位点.

2枢轴量累积分布

引理1（见文［3］中定理9.2.14）假设T是累积分布函数为FT（t|θ）=P（T≤t|θ）的一个离散统计量，α1+α2=α（0＜α＜1）是一个固定的值.对于每个t∈Γ，θL（t）和θU（t）定义如下：

a如果对于每个t，FT（t|θ）是θ的递减函数，有

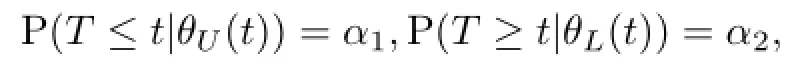
b如果对于每个t，FT（t|θ）是θ的递增函数，有

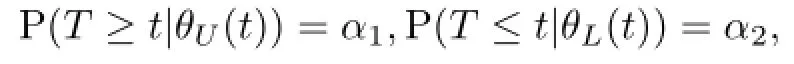
则随机区间［θL（T），θU（T）］是θ的一个置信水平为1-α的置信区间.

对于X～Poisson（n∗λ），假定α1=α2=，X=x0是观察值，由以上定理可得

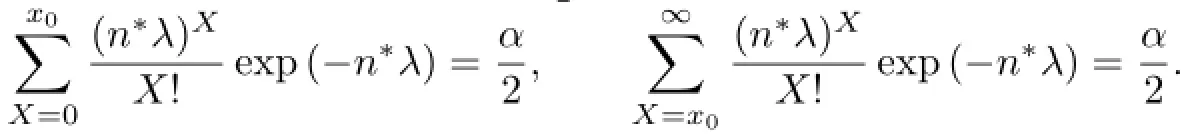
根据Γ分x布，Poisson分布以及χ分Z布 之间的特殊关系（见文［3］中例3.3.1），进一步得到

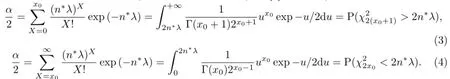
其中，χ22（x0+1），α/2是自由度为2（x0+1）的卡方分布的α/2分位点.

因此，求解方程（3）可以得到

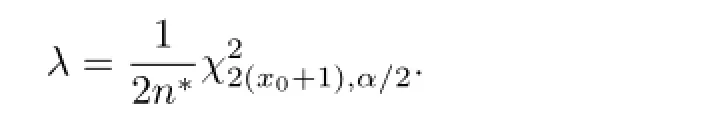
同样，求解方程（4）可以得到

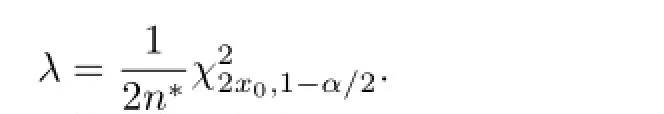
则得到λ的一个置信水平为100（1-α）%的置信区间如下

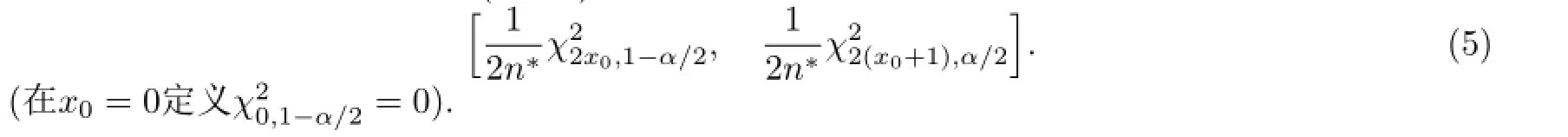
3得分检验

考虑如下假设H0：λ=λ0对H1：λ/=λ0，有

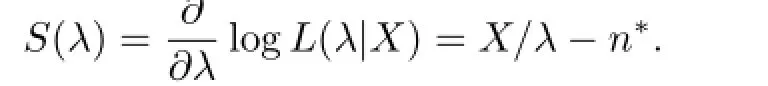
对于所有的λ都有ES（λ）=0，其方差为

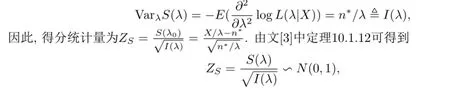
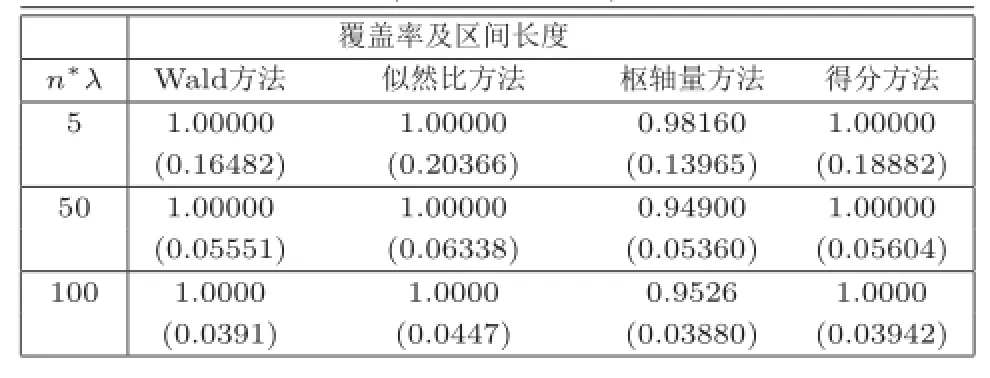
表1　Piossion分布，发病率λ=0.1，置信水平α=0.05

从而有

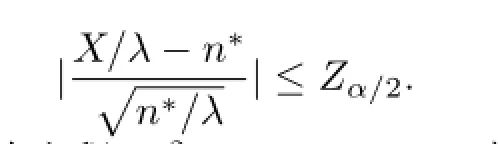
进一步转化成求解关于λ的二次方程Aλ2+Bλ+C=0，其中

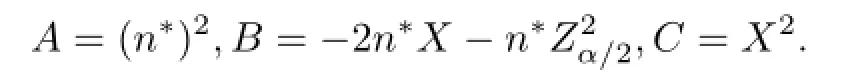
从而得到λ的一h个置信水p平 为100（1-α）%的置信区间p为 i

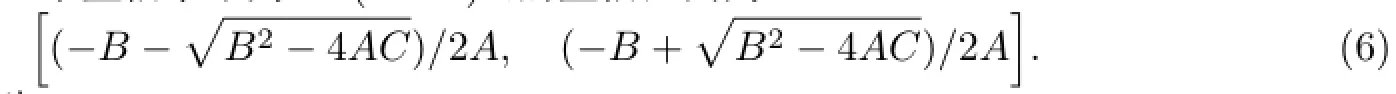
4似然比检验

似然比检验是一种构造参数检验的方法，考虑假设H0：λ∈Λ0对H1：λ∈Λ/Λ0，似然比统计量为：

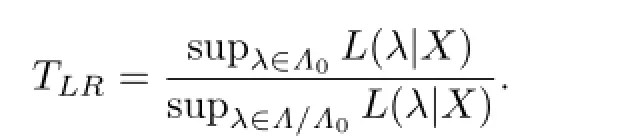
其分子分母分别是似然函数在零假设和备择假设上的最大值.

对于发病率指标，考虑如下假设检验：H0：λ=λ0对H1：λ/=λ0.根据W ilks定理，在样本量很大的时候满足

因此，可以从W的分布情况得到λ的一个置信水平为100（1-α）%的置信区间如下

3　Monte Carlo模拟

对于给出的四种置信区间，本文运用蒙特卡罗模拟从置信区间长度和覆盖率两个方面来进行比较.其中，通过参数恰好位于此区间的概率来衡量，即覆盖率越接近置信水平越好.覆盖率置信区间长度通过平均区间长度来衡量，即区间长度越短越好.

进行模拟之前，考虑如下指标：置信水平α=0.05；每次试验发病率为λ=0.001，0.01，0.1；跟进期间平均发病人数为n∗λ=5，50，100.表1，表2，表3分别是发病率λ=0.001，λ=0.01和λ= 0.1，置信水平α=0.05下不同的平均发病人数得到的模拟结果（上边的数表示覆盖率，下面的数表示置信区间长度）.

从模拟的结果来看：在发病率很低（λ=0.001）的情况下，不论平均发病人数的多少，枢轴量方法的覆盖率表现最好，其他方法均无差异.当平均发病人数很小（n∗λ=5）时，W ald统计量方法在区间长度上都表现最好，枢轴量方法较差；当平均发病人数较大（n∗λ=100）时，得分方法在0区间长度表现最好，枢轴量仅次于得分方法和Wald统计量方法.因此，在发病率很小的情况下，枢轴量方法表现出很好的优势，尤其在覆盖率上.在发病率很高（λ=0.1）的情况下，枢轴量方法无论在区间长度还是在覆盖率上都表现最好.其中，在覆盖率上除枢轴量方法的其他方法均无差异.在区间长度上，枢轴量表现最好，得分方法和Wald统计量方法次之，似然比检验方法较差.因此，枢轴量方法整体上表现良好.

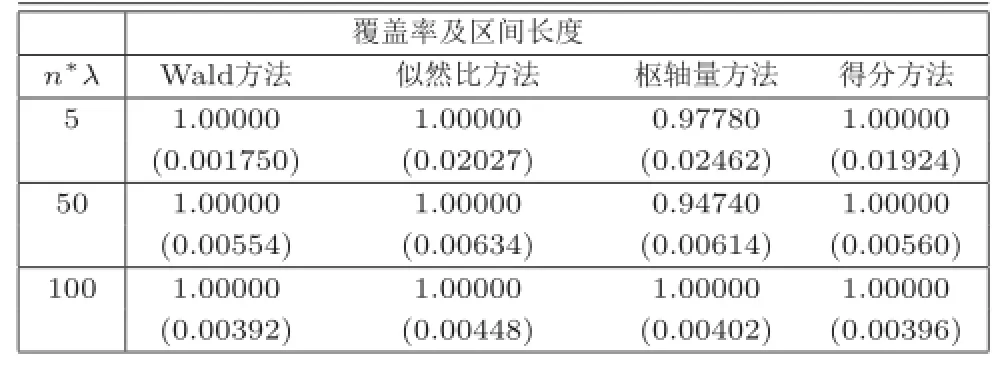
表2　Piossion分布，发病率λ=0.01，置信水平α=0.05

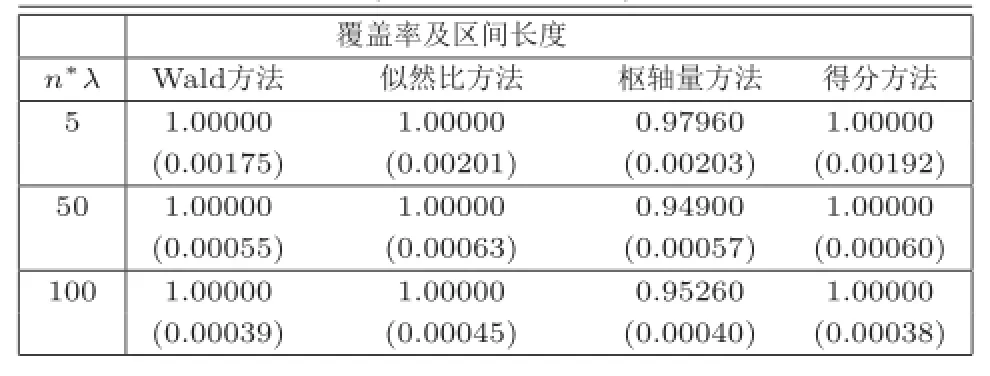
表3　P iossion分布，发病率λ=0.001，置信水平α=0.05

4　实例分析

例1患霍奇金淋巴瘤对甲状腺癌发病率的影响

霍奇金淋巴瘤（HL）是一种高度可治愈的疾病，在发病早期治愈率非常高，但在晚期会引起包括甲状腺疾病在内的各种并发症，随之引发甲状腺癌的风险也比正常人大了5-15倍.因此，文［15］对霍奇金淋巴瘤（HL）患者后来患甲状腺癌的的风险和发病特点进行研究.实验的对象是1969年到2008年之间接受治疗的1981名霍奇金淋巴瘤患者，随访时间为14.3年，期间观测到共有28个病人患甲状腺恶性肿瘤.由此可知：n∗λ=28，λ=0.014（数据来源见文［15］）.

通过上述四种方法构造的λ的95%置信区间比较见表4.

表4的结果可以看出：极大似然方法估计的区间长度明显偏大，得分方法估计的区间明显右移.相比之下，Wald方法估计的区间长度最短，枢轴量方法仅次之Wald统计量方法.

例2克罗恩病对直肠癌发病率的影响

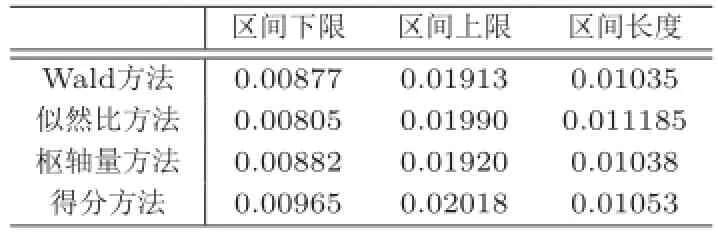
表4　患霍奇金淋巴瘤下甲状腺癌发病率的95%置信区间

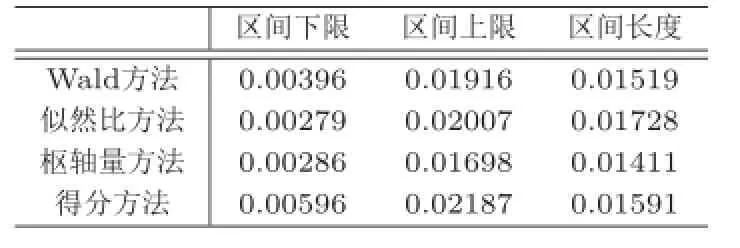
表5　感染克罗恩病的直肠癌发病率的95%置信区间

克罗恩病（CD）是一种发生在整个胃肠道的炎症，因病因不明，很难有效治疗.时间长的情况下，很可能发展成癌症.在西方国家，克罗恩患者患结直肠癌（CRC）的风险一直被认为是很高的.而在日本，关于患有克罗恩病后，肠道癌和其他所有非肠道癌的标准化发病率比（SIR）的调查却很少.文［6］研究了克罗恩疾病患者得癌症的风险.从一所专门从事炎症性肠病的医院中找出770名克罗恩疾病患者.经观察，在770个人中发现9例直肠癌（CRC）.由此可知：n∗λ=9，λ=0.0117（数据来源见文［6］）.

通过上述四种方法构造的λ的95%置信区间比较见表5.

表5的结果表明：枢轴量方法在区间长度表现最好，Wald方法次之；得分方法估计的区间整体右移且区间长度偏大；似然比方法估计的置信区间最差.

5　结论

本文通过蒙特卡罗模拟对Poisson抽样下发病率置信区间的四种估计方法进行比较，并对各种估计的性能进行评价.比较结果表明：当发病率相对较高时，枢轴量方法无论是在覆盖率还是在区间长度上都表现的非常好.当发病率较低时，枢轴量方法在区覆盖率上表现突出，在区间长度上的表现较差.因此，枢轴量方法在覆盖率和区间长度上整体表现良好.

［1］Yano Y，Matsui T，Hirai F，et al.Cancer risk in Japanese Crohn’s disease patients:investigation of the standardized incidence ratio［J］.Journal of Gastroenterology and Hepatology，2013，28:1300-1305.

［2］A liP A，W ilson J，Edge V L，et al.Community-level risk factors for notifiablegastrointestinal illness in the northwest territories，Canada，1991-2008［J］.Bm c Public Health，2013，28:1471-2458.

［3］Casella G，Berger R L.Statistical In ference［M］.California:Duxbury，2001.

［4］Kung-Jong Lui.Interval estimation on sim p le difference under independent negative binom ial sam pling［J］.Biometrics，1999，41:83-92.

［5］Tian Maozai，Tang M an-Lai，Ng H K T，et al.Con fidence intervals for the risk ratio under inverse sam p ling［J］.Statistics in M ed icine，2008，27:3301-3324.

［6］田茂再，吴喜之，李远，等.逆抽样下流行病发病率的逼近与渐近置信区间［J］.系统科学与数学，2008，26（5）:513-523.

［7］Tang M an-Lai，T ian M aozai，Ng H K T，et al.Asym p totic confidence interval construction for risk difference under inverse sam p ling［J］.Com putational Statistics and Data Analysis，2009，53:621-631.

［8］Tang M an-Lai，Tian Maozai.App roximate con fidence interval construction for risk difference under inverse sam p ling［J］.Statistics&Com puting，2010，20:87-98.

［9］吴武琴，左艳芳，李会琼，等.逆抽样条件下相对差的估计［J］.昆明理工大学学报，2009，34（5）: 108-124.

［10］Xun Chen.A quasi-exact method for the con fidence intervals of the difference of two independent binom ial p roportions in sm all sam p le cases［J］.Statistics in M edicine，2002，21: 943-956.

［11］Koopm an P A R.Con fidence lim its for the ratio of two binom ial p roportions［J］.B iom etrics，1984，40:513-517.

［12］Chan，Ivan S F，Zhang Z X.Com parative analysis of two rates［J］.Statistics in Medicine，1985，4:213-226.

［13］Gart J J.App roximate test and interval estimation of the common relative risk in the combination of 2×2 tab les［J］.Biometrika，1985，72:673-677.

［14］钱政超，张晨阳，孟令宾，等.二项抽样下基于鞍点逼近方法的流行病相对风险置信区间构造［J］.数学的实践与认识，2014，44（21）:513-523.

［15］Kung-Jong Lui.Statistical Estim ation of Epidem iological Risk［M］.New York:John W iley &Sons，2004.

［16］M ichaelson E M，Chen Yuhui，Silver B，et al.Thyroid malignancies in survivors of hodgkin lym phom a［J］.In ternational Journal of Radiation Oncology Biology Physics，2014，88（3）: 637-640.

M R Sub ject C lassification:62H 12

Con fidence in terval construction for the incidence of ch ron ic d iseases

BAIYong-xin1，TIAN Mao-zai1，2
（1.School of Statistics，Lanzhou University of Finance and Econom ics.，Lanzhou 730020，China；2.Center for App lied Statistics，School of Statistics，Renm in University of China，Beijing 100872，China）

In epidem iological studies，incidence of a disease is an im portant index which reflects the degree of the onset of a certain disease in the particu lar crowd.As a resu lt，the structure of the confidence interval of it has im portantmedical significance in judging disease extent.For some chronic diseases（such as cancer or cardiovascu lar，etc.），due to their long onset period and low incidence，Poisson sam p ling is in accord w ith the factsmore than binom ial sam p ling and inverse sam p ling.Four m ethodsw ere used to study the construction of con fidence interval for the incidence of chronic d iseases under poisson distribution，and the performance p ropertiesof the fourmethodswere com pared through m onte carlo simu lation.Simu lation results show that w hen higher incidence，p ivot m ethod did very well in both coverage and the interval length.W hen rates are relatively lower，pivotmethod is slightly in ferior to W ald statistic m ethod and them ethod of scoring on the interval length，but it d id the best on the coverage.As a resu lt，the overall performance of pivotmethod is very good.

incidence of a d iseases；Poisson sam p ling；the estim ation of confidence intervals；Monte Carlo simu lation

O212.4

A

1000-4424（2016）02-0136-07

2015-09-03

2016-05-03

教育部哲学社会科学研究重大课题攻关项目（15JZD015）；国家自然科学基金（11271368）；北京市社会科学基金重大项目（15ZDA 17）；教育部高等学校博士学科点专项科研基金（20130004110007）；国家社会科学基金重点项目（13AZD 064）；教育部人文社会科学重点研究基地重大项目（15JJD 910001）；中国人民大学科学研究基金（中央高校基本科研业务费专项资金资助）项目成果（15XNL008）；兰州财经大学“飞天学者特聘计划