非线性结构向量自回归因果图的广义似然比辨识方法
魏岳嵩(淮北师范大学数学科学学院,安徽淮北235000;西北工业大学应用数学系,陕西西安710072)
非线性结构向量自回归因果图的广义似然比辨识方法
魏岳嵩
(淮北师范大学数学科学学院,安徽淮北235000;西北工业大学应用数学系,陕西西安710072)
利用图模型方法研究非线性结构向量自回归模型的因果性问题.构建了非线性结构向量自回归因果图模型,提出图模型因果性的广义似然比辨识方法.构造同期因果关系和滞后因果关系的广义似然比统计量,使用bootstrap方法来确定检验统计量的原分布,模拟研究论述了方法的有效性.
非线性结构向量自回归模型;因果图;条件独立;广义似然比;bootstrap方法
O211.6
1 引言
检验和识别变量间的因果关系是时间序列分析的重要问题之一.近年来,图模型方法已经成为分析和处理时间序列问题的有力工具[1-3].利用搜索算法特别是PC算法分析变量间的因果关系已经成为当前常用的方法[4-6].然而利用此类方法分析因果关系存在两个主要问题,即要求时间序列模型是线性的且噪声项服从高斯分布.虽然线性及高斯性假设能使问题简单化,但研究表明非线性及非高斯性可能会更贴合实际的数据生成过程.
对于非线性时间序列的图模型问题,虽然Chu和G lym our[7]以及W ei和T ian[8]等分别利用可加模型回归法和信息论的方法获得一些有益的结论,但当前,建立有效的非线性时间序列因果关系的图模型方法仍是尚未解决的问题.本文主要讨论如何利用图模型方法来研究非线性结构向量自回归模型的因果性问题.
2 非线性结构向量自回归因果图模型
设V是一非空有限集,图G=(V,E)是一有序集,其中V中的元素称为图的顶点,而E={(a,b)|a,b∈V}中的元素称为边.若有序对(a,b)∈E而(b,a)/∈E,则称顶点a和b之间存在由a到b的有向边,记为a→b,此时称a为b的父亲(parent),a的父亲集表示为pa(a).长度为n的从a到b的路径是指由不同顶点组成的从a到b的序列{a=i0,···,in=b},满足对所有的k= 1,···,n,都有(ik-1,ik)∈E.如果对于所有的k=1,···,n,都有(ik-1,ik)∈E但(ik,ik-1)/∈E,则称该路径为有向路径.若在图G中存在由a到b的有向路径,则称b是a的后代.a的所有后代组成的集合称为a的后代集,记为de(a).
设n维时间序列{X(t)=(X1,t,···,Xn,t)T,-∞<t<∞}由p阶非线性结构向量自回归模型(Non linear Structu ral Vector Au toregressive M odels,简记为NSVAR)生成,即
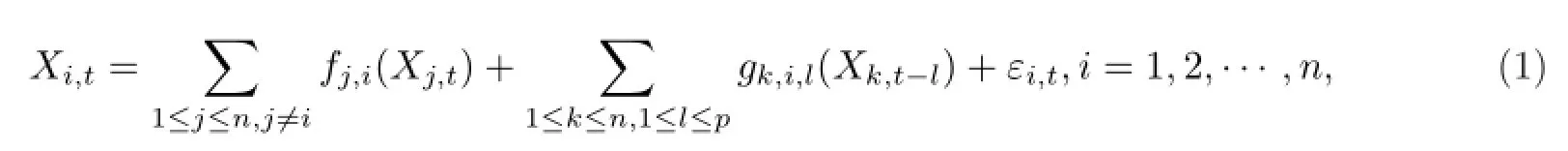
其中εit,i=1,2···n是相互独立的噪声项,fj,i(·)和gk,i,l(·)都是一元光滑函数(可以是非线性的),且不存在序列j1,j2,···,jm(m≤n)使得fj1j2,fj2j3,···,fjm-1jm,fjmj1都不为零,存在k和i使得gk,i,p(·)/=0.
NSVAR模型可以利用因果关系加以描述,即在模型(1)中,若fj,i(·)/=0,则称Xj,t是Xi,t的直接原因,并称Xj,t和Xi,t之间存在同期因果关系;若gk,i,l(·)/=0,则称Xk,t-l是Xi,t的直接原因,并称Xk,t-l和Xi,t之间存在滞后因果关系.此外,由于同期变量间不存在反馈关系,因此该模型能用有向非循环图加以解释.
定义2.1(非线性结构向量自回归因果图)对于p阶NSVAR模型(1),记

称有向非循环图G=(V,E)为非线性结构向量自回归因果图(Non linear Structu ral Vector Autoregressive Model Causal G raphs,简记为NSVARCG),如果图G满足:
定义2.2(因果M arkov条件)对于p阶NSVAR模型(1),记V={X1t,···,Xnt,X1,t-1,···,Xn,t-1,···,X1,t-p,···,Xn,t-p},有向非循环图G=(V,E)是NSVAR模型(1)的因果图,则图G满足因果M arkov条件,即对V的任意子集A总有A⊥V(de(A)∪pa(A))|pa(A),其中符号⊥表示独立,pa(A)及de(A)分别表示不包含集合A中元素的那些A中元素的父亲集和后代集合:pa(A)=∪i∈Apa(i)A,de(A)=∪i∈Ade(i)A.
3 同期因果关系的广义似然比辨识法
定理3.1设图G是模型(1)的因果图,Xt=(X1t,···,Xnt)T,Xit和Xjt是Xt的任意两元素,诱导得到的G的子图,则Xit和Xjt在G中被Xct和Xld-分离当且仅当Xit和Xjt在G1中被Xctd-分离.
证设Xit和Xjt在G中被Xct和Xld-分离,则若π是G中Xit和Xjt之间的一条仅包含Xt中点的路径,π一定是阻塞路径,因此G1中Xit和Xjt之间的任意路径都是阻塞路径,即Xit和Xjt在G1中被Xctd-分离.反之,当Xit和Xjt在G1中被Xctd-分离,则如果π是G中一条Xit和Xjt之间的相对于Xct的d-连通路径,π一定包含Xl中的点.由于不存在由Xt中点指向Xl中点的有向边,因此π中属于Xl的点都为非对冲点,从而该路径相对于Xct和Xl是阻塞的,故Xit和Xjt在G中被Xct和Xld-分离.
注定理说明当前变量之间的因果关系不受滞后变量的影响,因此在研究当前变量之间的因果关系时,分离集只需考虑当前变量集合的子集,而无需考虑滞后变量的影响,由此缩小了分离集的研究范围,降低模型结构辨识的难度.
设在NSVARCG图中,Xit和Xjt是任意两个同期变量,由于同期变量之间不存在反馈关系,若二者存在因果关系则必为Xit→Xjt或者Xjt→Xit,分别对应于两个假设:

因此,可以将确定Xit和Xjt之间的因果性方向转化为上述的假设检验问题.这是一个非参数模型对非参数模型的检验问题.这里采用Fan等[9]提出的广义似然比(Generalized likelihood ratio,简记为GLR)方法处理上述的假设检验问题.为此,首先考虑如下两个简单的假设检验问题:
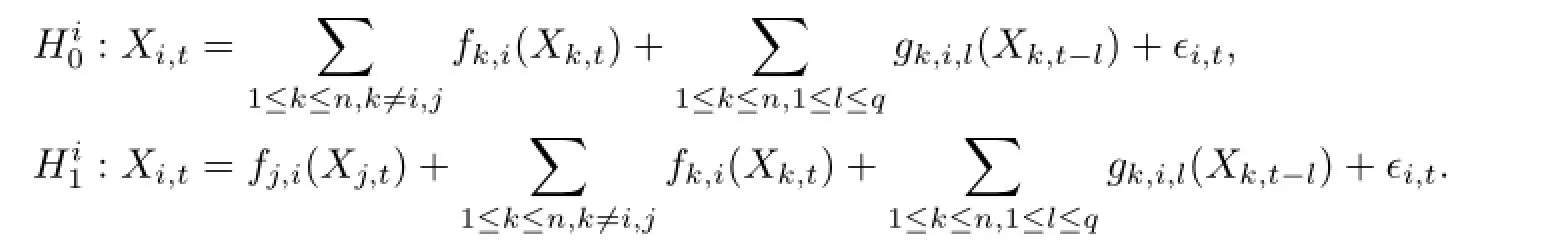
和
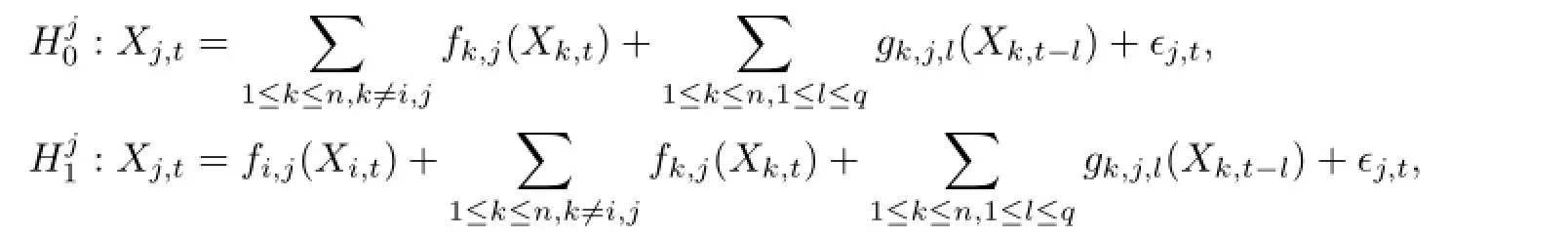

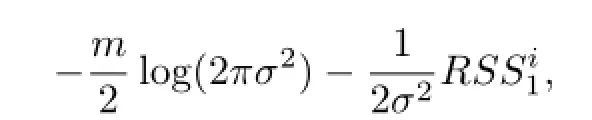
其中

将上式关于参数σ2最大化可得备择假设下的似然:

同理可得到在原假设下的对数似然为:

其中

由此可定义GLR统计量为:


从而对于同期变量因果关系定向的假设检验问题H0↔H1,构造GLR统计量:
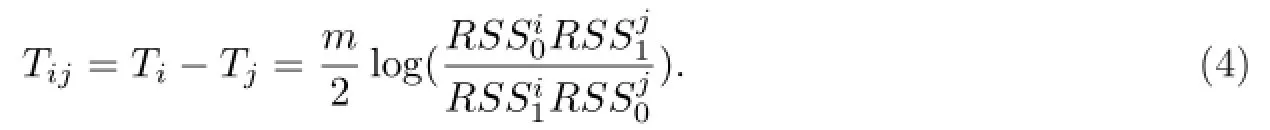
为了避免复杂的渐近方差的计算,这里利用条件bootstrap方法来计算GLR统计量Tij的p值,具体步骤如下:
步骤2计算GLR检验统计量Tl,Tij及备择模型下的残差项
步骤3对于原始数据Xk,用中心化的残差序列{来生成其中是的平均值.
步骤4用这组条件bootstrap样本来构造GLR统计量和;
步骤6利用经验分布

4 滞后因果关系的广义似然比辨识法
采取和上节相同的方法,构造GLR统计量:

其中

这里同样采用条件条件bootstrap方法来计算统计量T的p值.检验步骤如下:
步骤1由局部多项式估计法拟合原假设H0和备择假设H1下的方程模型;
步骤2计算GLR检验统计量T及备择模型下的残差项εˆki,k=1,2,···,m;
步骤3对于原始数据Xk,用中心化的残差序列来生成构造条件bootsrap样其中f˜和是在步骤1中原假设下所估计的回归函数;
步骤4用这组条件bootstrap样本来构造GLR统计量;
步骤6利用经验分布

作为T在原假设下分布的近似分布.对选择的显著性水平α,构造拒绝域(-∞)和(C1-,+∞),其中Cα表示分布B(x)的α分位点;
5 模拟分析
为了验证所给方法的有效性,对以下三个模型进行数值模拟,三个模型分别选取为线性结构向量自回归模型、非线性可加模型和非线性结构向量自回归模型.同时为了加以比较,也分别利用PC算法、文[7]提出的可加自回归方法(简记为ARM方法)以及文[8]提出的信息论方法(简记为ITM方法)对所给模型做模拟分析.
模型1:

模型2:

模型3:

其中εit~N(0,1),i=1,2,3是相互独立的噪声项.
对于每一个因果模型,生成样本容量为1000的模拟序列,并分别利用ITM方法,GLR方法,PC算法和ARM方法辨识原模型的因果结构.为了研究方便,所有的滞后阶数选取为2,其中在应用ITM方法时,带宽选取∈=1.0(带宽选择具体参见文[8]).在应用GLR方法时,分别采取局部多项式估计法和局部线性估计法构造GLR统计量.由于高维空间中局部数据的稀疏性,因此局部多项式估计时采用局部二次多项式拟合方法确定GRL统计量,条件bootstrap方法中B=99,显著性水平α=0.1,实验运行1000次.表1至表9给出了所得模拟结果,其中同期因果关系表中符号(以(Xt,Yt)为例)◦◦表示Xt和Yt之间不存在边,◦-◦表示Xt和Yt之间存在边但无法定向,◦→◦和◦←◦分别表示因果关系Xt→Yt和Xt←Yt.

表1 G LR算法所得模型同期因果关系比率

表2 ITM算法所得模型同期因果关系比率

表3 PC算法所得模型同期因果关系p值

表4 ARM算法所得模型同期因果关系比率

表5 ITM算法所得模型滞后因果关系比率
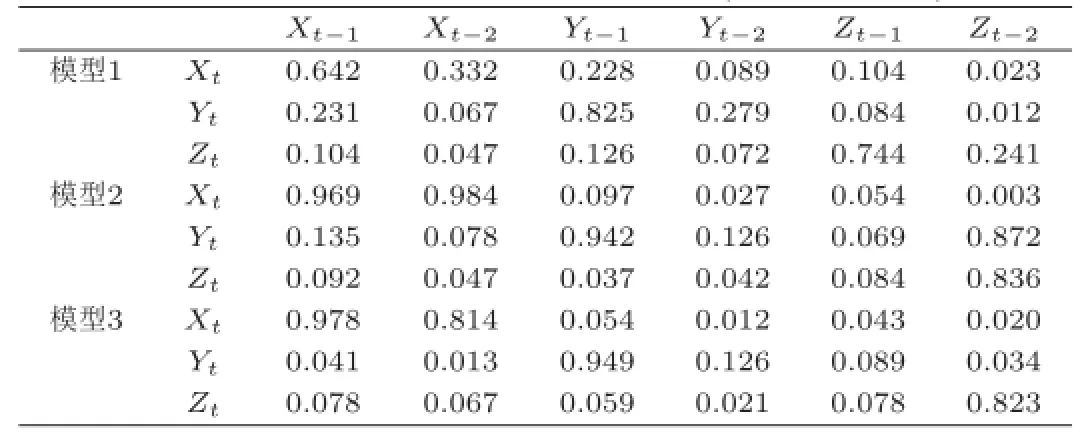
表6 GLR算法所得模型滞后因果关系比率(局部多项式估计)

表7 GLR算法所得模型滞后因果关系比率(局部线性估计)

表8 PC算法所得模型滞后因果关系比率

表9 ARM算法所得模型滞后因果关系比率
表1-表4给出了不同算法所得到的三个因果模型的同期因果关系.模拟结果显示,除了模型1之外,ITM算法对于模型2和模型3都能得到理想的结果.对于模型1,ITM算法虽然能正确的捕捉到所有同期变量之间的关系,但无法确定因果方向,造成这一结果的主要原因在于ITM算法主要利用条件互信息来给出变量间的因果关系,而仅仅由条件I(Xt,Zt|Yt)≤I(Xt,Zt)是无法区分结构Xt→Yt→Zt和Zt→Yt→Xt,事实上此时得到的是等价结构关系.表5则给出的是由ITM算法所得到的三个模型的滞后因果关系.ITM算法能正确的辨识原模型中几乎所有的滞后因果关系,只是在模型1中,关于Xt-1→Yt和Yt-1→Zt的模拟结果稍显偏大.
表1,表6和表7的模拟结果显示,对于三个模型,GLR方法都能正确的确定同期变量之间的因果关系.对于三个模型中所蕴含的滞后因果关系,相比于ITM方法,GLR方法虽然能正确的确定原模型中几乎所有的滞后因果关系,但也产生过多的因果关系.如基于局部线性估计的GLR方法所得模型2的结果以及基于局部多项式估计的GLR方法所得模型1的结果.从所有的结果可以看出,当采用局部多项式估计时,对于非线性模型2和模型3,GLR方法能够得到更为满意的结果.然而对于线性模型1,GLR方法得到的结果较差,可能原因在于构造GLR统计量时,采用的是局部二次多项式拟合原模型,从而对于线性模型1可能会造成更大的偏差.采用局部线性估计法得到的GLR方法所得结果情况则恰恰相反.这说明在使用GLR方法辨识变量间的因果关系时,模拟的结果也依赖于构造的GLR统计量时所使用的估计法.因此,如果在试验前能够获取原模型一定的先验知识(如线性模型或是非线性模型),采用更为合理的估计方法,相应的会提高GLR方法所得结果的精确度.
表3和表8给出的是PC算法所得结果.模拟结果显示PC算法仅仅对于线性时间序列模型1所得到结果较好,而对于非线性可加模型2和非线性结构向量自回归模型3,PC算法得到的结果明显较差,由PC算法得到的模型2和3的因果结构明显缺失了较多的边,如模型2中的Xt-1→Xt和Yt-1→Yt,模型3中的Yt-1→Yt和Zt-1→Zt等.此结论也进一步证实了模型是线性模型与否对PC算法所得结果有着显著的影响.
表4和表9给出的是ARM方法所得结果.从模拟结果可以发现,由ARM算法得到的模型1和模型2的因果结构类似于ITM算法得到的结果.然而ARM算法得到模型3的结构和原模型由较大出入,它错误的去除了原模型中的许多因果关系,如Yt→Xt和Yt→Zt,造成这一现象的原因是因为模型3中同期变量间的因果关系是非线性的,违反了ARM算法使用的前提条件.
[1]Oxley L,Reale M,W ilson G.Constructing structural VAR models w ith conditional independence graphs[J].M athem atics and Com pu ters in Simu lation,2009,79:2910-2916.
[2]Eich lerM.Graphicalmodelling ofmu ltivariate time series[J].Probability Theory and Related Fields,2012,153:233-268.
[3]Gao Wei,Tian Zheng.Latent ancestral graph of structure vector autoregressivemodels[J]. Journal of System s Engineering and Electronics,2010,21:233-238.
[4]Hoover K.Automatic inference of the contem poraneous causal order of a system of equations[J].Econom etric Theory,2005,21:69-77.
[5]M oneta A.G raphical causalm odels and VARs:an em p irical assessm ent of the real business cycles hypothesis[J].Em pirical Econom ics,2008,35(2):275-300.
[6]Wei Yuesong,Tian Zheng,Xiao Yanting.Learning mu ltivariate time series causal graphs based on cond itionalmu tual in form ation[J].Jou rnal of System s Science and System s Engineering,2013,22:38-51.
[7]Chu Tian jiao,G lymour C.Search for additivenonlinear time series causalmodels[J].Journal of M achine Learning Research,2008,9:67-91.
[8]Wei Yuesong,Tian Zheng,Xiao Yanting.Learning causal graphs of non linear structural vector autoregressivemodelsusing information theory criteria[J].Journal of System s Science &Com p lexity,2014,27(6):1213-1226.
[9]Fan Jianqin,Zhang Chunm ing,Zhang Jian.Generalized likelihood ratio statistics and W ilks phenomenon[J].The Annals of Statistics,2001,29(1):153-193.
M R Su b jec t C lassifica tion:62M 10
Generalized likelihood ratio app roach fo r iden tifying non linear structu ral vector au toregressive causal graphs
WEIYue-song
(School of M athem atical Science,Huaibei Norm al University,Huaibei 235000,China;Department of App lied M athematics,Northwest Polytechnical University,Xi’an 710129,China)
In this paper,the causal relationships among variables of nonlinear structure vector autoregressivemodel are studied using graphicalmodelmethod.The non linear structure vector autoregressive causal graph is p resented,and a generalized likelihood ratio app roach is developed to in fer the causal relationships.The generalized likelihood ratio statistics of contem poraneous and lagged are presen ted respectively,and a bootstrap m ethod is considered for determ ining the nu ll distribu tion of the test statistic.The validity of the p roposed method is con firmed by simu lations analysis.
nonlinear structu ral vector autoregressivem odels;graphicalm odels;conditional independence;generalized likelihood ratio;bootstrap method
A
1000-4424(2016)02-0143-10
2015-01-28
2016-03-13
国家自然科学基金(60375003;61201323);安徽省高校自然科学研究项目(K J2015A 035)

