一类广义非线性Schr¨odinger扰动方程的泛函渐近解法

欧阳成，汪维刚，石兰芳，莫嘉琪（.湖州师范学院理学院，浙江湖州000；.桐城师范高等专科学校理工系，安徽桐城0；.南京信息工程大学数学与统计学院，江苏南京00；.安徽师范大学数学系，安徽芜湖00）

一类广义非线性Schr¨odinger扰动方程的泛函渐近解法

欧阳成1，汪维刚2，石兰芳3，莫嘉琪4
（1.湖州师范学院理学院，浙江湖州313000；2.桐城师范高等专科学校理工系，安徽桐城231402；3.南京信息工程大学数学与统计学院，江苏南京210044；4.安徽师范大学数学系，安徽芜湖241003）

研究了一类非线性Schr¨odinger扰动耦合系统.利用近似解相关联的特殊方法，首先讨论了对应的线性系统，并得到了其精确解.再利用泛函迭代的方法得到了非线性Schr¨odinger扰动耦合系统的泛函渐近解析解.这个渐近解是一个解析式，还可对它进行解析运算.这对使用简单的模拟方法得到的近似解是达不到的.

非线性方程；耦合系统；近似解

1　引言

众所周知，非线性Schr¨odinger方程在凝聚态物理，量子物理，流体力学，光学等领域中有很广泛的研究.其求解的方法不断地在改进和创新.很多学者做了许多工作［1-5］.目前，用近似解析方法就是一个新的求解的方法.它改变了单纯用数值模拟来求解的性态，而是由解析理论方法得到解的近似表达式.它的好处是可以由近似表达的解析式进一步通过解析运算来对解的性态作更深入的研讨［6-7］.目前许多近似解析方法在发展，包括平均法，合成展开发，边界层法，匹配法，同伦映射法和多重尺度法等等［8-11］.作者等也用近似解析方法讨论了一些非线性方程的问题［12-23］.因为光传播时具有波，粒二重性，Schr¨odinger方程就是这类光学模型之一.非线性Schr¨odinger方程已经被广泛应用在现代光通信技术中.而光通信的理论就是涉及光的传播.它具有广泛的研究背景和前景.本文是利用一种改进的泛函迭代近似解析方法研究了一类广义Schr¨odinger扰动耦合模型.

考虑如下一类广义非线性Schr¨odinger扰动耦合模型：

其中u（x，t），v（x，t）为对应系统的物理场函数；ai，bj（i=1，2，3，j=1，2）为对应物理量的加权参数；f.g为物理场函数的扰动项，hi（i=1，2，3）为场函数的初始函数，它们是在相应的变化范围内的充分光滑的函数.本系统代表了一类光导纤维中光传播并具有受到场函数的速率非线性扰动广义传播系统的模型.马松华等［24］研究了该系统脉冲解，飞秒孤波的激励，以及讨论了传播解间的弹性相互作用.其详细物理背景参见文献［24-25］.现用一个简单而有效的解析方法来求得广义Schr¨odinger扰动耦合模型（1）-（3）的近似解析解.

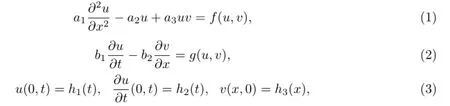
2　无扰动耦合系统

先考虑如下对应的无扰动情形简单的耦合系统

并满足初始条件（3）的解.显然，（4），（5）的解为

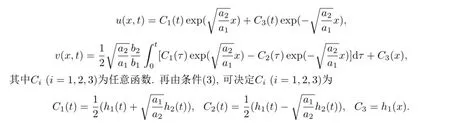
于是问题（3）-（5）的解为

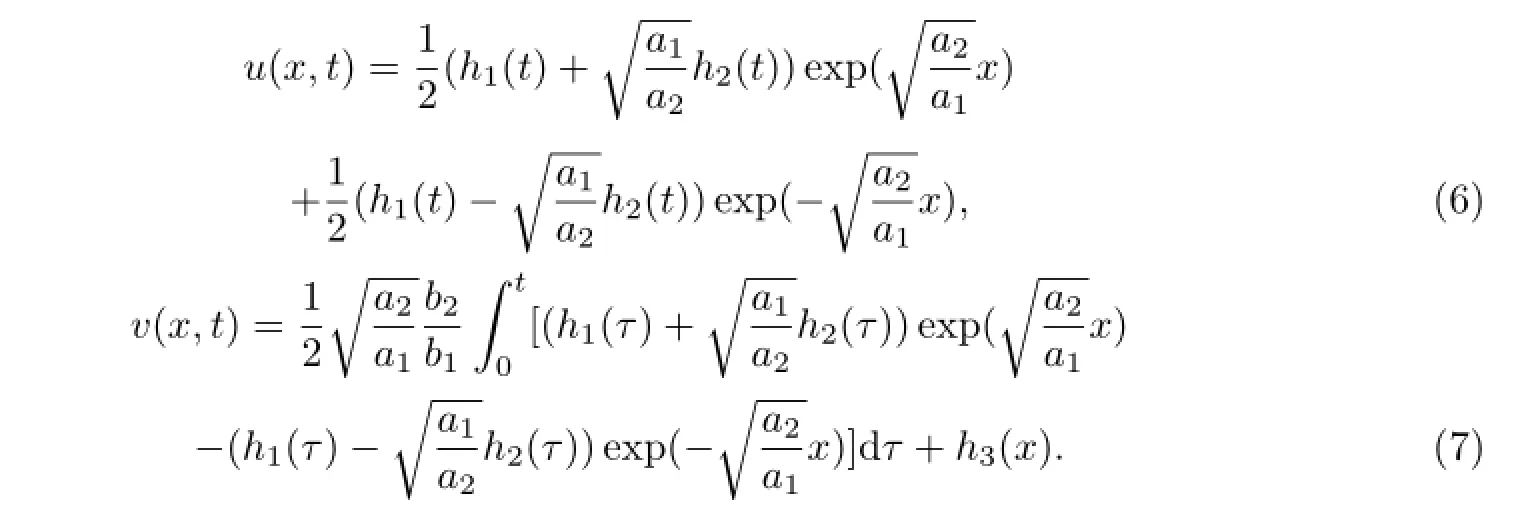
作为一个特殊情形，由（1）-（3）式，当ai=bj=1（i=1，2，3，j=1，2），h1=sin t，h2=h3= 0时，由（6），（7）式得到的问题（3）-（5）的场函数u（x，t），v（x，t）的曲面图形分别由图1和图2所示.

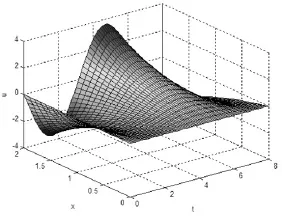
图1　问题（3）-（5）的场函数的曲面图

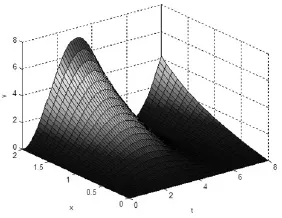
图2　问题（3）-（5）的函数的曲面图

3　构造非线性扰动模型渐近解的迭代式

由于非线性耦合模型（1）-（3）一般不能得到有限项初等函数形式的精确解.因此需要求出非线性扰动Schr¨odinger耦合模型（1）-（3）解的近似表示式.

为了求得广义非线性Schr¨odinger扰动耦合模型（1）-（3）的近似解.现构造如下泛函F［u］∈C1（R）：

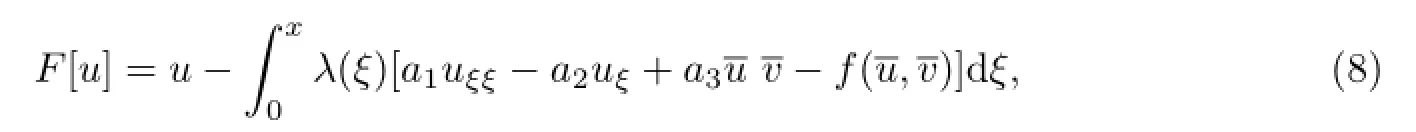
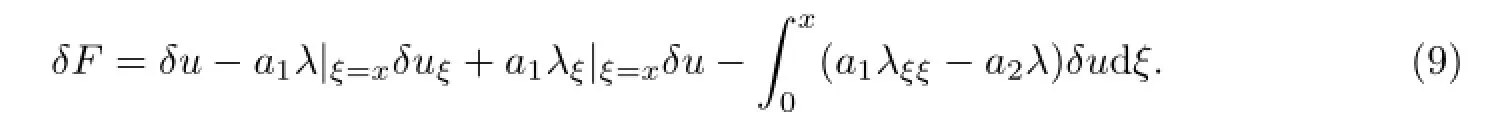
在（9）式中，令δF=0.可得到Lagrange乘子应满足的关系式：

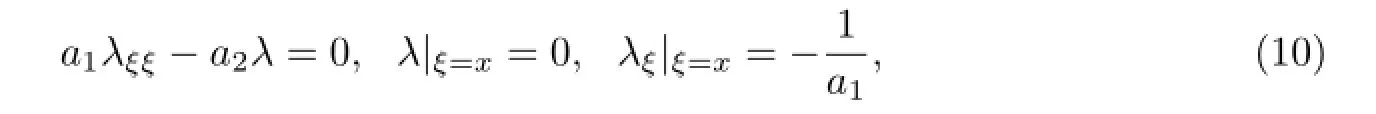
由（10）式，不难得到：

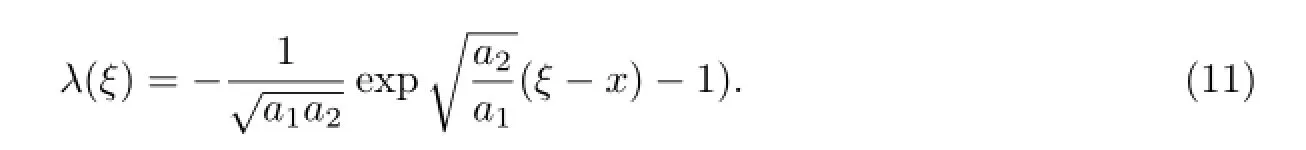
由（8），（11）式，现构造如下的渐近解的广义迭代式：

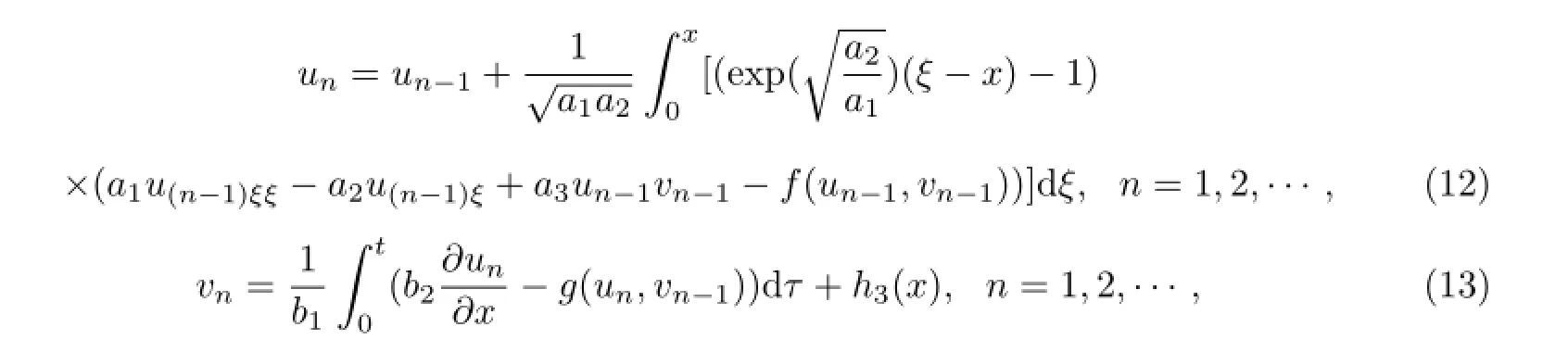
其中（13）式的un由（12）式表示.由渐近解的广义泛函迭代式（12）和（13）式，并适当选取初始迭代u0，v0，便可依次地得到广义非线性耦合模型（1）-（3）的任意次近似解.

4　扰动耦合模型的泛函渐近解

首先选取（1）-（3）相关的线性齐次问题（3）-（5）的解（6），（7）为渐近解的泛函迭代式（12），（13）的初始迭代u0，v0.即

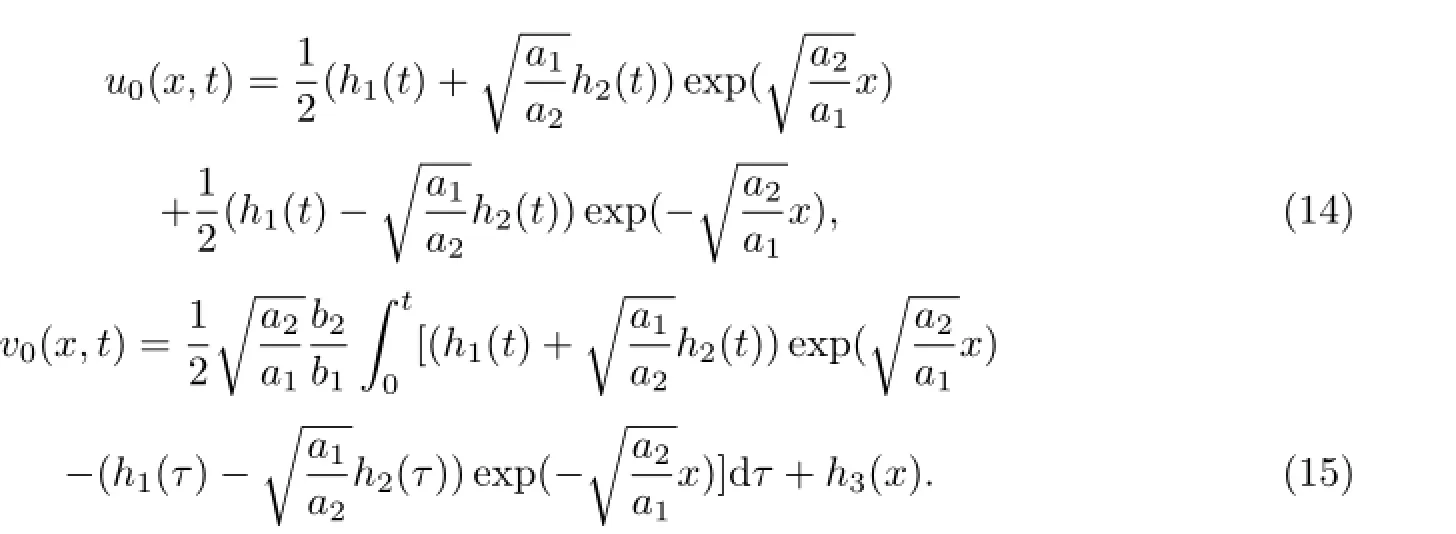
由渐近解的泛函迭代（12）和（13）式，可以得到广义非线性Schr¨odinger扰动耦合模型（1）-（3）的一次泛函迭代解u1app，v1app：

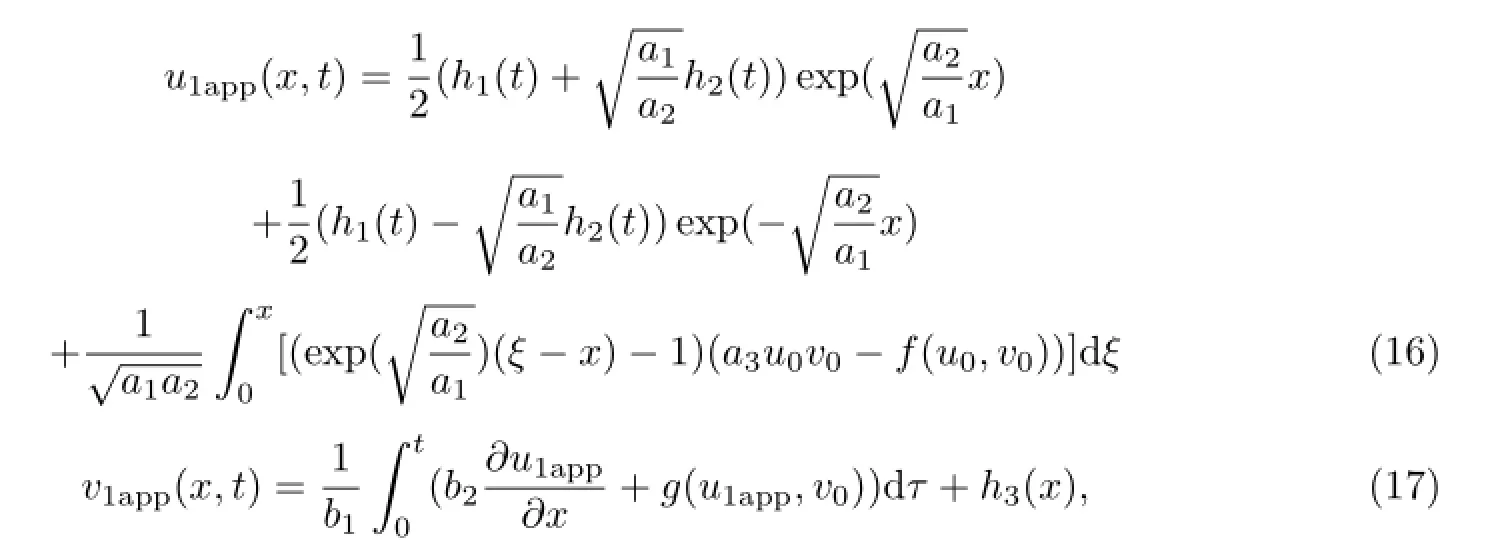
其中u0，v0由（14），（15）式表示，（17）式中的u1app由（16）式表示.

继续由渐近解的泛函迭代（12）和（13）式，可以得到广义非线性Schr¨odinger扰动耦合模型（1）-（3）的二次泛函迭代解u2app，v2app：

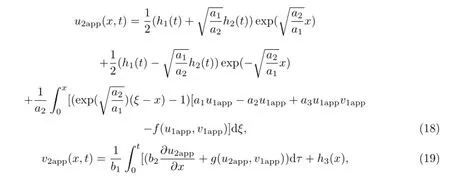
其中u1app，v1app由（14）-（17）式表示，（19）式中的u2app由（18）式表示.

同样，由（12）和（13）式，可以依次得到广义非线性Sch r¨od inger扰动耦合模型（1）-（3）的各次泛函迭代解unapp，vnapp.

可以用泛函分析和不动点理论证明［26-27］，由上述得到的近似解析函数序列｛unapp，vnapp｝在自变量的有限区域范围内是一致收敛的.

设

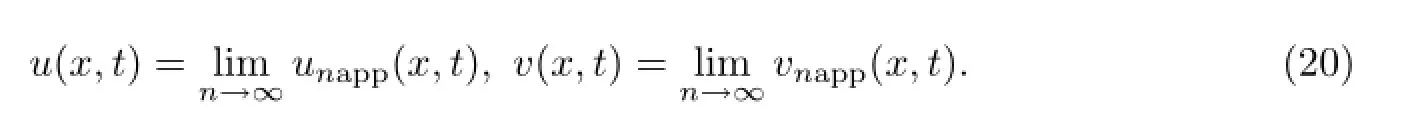
将（12）和（13）式两边取极限n→∞，显然，由（20）式确定的极限函数（u（x，t），v（x，t））就是广义非线性Schr¨odinger扰动耦合模型（1）-（3）的一组精确解（uexa（x，t），vexa（x，t））.因而，

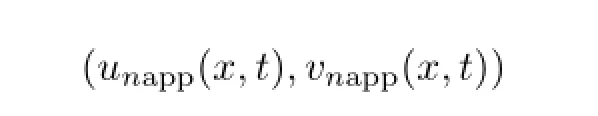
就是扰动方程模型（1）-（3）对应精确解（uexa（x，t），vexa（x，t））的n次泛函近似解析解.

5　举例

为简单起见，考虑一个特殊的非线性Sch r¨od inger扰动耦合模型，其系数为ai=bi=1（i= 1，2），a3=ε，h1=sin t，h2=h3=0，f=εu2，g=0，其中ε为正的小参数.这时由模型（1）-（3）得到的广义非线性Schr¨odinger扰动耦合模型为

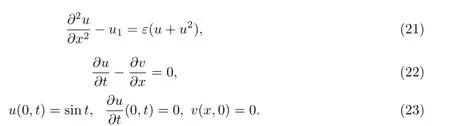
采用渐近解的广义迭代方法来求广义非线性Schr¨odinger扰动耦合模型（21）-（23）的近似解析解.由（14），（15）式得到初始迭代：

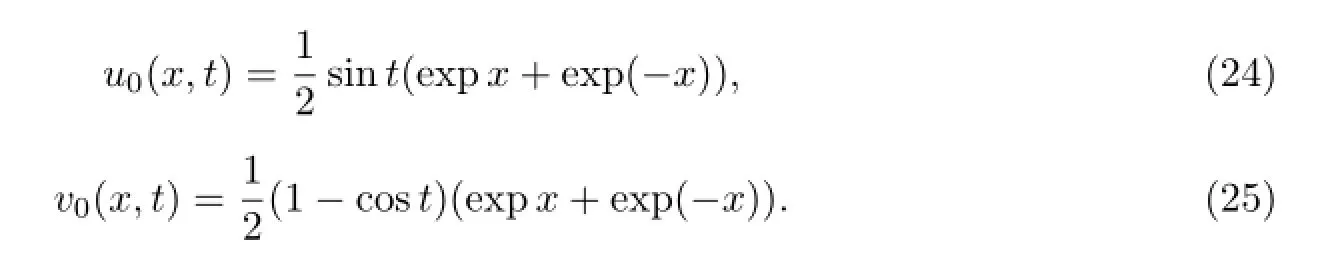
再由（16），（17）式可得广义非线性Schr¨odinger扰动耦合模型（21）-（23）的一次近似解u1app，v1app：

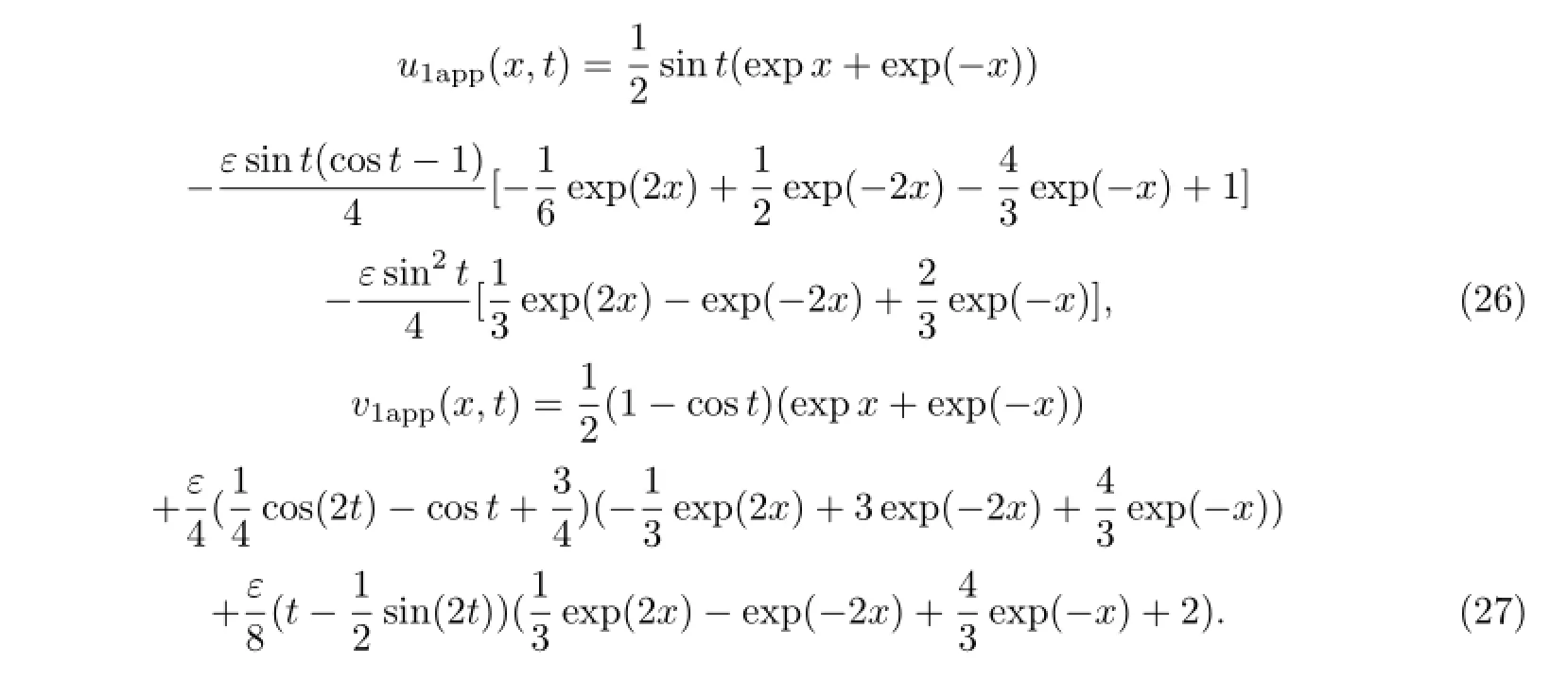
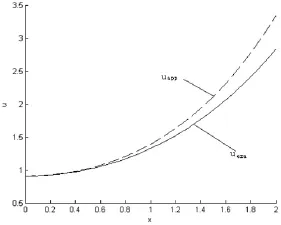
图3　问题（21）-（23）的场函数u（x，t）

图4　问题（21）-（23）的场函数v（x，t）

由（26）式，并取t=2以及ε=0.5和ε=0.05，可以用模拟的方法画出场函数的近似解析式u1app和精确式uexa的曲线比较图形（参见图3，图4）.又从图3-4看出，用广义泛函渐“接近”而且随参数ε越小，近似程度就越高.同样，场函数v也有相同的情形.

继续地，由（18）-（19）式可以得到广义非线性Schr¨odinger扰动耦合模型（21）-（23）的二次泛函近似解u2app，v ：

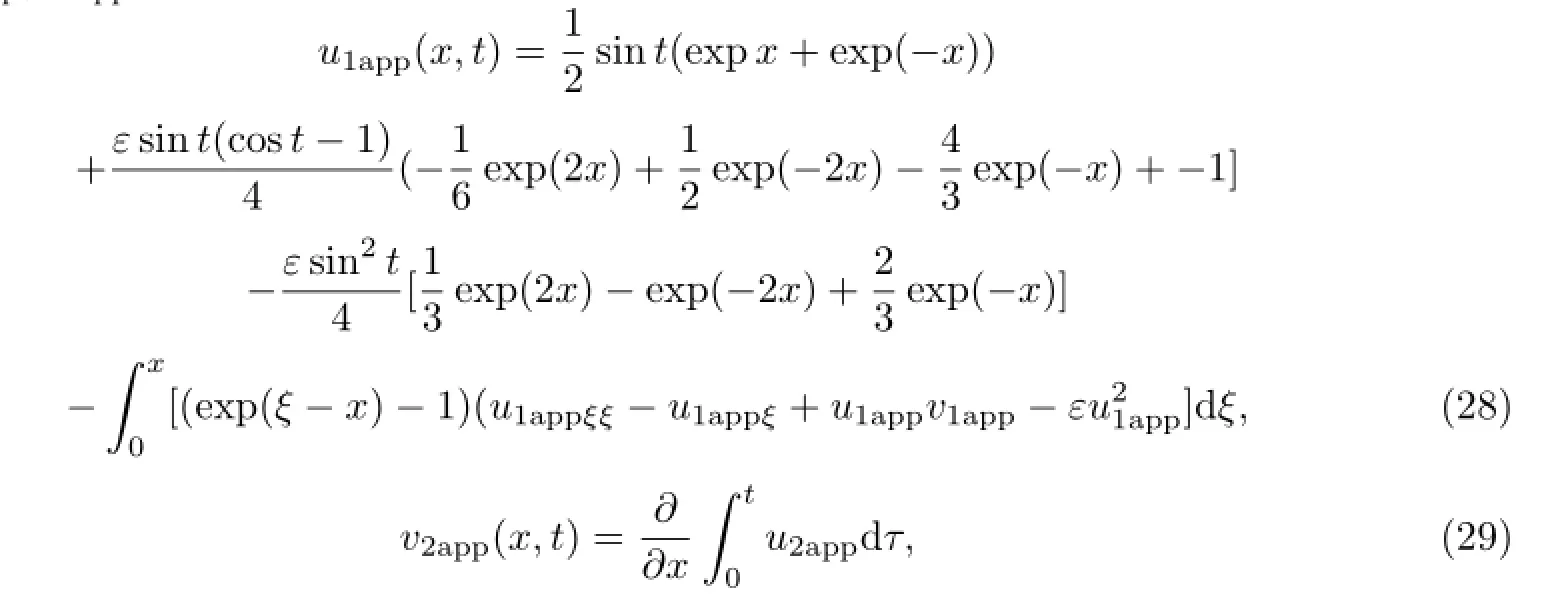
其中u1app，v1app由（26），（27）表示，（29）式中的u2app由（28）式表示.

同样，由渐近解的广义泛函迭代（12）和（13）式，可以依次得到广义非线性Schr¨odinger扰动耦合模型（21）-（23）的各次泛函近似解unapp，vnapp（n=3，4，···）.

又因为广义非线性Schr¨odinger扰动耦合模型（21）-（23）的ε为正的小参数，所以还能用摄动理论以及不动点定理证明，非线性Schr¨odinger扰动耦合模型（21）-（23）的第n次摄动渐近解有如下的估计式

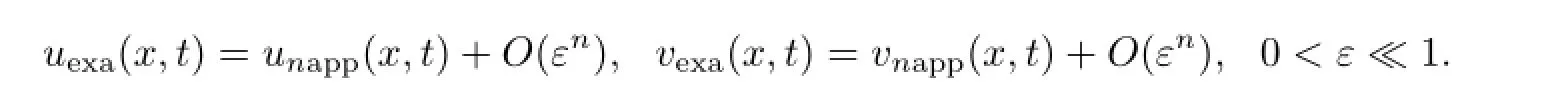
因此，利用本文提出的近似方法得到的近似解从上述侧面来看，也具有较好的精确度.

6　广义泛函迭代方法讨论

用广义泛函迭代方法来求非线性方程的物理问题的近似解析解是当前发展起来的一种方法，其方法和理论还在不断的创新中.本文就是在经过改进的方法上来讨论广义非线性Schrodinger模型，并取得了良好的结果.

本方法得到的是用数学解析式来表述对应模型的近似解，因而对所得的各次近似式还可以进行微分，积分等解析运算.所以它能得到与原未知函数有关物理量的近似表达式.然而，使用常规的龙格库塔法，差分法，有限元法，模拟法等数值方法一般是不能的.特别，本广义泛函迭代方法对于解具有突变型的特异性态的近似表达式能较简便地得到.但使用传统的数值解法，其运算过程就比较烦杂，而且一些较古典的方法往往会对具有突变等性态的区域内，诸如孤波，冲击层，转向点等的邻域内，其物理特性也往往会被忽略，因此在这些区域内会有与真实解有较大地偏离.

对非线性物理问题，利用解析式来表达问题的解，近来已经有一些研究，例如Jacobi椭圆函数法，双曲函数展开法，修正的CK方法，非经典李群方法，齐次平衡法等.这些方法在一定的场合下，能得到很好的结果.但是这些方法的求解，往往只使用于具体的特殊非线性方程.可求解的面受到一定的限制.然而，本文所涉及的广义泛函迭代方法求近似解的面比较广，它对方程的非线性项的表示式不必很具体.甚至是一般表示式也能通过本广义泛函迭代的通式，得到相应问题的各次泛函近似解析解.

此外，广义泛函迭代方法还有一个与其它求近似解析解的方法不同的特点，就是广义泛函迭代方法是建立在泛函分析的函数空间下进行的，因此讨论的对象无论是物理模型的结构，还是近似解都是可在泛函分析的广义函数空间意义下进行的.在量子力学，弹性力学，热力学，激波理论等等的物理学科中许多问题都涉及到广义函数的概念，譬如”点源函数”就是在许多现代物理学科中出现的一个广义函数.

在本文中得到了广义非线性Schr¨odinger扰动耦合模型的近似解析解，是采用广义泛函迭代方法与其它方法相结合的情况下得出的近似解.先用其它相应的方法求出Schr¨odinger非线性方程的退化问题解，然后以此解析解为广义泛函迭代关系式的初始近似，然后利用广义泛函迭代式依次地得到各次泛函近似解析式.

同时，用广义泛函迭代方法求解广义Sch r¨od inger非线性扰动耦合模型的近似解析解，在一定的意义下，还可以较快地得到近似解析解所要求的精度.例如，在本文的举例中就说明了用广义泛函迭代方法求解非线性扰动耦合模型的泛函近似解析解具有良好的精度.

7　近似解析解的物理意义

用广义泛函迭代方法求解广义Schr¨odinger非线性扰动耦合模型的泛函近似解析解及其得到的模拟图，可以看出对应系统的物理场函数的通量，峰值和其它有关的物理量的趋势等性态，并且可以看出其结果符合实际情况的规律的程度.而且还可看出对应系统的物理场函数其强度和其它有关参数，使得模型的物理场函数达到最佳状态.根据所述的分析和计算，以及用广义解析的方法来获得解的解析表达式.并通过数学解析表示式对模型的各物理量性态可作更深入的解析分析，使得对问题的发展趋势有一个更好的结果.

由上述提供的方法还可继续得到更高次的泛函近似解析解.以便得到更精确的结果，使得与模型的实际情况更接近.

8　结论

非线性Schr¨odinger扰动方程出自于一类复杂的自然现象.因此需要简化它为基本模型.利用近似方法求解这类模型是非线性理论的重要方面.本文就是利用广义泛函迭代原理构造了一个简单而有效地非线性Sch r¨od inger耦合系统模型的近似解析解.

由广义泛函迭代方法求出对应广义非线性Schr¨odinger扰动耦合模型（21）-（23）的泛函近似解析解，不同于一般单纯的由模拟得到的数值近似解，因为由广义泛函方法得到的广义泛函近似解是具有解析形式的结构，因此它还可以进行微分，积分等解析运算，从而能进一步地对相应解的其它物理量得到更深入的性态研究.

［1］Parkes E J.Some periodic and solitary travelling-wave solutions of the short-pu lse equation［J］.Chaos Solitons Fractals，2008，38（1）:154-159.

［2］Sirendaoreji，Sun Jiong.Auxiliary equation method for solving nonlinear partial differential equations［J］.Phys Lett A，2003，309（5-6）:387-396.

［3］M cPhaden M J，Zhang Dongxiao.Slow dow n of them erid ionaloverturning circu lation in the upper Pacific ocean［J］.Nature，2002，415（3）:603-608.

［4］潘留仙，左伟明，颜家壬.Landau-G inzbu rg-Higgs方程的微扰理论［J］.物理学报，2005，54（1）: 1-5.

［5］封国林，戴兴刚，王爱慧，等.混沌系统中可预报性的研究［J］.物理学报，2011，50（4）:606-611.

［6］何吉欢.工程和科学计算中的近似非线性分析方法［M］.郑州:河南科学技术出版社，2002.

［7］He Jihuan，W u Xuhong.Construction of solitary solution and com pacton-like solution by variational iteration m ethod［J］.Chaos Solitions&Fractals，2006，29（1）:108-113.

［8］Ni W eim ing，W ei Juncheng.On positive solution concentrating on spheres for the G ierer-Meinhardt system［J］.JDiffer Equations，2006，221（1）:158-189.

［9］Bartier Jean-Philippe，G lobal behavior of solutions of a reaction-diffusion equation w ith grad ient absorp tion in unbounded dom ains［J］.A sym p Anal，2006，46（3-4）:325-347.

［10］Libre J，da Silva P R，Teixeira M A.Regu larization of discontinuous vector fields on R3 via singu lar perturbation［J］.JDyn Differ Equations，2007，19（2）:309-331.

［11］Guarguaglini F R，Natalini R.Fast reaction lim it and large time behavior of solutions to a non linearmodel of sulphation phenomena［J］.Commun Partial Differ Equations，2007，32（2）: 163-189.

［12］Mo Jiaqi.Homotopiv mapping solvingmethod for gain fluency of a laser pu lse am p lifier［J］. Science in China，Ser.G，2009，52（7）:1007-1010.

［13］M o Jiaqi，Lin Shirong.The hom otop ic m app ing solu tion for the solitary wave for a generalized non linear evolution equation［J］.Chin Phys B，2009，20（9）:3628-3631.

［14］Mo Jiaqi.Solution of travelling wave for non linear disturbed long-wave system［J］.Commun Theor Phys，2011，55（3）:387-390.

［15］M o Jiaqi，Chen X ian feng.Hom otop ic m app ing m ethod of solitary wave solu tions for generalized com p lex Burgers equation［J］.Chin Phys B，2010，21（10）:100203.

［16］Mo Jiaqi，Wang Weigang，Chen Xian feng，et al.The shock wave solutions for singularly perturbed time delay non linear boundary value p rob lems w ith two papameters［J］.M ath Appl，2014，27（3）:470-475.

［17］石兰芳，莫嘉琪.用广义变分迭代理论求一类相对转动动力学方程的解［J］.物理学报，2013，52（4）:040203.

［18］石兰芳，林万涛，林一骅，等.一类非线性方程类孤波的近似解法［J］.物理学报，2013，62（1）: 010201］.

［19］石兰芳，朱敏，周先春，等.一类非线性发展方程孤立子行波解［J］.物理学报，2014，63（13）: 130201.

［20］石兰芳，汪维刚，莫嘉琪.高维扰动破裂孤子方程行波解的渐近解法［J］.应用数学，2014，27（2）: 317-321.

［21］Wang Weigang，Shi Lanfang，Xu Yonghong，et al.Generalized solution of the singularly pertu rbed boundary value p roblem s for sem ilinear ellip tic equation of higher order w ith tw o parameters［J］.JNankaiUniv，2014，47（2）:47-81.

［22］汪维刚，林万涛，石兰芳，等.非线性扰动时滞长波系统孤波近似解［J］.物理学报，2014，63（11）: 110204.

［23］Wang Weigang，Shi Juanrong，Shi Lan fang，et al.The singu larly perturbed solution of non linear non local equation for higher order［J］.J Nankai Univ，2014，47（1）:13-18.

［24］马松华，方建平.联立Schr¨odinger系统新精确解及其所描述的孤子脉冲和时间孤子［J］.物理学报，2006，65（11），5611.

［25］李帮庆，马玉兰，徐美萍，等.耦合Schr¨od inger系统的周期振荡折叠孤子［J］.物理学报，2011，60（6）:060203.

［26］Barbu L，M orosanu G.Singu larly Perturbed Boundary-Value Problem s［M］.Basel: Birkhauserm Verlag，2007.

［27］de Jager E M，Jiang Fu ru.The Theory of Singu lar Perturbation［M］.Am sterdam:North-Holland Pub lishing，1996.

M R Sub ject C lassification:35B25

A class of functional asym p totic m ethod for the generalized non linear d istu rbed Sch r¨od inger equation

A class of the generalized disturbed non linear Schr¨odinger coup led system is studied. Using the specific technique relates to the approxim ate solu tions，the corresponding linear system is first considered and its exact solution is obtained.Then，the functional asym p totic analytic solution of the non linear Schr¨odinger d istu rbed coup led m odel is found by using a valid m ethod.The obtained asym p totic solution is an analytic expression，so it cou ld also carry on analytic operations.These cannot happen to the sim ple simu latemethod.

non linear equation；coup led system；app roximate solution

O 175.29

A

1000-4424（2016）02-0176-09

2015-02-12

2016-03-10

国家自然科学基金（11202106）；浙江省自然科学基金（LY 13A 010005）；江苏省自然科学基金（13KJB 170016）