一类具有扩散和Beddington-DeAngelis反应函数的病毒模型的全局稳定性
杨 瑜,周金玲(浙江外国语学院科学技术学院,浙江杭州310012)
一类具有扩散和Beddington-DeAngelis反应函数的病毒模型的全局稳定性
杨瑜,周金玲
(浙江外国语学院科学技术学院,浙江杭州310012)
研究了一类具有扩散和Beddington-DeAngelis反应函数的病毒模型.通过构造Lyapunov函数,证明了模型的感染平衡点是全局渐近稳定的.
病毒模型;扩散;Lyapunov函数;全局稳定性
1 引言
考虑到病毒的空间迁移效应对病毒感染过程的影响,文献[1]研究如下反应扩散模型

这里u(x,t),v(x,t)和w(x,t)分别表示未感染细胞,感染细胞和游离病毒在空间位置x处和时刻t的浓度.γ,α,β,p,k,s都是正常数.d>0是病毒的扩散系数.Δ是Lap lace算子.
在系统(1)的基础上,文献[2]利用比较原理研究一类具有时滞和Holling-II反应函数的反应扩散病毒感染模型的全局稳定性.而文献[3]通过构造Lyapunov泛函研究一类具有Beddington-DeAngelis反应函数的时滞反应扩散病毒模型的全局稳定性和行波解的存在性.利用Lyapunov函数(泛函)研究反应扩散模型(时滞反应扩散模型)的全局稳定性是一种比较有效的方法.在此基础上,文献[4]和[5]通过构造Lyapunov泛函分别研究具有更一般反应函数的时滞反应扩散病毒模型的全局稳定性.注意到上述文献中均假定病毒可以自由迁移,而未感染细胞和感染细胞不能迁移.而文献[6]和[7]考虑未感染细胞,感染细胞和病毒均可自由迁移.
最近,文献[8]讨论如下一类具有扩散和Beddington-DeAngelis反应函数的病毒模型

其中a和b是正常数.Ω∈Rn是有界光滑区域,且边界∂Ω充分光滑,ν是边界上的单位外法向量.结果表明:当基本再生数R0<1时,未感染平衡点是全局渐近稳定的;当基本再生数R0>1时,感染平衡点是局部渐近稳定的.但是,感染平衡点的全局渐近稳定性并未被讨论.
本文将通过构造Lyapunov函数研究系统(2)的感染平衡点的全局渐近稳定性.该方法已被一些学者用来研究不同反应扩散模型的全局稳定性(见文献[9-16]).
本文内容安排如下:§2给出一些基本结果.§3证明系统(2)的感染平衡点是全局渐近稳定的. §4通过数值模拟验证所得理论结果的正确性.
2 基本结果
本节给出系统(2)已有的一些结果,见文献[8].系统(2)的基本再生数

当R0≤1时,系统(2)只有一个未感染平衡点时,系统(2)还有一个感染平衡点E∗=(u∗,v∗,w∗),其中

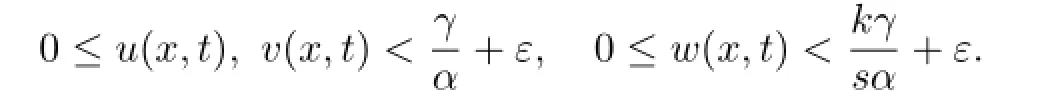
定理2.2当R0<1时,E0是局部渐近稳定的;当R0>1时,E∗是局部渐近稳定的,E0是不稳定的.
定理2.3当R0<1时,E0是全局渐近稳定的.
3 感染平衡点的全局稳定性
本节,通过构造Lyapunov函数讨论感染平衡点的全局渐近稳定性.为计算方便,记

定理3.1当R0>1时,E∗是全局渐近稳定的.
证定义Lyapunov函数

其中
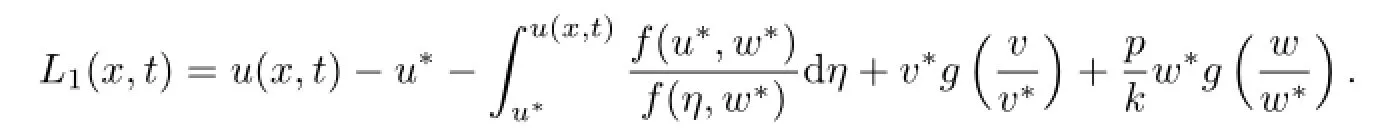
这里函数g(y)=y-1-ln y.易证g(y)在区间(0,+∞)的最小值为g(1)=0.
注意到

从而有
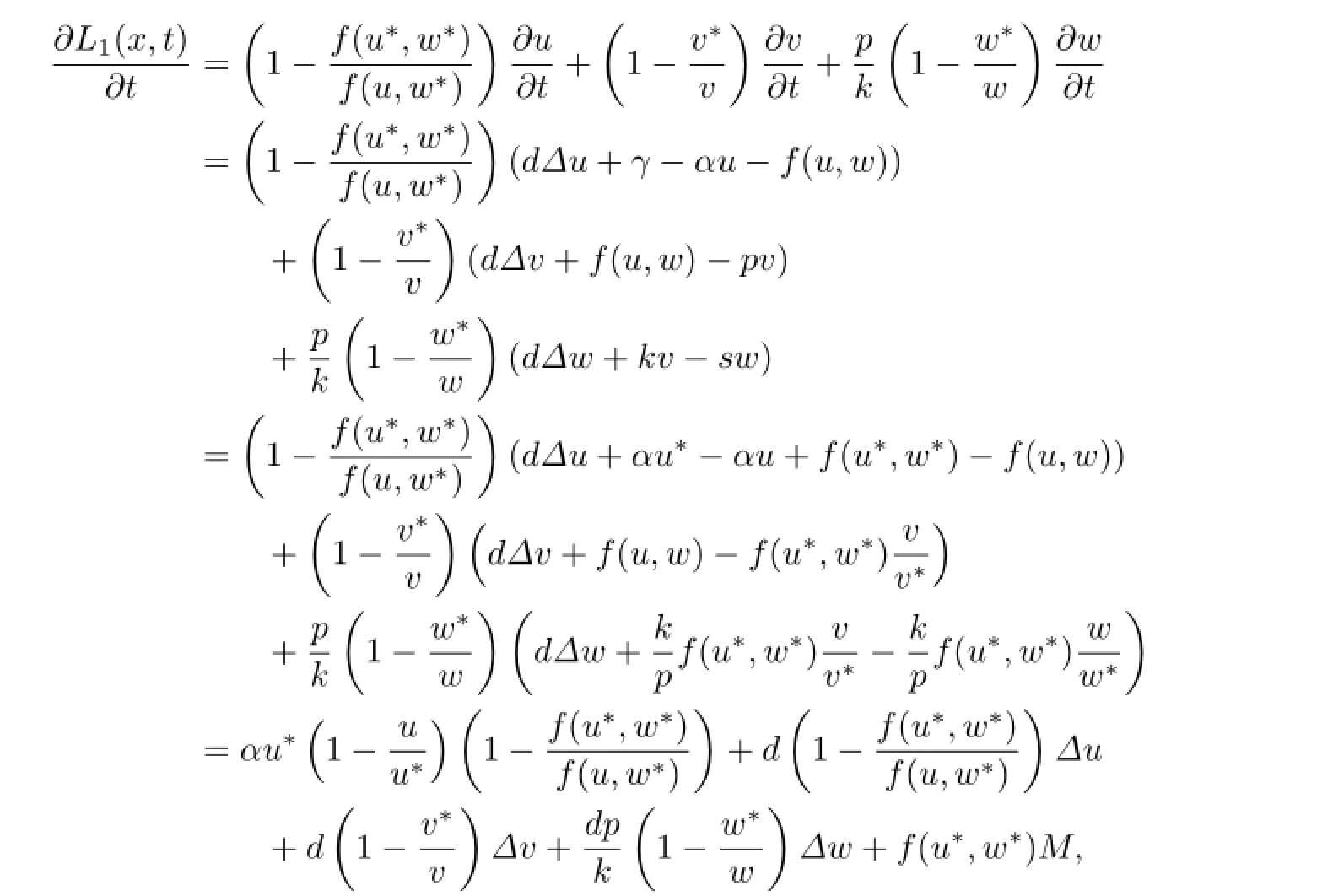
其中
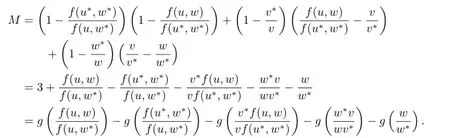
通过简单计算,得

和


利用

以及

可得

4 讨论与数值模拟
在文献[8]的基础上,本文进一步研究一类具有扩散和Beddington-DeAngelis反应函数的病毒模型.通过构造Lyapunov函数,证明了系统(2)的感染平衡点是全局渐近稳定的.
下面通过数值模拟来说明本文所得理论结果的正确性.

图1 当R 0=0.7212<1时,未感染平衡点E0=(125,0,0)是全局渐近稳定的
首先,取γ=15,α=0.12,β=0.00002,a=0.2,b=0.02,p=0.01,k=30,s=0.4和d=0.2.容易计算R0=0.7212<1.由定理2.3知,系统(2)的未感染平衡点E0=(125,0,0)是全局渐近稳定的,见图1.
其次,取β=0.00006,而其它参数的取值不变.此时,R0=2.1635>1.定理3.1意味着系统(2)的感染平衡点E∗=(123.3425,19.8904,1491.8)是全局渐近稳定的,见图2.

图2 当R0=2.1635>1时,感染平衡点E∗=(123.3425,19.8904,1491.8)是全局渐近稳定的
[1]Wang Kaifa,Wang Wendi.Propagation of HBV w ith spatial dependence[J].Mathematical biosciences,2007,210(1):78-95.
[2]Xu Rui,M a Zhien.An HBV m odel w ith d iffusion and tim e delay[J].Journal of Theoretical Biology,2009,257(3):499-509.
[3]Zhang Yiyi,Xu Zhiting.Dynam ics of a diffusive HBV model w ith delayed Beddington-DeAngelis response[J].Non linear Analysis:RealW orld A pp lications,2014,15:118-139.
[4]Hattaf K,Yousfi N.A generalized HBV m odel w ith diffusion and two delays[J].Com puters &M athematicsw ith Applications,2015,69(1):31-40.
[5]M cCluskey C C,Yang Yu.G lobal stability of a diffusive virus dynam icsmodelw ith general incidence function and tim e delay[J].Non linear Analysis:Real W orld App lications,2015,25:64-78.
[6]Stancevic O,Angstmann C N,M urray JM,et al.Turing patterns from dynam ics of early HIV in fection[J].Bulletin of M athematical Biology,2013,75(5):774-795.
[7]Lai X iu lan,Zou Xingfu.Repu lsion effect on superin fecting virions by infected cells[J].Bulletin of M athematical Biology,2014,76(11):2806-2833.
[8]杨文彬,李艳玲,王珊珊.一类带有扩散和B-D反应项的病毒模型的稳定性分析[J].工程数学学报,2014,31(1):57-66.
[9]Fan Yonghong,LiWantong.G lobal asym p totic stability of a ratio-dependent predator-prey system w ith d iffusion[J].Jou rnal of Com pu tational and App lied M athem atics,2006,188(2): 205-227.
[10]Hattaf K,YousfiN.G lobal stability for reaction-diffusion equations in biology[J].Com puters &M athematicsw ith Applications,2013,66(8):1488-1497.
[11]KoW,Ryu K.Qualitative analysis of a p redator-p reymodelw ith Holling type II functional response incorporating a p rey refuge[J].Journal of Differential Equations,2006,231(2):534-550.
[12]彭锐,王明新.一个具有扩散和比例依赖响应函数捕食模型的定性分析[J].中国科学,2008,38(2):135-148.
[13]Peng Rui.Qualitative analysis on a d iffusive and ratio-dependent predator-prey m odel[J]. IMA Journal of Applied Mathematics,2013,78(3):566-586.
[14]Shi Hongbo,LiW antong,Lin Guo.Positive steady states of a diffusive predator-prey system w ith m odified Holling-Tanner functional response[J].Non linear Analysis:Real W orld Applications,2010,11(5):3711-3721.
[15]Tian Yan ling,Weng Peixuan.Stability analysis of diffusive p redator-p rey modelw ith modified Leslie-Gower and Holling-type III schem es[J].App lied M athem atics and Com pu tation,2011,218(7):3733-3745.
[16]Yang Wensheng,Li Yongqing.Dynam ics of a diffusive p redator-p rey model w ith modified Leslie-Gower and Holling-type III schem es[J].Com pu ters&M athem aticsw ith App lications,2013,65(11):1727-1737.
M R Su b jec t C lassifica tion:37B 25;92D 25
G lobal stability of a d iffusive v irus dynam ics m odel w ith Bedd ington-D eA ngelis incidence function
YANG Yu,ZHOU Jin-ling
(School of Science and Technology,Zhejiang International Stud ies University,Hangzhou,310012,China)
A diffusive virus dynam ics model w ith Beddington-DeAngelis incidence function is investigated.By constructing Lyapunov function,it is shown that the infection equilibrium is globally asym p totically stab le.
virusmodel;diffusion;Lyapunov function;global stability
O175
A
1000-4424(2016)02-0161-06
2015-08-10
2016-02-03
国家自然科学基金(11501519);浙江省自然科学基金(LQ14A 010004)

