例谈数学解题中“退”的艺术
雷亚庆
(江苏省南京市大厂高级中学,210044)
○解题思路与方法○
例谈数学解题中“退”的艺术
雷亚庆
(江苏省南京市大厂高级中学,210044)
华罗庚先生曾经说过:“复杂的问题要善于退, 退到最原始而不失去重要性的地方,是学好数学的一个诀窍”.我们在解数学题遇到困难时不妨借鉴华罗庚教授“退”的思想,及时调整解题方向.那么,如何退、退到哪里去呢?下面举例说明.
一、退到定义
例1定义在(-1,1)内的函数 f(x)=-5x+sin x,如果f(1-a)+f(1-a2)>0,则实数a的取值范围为______.
解原式可化为 f(1-a)>-f(1-a2)
因为f(x)为奇函数,所以
f(1-a)>f(a2-1).
又f ′(x)=-5+cos x<0在(-1,1)上恒成立,故f(x)为减函数.


反思定义、定理是对数学对象的本质属性的概括和内在规律揭示,只有深刻地理解概念的本质和定理所揭示的内在规律,才能灵活运用它来简化解题过程.本题若将f(x)解析式代入不等式,正面求解则较困难,而退到函数最原始的地方,利用函数奇偶性、单调性定义就方便了问题处理.
二、退到上位概念
例2已知等差数列{an}中的前n项和为Sn,若Sm=Sn,求Sm+n.
分析本题如果用数列的基本公式处理,会面临多个参数的化简与变形,费时且易错,若利用数列是特殊的函数,则可以考虑利用函数的性质求解.
解由于Sn是关于n的不含常数的二次函数,故不妨设相应的二次函数为f(x)=ax2+bx.
∵Sm=Sn即f(m)=f(n),
∴该二次函数f(x)的图象的对称轴为

∴由对称性可知f(m+n)=f(0)=0,
∴Sm+n=0.
三、退到基本图形
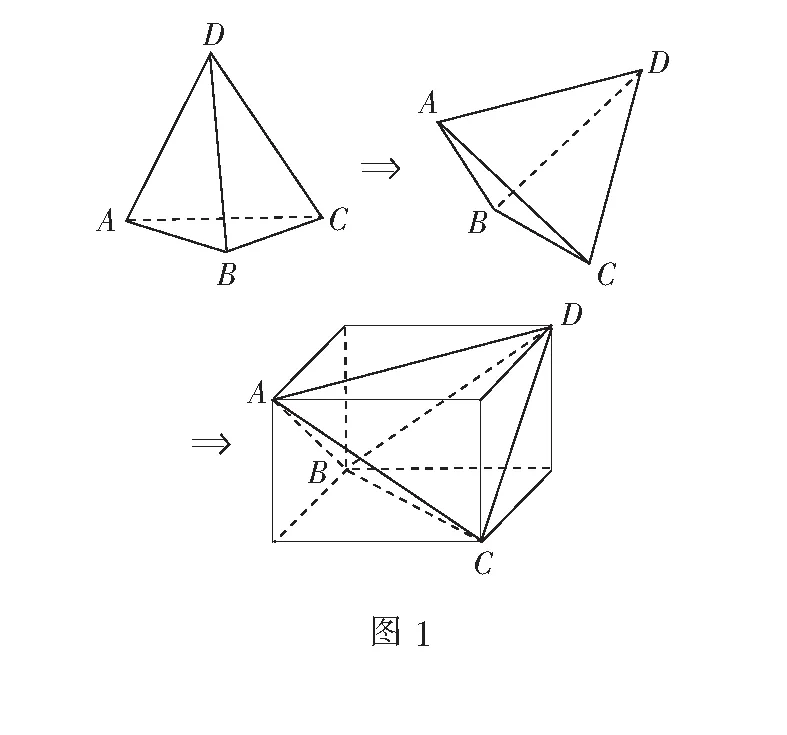
分析直接求解不易入手,因为从已知条件中很难确定球心的位置,进而半径也就无从算起了.这时我们不妨退一步想想,什么样的基本几何体的外接球球心和半径易确定呢?再仔细观察已知条件,我们就会发现是对棱两两相等,联想到长方体,于是问题迎刃而解.
解相对棱长相等的四面体,可考虑把它补成长方体(如图1),则四面体的三对对棱分别对应长方体的六个面的面对角线.设长方体的长宽高分别为x,y,z则有
解得x2+y2+z2=25,
即4R2=25,
所以S球=4πR2=25π.

分析这个问题如果从圆锥曲线的常规解法去处理将会十分繁琐,而从圆与椭圆的内在联系考虑,可把椭圆问题退回到圆的问题去解决.
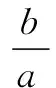
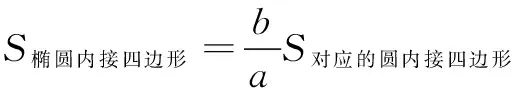
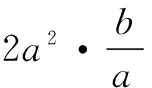
反思实际上很多棱具有特殊位置关系和长度关系的三棱锥的外接球问题都可以退回到长方体或正方体中得以顺利解决;同样,椭圆中很多重要性质都可以从圆的性质中拓展得到,有兴趣的同学们可以自行探究一下.
四、退到反面
分析A∩B≠∅的情况比较多,需要分类,所以不妨从反面出发考虑问题.先求A∩B=∅时a的取值集合,在取其补集即可得到本题的解.

若A∩B=∅,则a≤2,且a2+1≥4,
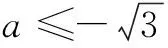
例6若下列方程:x2+4ax-4a+3=0, x2+(a-1)x+a2=0, x2+2ax-2a=0至少有一个方程有实根.试求实数a的取值范围.
分析三个方程至少有一个方程有实根的反面情况仅有一种:三个方程均没有实根,先求出反面情况时a的范围,再所得范围的补集就是正面情况的答案.
解设三个方程均无实根,则有
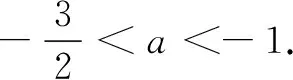
反思退到反面也就是我们常说的正难则反.一个问题如果从问题本身考虑情况较为复杂,需要过多的分类讨论,这时我们不妨退一退,退到它的反面也就是它的否定上去,就会化难为易,化繁为简!
五、由一般退到特殊
有一类填空题,条件任意但结论固定,这样的题目从常规做法入手往往比较繁琐,费时费力,我们可以采用特殊化的方法,退到特殊位置,特殊值或特殊图形去解决.

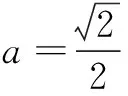
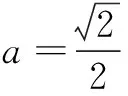
解不妨取∆ABC为以A为直角的直角三角形.则O为斜边BC的中点,所以

=6.
反思所谓“一般”是指人们追求普遍性认识的一种方式;而“特殊”是指人们深入个别认识的一种方式.当解决一般问题,直接找出结论规律或方法受阻时,往往考虑由某种特殊的或有限的情形,归纳推导到一般情形,即以一般向“特殊”后退的思想方法去探求规律和寻找解题方法.
六、动退到静

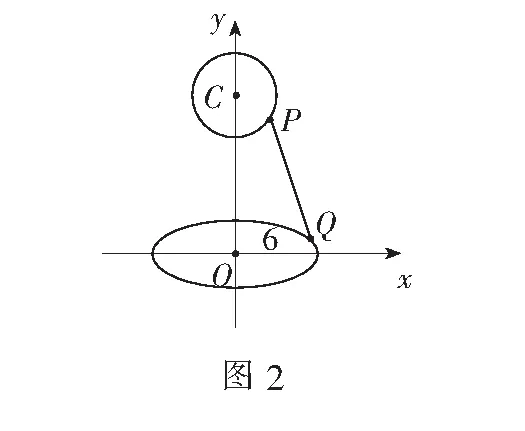
分析问题涉及到两个动点的最值问题,直接求解很困难.如何突破难点呢?这时我们不妨退一步,让Q先固定下来,问题就好解决了
解不妨先让点Q固定不动.
∵|PQ|≥|QC|-|PC|=|QC||-1,
当且仅当P,Q,C三点共线时取等号.
∴当|CQ|最小时,|PQ|也最小
这样问题就由求两个动点间的最短距离转化为求定点C(0,4)到椭圆上一点Q的最短距离.


(-1≤y0≤1),
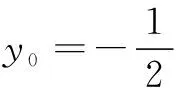



反思上述问题都涉及到多动点的最值问题,直接求解很困难,我们以退为进,以静制动,把多动点问题转化为单动点问题,而单动点问题的解决方法是我们很熟悉的,由此问题得以解决.
正所谓退一步海阔天空,这种以退为进的思想在解题中有时可发挥出突破性的作用.由复杂退到简单,由未知退到已知,由一般退到特殊,由正面退到反面,由高维退到低维,由动退到静,由不等退到等,由果退到因,退到我们最容易看清楚的地方,把问题简单化,让解题思路更加清晰,从而将复杂、难懂的数学问题顺利解决.

