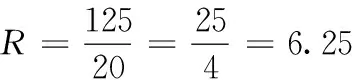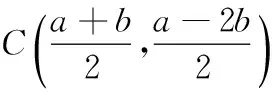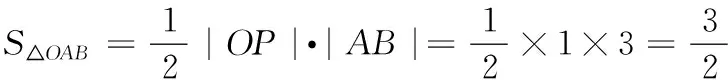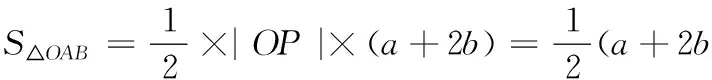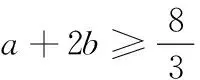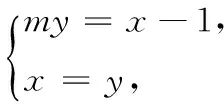高一数学测试



○课外测试○

高一数学测试

一、填空题(本大题共14小题，每小题5分，共70分)

1.若直线l过两点P(1,3)和Q(2,2),则l的斜率为______.

3.已知x+2y=6,则2x+4y的最小值为______.

4.若直线l上有两个点在平面α内,则下列说法正确的序号为______.

① 直线l上至少有一个点在平面α外;

② 直线l上有无穷多个点在平面α外;

③ 直线l上所有点都在平面α内;

④ 直线l上至多有两个点在平面α内.

5.直线x+a2y-a=0(a>0),当此直线在x,y轴上的截距和最小时,a的值为______.

6.在数列{an}中,a1=1,a11=3,且任意连续三项的和为9,则a2 016=______.

9.已知点P1(2,3)、P2(-4,5)和A(-1,2),则过点A且与点P1，P2距离相等的直线方程为______.

11.已知∆ABC的一条内角平分线CD的方程2x+y-1=0,两个顶点为A(1,2),B(-1,-1),则顶点C的坐标为______.

12.等比数列{an}中,an>0,a1=256,S3=448,Tn为数列{an}的前n项乘积,则当Tn取得最大值时,n=______.

13.已知正实数x,y满足x-y=xy,x-4y-a=0,则实数a的取值范围为______.

14.如图,一个箱子的每个面都是矩形且边长都是正整数,若它的对角线PQ=9,则这个箱子的体积最大可能值是______.

二、解答题(本大题共6小题,共90分.解答应写出必要的文字说明、证明过程或演算步骤)

15.(本小题满分14分)已知直线l1:(m-2)x+3y+2m=0,l2:x+my+6=0.

(1)若直线l1与l2垂直,求实数m的值;

(2)若直线l1与l2平行,求实数m的值.

16.(本小题满分14分)如图,在四棱锥P-ABCD中,ABCD是菱形,PA⊥平面ABCD.

(1)求证:BD⊥PC;

(2)若平面PBC与平面PAD的交线为l,求证:BC∥l.

17.(本小题满分15分)已知等比数列[an}满足2a1+a3=3a2,且a3+2是a2,a4的等差中项.

(1)求数列{an}的通项公式;

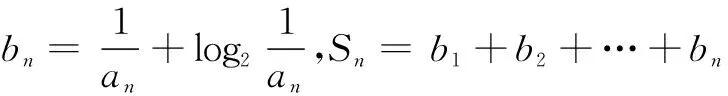
18.(本小题满分15分)为了做好促销活动,某电商打算将进行促销活动的礼品重新包装.设计方案如下:将一块边长为20 cm的正方形纸片ABCD剪去四个全等的等腰三角形∆SEE′,∆SFF′,∆SGG′,∆SHH′,再将剩下的阴影部分折成一个四棱锥形状的礼品袋S-EFGH,其中A,B,C,D重合于点O,E与E′重合,F与F′重合,G与G′重合,H与H′重合(如图所示),设AE=BE′=x(cm).

(1)求证:平面SEG⊥平面SFH;

(2)若电商要求礼品袋的侧面积不少于128 cm2,试求x的取值范围;

(3)当x=5时,该电商打算将礼品袋S-EFGH全部放入一个球形状的包装盒内密封,求包装盒的内径R的最小值.

19.(本小题满分16分)在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:2x+y=0(x≥0).过点P(1,0)作直线分别交射线OA,OB于点A,B.

(1)当AB的中点在直线x-2y=0上时,求直线AB的方程;

(2)当∆AOB的面积取最小值时,求直线AB的方程.

(3)当PA·PB取最小值时,求直线AB的方程.

20.(本小题满分16分)已知数列{an}是首项为1,公差为d的等差数列,数列{bn}是首项为1,公比为q(q>1)的等比数列.

(1)若a5=b5,q=3,求数列{anbn}的前n项和;

(2)若存在正整数k(k≥2),使得ak=bk.试比较an与bn的大小,并说明理由.

参考答案

一、填空题

9. x+3y-5=0或x=-1;

13. [-1,+∞)；14.112.

二、解答题

15.(1)因为直线l1:(m-2)x+3y+2m=0,l2:x+my+6=0,直线l1与l2垂直,所以有

(m-2)×1+3m=0,

(2)因为直线l1:(m-2)x+3y+2m=0,l2:x+my+6=0,直线l1与l2平行,所以有

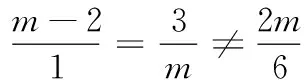
解得m=-1.

16.(1)连结AC、BD.

∵在四棱锥P-ABCD中,ABCD是菱形,PA⊥平面ABCD,∴BD⊥AC,BD⊥PA.

∵PA∩AC=A,∴BD⊥平面PAC.

∵PC⊂平面PAC,∴BD⊥PC.

(2)∵BC∥AD,BC⊄面PAD,AD⊂面PAD,

∴BC∥面PAD.

∵平面PBC与平面PAD的交线为l,

∴BC∥l.

17.(1)设等比数列{an}的公比为q,依题意，

有2a1+a1q2=3a1q,解得q=1或q=2.

∵a3+2是a2,a4的等差中项,

∴2a3+4=a2+a4,

即2a1q2+4=a1q+a1q3.

当q=1时,不成立,

当q=2时,a1=2,

∴an=2n.

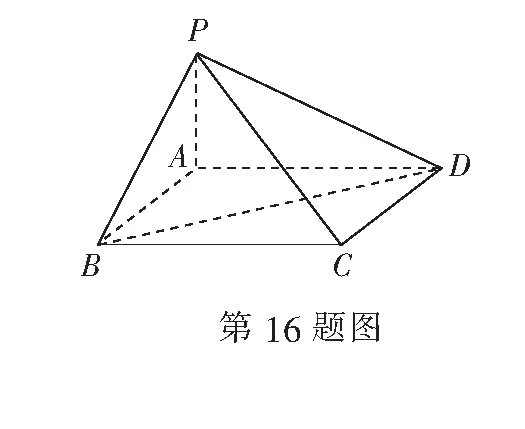
∴Sn=b1+b2+…+bn

-(1+2+3+…+n)

∵Sn+35<0,

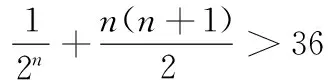
∴n(n+1)≥72,

解得n≥8,

∴使Sn+35<0成立的n的最小值是8.

18. (1)∵折后A,B,C,D重合于一点O,

∴拼接成底面EFGH的四个直角三角形必为全等的等腰直角三角形,

∴底面EFGH是正方形,故EG⊥FH.

∵EFGH是正方形,故EG⊥FH.

∵等腰三角形∆SEE′≌∆SGG′,

∴SE=SG,∴EG⊥SO.

∵SO、FH⊂平面SFH,SO∩FH=O,

∴EG⊥平面SFH.

又∵EG⊂平面SEC,

∴平面SEG⊥平面SFH.

(2)∵AE=BE′=x(cm)，

∴EE′=20-2x,由EE′>0得0

则∆SEE′的高为20,礼品袋的侧面积

S=20×20-4(S∆EAH′+S∆SEE′)

=400-(2x2+400-40x)

=-2x2+40x.

由S=-2x2+40x≥128，得

x2-20x+64≤0,4≤x≤16,

∵0

(3)当x=5时,OE=OF=AE=5,则EF=5,包装盒的内径最小值,即为正四棱锥S-EFGH的外接球的半径R.

设正四棱锥的外接球的球心为O′,则O′在正四棱锥S-EFGH的高SO上.

连结EO′,则Rt∆SEO中,SO=10,

∴O′E=R,O′O=10-R.

Rt∆EOO′中,OE2+O′O2=O′E2,

∴52+(10-R)2=R2,

即25+100-20R=0,

即包装盒的内径R的最小值是6.25.

分别化为a=5b,a+2b-3ab=0，

即7x-4y-7=0.

(2)设A(a,a),B(b,-2b)(a,b>0).

a=b=1时,A(1,1),B(1,-2),

a、b≠1时，

(3)设直线AB的方程为

=f(m),

m=-3时，f(-3)=1.

令m+3=k≠0,

k<0时，

k>0时，

20.(1)依题意,

a5=b5=b1q5-1=1×34=81,

所以an=1+20(n-1)=20n-19.

令Sn=1×1+21×3+41×32+…

+(20n-19)·3n-1,

①

则3Sn=1×3+21×32+…

+(20n-39)·3n-1

+(20n-19)·3n.

②

①-②，得

-2Sn=1+20×(3+32+…+3n-1)

-(20n-19)·3n

-(20n-19)·3n

=(29-20n)·3n-29,

(2)因为ak=bk,所以

1+(k-1)d=qk-1,

又bn=qn-1,

-(n-1)(qk-1-1)]

-(n-1)(qk-2+qk-3+…+q+1)].

(i)当11，知

+…+q+1)

-(n-1)(qk-2+qk-3+…+qn-1)]

-(n-1)(k-n)qn-1]

(ii)当n>k时，由q>1，知

+…+qk-1)

-(n-k)(qk-2+qk-3+…+q+1)]

-(n-k)(k-1)qk-2]

=(q-1)2qk-2(n-k)>0.

综上所述，当1bn;当n>k时，an